Задача
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» - символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос |
Найдено страниц (в тысячах) |
| протон & фотон & бозон |
80 |
| протон & бозон |
240 |
| (протон | фотон) & бозон |
440 |
Компьютер печатает количество страниц (в тысячах), которое будет найдено по следующему запросу:
фотон & бозон
Укажите целое число, которое напечатает компьютер.
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение
Нарисуем круги Эйлера и обозначим все области числами
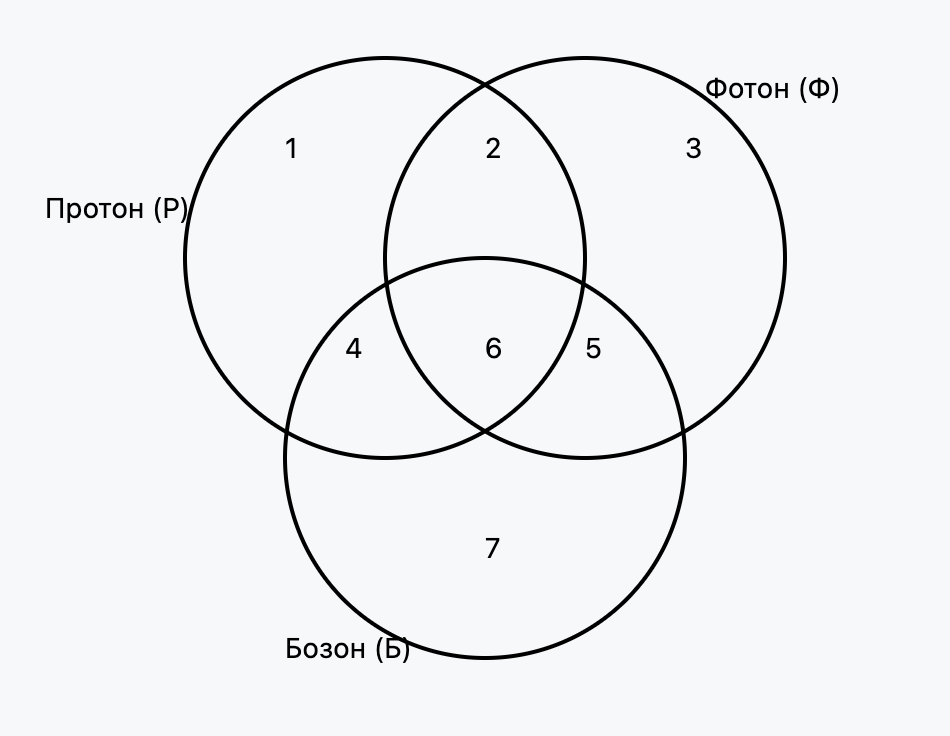 |
Обозначения областей:
1: Только Протон (P)
2: Протон И Фотон (без Бозона)
3: Только Фотон (Ф)
4: Протон И Бозон (без Фотона)
5: Фотон И Бозон (без Протона)
6: Протон И Фотон И Бозон (ПP & Ф & Б) = 80
7: Только Бозон (Б)
|
Шаг 1. Найдем область 4 (Протон & Бозон без Фотона):
Из условия протон & бозон = 240, что включает:
- Область 4 (P & Б без Ф)
- Область 6 (P & Ф & Б) = 80
Область4 = 240 - 80 = 160
Шаг 2. Разберем условие (протон | фотон) & бозон = 440:
Это объединение всех областей, где есть Бозон и (Протон или Фотон):
- Область 4 (P & Б без Ф) = 160
- Область 5 (Ф & Б без P) = ?
- Область 6 (P & Ф & Б) = 80
Уравнение:
160 (Обл.4) + x (Обл.5) + 80 (Обл.6) = 440
x = 440 - 160 - 80 = 200
Шаг 3. Находим искомое фотон & бозон:
Это сумма:
- Область 5 (Ф & Б без P) = 200
- Область 6 (P & Ф & Б) = 80
Ф & Б = 200 + 80 = 280
Ответ: 280 (тысяч страниц)