| Разбор 1 "Задача о размене" |
| Задача 1. а) Можно ли разменять 25 рублей при помощи десяти купюр достоинством в 1, 3 и 5 рублей?
б) Можно ли разменять 70 рублей при помощи десяти купюр достоинством в 2, 10 и 14 рублей?
|
|
| Разбор 2 "Задача о тетради" |
| Задача 2. Петя купил тетрадь объёмом 96 листов и пронумеровал все её страницы по порядку числами от 1 до 192. Вася вырвал из этой тетради 25 листов и сложил все 5050 чисел, которые написаны на них. Могло ли у него получиться 1000? |
|
| Разбор 3 "Задача о пяти числах" |
| Задача 3. Даны пять целых чисел. Сумма любых трёх из них чётна. Докажите, что все числа чётны. |
|
| Разбор 4 "Задача о числах на круге" |
| Задача 4. По кругу выписано 101 натуральное число. Докажите, что найдутся два соседних числа такие, что после их выкидывания оставшиеся числа нельзя разбить на две группы с равной суммой. |
|
| Разбор 5 "Задача о Черноморе" |
| Задача 5. Дядька Черномор написал на листке бумаги число 20. Затем он отдал листок одному из тридцати трёх богатырей. Каждый богатырь, получив листок, меняет написанное на нём число на 1 (прибавляет или отнимает), после чего передаёт листок следующему богатырю. Листок побывал у каждого богатыря по одному разу. Могло ли в результате получиться число 10? |
|
| Разбор 6 "Задача о шахматном короле" |
|
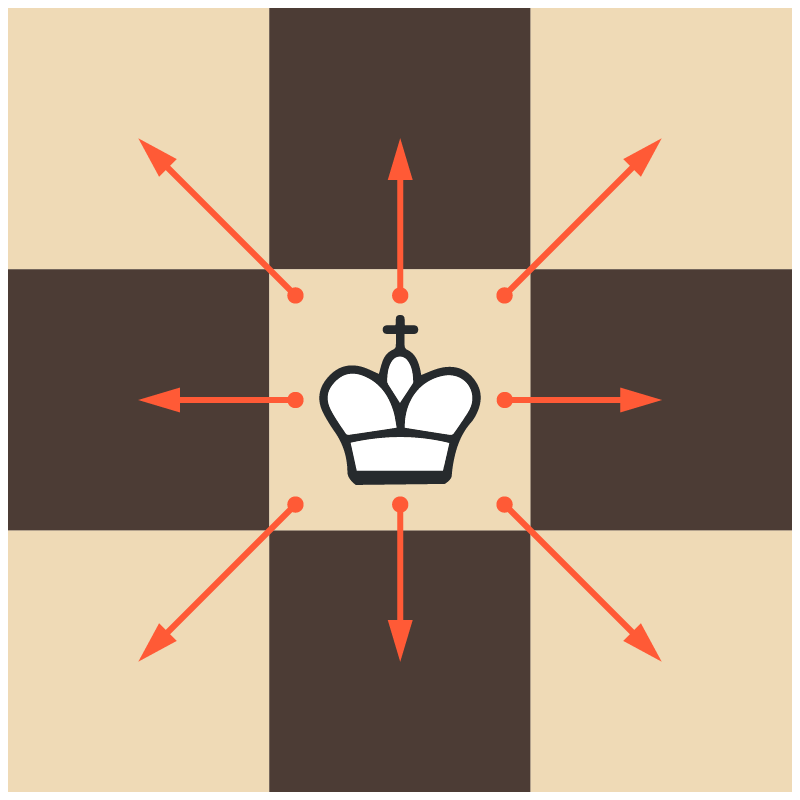
Задача 6. Шахматный король обошёл шахматную доску 8×8, побывав в каждой клетке один раз, и вернулся в первоначальную клетку. Докажите, что он сделал чётное число ходов по диагонали.
Король ходит в одну из восьми соседних клеток.
|
|
| Разбор 7 "Задача о цифрах" |
| Задача 7. Можно ли выписать в ряд по одному разу цифры от 1 до 9 так, чтобы между единицей и двойкой, двойкой и тройкой, ……, восьмёркой и девяткой было нечётное число цифр? |
|
| Разбор 8 "Задача о точках на круге" |
|
Задача 8. По кругу отмечена 101 точка одного из двух цветов.
а) Докажите, что найдутся две одноцветные точки, идущие подряд.
б) Докажите, что найдутся две одноцветные точки, между которыми находятся ровно две другие точки.
|
|
| Разбор 9 "Задача о 99 карточках" |
| Задача 9. На 99 карточках пишутся числа 1, 2, 3, ……, 99. Затем карточки перемешиваются, раскладываются чистыми сторонами вверх и на чистых сторонах снова пишутся числа 1, 2, 3, ……, 99. Для каждой карточки числа, написанные на ней, складываются, и 99 полученных сумм перемножаются. Докажите, что в результате получится чётное число |
|
| Разбор 10 "Задача о представлении 1" |
| Задача 10. Можно ли представить 1 в виде суммы ста дробей вида 1/n, где n — нечётное натуральное число? |
|