Статья Автор: Лебедев Дмитрий

Конспект _Оценка + Пример


Комби-7 Оцннка + Пример Часть 1  

Задачи, в которых требуется найти наименьшее или наибольшее возможное значение некоторой величины, предполагают решение, состоящее из двух независимых частей: приведение оптимальной конструкции (обычно её называют «пример») и доказательство, что конструкция действительно оптимальна (обычно её называют «оценка»).

Задача. Найдите наибольшее натуральное число, состоящее из различных цифр, в котором любые две подряд идущие цифры образуют двузначное число, делящееся на 3.

Задача. В стране есть монеты номиналами 1, 4, 5, 20 и 100 рублей. Каким наименьшим количеством монет можно набрать сумму в 348 рублей?

Жадный алгоритм — это алгоритм, в котором на каждом шаге делается оптимальный на данный момент выбор. Жадный алгоритм бывает полезен при построении примера, хотя и не всегда приводит к правильному ответу.

Комби-7 Оценка + Пример. Часть 2. Разбиение на части

В задачах на клетчатой доске при доказательстве оценки часто помогает идея разбиения всей доски на более мелкие части и доказательства оценки в них.

Задача. Какое наибольшее количество ладей можно поставить на доску 8×8 так, чтобы никакие две ладьи не били друг друга?

Задача. На доску 10×10 для игры в морской бой поставили корабль 1×4. Какое наименьшее число выстрелов надо сделать, чтобы гарантированно его подбить?

Пусть в задаче требуется минимизировать некоторую величину. Типичной ошибкой при доказательстве оценки является следующее рассуждение: «Если из приведённого примера нельзя ничего убрать так, чтобы условие задачи не нарушилось, то такой пример — оптимальный.»

Вывод в этом рассуждении неверен. Приведённый пример нельзя улучшить, убрав из него что-то, но из этого не следует, что пример нельзя улучшить как-нибудь иначе.

Комби-7 Оценка + Пример. Часть 3 Подсчёты

Задача. У Пети есть n корзинок с яблоками. В первой корзинке 1 яблоко, во второй — 2, в третьей — 3 и т. д. Он хочет раздать корзинки девятерым своим друзьям так, чтобы у каждого оказалось хотя бы по 9 яблок. При каком наименьшем n он сможет это сделать?

Оценка, как правило, является более сложной частью задачи, чем пример. Однако иногда сначала полезно сделать оценку, чтобы получить информацию, необходимую для построения примера.

Задача. В клетчатой таблице 5 строк и несколько столбцов. В каждую клетку таблицы поставили число 0, 1 или 2 так, что суммы чисел во всех строках одинаковы, а во всех столбцах различны. Какое наибольшее количество столбцов может быть в таблице?

Задачи для тренировки

1) 7_12_1 Есть девять коробок, в них лежат

  
2)  7_12_2 Есть восемь коробок, в них лежат  
3) 7_12_3 Грабители хотят унести из мясного магазина   
4) 7_12_4 Найдите наибольшее натуральное число  
5) 7_12_5 Какое наименьшее число выстрелов   
6) 7_12_6 Дан белый клетчатый квадрат   
7) 7_12_7 Какое наибольшее число ферзей можно  
8) 7_12_8 Какое наибольшее количество пешек можно <???>  
9) 7_12_9 Приведите пример к предыдущей задаче <???>  
10) 7_12_10 Влад нарисовал клетчатый многоугольник  
11) 7_12_11 Какое наименьшее количество клеток изначально  
12) 7_12_12 В некоторых клетках доски  

Задачи с разбором

Разбор 1а "Задача о расстановке королей"

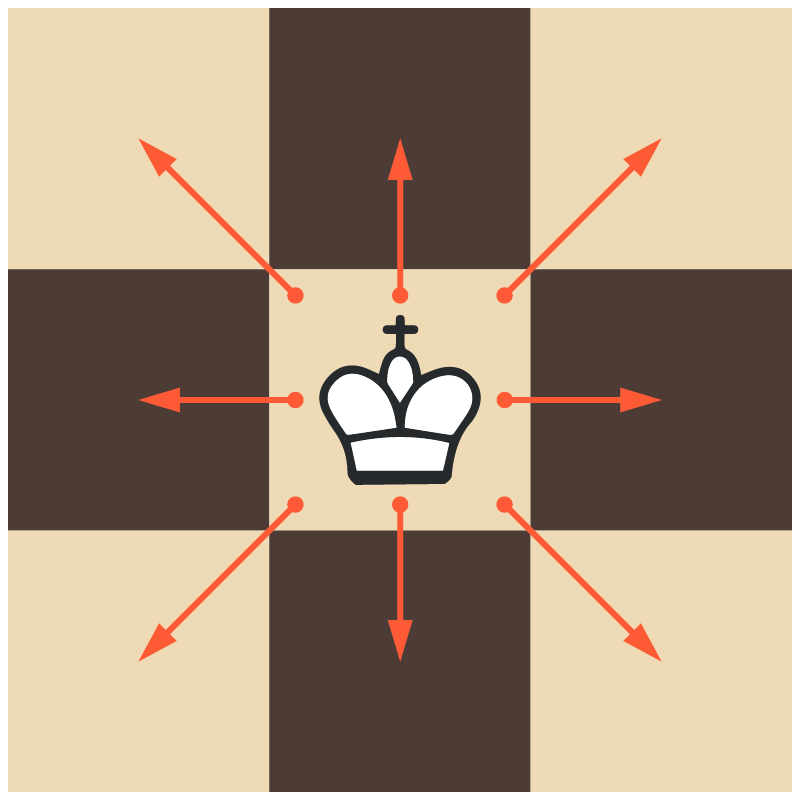
Задача 1a. Какое наибольшее количество королей можно расставить на шахматной доске так, чтобы они не били друг друга?

Напоминание. Король ходит в одну из восьми соседних клеток.

  
Разбор 1b "Задача о расстановке королей на поле без углов"

Задача 1b. Из шахматной доски вырезали 4 угловые клетки. Какое наибольшее количество не бьющих друг друга королей можно поставить на оставшиеся клетки шахматной доски?

  
Разбор 2 "Задача о расстановке слонов"

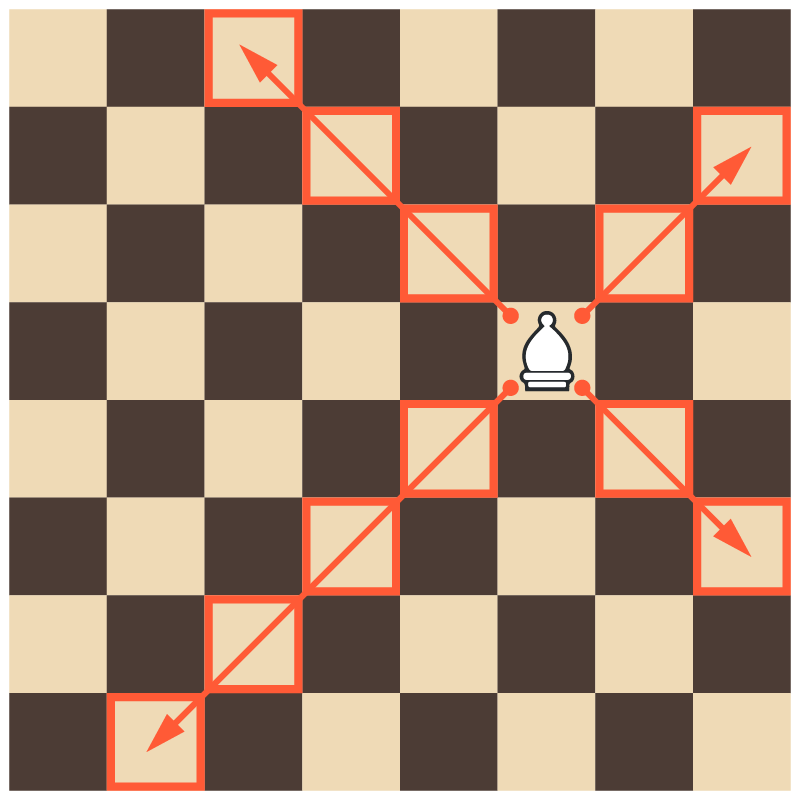
Задача 2. Какое наибольшее количество слонов можно расставить на шахматной доске так, чтобы они не били друг друга?

Напоминание. Слон ходит на любое количество клеток по диагонали.

  
Разбор 3 "Задача о расстановке коней"

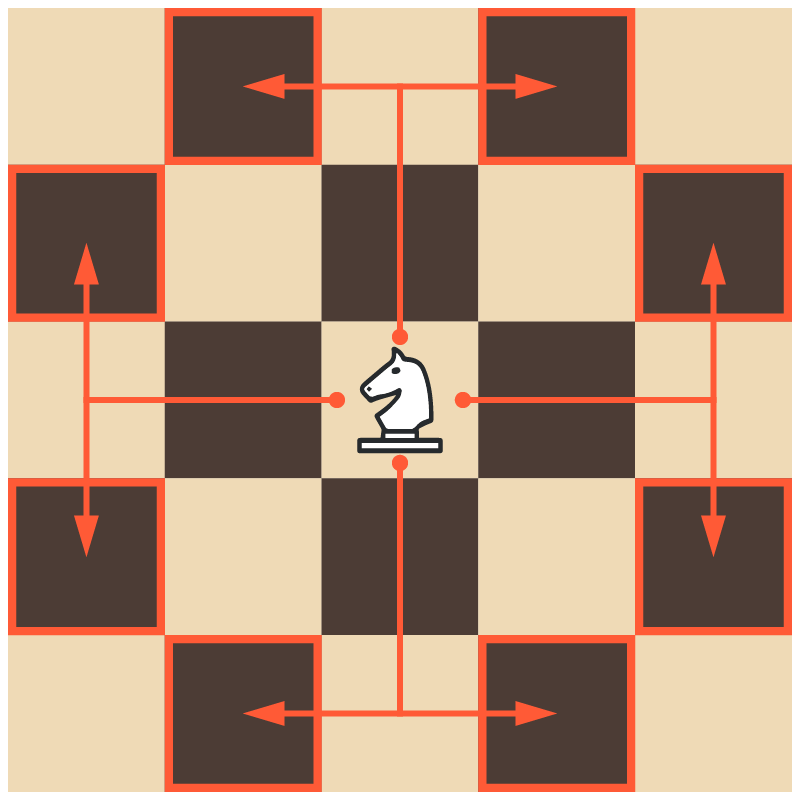
Задача 3. Какое наибольшее количество коней можно расставить на шахматной доске так, чтобы они не били друг друга?

Напоминание. Конь ходит на две клетки в некотором направлении и на одну клетку в перпендикулярном ему направлении.

  
Разбор 4 "Задача о Белоснежке"
Задача 4. Белоснежка вошла в комнату, где вокруг круглого стола стояло 30 стульев. На некоторых стульях сидели гномы. Оказалось, что Белоснежка не может сесть так, чтобы рядом с ней никто не сидел. Какое наименьшее число гномов могло быть за столом?  
Разбор 5 "Задача о расстановке прямоугольников"
Задача 5. Для какого наименьшего nn на доске 10×10 можно расставить прямоугольники 1×1, 1×2,…,1×n (возможно, повёрнутые на 90∘) так, чтобы на доске не осталось места для прямоугольника 1×(n+1)?  
Разбор 6 "Задача о расстановке ладей "
Задача 6. На доске 30×n расставлено несколько ладей таким образом, что каждая ладья бьёт ровно одну ладью. При этом в каждой вертикали и в каждой горизонтали стоит хотя бы одна ладья. При каком наибольшем nn такое возможно? При каком наименьшем nn такое возможно?  
Разбор 7 "Задача про фрукты"
Задача 7. В ряд выложены апельсины, бананы, яблоки и груши так, что все четыре вида фруктов представлены, и представители любых двух видов где-то лежат рядом. Какое наименьшее количество фруктов могло быть выложено?  
Разбор 8 "Задача про 0 и 1 в прямоугольнике"
Задача 8. В каждую клетку прямоугольника 10×19 записали одно из чисел 0 или 1, после чего подсчитали суммы чисел в каждой строке и в каждом столбце. Какое наибольшее количество различных чисел могло получиться?  
Разбор 9 "Задача про числа на окружности"
Задача 9. По окружности написано 10 натуральных чисел, сумма которых равна 100. Известно, что сумма любых трёх подряд идущих чисел не меньше 29. Какое максимальное значение может принимать максимальное из этих чисел?  
Разбор 10 "Задача про лотерею "
Задача 10. В лотерее 39 шаров, пронумерованных числами от 1 до 39. Играющий заполняет карточку, где указывает шесть номеров. В розыгрыше лотереи номера шести шаров объявляются неудачными. Игрок выиграет, если на его карточке нет ни одного неудачного числа. Какое наименьшее количество карточек можно заполнить так, чтобы гарантированно победить?  
Разбор 11 "Задача про детей в круге"
Задача 11. По кругу стоят 15 детей: мальчики и девочки. Известно, что справа от каждого мальчика стоит ребёнок в синей футболке, а слева — ребёнок в красной футболке. Какое наибольшее количество мальчиков может быть среди этих детей?  
Разбор 12 "Задача о дисквалификации спортсменов"
Задача 12. Сто спортсменов на соревнованиях заняли места с первого по сотое. После того, как некоторых из них дисквалифицировали, места всех остальных изменились на разные числа (возможно, на 0). Какое наименьшее количество спортсменов могло быть дисквалифицировано?  
Разбор 13 "Задача про пещеру с мешками "
Задача 13. В пещере лежат в ряд 100 мешков. В каждом мешке находится золото или серебро, масса каждого мешка 1 кг и 2 кг. Рядом с каждым двухкилограммовым мешком лежат два мешка с серебром, а рядом с каждым килограммовым — хотя бы один мешок с серебром. Али-Баба унёс из пещеры всё золото. Какое наибольшее количество золота ему могло достаться?  

Печать