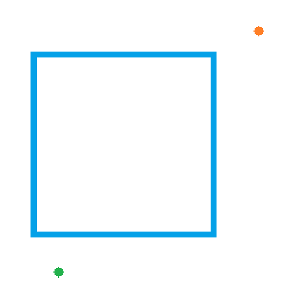
Саша и Маша живут в разных домах одного района. Их дома находятся возле пруда в форме квадрата. Однажды глава района предложил жителям нарисовать тропинки, которые они хотели бы видеть в своём районе, чтобы в дальнейшем проложить их. Потому ребята решили рассчитать самый короткий маршрут, который может быть, чтобы пройти от одного дома к другому. На изображении ниже представлен вариант расположения пруда и двух домов ребят (зелёная точка и оранжевая). Требуется рассчитать, какое самое кратчайшее расстояние требуется им преодолеть, чтобы оказаться друг у друга в гостях.
 Примечание
Примечание:
- дома могут находиться как по разные стороны пруда, так и поодну;
- требуется рассчитать ответ с точностью до десятых (если ответполучился целый, то выводить всегда после запятой один знак);
- передвигаться можно только по прямым, но не дугам;
- стороны пруда всегда параллельны осям OX и OY;
- точки, обозначающие дома могут лежать на границе пруда, и передвигать по границе пруда разрешено.
Формат входных данных
На первой строке подаются параметры пруда через пробел a, x1, y1 (1 <= a <= 1000; -1000 <= x1,y1 <= 1000), где x1,y1 – координаты левого верхнего угла пруда.
На второй строке подаются координаты дома Маши в виде точки xm, ym (-1000 <= xm, ym <= 1000).
На третьей строке подаются координаты дома Саши в виде точки xs, ys (-1000 <= xs, ys <= 1000).
Все числа - целые.
Формат выходных данных
Выведите на одной строке самое кратчайшее расстояние, которое можно пройти от дома Маши к дому Саши. Ответ представляет собой всегда вещественное число с одним знаком после запятой. Если ответ получился больше, то округлить до одного знака после запятой (было 4.5764, стало 4.6).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
2 2 4
1 1
5 3
|
4.6
|
|
2
|
2 2 4
1 1
5 1
|
4.0
|