Законы логики
Закон двойного отрицания: \(\neg(\neg A) \equiv A\)
Законы де Моргана:
- \(\neg(A \land B) \equiv \neg A \lor \neg B\)
- \(\neg(A \lor B) \equiv \neg A \land \neg B\)
Дистрибутивные законы:
- \(A \land (B \lor C) \equiv (A \land B) \lor (A \land C)\)
- \(A \lor (B \land C) \equiv (A \lor B) \land (A \lor C)\)
Закон исключения третьего: \(A \lor \neg A \equiv 1\)
Закон противоречия: \(A \land \neg A \equiv 0\)
Закон повторения: \(A \land A \equiv 1 \\ A \lor A \equiv 1 \\ \)
Закон поглощения: \(A \lor A \land B \equiv A \\ \)
Преобразование импликации
Импликация может быть преобразована в дизъюнкцию:
\(A \rightarrow B \equiv \neg A \lor B\)
Отрицание импликации:
\(\neg(A \rightarrow B) \equiv A \land \neg B\)
Примеры типовых задач
Задача 1: На числовой прямой даны два отрезка: P = [10, 20] и Q = [30, 50]. Укажите наибольшую возможную длину отрезка A, для которого формула
\((x \in A) \rightarrow ((x \in P) \lor (x \in Q))\)
тождественно истинна.
Решение:
1. Обозначим: \((x \in A) = A \\ (x \in P) = P \\ (x \in Q) = Q\)
2. Перепишем выражение и упростим: \(\neg A \lor P \lor Q\)
3. Выражение ложно только когда A истинно, а P и Q ложны
4. Нарисуем на числовой оси данные области
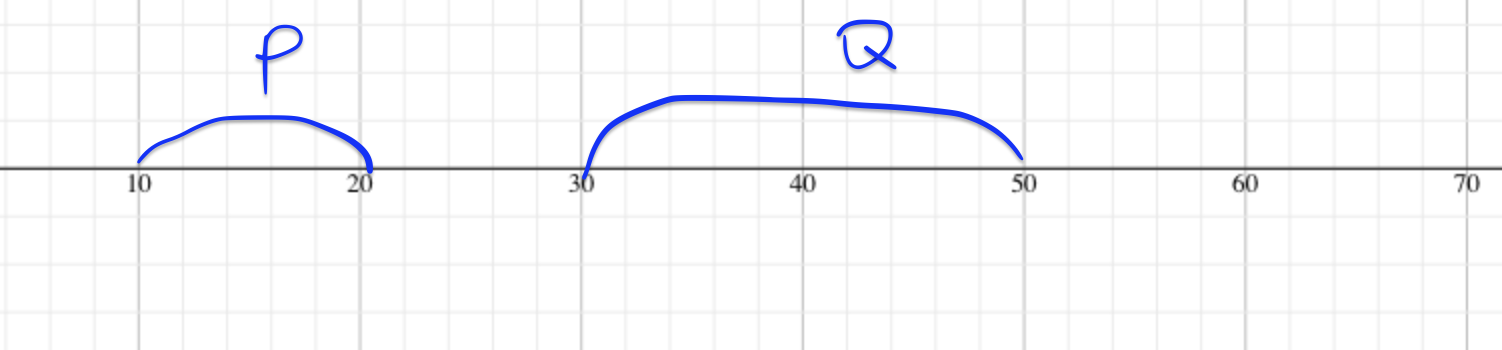
5. Чтобы формула была тождественно истинной, выражение не должно быть ложным ни при каком x. Если x попадает в одну из областей \((-\infty, 10), (20, 30), (50, +\infty)\) выражение \( P \lor Q\) станет ложным. Следовательно, \(\neg A\) должно быть в этот момент истинным.
6. Значит, отрезок A не должен содержать точек из \((-\infty, 10) \cup (20, 30) \cup (50, +\infty)\).
7. Отрезок A может содержать только точки из [ 10 , 20 ] или [ 30 , 50 ]. Наибольший непрерывный отрезок, который можно выбрать, — это отрезок A=[30,50]
8. Длина наибольшего отрезка\( 50-30 = 20\)
9. Ответ: 20
Задача 2: Элементами множества А являются натуральные числа. Известно, что выражение
¬(x ∈ A) → (¬(x ∈ {1, 12}) ∧ ¬(x ∈ {12, 13, 14, 15, 16}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное количество элементов множества A.
Решение:
1. Обозначим:
-
P = (x ∈ {1,12})
-
Q = (x ∈ {12,13,14,15,16})
2. Упростим: ¬A → (¬P ∧ ¬Q) ≡ A ∨ (¬P ∧ ¬Q)
3. Выражение должно быть тождественно истинным (то есть истинно при всех натуральных x).
4. Если (¬P ∧ ¬Q) - ложно, то А - должно быть обязательно истинным.
5. Значит минимальное А должно быть \(\neg (\neg P \land \neg Q) = P \lor Q\)
6. Следовательно: \(A_{min} = P \lor Q\). Другими словами, минимальное множество А это объединение множеств P и Q. \(A_{min} ∈ \{1, 12, 13, 14, 15, 16\}\) - множество А содержит 6 элементов
7. Ответ: 6