В сказочном мире Геомаба живут необычные существа в виде прямоугольников. Все они разного размера, но передвигаются все они одинаково –перекатыванием сбоку на бок. В очередной из дней жители Геомаба решиливыбрать себе мэра, так как дороги в их мире очень опасные – в них очень многоям и в них легко застрять, так как жители-прямоугольники могут передвигатьсятолько по плоским дорогам.
Мэр решил незамедлительно собрать группу добровольцев и направить их по дорогам Геомаба, но дорог так много, что Мэр понял, что отправлять добровольцев, а потом вытаскивать их из ям – дело трудозатратное, потому он обратился к Вам за помощью – написать алгоритм, который по размеру прямоугольника покажет все ямы, которые необходимо залатать, чтобы житель-прямоугольник смог спокойно передвигаться по дороге, а город потратил минимально ресурсов (заделал как можно меньше ям).
Прямоугольник считается застрявшим, если он не смог беспрепятственно перекатиться через яму (его угол попал в яму (не включая начало и конец ямы)).
Если прямоугольник попал не углом в яму, а попал точно стороной на границы ямы, то он не считается застрявшим.
Формат входных данных
На вход на первой строке подаётся число X (1 <= X <= 100000) – длина дороги в метрах.
На второй строке подаются числа W, H (1 <= W,H <= 100) – высота и ширина жителя-прямоугольника в метрах соответственно.
На третьей строке подаётся число N (1 <= N <= 1000) – количество ям на дороге.
Далее на N-строках подаются координаты начала ямы (в метрах от начала дороги) и её ширина в виде целых положительных чисел от 1 до X. Координаты ям могут подаваться в любом порядке. Но все ямы не пересекаются и не накладываются.
Формат выходных данных
Выведите на первой строке количество ям, которые необходимо заделать, чтобы житель-прямоугольник, для которого производится расчёт, смог добраться до конца дороги.
Далее выведите координаты всех ям отсортированные в порядке появления от начала дороги до конца, КАЖДУЮ С НОВОЙ СТРОКИ.
Примечание
Житель-прямоугольник перед стартом дороги находится так, что три его вершины находятся за пределом начала дороги, а одна вершина, являющаяся самой правой, стоит на позиции 0. Первоначальное положение жителя-прямоугольника может быть любым, нужно выбрать оптимальное, чтобы залатать как можно меньше ям.
Если решений несколько, выведите то, в котором сумма координат ям для залатывания наименьшая.
В данном случае житель может стоять основанием перед началом дороги на стороне 2 (положение №1) или 3 (положение №2).
Если он стоит на основании длиной 2, то он попадёт только в яму под номером 14.
Если он стоит на основании длиной 3, то он попадёт в ямы 10 и 14.
Городу выгоднее заделать только одну яму, под номером 14.
Положение №1.
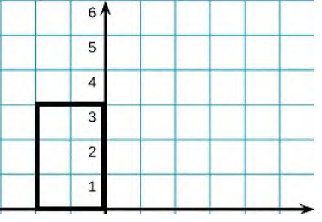
Положение №2.
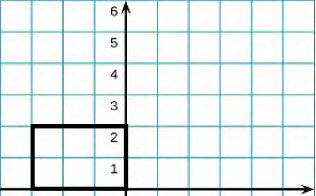
Примеры
| № | Входные данные | Выходные данные |
|
1
|
50
3 2
3
10 3
14 2
20 1
|
1
14
|