Город имеет форму прямоугольника с вершинами в точках (-W,-H), (-W,H), (W,H),(W,-H).
Плоскость разбита на кварталы. Квартал — это единичная клетка, вершины которой имеют целочисленные координаты. Назовем квартал городским, если все вершины квартала находятся внутри города (считается, что точка на границе принадлежит городу). Всего в городе будет 4·W·H кварталов.
Дорожная сеть состоит из N дорог (часть дорог или все проходят через город).
Дорога — это прямая линия, не параллельная осям координат.
Дорога задается двумя различными точками на ней (точки могут находиться вне города).
Для каждого квартала определим "
значимость".
Значимость квартала равна количеству дорог, проходящих через этот квартал. Считается, что дорога проходит через квартал, если имеет с кварталом не менее двух общих точек.
Найдите значение "значимости" для каждого квартала. Для каждой полученной "значимости" определите количество кварталов, имеющих эту значимость.
Формат входных данных
В первой строке заданы значения W, H, N (9<W,H<201, 0<N<1001)
В следующих N строках задано по четыре числа (координаты двух точек прямой, определяющих дорогу).
Формат выходных данных
В первой строке выведите число K - количество различных ненулевых значений "значимости".
В следующих K строках выведите по два числа - значение "значимости" и количество кварталов, имеющих такое значение "значимости".
Примечание к примеру
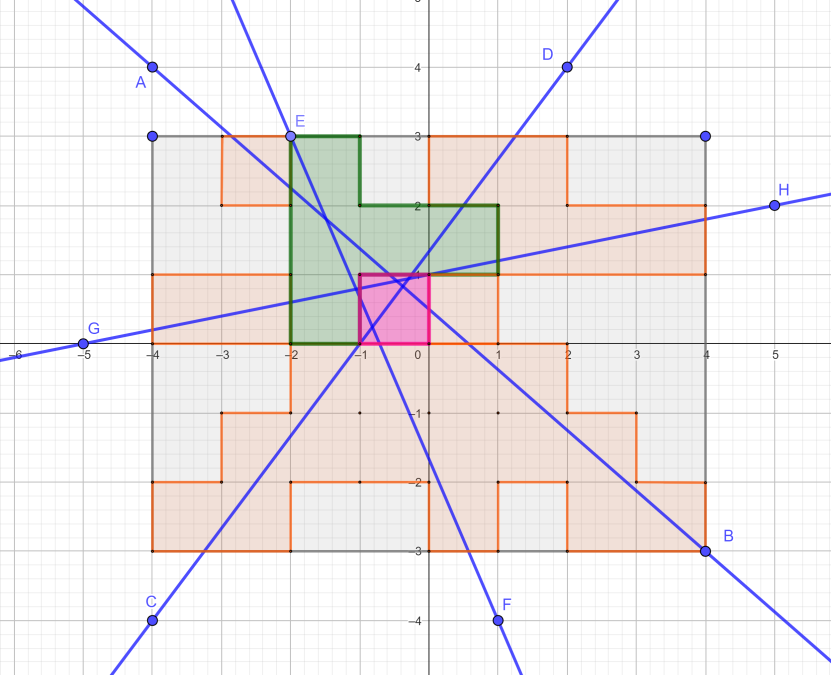
Город расположен в прямоугольнике со сторонами 8 и 6 клеток (всего 48 кварталов)
Через город проходят 4 дороги AB, CD, EF, GH
Значимость 1 будет у 24 кварталов (коричневый цвет на рисунке)
Значимость 2 будет у 5 кварталов (зеленый цвет на рисунке)
Значимость 4 будет у 1 кварталов (красный цвет на рисунке)
18 кварталов будут иметь значимость равную 0 (на печать не выводиться)
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4 3 4
-4 4 4 -3
-4 -4 2 4
-2 3 1 -4
-5 0 5 2
|
3
1 24
2 5
4 1
|