Задача
Логическая функция F задаётся выражением:
(x ∨ y) ∧ ¬(y ≡ z) ∧ ¬w
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки:
| ? |
? |
? |
? |
F |
| 1 |
|
1 |
|
1 |
| 0 |
1 |
|
0 |
1 |
| |
1 |
1 |
0 |
1 |
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Решение в электронных таблицах (построение таблицы истинности в электронных таблицах)
- Поскольку во время компьютерного экзамена есть возможность использовать электронные таблицы, можно построить таблицу истинности с их помощью
- Заполняем первую часть таблицы, перечисляя все комбинации переменных в порядке возрастания двоичного кода:
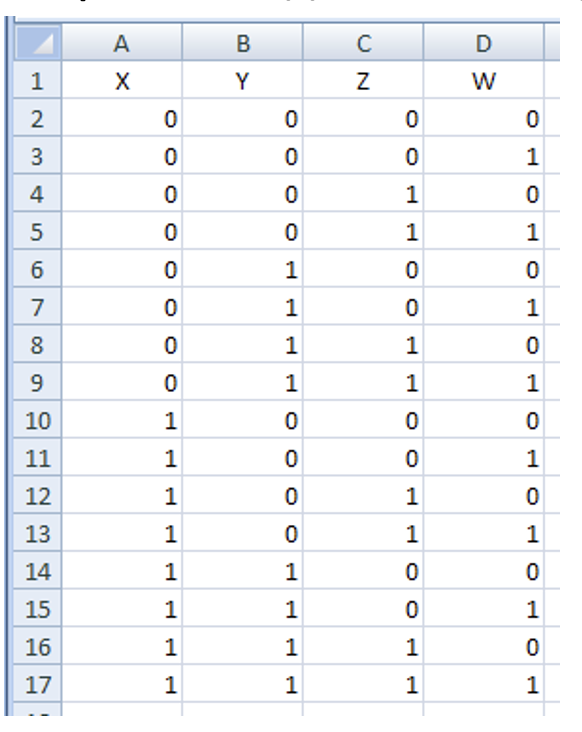
- Для каждой строчки определяем выражения, входящие в логическое произведение, а затем - значение функции (столбцы E, F, G, H)
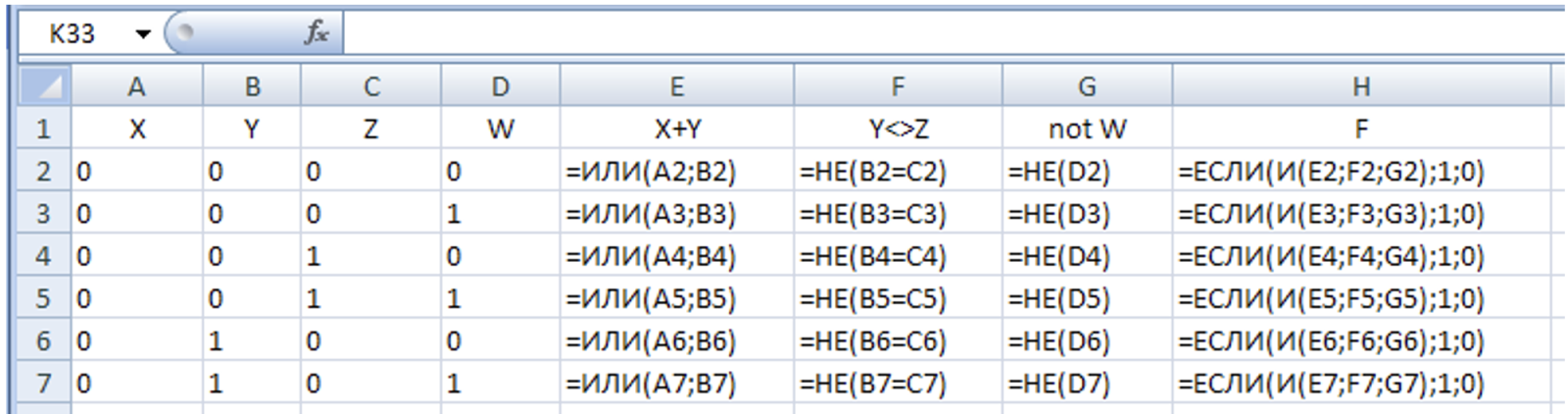
- Сортируем строки таблицы по столбцу H по убыванию:
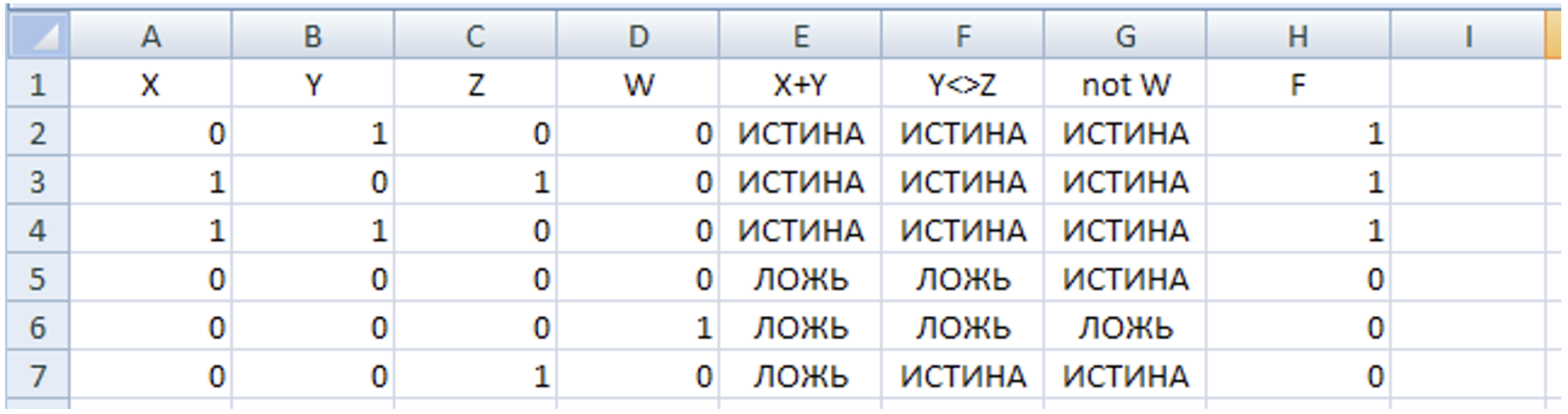
- Удаляем строки, где функция равна 0; можно также скрыть вспомогательные столбцы E, F, G:
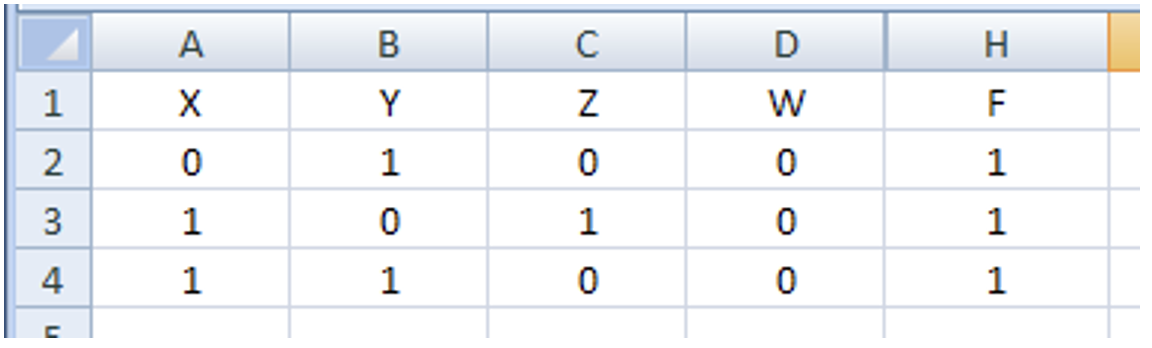
- Дальше рассуждаем так же, как и при теоретическом решении, сопоставляя с исходной таблицей:
- Ответ: \(\boxed{zyxw}\)