Задание
По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж и З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| А |
00 |
| Б |
1000 |
| В |
101 |
| Г |
1001 |
| Д |
01 |
| Е |
110 |
Какое
наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв?
В ответе запишите суммарную длину кодовых слов для букв: Ж, З.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова.
Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Принципы построения кодов
- Постройте дерево кодирования (аналог дерева Хаффмана) для визуализации (двоичное дерево, где от каждого узла отходит две ветки 0 и 1)
- Постройте дерево на основе известных кодов.
- Достраивайте дерево для оставшихся букв, чтобы не нарушать условие Фано (ни одна буква не должна находиться в узле дерева). Чтобы условие Фано не нарушалось, буквы должны располагаться на листьях (то есть от буквы не должны идти другие ветви)
- Если нужно достроить дерево для оставшихся букв и учитывать, что код для последовательности суммарно был наименьшим, в этом случае буквы с большой частотой встречаемости необходимо подвешивать ближе к корню (чтобы код буквы был как можно меньше)
Данный метод решения нагляднен и эффективен. Процесс кодирования становится понятным и удобным даже для сложных задач.
Решение
Для решения построим дерево кодов для кодов известных букв и посмотрим куда можно "подвесить" другие буквы.
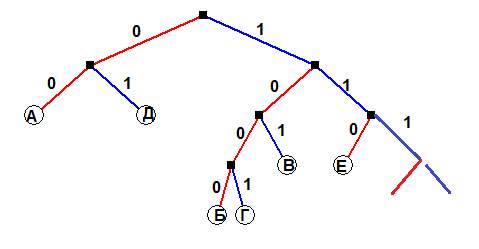
Заметим, что для оставшихся букв доступна ветка, начинающаяся на
111. Следовательно, буквам Ж и З можно дать коды длиной по 4 символа.
Ответ: \(\boxed{8}\)