Задание
Для кодирования некоторой последовательности, состоящей из всех заглавных букв русского алфавита, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известны кодовые слова некоторых букв алфавита: А – 0, Б – 10. Какую наименьшую длину может иметь код подпоследовательности РАЗМЕР?
Решение
Чтобы последовательность РАЗМЕР имела наименьшую длину необходимо буквам, которые встречаются чаще дать минимальный код. в данной последовательности буква Р встречается чаще других. Поэтому, ей необходимо дать по возможности код короче, чем у оставшихся букв.
Построим дерево Фано и достроим его для оставшихся букв, не забывая, что у буквы Р должен быть код с наименьшей длиной (среди букв с неизвестным кодом). Кроме этого необходимо учитывать, что последовательность строится
из всех букв русского алфавита, а не только из тех, которые есть в последовательности РАЗМЕР. Следовательно, необходимо оставить место для "подвешивания" других букв.
Один из вариант дерева имеет следующий вид:
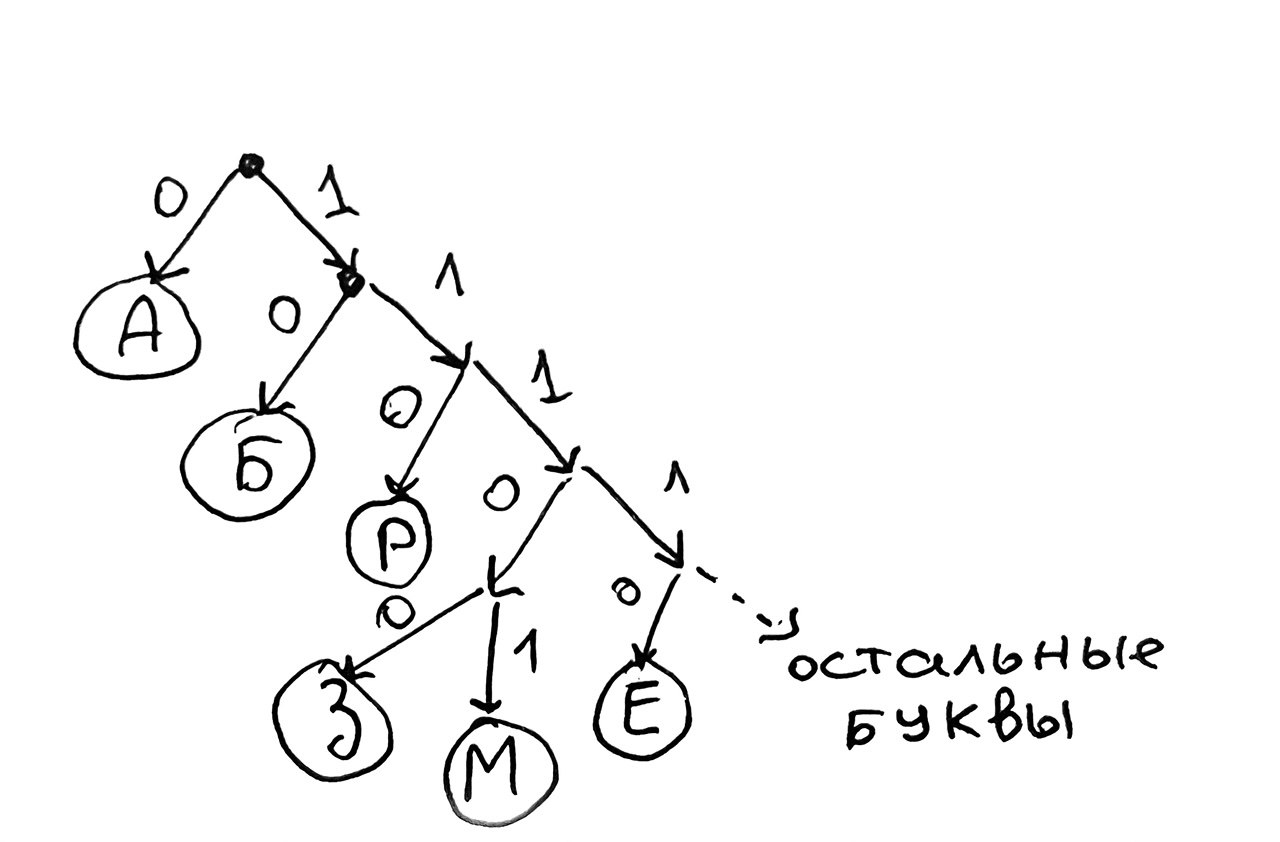
Получаем:
| Буквы |
Длина кода |
| Р |
3 |
| А |
1 |
| З |
5 |
| М |
5 |
| Е |
5 |
Наименьшая длина кода последовательности РАЗМЕР равна 3*2+1+5+5+5 = 22
Ответ:
\(\boxed{22}\)