На самом деле, если граф симметричный, то для решения задачи можно работать с парой вершин.
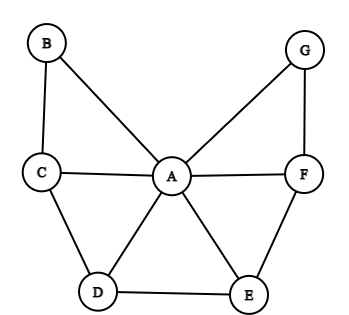
На рисунке схема дорог N-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта C в пункт D и из пункта E в пункт F.
В ответе запишите целое число.
| |
П1 |
П2 |
П3 |
П4 |
П5 |
П6 |
П7 |
| П1 |
х |
27 |
24 |
|
|
|
|
| П2 |
27 |
х |
21 |
|
18 |
|
|
| П3 |
24 |
21 |
х |
15 |
12 |
9 |
30 |
| П4 |
|
|
15 |
х |
|
33 |
|
| П5 |
|
18 |
12 |
|
х |
|
36 |
| П6 |
|
|
9 |
33 |
|
х |
39 |
| П7 |
|
|
30 |
|
36 |
39 |
x |
|
 |
В данной задаче для нахождения ответа достаточно определить сумму двух симметричных ребер: CD и EF. Даже если мы не знаем, какая вершина где именно расположена, сумма длин симметричных рёбер остаётся неизменной.
Значит, ответ можно найти, не уточняя точное положение C, D, E, F — достаточно знать, что CD = EF.
Решите данную задачу и запишите ответ.