Арифметические операции над числами

Мы уже познакомились с целочисленным типом данных и некоторыми операциями над числами. В этом уроке мы рассмотрим все остальные арифметические операции, а также затронем вещественный тип данных, порядок выполнения операций в Python и скобочные выражения.

Основные арифметические операции

В таблице ниже представлены 4 основных математических операции (+, -, *, /), доступных в Python.

Приведённый ниже код:

x = 24
y = 5
print(x + y)
print(x - y)
print(x * y)
print(x / y)

выводит

29
19
120
4.8

Обратите внимание на то, что в результате деления  $24$ на  $5$  получается число $4.8$, содержащее дробную часть.

Тип данных float

Числа с плавающей точкой (они же вещественные) принадлежат в Python к типу float. Эти числа представлены последовательностью десятичных цифр и точкой, являющейся разделителем между целой и дробной частью. 

Примеры вещественных чисел: $\frac{5}{7}$, $\frac{16}{3}$, $4.8$, π.

Приведенный ниже код:

result = 10 / 2
print(result)
print(type(result))

выводит

5.0
<class 'float'>

Отсюда следует важный вывод: при использовании операции деления (/) в  Python результатом всегда будет являться число типа float, причем независимо от того, делится одно число на другое без остатка или нет.

Над вещественными числами, как и над целыми, можно производить различные арифметические операции.

Этот код:

a = 5.0
b = 2.5
print(a + b)
print(a * b)
print(a - b)
print(a / b)

выводит

7.5
12.5
2.5
2.0

При выполнении различных операций с числами типа float на выходе всегда получается число того же типа.

Примечание. С помощью функции int() можно преобразовать вещественное число к целочисленному типу — в этом случае дробная часть будет отброшена. Например, int(52.6) вернёт $52$.

Дополнительные арифметические операции

Существует также 3 дополнительных операции (//, %, **), расширяющих спектр возможностей при работе с числами.

Целочисленное деление

Оператор целочисленного деления (//) отличается от обычного оператора деления (/) тем, что он округляет получившийся результат до ближайшего меньшего целого числа.

Приведенный ниже код:

print(15 // 2)
print(10 // 2)
print(3 // 7)
print(235 // 10)

выводит

7
5
0
23

В примерах выше мы работали с положительными числами. При целочисленном делении отрицательных чисел округление тоже осуществляется до ближайшего меньшего целого, а потому -8 // 3 вернёт $-3$.

Данный код:

print(-10 // 4)
print(-10 // -3)
print(15 // -6)
print(20 // -3)

выводит

-3
3
-3
-7

Деление с остатком

Оператор деления с остатком (%) возвращает остаток от деления одного числа на другое. Если число делится нацело, тогда возвращается ноль. 

Приведенный ниже код:

print(5 % 3)
print(10 % 6)
print(4 % 2)
print(22 % 10)

выводит

2
4
0
2

 

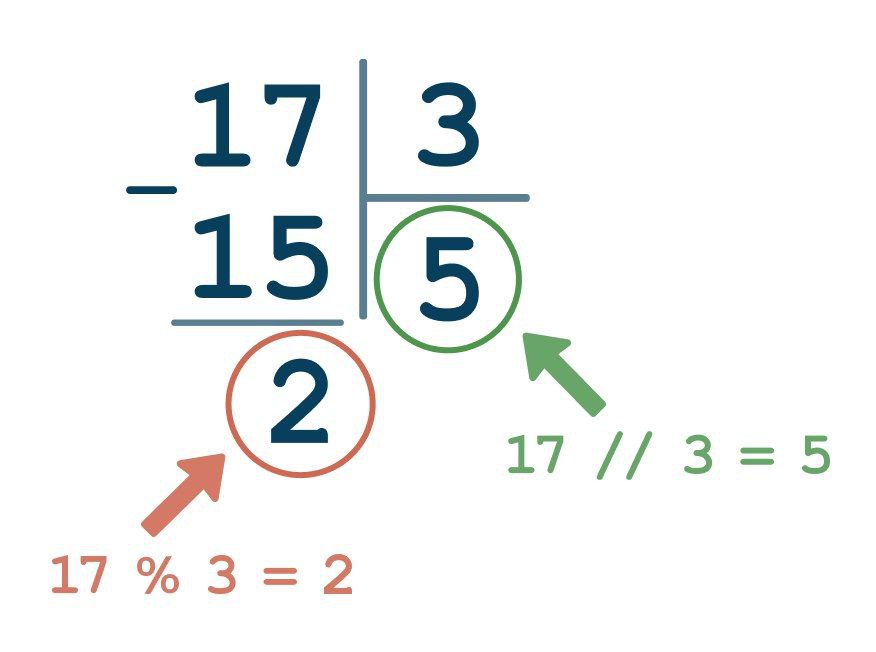
На картинке справа можно увидеть, что при целочисленном делении $17$ на $3$ результатом является число $5$, а остаток при этом равен $2$.

 

 

При делении отрицательных чисел с остатком важно помнить о логике целочисленного деления — округление работает вниз.

Данный код:

print(-7 % 3)
print(-10 % 7)
print(-22 % 10)

выводит

2
4
8

В этом примере ближайшим меньшим и кратным трём числом для $-7$ является $-9$, соответственно остаток равен $2$ и  вычисляется как разница между $-7$ и $-9$.

 Оператор нахождения остатка от деления чаще всего используется в двух случаях:

• Для проверки чётности числа. Следующий код:

print(5 % 2)
print(16 % 2)

выводит

1
0

• Для выделения последней цифры числа. Следующий код:

print(14 % 10)
print(271 % 10)
print(7 % 10)

выводит

4
1
7

 Обратите внимание на то, что для отрицательных чисел операция нахождения остатка будет давать иные результаты. Программа:

print(-14 % 10)
print(-271 % 10)
print(-7 % 10)

выводит

6
9
3

Для того чтобы правильно найти последнюю цифру у отрицательных чисел можно предварительно перевести их в положительные с помощью функции abs().

Функция abs(num) возвращает модуль числа num (для неотрицательных чисел возвращает это же число, а для отрицательных — противоположное по знаку число).

Программа:

print(abs(19) % 10)
print(abs(-271) % 10)
print(abs(-7) % 10)

выводит

9
1
7

Выделение последней цифры с помощью операции % часто используют вместе с целочисленным делением //, ведь последняя позволяет «удалить» последнюю цифру  у числа.

В приведённом ниже коде:

a = 12345
last_gidit = a % 10
a = a // 10

в переменную last_digit записывается последняя цифра исходного числа (цифра $5$), а далее переменная a перезаписывается на значение без выделенной цифры, то есть на $1234$.

При поочерёдном использовании этих двух арифметических операций можно «достать» из числа все его цифры по очереди, начиная с последней. Только важно не забывать, что для отрицательных чисел нужно использовать модуль.

Возведение в степень

Оператор возведения в степень (**) возводит какое-то число в определенную степень.

Этот код:

print(2 ** 3)
print(5 ** 1)
print(10 ** 0)
print(-10 ** 2)
print(4 ** 0.5)

выводит

8
5
1
-100
2.0

Порядок выполнения нескольких операций возведения в степень подряд определяется справа налево.

Данный код:

print(2 ** 3 ** 2)

выводит

512

В этом примере сначала 3 возводится во 2 степень, а затем уже стоящая слева 2 возводится в 9 степень.

Сокращенные арифметические операции

Благодаря сокращенным арифметическим операциям в Python объем кода зачастую можно сократить без потери смысла.

Приведенный ниже код:

a = 1000
a = a + 2
a = a * 3
a = a - 4
a = a // 5
a = a % 2
a = a / 1

можно переписать следующим образом:

a = 1000
a += 2
a *= 3
a -= 4
a //= 5
a %= 2
a /= 1

Сокращенные операторы (+=, *=, -=, /=, //=, %=) удобно использовать в тех случаях, когда приходится изменять значение какой-то конкретной переменной.

Приоритет арифметических операций

Порядок выполнения операций в Python совпадает с привычным нам математическим порядком: наибольшим приоритетом обладает возведение степень, за ним следуют операции умножения и деления, а после уже операции сложения и вычитания.

Приведенный ниже код:

print(5 + 2 ** 2 * 7)
print(3 * 2 + 10)

выводит

33
16

Скобочные выражения

Если в выражении присутствуют скобки, тогда они и определяют порядок выполнения операций.

Данный код:

x = 2 + 2 * 4
y = (2 + 2) * 4
print(x)
print(y)

выводит

10
16

Порядок выполнения всех операций, в том числе выражений в скобках, совпадает с математическим.

С использованием скобок в Python можно вычислять значения длинных и многосоставных выражений.

Например, данное математическое выражение 

$$\frac{5034^2+26\cdot (-70)-(9340+26\cdot 12^3)}{570+12\cdot 45}$$можно переписать в Python:

a = (5034 ** 2 + 26 * (-70) - (9340 + 26 * 12 ** 3)) / (570 + 12 * 45)
print(a)

и получить на выводе $22779.34054054054$.

 Обратите внимание на то, что весь знаменатель дроби взят в отдельные скобки.