Статья Автор: Лебедев Дмитрий Алексеевич

Построение сечения. Аналитический метод

Рассмотрим чертеж куба, на котором отмечен ряд точек:
- вершины (8 точек)
- середины ребер (12 точек)
- середины граней (6 точек)
- центр куба (1 точка)
Итог у нас есть 21 точка.

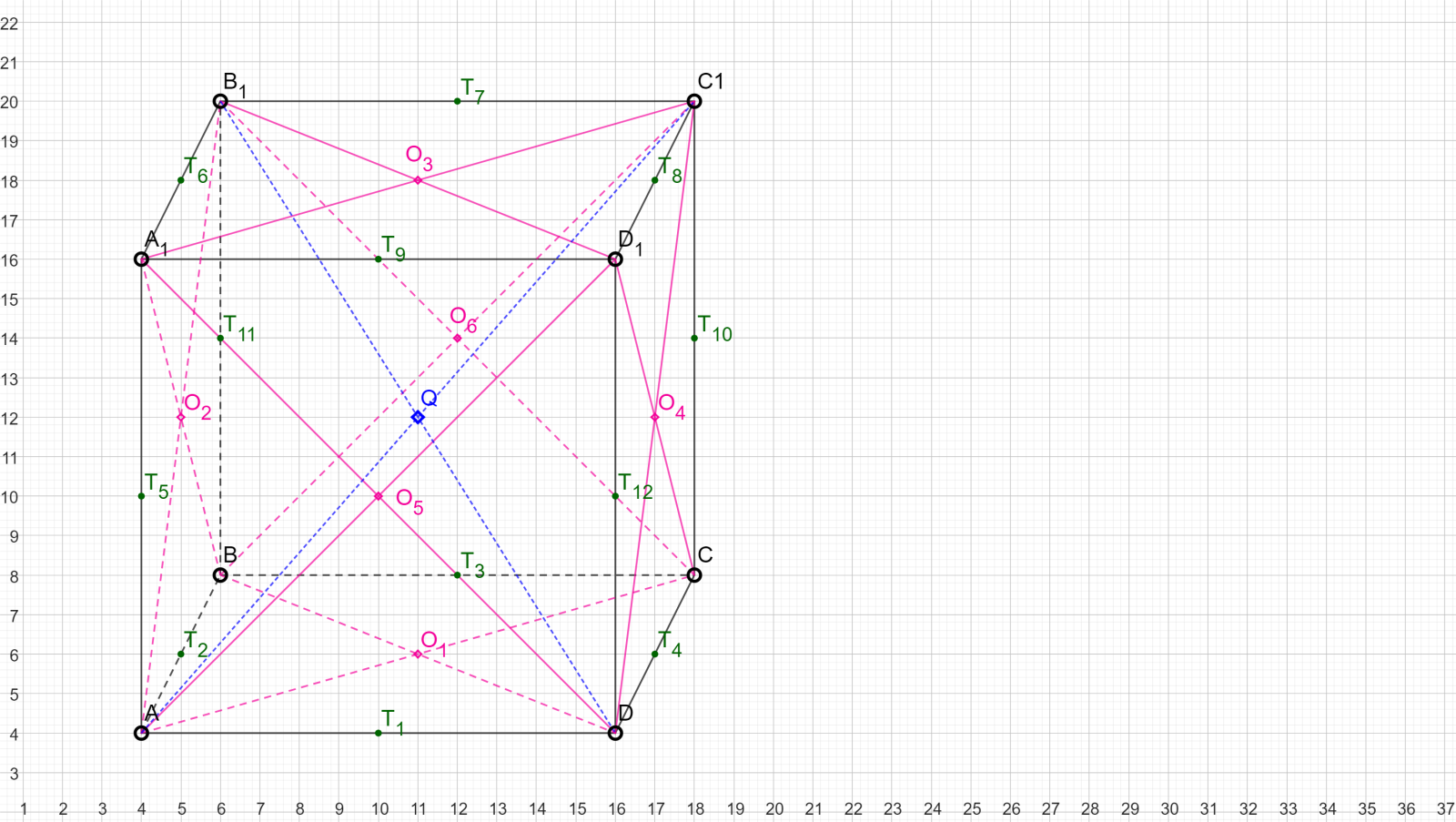
Набор из 4 точек может задавать пирамиду. Такие пирамиды называют кубическими.
web-Чертеж

Пусть дан куб \(ABCDDA_1B_1C_1D_1\)
\(Постройте\ сечение\ куба\ плоскостью\ EFG, \ где:\\E\in\overline{A_1B}\, |\overline{A_1E}|:|\overline{EB_1}|= 1:3\\ \\F \in\overline{AD_1}\, |\overline{AF}|:|\overline{FD_1}|= 2:3\\ \\G \in\overline{DC_1}\, |\overline{DG}|:|\overline{GC_1}|= 1:1 \)

Построение куба, определение точек EFG

import turtle as tr

tt = tr.Pen()
sdvig = [-2, -1, 150] # относительный сдвиг по x/, y, масштаб
tt.speed(10)
# заполняем словарь вершин куба, рисуем куб и подписываем вершины
my_kub = kub_zap((4,2,1)) # параметры - масштаб, смещение 
# рисуем куб с помощью подпрограммы обхода
my_lines(['A','A1','D1','D','A'], my_kub,tt,4) # список имен вершин, словарь вершин, черепашка, параметр рисования (ПС)
my_lines(['A1','B1','C1','D1'], my_kub,tt,4) # ПС - четный: сплошная; нечётный: штрих; значение размер финального круга
my_lines(['D','C','C1'], my_kub,tt,4,)
my_lines(['A','B','B1'], my_kub,tt,5,2)
my_lines(['B','C'], my_kub,tt,5, -10)
tt.color('red')
dot_name(my_kub,my_kub,tt,0,26) # подписываем вершины куба
# рисуем точки условия и диагонали
tt.color('blue') 
E = dot_otnoshenie(my_kub['A1'],my_kub['B'],(1,3))
my_lines(['A1','B'], my_kub,tt,1)
my_kub['E'] = E; dot_name(('E'),my_kub,tt,6);
F = dot_otnoshenie(my_kub['A'],my_kub['D1'],(2,3))
my_lines(['A','D1'], my_kub,tt,1)
my_kub['F'] = F; dot_name(('F'),my_kub,tt,6);
G = dot_otnoshenie(my_kub['D'],my_kub['C1'],(1,1))
my_lines(['D','C1'], my_kub,tt,1)
my_kub['G'] = G; dot_name(('G'),my_kub,tt,6);
tt.hideturtle()      
tr.done()

Решение задание проведем без использования свойст заданных точек, применив "стандартный" метод следа:

пару точек проецируем на плоскость
находим пересечение прямой со "следом" (прямой из проекций)
точка пересечения принадлежит проецируемой плоскости

Точки \(E, F, G \) будем рассматривать как точки на гранях.
Начинаем построение

построим \(E_1 = E +\overrightarrow{A_1A}\ ;\ \ \ \ F_1 =F +\overrightarrow{A_1A};\ \ \ \ G_1 =G +\overrightarrow{A_1A}\)
найдем точки пересечения \(E_2 = \overline{EE_1}\bigotimes \overline{AB}\;\ \ \ F_2 = \overline{FF_1}\bigotimes \overline{AD}\)
рисуем прямые \(EF, E_2F_2, FG, F_2G_2\ до\ пересечений\)
найдем точки пересечения \(P_1 = \overline{EF}\bigotimes \overline{E_2F_2};\ \ \ P_2 = \overline{GF}\bigotimes\overline{F_2G_2}\)
это точки на плоскости \(ABCD\)

Выполняем указанные построения. Оставим (для показа) только нужную часть

import turtle as tr
tt = tr.Pen()
sdvig = (-1, -1, 200) # относительный сдвиг по x/, y, масштаб
cords = (1,1,1) # отношение сторон параллелепипеда
tt.speed(10) # скорость рисования
# заполняем словарь вершин куба, рисуем куб и подписываем вершины
my_kub = kub_zap(cords,1) # параметры - масштаб, смещение 
# рисуем куб с помощью подпрограммы обхода
my_lines(['A','A1','D1','D','A'], my_kub,tt,4) # список имен вершин, словарь вершин, черепашка, параметр рисования (ПС)
my_lines(['A1','B1','C1','D1'], my_kub,tt,4) # ПС - четный: сплошная; нечётный: штрих; значение размер финального круга
my_lines(['D','C','C1'], my_kub,tt,4)
my_lines(['A','B','B1'], my_kub,tt,5)
my_lines(['B','C'], my_kub,tt,5)
#tt.color('red')
#dot_name(my_kub,my_kub,tt,6,0) # подписываем вершины куба
E = dot_otnoshenie(my_kub['T1'],my_kub['O3'],(1,3))
F = dot_otnoshenie(my_kub['O2'],my_kub['O6'],(2,3))
G = dot_otnoshenie(my_kub['B1'],my_kub['O4'],(4,1))
my_line(E,F,tt,5,-100)
sech = {} # Словарь для точек сечения
sech['E'] = E ; sech['F'] = F; sech['G'] = G;
# рисуем точки условия и диагонали
tt.color('blue') 
#my_lines(['T1','O3'], my_kub,tt,1)
#my_lines(['O2','O6'], my_kub,tt,1)
#my_lines(['B1','O4'], my_kub,tt,1)
dot_name(('E','F','G'),sech,tt,6);

# Находим пересечение EF с координатными плоскостями
P21, P11, P61  = xplane(E,F,(0,0,0))
P22, P12, P62  = xplane(F,G,(0,0,0))
P41, P31, P51 = xplane(E,F,cords)
P42, P32, P52 = xplane(F,G,cords)
sech ['P11'] = P11; sech ['P12'] = P12; 
sech ['P21'] = P21; sech ['P22'] = P22; 
sech ['P31'] = P31; sech ['P32'] = P32;
sech ['P41'] = P41; sech ['P42'] = P42;
sech ['P51'] = P51; sech ['P52'] = P52;
sech ['P61'] = P61; sech ['P62'] = P62;
sech['ab'],a,sech['ad'] = xplane(P11,P12,(0,0,0))
sech['cd'],a,sech['bc'] = xplane(P11,P12,cords)
a,sech['ab1'],sech['aa'] = xplane(P21,P22,(0,cords[1],0))
a,b,sech['bb'] = xplane(P21,P22,(cords[0],0,cords[2]))
sech['cd1'],a,sech['bc1']=xplane(P31,P32,cords)
a,b,sech['cc'] = xplane(P41,P42,cords)
sech['dd'],sech['ad1'],a=xplane(P61,P62,cords)
# отбор точек на ребрах куба
ss = {'yz0' : set(),'xz0':set(),'xy0':set(),'yz1' : set(),'xz1':set(),'xy1':set()}
for dt in sech :
  dot =sech[dt]
  if dot == None : continue
  if (dot[0] == 0) and ((dot[1] - cords[1])*dot[1] <=0) and ((dot[2] - cords[2])*dot[2] <=0):  
    if ((dot[1] - cords[1])*dot[1] == 0) or ((dot[2] - cords[2])*dot[2] ==0):
      ss['yz0'].add(dot)
  if (dot[0] == cords[0]) and ((dot[1] - cords[1])*dot[1] <=0) and ((dot[2] - cords[2])*dot[2] <=0):  
    if ((dot[1] - cords[1])*dot[1] == 0) or ((dot[2] - cords[2])*dot[2] == 0):
      ss['yz1'].add(dot)
  if (dot[1] == 0) and ((dot[0] - cords[0])*dot[0] <=0) and ((dot[2] - cords[2])*dot[2] <=0):  
    if ((dot[0] - cords[0])*dot[0] == 0) or ((dot[2] - cords[2])*dot[2] == 0) :
      ss['xz0'].add(dot)
  if (dot[1] == cords[1]) and ((dot[0] - cords[0])*dot[0] <=0) and ((dot[2] - cords[2])*dot[2] <=0):  
    if ((dot[0] - cords[0])*dot[0] == 0) or ((dot[2] - cords[2])*dot[2] == 0) : 
      ss['xz1'].add(dot)
  if (dot[2] == 0) and ((dot[1] - cords[1])*dot[1] <=0) and ((dot[0] - cords[0])*dot[0] <=0):  
    if ((dot[1] - cords[1])*dot[1] == 0) or ((dot[0] - cords[0])*dot[0] == 0):
      ss['xy0'].add(dot)
  if (dot[2] == cords[2]) and ((dot[1] - cords[1])*dot[1] <=0) and ((dot[0] - cords[0])*dot[0] <=0):  
    if ((dot[1] - cords[1])*dot[1] == 0) or ((dot[0] - cords[0])*dot[0] == 0):
      ss['xy1'].add(dot)
ss['yz0'] = list(ss['yz0']);ss['yz1'] = list(ss['yz1'])
ss['xz0'] = list(ss['xz0']);ss['xz1'] = list(ss['xz1'])
ss['xy0'] = list(ss['xy0']);ss['xy1'] = list(ss['xy1'])

# рисуем сечение
tt.color('red'); tt.width(2)
if ss['yz0'] : my_line(ss['yz0'][0],ss['yz0'][-1],tt,1)
if ss['xz1'] : my_line(ss['xz1'][0],ss['xz1'][-1],tt,0)
if ss['xy1'] : my_line(ss['xy1'][0],ss['xy1'][-1],tt,1)
if ss['yz1'] : my_line(ss['yz1'][0],ss['yz1'][-1],tt,0)
if ss['xy0'] : my_line(ss['xy0'][0],ss['xy0'][-1],tt,0)
if ss['xz0'] : my_line(ss['xz0'][0],ss['xz0'][-1],tt,1)
  
  



tt.hideturtle() 
tr.done()

Проводим прямую \(P_1P_2 \) и находим точки пересечения с прямыми \(AB, AD, CD\)

import turtle as tr

   
def xplane(A,B, U = (0,0,0)):
    # нахождение точек пересечения  прямой AB c координатными плоскостями точки u
    Px, Py, Pz = B[0]-A[0],B[1]-A[1],B[2]-A[2]  # направляющих вектор прямой
    Ax, Ay, Az = A[0], A[1], A[2] # координаты точки на прямой
    Ux, Uy, Uz = U[0], U[1], U[2] # координаты узла точки
    Dxy, Dxz, Dyz = None, None, None # инициализация точек пересечения прямой с соотв. плоскостями
    # при вычислениях производим округления
    if Px != 0 : # прямой не параллельна плоскости 'yz'    
        Dyz = (Ux,round((Ay*Px + (Ux-Ax)*Py)/Px,6),round((Az*Px + (Ux-Ax)*Pz)/Px,6))
    if Py != 0:  # прямой не параллельна плоскости 'xz'   
        Dxz = (round((Ax*Py + (Uy-Ay)*Px)/Py,6),Uy,round((Az*Py + (Uy-Ay)*Pz)/Py,6))
    if Pz != 0 :   # прямой не параллельна плоскости 'xy' 
      Dxy = (round((Ax*Pz + (Uz-Az)*Px)/Pz,6),round((Ay*Pz + (Uz-Az)*Py)/Pz,6),Uz)
    return (Dyz,Dxz,Dxy) 

tt = tr.Pen()
sdvig = (-1, -1, 200) # относительный сдвиг по x/, y, масштаб
cords = (1,1,1) # отношение сторон параллелепипеда
tt.speed(10) # скорость рисования
# заполняем словарь вершин куба, рисуем куб и подписываем вершины
my_kub = kub_zap(cords,1) # параметры - масштаб, смещение 
# рисуем куб с помощью подпрограммы обхода
my_lines(['A','A1','D1','D','A'], my_kub,tt,4) # список имен вершин, словарь вершин, черепашка, параметр рисования (ПС)
my_lines(['A1','B1','C1','D1'], my_kub,tt,4) # ПС - четный: сплошная; нечётный: штрих; значение размер финального круга
my_lines(['D','C','C1'], my_kub,tt,4)
my_lines(['A','B','B1'], my_kub,tt,5)
my_lines(['B','C'], my_kub,tt,5)
#tt.color('red')
#dot_name(my_kub,my_kub,tt,6,0) # подписываем вершины куба
E = dot_otnoshenie(my_kub['T1'],my_kub['O3'],(1,3))
F = dot_otnoshenie(my_kub['O2'],my_kub['O6'],(2,3))
G = dot_otnoshenie(my_kub['B1'],my_kub['O4'],(4,1))
sech = {} # Словарь для точек сечения
sech['E'] = E ; sech['F'] = F; sech['G'] = G;
# рисуем точки условия и диагонали
tt.color('blue') 
#my_lines(['T1','O3'], my_kub,tt,1)
#my_lines(['O2','O6'], my_kub,tt,1)
#my_lines(['B1','O4'], my_kub,tt,1)
dot_name(('E','F','G'),sech,tt,6);

# Находим пересечение EF с координатными плоскостями
P21, P11, P61  = xplane(E,F,(0,0,0))
P22, P12, P62  = xplane(F,G,(0,0,0))
P41, P31, P51 = xplane(E,F,cords)
P42, P32, P52 = xplane(F,G,cords)
sech ['P11'] = P11; sech ['P12'] = P12; 
sech ['P21'] = P21; sech ['P22'] = P22; 
sech ['P31'] = P31; sech ['P32'] = P32;
sech ['P41'] = P41; sech ['P42'] = P42;
sech ['P51'] = P51; sech ['P52'] = P52;
sech ['P61'] = P61; sech ['P62'] = P62;
sech['ab'],a,sech['ad'] = xplane(P11,P12,(0,0,0))
sech['cd'],a,sech['bc'] = xplane(P11,P12,cords)
a,sech['ab1'],sech['aa'] = xplane(P21,P22,(0,cords[1],0))
a,b,sech['bb'] = xplane(P21,P22,(cords[0],0,cords[2]))
sech['cd1'],a,sech['bc1']=xplane(P31,P32,cords)
a,b,sech['cc'] = xplane(P41,P42,cords)
sech['dd'],sech['ad1'],a=xplane(P61,P62,cords)
# отбор точек на ребрах куба
ss = {'yz0' : set(),'xz0':set(),'xy0':set(),'yz1' : set(),'xz1':set(),'xy1':set()}
for dt in sech :
  dot =sech[dt]
  if dot == None : continue
  if (dot[0] == 0) and ((dot[1] - cords[1])*dot[1] <=0) and ((dot[2] - cords[2])*dot[2] <=0):  
    if ((dot[1] - cords[1])*dot[1] == 0) or ((dot[2] - cords[2])*dot[2] ==0):
      ss['yz0'].add(dot)
  if (dot[0] == cords[0]) and ((dot[1] - cords[1])*dot[1] <=0) and ((dot[2] - cords[2])*dot[2] <=0):  
    if ((dot[1] - cords[1])*dot[1] == 0) or ((dot[2] - cords[2])*dot[2] == 0):
      ss['yz1'].add(dot)
  if (dot[1] == 0) and ((dot[0] - cords[0])*dot[0] <=0) and ((dot[2] - cords[2])*dot[2] <=0):  
    if ((dot[0] - cords[0])*dot[0] == 0) or ((dot[2] - cords[2])*dot[2] == 0) :
      ss['xz0'].add(dot)
  if (dot[1] == cords[1]) and ((dot[0] - cords[0])*dot[0] <=0) and ((dot[2] - cords[2])*dot[2] <=0):  
    if ((dot[0] - cords[0])*dot[0] == 0) or ((dot[2] - cords[2])*dot[2] == 0) : 
      ss['xz1'].add(dot)
  if (dot[2] == 0) and ((dot[1] - cords[1])*dot[1] <=0) and ((dot[0] - cords[0])*dot[0] <=0):  
    if ((dot[1] - cords[1])*dot[1] == 0) or ((dot[0] - cords[0])*dot[0] == 0):
      ss['xy0'].add(dot)
  if (dot[2] == cords[2]) and ((dot[1] - cords[1])*dot[1] <=0) and ((dot[0] - cords[0])*dot[0] <=0):  
    if ((dot[1] - cords[1])*dot[1] == 0) or ((dot[0] - cords[0])*dot[0] == 0):
      ss['xy1'].add(dot)
ss['yz0'] = list(ss['yz0']);ss['yz1'] = list(ss['yz1'])
ss['xz0'] = list(ss['xz0']);ss['xz1'] = list(ss['xz1'])
ss['xy0'] = list(ss['xy0']);ss['xy1'] = list(ss['xy1'])

# рисуем сечение
tt.color('red'); tt.width(2)
if ss['yz0'] : my_line(ss['yz0'][0],ss['yz0'][-1],tt,1)
if ss['xz1'] : my_line(ss['xz1'][0],ss['xz1'][-1],tt,0)
if ss['xy1'] : my_line(ss['xy1'][0],ss['xy1'][-1],tt,1)
if ss['yz1'] : my_line(ss['yz1'][0],ss['yz1'][-1],tt,0)
if ss['xy0'] : my_line(ss['xy0'][0],ss['xy0'][-1],tt,0)
if ss['xz0'] : my_line(ss['xz0'][0],ss['xz0'][-1],tt,1)
  
  



tt.hideturtle() 
tr.done()

Печать