Линейная регрессия — это самый простой и популярный алгоритм для решения задач регрессии. Его идею можно объяснить одной фразой:
Мы находим прямую линию, которая лучше всего показывает зависимость между одними данными (признаками) и другими (целевой переменной).
Представьте, что у вас есть данные: по оси X — температура на улице, по оси Y — продажи мороженого. Мы рисуем точки и видим, что чем выше температура, тем больше продажи. Линейная регрессия проводит через эти точки такую прямую, чтобы она была как можно "ближе" ко всем точкам сразу. Эта линия и будет нашей моделью-предсказателем.
Как работает линейная регрессия?
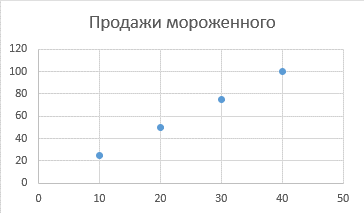
Шаг 1: Рисуем точки
Представьте график, где:
- По горизонтали (ось X) - температура
- По вертикали (ось Y) - количество проданного мороженого
Каждый день - это точка на графике.
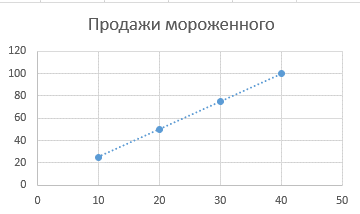
Шаг 2: Проводим линию
Линейная регрессия ищет такую прямую линию, которая лучше всего проходит через все точки.
Шаг 3: Делаем предсказания
Теперь, если нам скажут "завтра будет +25°C", мы:
- Находим 25 на оси X
- Смотрим на линию
- Читаем ответ на оси Y
Математика (очень простая!)
Прямая линия описывается формулой: y = k × x + b
- y - то, что предсказываем (продажи мороженого)
- x - то, что знаем (температура)
- k - насколько сильно влияет температура (угол наклона)
- b - базовое значение (где линия пересекает ось Y)
Пример: y = 3 × x + 10
- При 0°C: y = 3 × 0 + 10 = 10 штук
- При 10°C: y = 3 × 10 + 10 = 40 штук
- При 20°C: y = 3 × 20 + 10 = 70 штук
Задача модели: Найти правильные значения k и b, чтобы линия лучше всего подходила к нашим точкам!