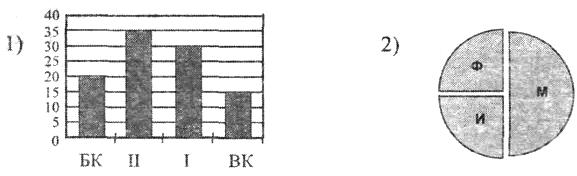
В телеконференции учителей физико-математических школ принимают участие 100 учителей. Среди них есть учителя математики (М), физики (Ф) и информатики (И). Учителя имеют разный уровень квалификации: каждый учитель либо не имеет категории вообще (без категории – БK), либо имеет II, I или высшую (ВК) квалификационную категорию. На диаграмме 1 отражено количество учителей с различным уровнем квалификации, а на диаграмме 2 – распределение учителей по предметам.
Имеются 4 утверждения:
A) Все учителя I категории могут являться учителями математики.
Б) Все учителя I категории могут являться учителями физики.
B) Все учителя информатики могут иметь высшую категорию.
Г) Все учителя математики могут иметь II категорию.
Какое из этих утверждений следует из анализа обеих представленных диаграмм?''''''''
Ответ: 1) А 2)Б 3)В 4)Г