Когда идут ливневые дожди, поля Фермера Джона всегда подтапливаются. И, поскольку имеется рельеф местности, в результате образуются острова, разделенные пространствами воды.
Поля ФД описаны как одноместный рельеф, указанием N (1 <= N <= 100,000) последовательных высот H(1)...H(n). Представим себе, что этот рельеф ограничен с обоих сторон валами бесконечной высоты. Теперь рассмотрим, что случится во время ливневого дождя: сначала водой покрываются нижние регионы, при этом получаются, разъединенные «острова», которые, в конце концов, могут все покрыться водой, если она будет прибывать и прибывать. Если уровень воды становится равным уровню куска земли, то этот кусок считается покрытым водой.
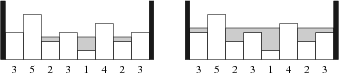
Пример показан на рисунке выше: слева мы добавили 1 единицу воды, и покрыли 4 острова. Затем мы добавили еще 7 единиц воды и теперь только два острова торчат из воды. Вычислите максимальное количество островов, которое мы сможем увидеть, если вода будет прибывать с нуля и до тех пор, пока весь рельеф не скроется под водой. PROBLEM NAME: islands
Формат входных данных
* Строка 1: Целое число N.
* Строки 2..1+N: Строка i+1 содержит высоту H(i). (1 <= H(i) <= 1,000,000,000)
Формат выходных данных
* Строка 1: Одно целое число, определяющее максимальное количество островов, которое получится в один момент времени во время проливного дождя.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
8
3
5
2
3
1
4
2
3
|
4
|