Задача: Прямоугольники
Петя нарисовал на клетчатом листке бумаги красивый рисунок прямоугольной формы. Его младшему брату Васе тоже захотелось порисовать, поэтому он вырезал из того же листка бумаги другой прямоугольник. При этом он не делал лишних разрезов, то есть в результате в листке осталась прямоугольная дырка. Кроме того, линии разреза не проходили (даже частично) по границам рисунка Пети. Более того, по границам рисунка не проходили даже продолжения линий разреза.
Ваша задача – по данным о расположении рисунка и прямоугольной дырки определить, испортил ли Вася рисунок старшего брата, другими словами, есть ли на вырезанном Васей прямоугольнике хотя бы маленький фрагмент рисунка Пети.
Формат входных данных
Вам даны 8 целых чисел - \(x_1, y_1, x_2, y_2, x_3, y_3, x_4, y_4\), где \((x_1, y_1)\) - координаты левого нижнего угла рисунка Пети, \((x_2, y_2)\) - координаты правого верхнего угла рисунка. Аналогично, \((x_3, y_3)\) - координаты левого нижнего угла вырезанного Васей прямоугольника, \((x_4, y_4)\) - координаты правого верхнего угла вырезанного прямоугольника. Гарантируется, что данные прямоугольники невырождены (\(x_1 < x_2\), \(y_1 < y_2\) и аналогичные неравенства для второго набора координат). Листок был не очень большим, поэтому каждое число по модулю не превосходит \(10^4\).
Формат выходных данных
Выведите YES, если Вася испортил рисунок, и NO в противном случае.
Примечание
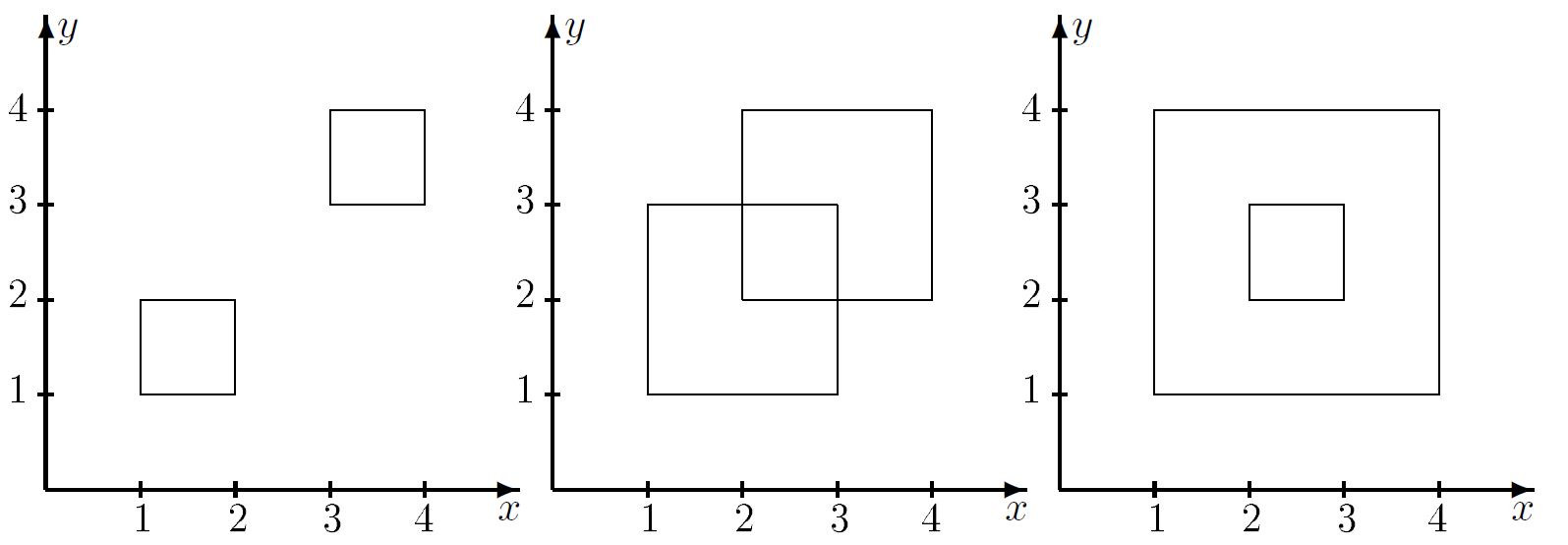
Ваш ответ: