| | | |
|
*Лапта
Бинарный поиск по ответу
Элементарная геометрия
Квадродерево
При игре в лапту одна команда ловит мяч и пытается осалить им бегущего. Игрок другой команды должен, перед тем как бежать, ударить мяч в поле. Известно, на какое максимальное расстояние он может ударить, а также скорости и начальные координаты игроков другой команды. Требуется выбрать направление и силу удара так, чтобы минимальное время, которое потребуется другой команде, чтобы поднять мяч с земли, было наибольшим. (Пока мяч летит, игроки стоят на местах.)
Входные данные:
- в первой строке входных данных содержатся два числа: D — максимальное расстояние удара и N — количество соперников на поле (D и N натуральные числа, \(D <= 1000\), \(N <= 200\));
- в следующих N строках задается по три числа – начальные координаты xi и yi и максимальная скорость vi соответствующего игрока (скорости и координаты — целые числа, \(–1000 <= x_i <= 1000\), \(0 <= y_i <= 1000\), \(0 < v_i <= 1000\)).
Никакие два игрока не находятся изначально в одной точке. Игрок, бьющий мяч, находится в точке с координатами (0,0). Мяч выбивается в точку с неотрицательной ординатой (\(y >= 0\)).
Выходные данные: выведите сначала время, которое потребуется игрокам, чтобы добежать до мяча, а затем координаты точки, в которую нужно выбить мяч. Если таких точек несколько, выведите координаты любой из них. Время и координаты нужно вывести с точностью \(10^{–3}\).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10 2
1 1 1
-1 1 1
|
9.05539
0.00000 10.00000
|
| |
![]()
|
|
Забор по часовой стрелке
Элементарная геометрия
Фермер Джон решил заменить изгородь вокруг своего пастбища.
Эта новая изгородь описывается строкой символов, каждый из которых "N" (north), "E" (east), "S" (south), или "W" (west). Каждый символ описывает 1 метр изгороди. Например, если строка NESW, это означает, что изгородь начинатся одним метром на север, затем 1 метр на восток, затем 1 метр на юг, и затем 1 метр на запад, возвращаясь в стратовую точку.
Изгородь всегда заканчивается в той же позиции, где стартовала, и это - единственная точка, посещенная более одного раза путем изгороди (а стартовая точка, единственная точка посещённая второй раз - в конце пути). Как следствие, изгородь огораживает один связный регион травяного пастбища, даже если этот регион может иметь довольно странную форму.
Фермер Джон хочет узнать, указанный путь обходится по часовой стреле или против часовой стрелки? По часовой стрелке - огороженный регион находится по правую сторону от изгороди, если идти по пути, определённому строкой. Против часовой стрелки - огороженный регион находится по левую сторону от изгороди, если идти по пути, определённому строкой.
Входные данные:
Первая строка содержит целое число N (1≤N≤20). Каждая из последующих N строк содержит строку длиной не менее 4 символов и не более 100, описывающую путь изгороди.
Выходные данные:
Для каждого из N путей, описанных по вводе, выведите строку содержащую "CW" (clockwise - по часовой стрелке) или "CCW" (counterclockwise - против часовой стрелки).
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
2
NESW
WSSSEENWNEESSENNNNWWWS |
CW
CCW |
Оба пути (? символ "пробел") обозначает стартовую точку:
*>*
^ v
<*
*<*<*<*
v ^
*<
*
v ^
* *>*>* *
v ^ v ^
* *<* * *
v ^ v ^
*>*>* *>* |
| |
![]()
|
|
Метеорит
Элементарная геометрия
Беда! К городу N приближается метеорит. Людей уже успели эвакуировать, но домам урона не избежать. Ученые уже выяснили, куда упадет метеорит. Вас, как сотрудника страховой компании, попросили выяснить количество домов, которые пострадают при падении метеорита.
Введём на плоскости прямоугольную систему координат. Город представляет собой прямоугольник n × m . Его левый нижний угол расположен в точке с координатами (0, 0) , а правый верхний угол в точке с координатами ( n - 1, m - 1) . В каждой точке с целыми координатами внутри или на границе этого прямоугольника находится дом. Дома в городе N маленькие, поэтому их можно считать точками.
Известно, что метеорит упал в точку ( x , y ) , а радиус его поражения равен r . Таким образом, все дома города на расстоянии не более r от точки падения метеорита получат повреждения. Найдите количество домов, которые получат повреждения.
Входные данные
Первая строка содержит два целых числа n , m ( 1 ≤ n , m ≤ 500 ) — размеры города N.
Вторая строка содержит три целых числа x , y , r ( - 500 ≤ x , y ≤ 500 ; 0 ≤ r ≤ 500 ) — координаты точки падения метеорита и радиус поражения, соответственно.
Выходные данные
Выведите одно число — количество повреждённых домов.
Примечание
Иллюстрация к тесту из примера: чёрными точками обозначены повреждённые дома, белыми — уцелевшие.

Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 3
1 2 1 |
3 |
| |
![]()
|
|
Сломанный робот
Элементарная геометрия
Конструктив
В 2037-м году для создания научно исследовательской базы на Марс высадился отряд роботов, один из которых отправился собирать информацию о районе дислокации. В данный момент роботу из-за отказа некоторых узлов срочно необходимо вернуться в место закладки будущей базы.
Поверхность Марса в районе высадки десанта можно условно представить в виде плоскости с введенной на ней системой координат, такой, что база находится в точке (0, 0). Робот же остановился в точке (x0, y0). Он может перемещаться в четырёх направлениях:
• «R» — вправо, при этом координата x робота увеличивается на 1;
• «L» — влево, при этом координата x робота уменьшается на 1;
• «U» — вверх, при этом координата y робота увеличивается на 1;
• «D» — вниз, при этом координата y робота уменьшается на 1.
Из-за неисправности робот не может совершить два перемещения подряд в одном направлении.
Помогите роботу вернуться на базу. Робот должен сделать не более 10000 передвижений, иначе он разрядится и не доедет до базы!
Входные данные
В единственной строке входных данных находятся два целых числа x0 и y0 — изначальные координаты робота (−1000 ≤ x0, y0 ≤ 1000).
Выходные данные
В первой строке выведите целое число, не большее 10000 — количество операций, которые должен сделать робот. Во второй строке выведите сами операции. Каждая операция задаётся одной буквой:
вправо — «R» влево — «L», вверх — «U», вниз — «D». Символы необходимо выводить без пробелов между ними.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 1 |
5
DLULD |
Замечание
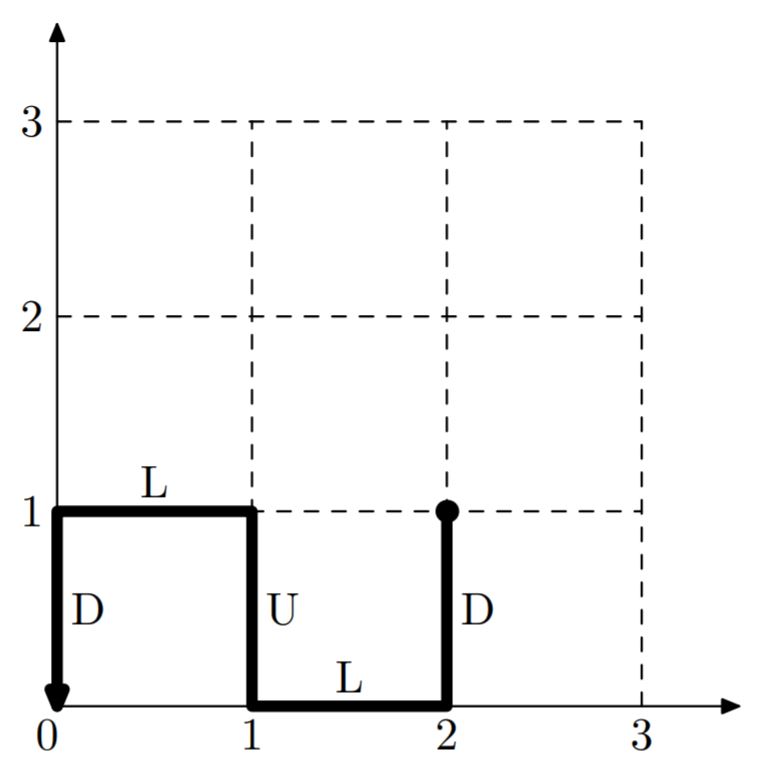
Вы не обязаны выводить кратчайший маршрут. Например, в приведенном примере кратчайший
маршрут состоит из 3 передвижений: влево, вниз, влево.
Иллюстрация к тесту из примера:
| |
![]()
|
|
Треугольник
Элементарная геометрия
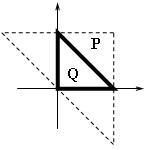
На координатной плоскости расположены равнобедренный прямоугольный треугольник ABC с длиной катета d и точка X. Катеты треугольника лежат на осях координат, а вершины расположены в точках: A (0,0), B (d,0), C (0,d).
Напишите программу, которая определяет взаимное расположение точки X и треугольника. Если точка X расположена внутри или на сторонах треугольника, выведите 0. Если же точка находится вне треугольника, выведите номер ближайшей к ней вершины.
Входные данные
Сначала вводится натуральное число d(не превосходящее 1000), а затем координаты точки X – два целых числа из диапазона от –1000 до 1000.
Выходные данные
Если точка лежит внутри, на стороне треугольника или совпадает с одной из вершин, то выведите число 0. Если точка лежит вне треугольника, то выведите номер вершины треугольника, к которой она расположена ближе всего (1 – к вершине A, 2 – к B, 3 – к C). Если точка расположена на одинаковом расстоянии от двух вершин, выведите ту вершину, номер которой меньше.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5
1 1 |
0 |
Точка лежит внутри треугольника. |
| 2 |
3
-1 -1 |
1 |
Точка лежит вне треугольника и ближе всего к ней вершина A |
| 3 |
4
4 4 |
2 |
Точка лежит на равном расстоянии от вершин B и C,в этом случае нужно вывести ту вершину, у которой номер меньше, т.е. выведено должно быть число 2 |
| 4 |
4
2 2 |
0 |
Точка лежит на стороне треугольника. |
| |
![]()
|
|
Посчитайте лампы
Элементарная геометрия
На новой станции метро, которую планируют открыть в конце этого года, будет N эскалаторов (эскалаторы пронумерованы подряд числами от 1 до N). Эскалаторы имеют длину L и расположены на расстоянии H друг от друга. Шириной эскалатором пренебрежем. Между каждыми двумя соседними эскалаторами (точно посередине) будет установлен ряд ламп. В ряду будет K ламп. Лампы устанавливаются по следующему принципу: всю длину эскалатора L разбивают на K равных отрезков и в середине каждого отрезка устанавливают по лампе (см. рисунок). Всего будет установлено (N–1)*K ламп.
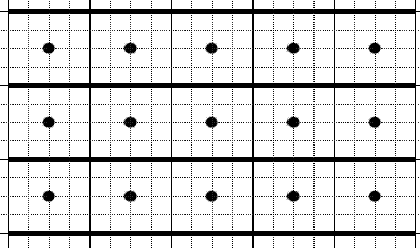
На приведенном рисунке N=4 (эскалаторы показаны жирными <горизонтальными линиями), L=20, H=4, K=5.
Васе удалось проникнуть на эту станцию еще до ее открытия, и даже прокатиться на эскалаторе. Он выбрал эскалатор номер J. Посчитайте, в скольких точках эскалатора (включая его начало и конец) Вася будет видеть не все лампы (так как их будут загораживать другие лампы).
Входные данные
Во входном файле записаны числа N, L, H, K, J. Все числа — натуральные. 2≤N≤35, 1≤L≤1000, 1≤H≤1000, 1≤K≤35, 1≤J≤N.
Выходные данные
В выходной файл выведите одно число — ответ задачи.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 20 4 5 1 |
0 |
| 2 |
4 20 4 5 2 |
11 |
| |
![]()
|
|
Дремучий лес
Элементарная геометрия
Просека — эта такая прямая линия, которая проходит через лес (то есть деревья есть как с одной стороны от этой линии, так и с другой), и при этом она не проходит ни через одно из деревьев леса, а также не касается деревьев. Будем говорить, что лес является дремучим, если в нем нет ни одной просеки.
На плане леса все деревья изображаются кругами. Никакие два круга не пересекаются и не касаются друг друга. Требуется по этому плану определить, является ли лес дремучим.
Входные данные
Во входном файле содержится сначала целое число N — количество деревьев (1 ≤ N ≤ 200). Затем идет N троек чисел, задающих деревья. Первые два числа задают координаты центра, а третье — радиус. Все данные задаются точно, и выражаются вещественными числами, не более чем с 2 знаками после десятичной точки, по модулю не превосходящими 1000.
Выходные данные
В первой строке выходного файла должно содержаться сообщение YES, если лес является дремучим, и NO иначе. Во втором случае вторая строка выходного файла должна содержать координаты двух точек, через которые проходит просека. Все координаты нужно выводить с восемью знаками после десятичной точки, координаты не должны превышать 2000, и расстояние между выданными точками должно быть не меньше 100.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0.00 30.00 25.00
0.00 -30.00 25.00
40.00 0.00 16.00 |
NO
-833.3333340000 -552.7707973875
833.3333340000 552.7707973875 |
| 2 |
3
0.00 30.00 29.00
0.00 -30.00 29.00
40.00 0.00 19.00 |
YES |
| |
![]()
|
|
Клад
Элементарная геометрия
Найти закопанный пиратами клад просто: всё, что для этого нужно – это карта. Как известно, пираты обычно рисуют карты от руки и описывают алгоритм нахождения клада так: «Встаньте около одинокой пальмы. Пройдите тридцать шагов в сторону леса, потом семнадцать шагов в сторону озера, …, наконец десять шагов в сторону большого булыжника. Клад находится под ним». Большая часть таких указаний просто сводится к прохождению какого-то количества шагов в одном из восьми направлений (1 – север, 2 – северо-восток, 3 – восток, 4 – юго-восток, 5 – юг, 6 – юго-запад, 7 – запад, 8 – северо-запад) (см. рис). Длина шага в любом направлении равна 1.
Путешествие по такому пути обычно является прекрасным способом посмотреть окрестности, однако в наше время постоянной спешки ни у кого нет времени на это. Поэтому кладоискатели хотят идти напрямую в точку, где зарыт клад. Например, вместо того, чтобы проходить три шага на север, один шаг на восток, один шаг на север, три шага на восток, два шага на юг и один шаг на запад, можно пройти напрямую, использовав около 3.6 шага (см. рис).
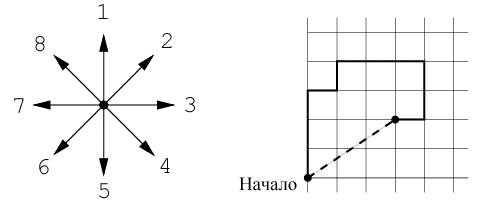
Вам необходимо написать программу, которая по указаниям пиратов определяет точку, где зарыт клад.
Формат входных данных
Первая строка содержит число N – число указаний (1≤N≤40). Последующие N строк содержат сами указания – номер направления (целое число от 1 до 8) и количество шагов (целое число от 1 до 1000). Числа разделены пробелами.
Формат выходных данных
Выведите координаты X и Y точки (два вещественных числа, разделённые пробелом), где зарыт клад, считая, что ось Ox направлена на восток, а ось Oy – на север. В начале кладоискатель должен стоять в начале координат. Координаты необходимо вывести с погрешностью не более 10-3.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
1 3
3 1
1 1
3 3
5 2
7 1 |
3.000 2.000 |
| 2 |
1
8 10 |
-7.071 7.071 |
| |
![]()
|
|
Целые точки
Элементарная геометрия
НОД и алгоритм Евклида
Многоугольники. Выпуклые оболочки
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Формат входных данных
В первой строке содержится N (3 ≤N ≤1000) – число вершин многоугольника. В последующих N строках идут координаты (Xi, Yi) вершин многоугольника в порядке обхода по часовой стрелке. Xi и Yi - целые числа, по модулю не превосходящие 1000000.
Формат выходных данных
Вывести одно число – искомое число точек.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
-1 -1
-1 1
1 1
1 -1 |
1 |
| 2 |
3
0 0
0 2
2 0
|
0 |
| |
![]()
|
|
Параллелограмм
Элементарная геометрия
На уроке геометрии семиклассники Вася и Петя узнали, что такое параллелограмм. На перемене после урока они стали играть в игру: Петя называл координаты четырех точек в произвольном порядке, а Вася должен был ответить, являются ли эти точки вершинами параллелограмма.
Вася, если честно, не очень понял тему про параллелограммы, и ему требуется программа, умеющая правильно отвечать на Петины вопросы.
Напомним, что параллелограммом называется невырожденный четырехугольник, противоположные стороны которого параллельны.
Входные данные
В первой строке входного файла записано целое число N (1 ≤ N ≤ 10) - количество заданных Петей вопросов. Каждая из N последующих строк содержит описание четырех точек - четыре пары целых чисел X и Y (−100 ≤ X ≤ 100, −100 ≤ Y ≤ 100), обозначающих координаты точки.
Выходные данные
Для каждого из вопросов определите, образуют ли данные точки параллелограмм. Если они образуют параллелограмм, то выведите номера этих точек в одной строке через пробел в порядке обхода параллелограмма. Начинать обход можно с любой из вершин. Если они не образуют параллелограмм, выведите в этой строке одно число 0. Ответ на каждый из запросов должен быть в отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1 1 4 2 3 0 2 3
1 1 5 2 2 3 3 0
0 0 5 1 6 3 1 2 |
1 3 2 4
0
1 2 3 4 |
| |
![]()
|
|
Уравнение прямой
Элементарная геометрия
Входные данные
Четыре числа – координаты двух различных точек на прямой.
Выходные данные
Три числа – коэффициенты A, B и C уравнения этой прямой.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 0 2 1 |
1 -1 -1 |
| |
![]()
|
|
Уравнение прямой - 2
Элементарная геометрия
Входные данные
Четыре числа – координаты точки на прямой и координаты вектора нормали к этой прямой.
Выходные данные
Три числа – коэффициенты A, B и C уравнения этой прямой.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
0 0 1 1 |
1 1 0 |
| |
![]()
|
|
Принадлежность точки прямой
Элементарная геометрия
Входные данные
Пять чисел – координаты точки и коэффициенты A, B и C уравнения прямой.
Выходные данные
Одна строка “YES”, если точка принадлежит прямой, и “NO” в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 7 2 -3 5 |
YES |
| |
![]()
|
|
Расстояние от точки до прямой
Элементарная геометрия
Входные данные
Пять чисел – координаты точки и коэффициенты A, B и C уравнения прямой.
Выходные данные
Одно число – расстояние от точки до прямой.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 5 0 -4 8 |
3.00000 |
| |
![]()
|
|
Расстояние от точки до луча
Элементарная геометрия
Входные данные
Шесть чисел – координаты точки и координаты начала и конца вектора.
Выходные данные
Одно число – расстояние от точки до луча, определяемого вектором.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 3 0 0 4 0 |
3.00000 |
| 2 |
-1 1 0 0 4 0 |
1.41421 |
| |
![]()
|
|
Расстояние от точки до отрезка
Элементарная геометрия
Входные данные
Шесть чисел – координаты точки и координаты концов отрезка.
Выходные данные
Одно число – расстояние от точки до отрезка.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
0 0 0 0 4 0 |
0.00000 |
| 2 |
4 0 0 0 4 0 |
0.00000 |
| |
![]()
|
|
Пересечение отрезков
Элементарная геометрия
Входные данные
Восемь чисел – координаты концов двух отрезков.
Выходные данные
Одна строка “YES”, если отрезки имеют общие точки, и “NO” в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 2 1 2
1 2 1 2 |
YES |
| 2 |
3 3 5 6
5 6 3 3 |
YES |
| |
![]()
|
|
Пересечение двух прямых
Элементарная геометрия
Входные данные
Шесть чисел – коэффициенты A, B и C нормального уравнения двух различных непараллельных прямых (сначала для одной прямой, затем для другой).
Выходные данные
Два числа – координаты точки их пересечения.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 -4 0 0 -3 6 |
2.00000 2.00000 |
| |
![]()
|
|
Биссектриса
Элементарная геометрия
Входные данные
Шесть чисел – координаты точек X, Y и Z.
Выходные данные
Три числа – коэффициенты уравнения биссектрисы угла YXZ.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
0 0 1 0 0 1 |
1.000000 -1.000000 0.000000 |
| 2 |
0 0 1 3 1 -3 |
0.000000 -0.632456 0.000000 |
| |
![]()
|
|
Касательная к окружности
Элементарная геометрия
Входные данные
Пять чисел – координаты центра и радиус окружности, координаты точки.
Выходные данные
В первой строке одно число K, равное количеству точек пересечения касательных к окружности из заданной точки с самой окружностью. Далее в K строках координаты самих точек.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2 2 2 5 |
2
0.50929 3.33333
3.49071 3.33333 |
| |
![]()
|
|
Окружность и прямая
Элементарная геометрия
Входные данные
Шесть чисел – координаты центра и радиус окружности и коэффициенты A, B и C нормального уравнения прямой.
Выходные данные
В первой строке одно число K, равное количеству точек пересечения прямой с окружностью. Далее в K строках координаты самих точек.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 3 1 1 -1 0 |
2
3.00000 3.00000
2.00000 2.00000 |
| |
![]()
|
|
Две окружности
Элементарная геометрия
Входные данные
Шесть чисел – координаты центра и радиусы двух окружностей.
Выходные данные
В случае, если количество общих точек окружностей конечно, в первой строке вывести одно число K, равное этому количеству, далее в K строках координаты самих точек. Если указанных точек бесконечно много, вывести единственное число “3”.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4 5 11 4 2 |
0 |
| 2 |
3 4 5 9 4 2 |
2
7.75000 5.56125
7.75000 2.43875 |
| |
![]()
|
|
Длина дуги
Элементарная геометрия
Входные данные
Семь чисел – координаты центра и радиус окружности (возможно, вырожденной) и вещественные координаты двух точек на ней, с точностью до пятого знака после запятой.
Выходные данные
Одно число – длина меньшей дуги окружности, заключённой между указанными точками.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
0 0 1 0 1 1 0 |
1.57080 |
| |
![]()
|
|
Сортировка точек
Структуры
Использование сортировки
Элементарная геометрия
Выведите все исходные точки в порядке возрастания их расстояний от начала координат.
Создайте структуру Point и сохраните исходные данные в массиве структур Point.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n, затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Величина n не превосходит 100, все исходные координаты – целые числа, не превосходящие 103.
Выходные данные
Необходимо вывести все исходные точки в порядке возрастания их расстояний от начала координат. Программа выводит только координаты точек, их количество выводить не надо.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
1 2
2 3 |
1 2
2 3 |
| |
![]()
|
|
Поиск вершины по центру вписанной окружности (I, инцентр)
Бинарный поиск
Элементарная геометрия
Вычислительная геометрия
Точка I – центр вписанной окружности треугольника АВС (инцентр).
Найдите абсциссу вершины C (координату x), если известно:
- координаты точек A и B;
- координата точки D, лежащей на прямой ВС;
- точка I лежит на прямой ED (координаты точки E известны);
- для координат выполняются условия: Ax<Cx<Bx;
Входные данные: в 1-й строке вводятся значения Ax, Ay, Bx, By Dx,Dy, Ex, Ey – координаты точек A, B, D, E
Все значения целые числа в интервале [-1000;1000].
Выходные данные: ответ на задание с точностью не менее 10-5.
Пример:
| Входные данные |
Выходные данные |
| 1 1 7 3 8 1 1 7 |
4.348182 |
| -1 3 9 1 8 -1 -1 1 |
6.500895 |
| |
![]()
|
|
Поиск вершины по центру описанной окружности (O)
Бинарный поиск
Элементарная геометрия
Вычислительная геометрия
Точка O – центр описанной окружности треугольника АВС.
Найдите абсциссу вершины C (координату x), если известно:
- координаты точек A и B;
- координата точки D, лежащей на прямой ВС;
- точка O лежит на прямой ED (координаты точки E известны);
- для координат выполняются условия: Ax<Cx<Bx;
Входные данные: в 1-й строке вводятся значения Ax, Ay, Bx, By Dx,Dy, Ex, Ey – координаты точек A, B, D, E
Все значения целые числа в интервале [-1000;1000].
Выходные данные: ответ на задание с точностью не менее 10-5.
Пример:
| Входные данные |
Выходные данные |
| 1 1 6 3 7 1 0 6 |
3.784 |
| 1 2 5 1 6 -1 1 5 |
3.207692 |
| |
![]()
|
|
Поиск вершины по ортоцентру (H)
Бинарный поиск
Элементарная геометрия
Вычислительная геометрия
Точка H – центр пересечения высот треугольника (ортоцентр) АВС.
Найдите абсциссу вершины C (координату x), если известно:
- координаты точек A и B;
- координата точки D, лежащей на прямой ВС;
- точка H лежит на прямой ED (координаты точки E известны);
- для координат выполняются условия: Ax<Cx<Bx;
Входные данные: в 1-й строке вводятся значения Ax, Ay, Bx, By Dx,Dy, Ex, Ey – координаты точек A, B, D, E
Все значения целые числа в интервале [-1000;1000].
Выходные данные: ответ на задание с точностью не менее 10-5.
Пример:
| Входные данные |
Выходные данные |
| 1 1 6 3 9 1 1 5 |
2.454545 |
| 1 2 5 1 6 -1 1 5 |
3.196078 |
| |
![]()
|
|
Треугольник. Поиск вершины по положению центроида
Бинарный поиск
Элементарная геометрия
Вычислительная геометрия
Точка G – центр пересечения медиан треугольника (центроид) АВС.
Найдите абсциссу вершины C (координату x), если известно:
- координаты точек A и B;
- координата точки D, лежащей на прямой ВС;
- точка G лежит на прямой ED (координаты точки E известны);
- для координат выполняются условия: Ax<Cx<Bx;
Входные данные: в 1-й строке вводятся значения Ax, Ay, Bx, By Dx,Dy, Ex, Ey – координаты точек A, B, D, E
Все значения целые числа в интервале [-1000;1000].
Выходные данные: ответ на задание с точностью не менее 10-5.
Пример:
| Входные данные |
Выходные данные |
| 2 2 7 1 6 3 3 4 |
3.6 |
| 0 0 5 1 3 4 0 0 |
1.0 |
| |
![]()
|
|
Длина отрезка
Элементарная геометрия
Информатика
Длина отрезка
Даны четыре действительных числа: x1, y1, x2, y2. Напишите программу, вычисляющую расстояние между точками с координатами (x1,y1) и (x2,y2).
Входные данные.
Четыре действительных числа.
Выходные данные.
Результат работы программы. Точность вычисления не менее 5 знаков.
Примеры
| входные данные |
выходные данные |
0
0
1
1 |
1.41421 |
| |
![]()
|
|
Принадлежит ли точка квадрату-1
Элементарная геометрия
Условный оператор
Принадлежит ли точка квадрату - 1
Даны два действительных числа x и y. Проверьте, принадлежит ли точка с координатами (x,y) заштрихованному квадрату (включая его границу).
Если точка принадлежит квадрату, выведите слово YES, иначе выведите слово NO. На рисунке сетка проведена с шагом 1.

Входные данные.
Два действительных числа.
Выходные данные.
Ответ на задачу.
Примеры
| входные данные |
выходные данные |
0
0 |
YES |
3
-7 |
NO |
| |
![]()
|
|
Принадлежит ли точка квадрату - 2
Элементарная геометрия
Условный оператор
Принадлежит ли точка квадрату - 2
Даны два действительных числа x и y. Проверьте, принадлежит ли точка с координатами (x,y) заштрихованному квадрату (включая его границу).
Если точка принадлежит квадрату, выведите слово YES, иначе выведите слово NO. На рисунке сетка проведена с шагом 1.

Входные данные.
Два действительных числа.
Выходные данные.
Ответ на задачу.
Примеры
| входные данные |
выходные данные |
0
0 |
YES |
1
1 |
NO |
| |
![]()
|
|
Принадлежит ли точка кругу
Элементарная геометрия
Условный оператор
Принадлежит ли точка кругу
Даны пять действительных чисел: x, y, xc, yc, r.
Проверьте, принадлежит ли точка (x,y) кругу с центром (xc,yc) и радиусом r.
Если точка принадлежит кругу, выведите слово YES, иначе выведите слово NO.
Входные данные.
Два действительных числа.
Выходные данные.
Ответ на задачу.
Примеры
| входные данные |
выходные данные |
0.5
0.5
0
0
1
|
YES |
0.5
0.5
1
1
0.1
|
NO |
| |
![]()
|
|
Принадлежит ли точка области
Элементарная геометрия
Условный оператор
Принадлежит ли точка области
Даны два действительных числа x и y. Проверьте, принадлежит ли точка с координатами (x,y) данной закрашенной области:

Если точка принадлежит области (область включает границы), выведите слово YES, иначе выведите слово NO.
На рисунке сетка проведена с шагом 1.
Входные данные.
Два действительных числа.
Выходные данные.
Ответ на задачу.
Примеры
| входные данные |
выходные данные |
-2
2 |
YES |
-2
1 |
NO |
| |
![]()
|
|
Принадлежность точки отрезку
Элементарная геометрия
Принадлежность точки отрезку
Входные данные
Вводятся шесть чисел - координаты точки и координаты концов отрезка.
Выходные данные
Выведите одну строку "YES", если точка принадлежит отрезку, и "NO" в противном случае.
Примеры
| входные данные |
выходные данные |
4 0 4 2 4 5
|
NO |
4 2 4 2 4 5
|
YES |
| |
![]()
|
|
Угол между векторами
Элементарная геометрия
Угол между векторами
Входные данные
Четыре числа - координаты двух векторов. Все числа целые, по модулю не превышающие 1000.
Выходные данные
Одно число - величина неориентированного угла между ними с точностью до пятого знака после запятой.
Примеры
| входные данные |
выходные данные |
2 1 1 2
|
0.64350
|
-2 1 -1 2
|
0.64350
|
| |
![]()
|
|
Полярное расстояние
Элементарная геометрия
Полярное расстояние
Заданы полярные координаты двух точек на плоскости. Требуется найти расстояние между этими точками.
Входные данные
Вводятся 4 числа в две строки.
Числа первой строки два задают радиус и полярный угол первой точки,
числа второй строки - полярные координаты второй.
Обратите внимание: все углы задаются в градусах.
Выходные данные
Выведите расстояние между точками с точностью не меньше, чем в пять знаков.
Примеры
| входные данные |
выходные данные |
3 90
4 180
|
5.0
|
5 10
5 190
|
10.0
|
| |
![]()
|
|
Пересекаются ли два луча
Элементарная геометрия
Пересекаются ли два луча
Даны два луча: AB и CD (A и C - вершины лучей, B и D лежат на лучах). Проверьте, пересекаются ли они.
Входные данные
Программа получает на вход координаты точек A, B, C, D.
Все координаты - целые, не превосходят 100 по модулю.
Координаты каждой точки вводятся в отдельной строке.
Выходные данные
Программа должна вывести слово YES или NO
Примеры
| входные данные |
выходные данные |
0 1
1 2
1 -1
1 0
|
YES
|
0 0
1 0
0 1
1 2
|
NO
|
| |
![]()
|
|
Точка пересечения медиан
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Точка пересечения медиан
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа X, Y, задающие координаты точки пересечения медиан в треугольнике, образованном исходными точками.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
1 1 2 4 3 2
|
2.00000 2.33333
|
2 4 3 2 1 1
|
2.00000 2.33333
|
| |
![]()
|
|
Точка пересечения высот
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Точка пересечения высот
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа X, Y, задающие координаты точки пересечения высот в треугольнике, образованном исходными точками.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
1 1 2 4 3 2
|
3.0 2.0
|
10 0 12 2 14 5
|
37.0 -18.0
|
| |
![]()
|
|
Вписанная окружность
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Вписанная окружность
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите три числа X, Y, R, задающие координаты центра и радиус окружности, вписанной в треугольник, образованый исходными точками.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
| 1 1 2 4 3 2 |
2.12132 2.292893 0.65493
|
10 0 12 2 14 5
|
11.878925 2.099258 0.1557984
|
| |
![]()
|
|
Описанная окружность
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Описанная окружность
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа X, Y, R, задающие координаты центра и радиус окружности, описанной вокруг треугольника, образованного исходными точками.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
| 1 1 2 4 3 2 |
1.50000 2.50000 1.58114
|
10 0 12 2 14 5
|
-0.50000 12.50000 16.32483
|
| |
![]()
|
|
Точка пересечения двух прямых
Элементарная геометрия
Вычислительная геометрия
Точка пересечения прямых
На плоскости даны две прямые. Каждая прямая задается парой точек, через которые она проходит.
Требуется установить, пересекаются ли эти прямые, и найти координаты точки пересечения.
Выходные данные
Если прямые не пересекаются, выведите одно число 0. Если прямые совпадают, выведите 2.
Если прямые пересекаются ровно в одной точке, то выведите сначала число 1,
а затем два вещественных числа - координаты точки пересечения.
Координаты точки пересечения необходимо определить с точностью не менее 5 знаков.
Примеры
| входные данные |
выходные данные |
0 0 1 1
1 0 -1 2
|
1 0.50 0.50
|
1 2 3 4
0 3 4 7
|
0
|
1 2 3 4
3 4 1 2
|
2 |
| |
![]()
|
|
Расстояние от точки до прямой
Элементарная геометрия
Вычислительная геометрия
Расстояние от точки до прямой
Определите расстояние от точки до прямой.
Входные данные
Пять чисел – координаты точки и коэффициенты A, B и C уравнения прямой.
Все числа целые и по модулю не превосходят 10000.
Выходные данные
Одно число – расстояние от точки до прямой. Точность вычисления не менее 5 знаков.
Примеры
| входные данные |
выходные данные |
1 5 0 -4 8
|
3.0 |
1 5 -4 0 8
|
1.0
|
| |
![]()
|
|
Перпендикулярная прямая
Элементарная геометрия
Перпендикулярная прямая
По уравнению прямой и координатам некоторой точки (точка может быть как на прямой, так и вне ее)
определить уравнение прямой, проходящей через заданную точку и перпендикулярную заданой прямой.
Входные данные
Пять чисел - коэффициенты A, B и C уравнения прямой и координаты некоторой точки X, Y (точка может быть как на прямой, так и вне ее).
Все числа целые, по модулю не превосходят 10000.
Выходные данные
Выведите три числа - коэффициенты A, B и C уравнения прямой, перпендикулярной заданной и проходящей через заданную точку.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры
| входные данные |
выходные данные |
0 -4 8 5 0
|
-4.0 0.0 20.0
|
-4 0 8 5 0
|
0.0 4.0 0.0
|
| |
![]()
|
|
Параллельная прямая
Элементарная геометрия
Параллельная прямая
Задана прямая и неотрицательная величина R. Определите уравнения любой из прямых, параллельных заданной и лежащей от неё на расстоянии R.
Входные данные
Четыре числа - коэффициенты A, B и C уравнения прямой и величина R.
Все числа целые, по модулю не превосходят 10000.
Выходные данные
Выведите три числа - коэффициенты A, B и C уравнения любой из прямых,
параллельных заданной и лежащих от неё на расстоянии R. Все значения должны быть вычислены с точностью не меннее 5 знаков.
Примеры
| входные данные |
выходные данные |
0 -4 8 5
|
0 -4 -12.0
|
|
|
| |
![]()
|
|
Положение точек вне прямой
Элементарная геометрия
Положение точек вне прямой
Определите положение двух точек относительно заданной прямой.
Известно, что точки на прямой не лежат.
Входные данные
Семь чисел - координаты двух точек вне прямой и коэффициенты A, B и C её уравнения.
Все числа целые и по абсолютному значению не превосходят 10000
Выходные данные
Выведите одну строку: "YES", если точки лежат по одну сторону прямой, и "NO" в противном случае.
Примеры
| входные данные |
выходные данные |
0 1 1 0 0 -4 8
|
YES
|
0 0 3 3 0 -4 8
|
NO
|
| |
![]()
|
|
Ускорители для Деда Мороза
Динамическое программирование на таблицах
Элементарная геометрия
Алгоритмы на графах
Дед Мороз за ночь должен посетить N городов. У него есть двумерный план расположения всех городов. План нарисован в декартовой системе координат, в которой точкой (0, 0) обозначено место старта Деда Мороза. Каждый город на плане отмечен точкой с координатой (Xi, Yi). Также на карте обозначены M точек с координатами (Pi, Qi), в которых расположены ускорители. Чтобы успеть разнести все подарки, Дед Мороз может воспользоваться ускорителем, который увеличивает его скорость в два раза (а может им и не пользоваться).
Дед Мороз в Новогоднюю ночь начинает с места старта, посещает все N городов и возвращается обратно.
Начальная скорость Деда Мороза равна 1. Найдите наименьшее время, необходимое Деду Морозу, чтобы посетить все города и вернуться обратно. Временем, при котором он раскладывает все подарки будем пренебрегать!
Входные данные
Первая строка входных данных содержит два целых числа N и M (1 <= N <= 12, 0 <= M <=5). Следующие N строк содержат координаты городов (Xi, Yi). Далее идут M строк с координатами ускорителей (Pi, Qi). Все координаты различны и среди них нет координаты (0, 0).
Выходные данные
Выведите ответ на задачу, с точностью не менее 6 знаков после запятой.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
2 1
1 1
0 1
1 0 |
2 1
1 1
0 1
1 0 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1 от начала координат до ускорителя 1 со скоростью 1, затратив время 1.
- Пройти расстояние 1 от ускорителя 1 до города 1 со скоростью 2, затратив время 0,5.
- Пройти расстояние 1 от города 1 до города 2 со скоростью 2, затратив время 0,5.
- Пройти расстояние 1 от города 2 до начала координат со скоростью 2, затратив время 0,5.
|
| 2 |
2 1
1 1
0 1
100 0 |
3.4142135624 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1.41... от начала координат до города 1 со скоростью 1, затратив время 1.41....
- Пройти расстояние 1 от города 1 до города 2 со скоростью 1, затратив время 1.
- Пройти расстояние 1 от города 2 до начала координат со скоростью 1, затратив время 1.
|
| 3 |
1 2
4 4
1 0
0 1 |
4.3713203436 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1 от начала координат до ускорителя 1 со скоростью 1, затратив время 1.
- Пройти расстояние 1,41... от ускорителя 1 до ускорителя 2 со скоростью 2, затратив время 0,707....
- Пройти расстояние 5 от ускорителя 2 до города 1 со скоростью 4, затратив время 1,25.
- Пройти расстояние 5,65... от города 1 до начала координат со скоростью 4, затратив время 1,41....
|
| |
![]()
|
|
Описанная окружность
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Описанная окружность
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа X, Y, R, задающие координаты центра и радиус окружности, описанной вокруг треугольника, образованного исходными точками.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
| 1 1 2 4 3 2 |
1.50000 2.50000 1.58114
|
10 0 12 2 14 5
|
-0.50000 12.50000 16.32483
|
| |
![]()
|
|
Вписанная окружность
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Вписанная окружность
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа X, Y, R, задающие координаты центра и радиус окружности, вписанной в треугольник, образованый исходными точками.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
| 1 1 2 4 3 2 |
2.12132 2.292893 0.65493
|
10 0 12 2 14 5
|
11.8789 2.099258 0.1557984
|
| |
![]()
|
|
Приданое для Василисы
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Приданое для Василисы
Тридевятое царство царя Василия имеет треугольную форму. Он решил выдать замуж свою любимую дочь Василису и отдать ей в приданое часть своего царства. Царь Василий очень любит геометрию, поэтому вначале выполнил на карте царства следующие действия:
- из самого большого угла царь провел высоту к противоположной стороне;
- в самом маленьком угле царь провел биссектрису;
- из среднего угла царь провел медиану;
Образовавшийся треугольник царь решил отдать в приданое.
Зная координаты вершин царства, определите отношение площади предпологаемого приданого к площади всего царства.
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Это координаты "вершин" царства. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите одно число - отношение площадей приданого и царства.
Ответе должен быть выдан с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
0 1 -2 3 8 3
|
0.07324155 |
-1 2 10 11 0 1
|
0.1600294
|
| |
![]()
|
|
Приданое для Елены
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Приданое для Елены
Тридевятое царство царя Егора имеет треугольную форму. Он решил выдать замуж свою любимую дочь Елену и отдать ей в приданое часть своего царства. Царь Егор очень любит геометрию, поэтому вначале выполнил на карте царства следующие действия:
- из самого большого угла царь провел высоту к противоположной стороне;
- в среднем угле царь провел биссектрису;
- из самого маленького угла царь провел медиану;
Образовавшийся треугольник царь решил отдать в приданое.
Зная координаты вершин царства, определите отношение площади предпологаемого приданого к площади всего царства.
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Это координаты "вершин" царства. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите одно число - отношение площадей приданого и царства.
Ответе должен быть выдан с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
0 1 -2 3 8 3
|
0.0003479 |
-1 2 10 11 0 1
|
0.01717956
|
| |
![]()
|
|
Приданое для Ирины
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Приданое для Ирины
Тридевятое царство царя Игоря имеет треугольную форму. Он решил выдать замуж свою любимую дочь Елену и отдать ей в приданое часть своего царства. Царь Игорь очень любит геометрию, поэтому вначале выполнил на карте царства следующие действия:
- из самого большого угла царь провел высоту к противоположной стороне;
- в среднем угле царь провел биссектрису;
- из самого большого угла царь провел медиану;
Образовавшийся треугольник царь решил отдать в приданое.
Зная координаты вершин царства, определите отношение площади предпологаемого приданого к площади всего царства.
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Это координаты "вершин" царства. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите одно число - отношение площадей приданого и царства.
Ответе должен быть выдан с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
0 1 -2 3 8 3
|
0.06349376 |
-1 2 10 11 0 1
|
0.0739834
|
| |
![]()
|
|
Столица царя Иосифа
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Столица царя Иосифа
Тридевятое царство царя Иосифа имеет треугольную форму. Столица царства расположена в центроиде треугольника (точка О). Царь Иосиф решил построить новую столицу. Царь очень любит геометрию, поэтому вначале выполнил на карте царства следующие действия:
- из самого большого угла царь провел высоту и определил её основание (точку D);
- в среднем угле царь провел биссектрису и определил её основание (точку E);
- из самого маленького угла царь провел медиану и определил её основание (точку F);
Новую столицу царь Иосиф решил расположить в центроиде треугольника DEF (точка G).
Зная координаты вершин царства, определите расстояние между столицами царства (длина отрезка GO).
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Это координаты "вершин" царства. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите одно число - ответ на задачу.
Ответе должен быть выдан с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
0 1 -2 3 8 3
|
1.75530286 |
-1 2 10 11 0 1
|
4.24704495
|
| |
![]()
|
|
Описанная окружность
Вычислительная геометрия
Элементарная геометрия
Многоугольники. Выпуклые оболочки
Описанная окружность
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3.
Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа X, Y, R, задающие координаты центра и радиус окружности, описанной вокруг треугольника, образованного исходными точками.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры:
| Входные данные |
Выходные данные |
| 1 1 2 4 3 2 |
1.50000 2.50000 1.58114
|
10 0 12 2 14 5
|
-0.50000 12.50000 16.32483
|
| |
![]()
|
|
Перпендикулярная прямая
Элементарная геометрия
Информатика
Перпендикулярная прямая (c индивидуальным чекером)
По уравнению прямой и координатам некоторой точки (точка может быть как на прямой, так и вне ее)
определить уравнение прямой, проходящей через заданную точку и перпендикулярную заданой прямой.
Входные данные
Пять чисел - коэффициенты A, B и C уравнения прямой и координаты некоторой точки X, Y (точка может быть как на прямой, так и вне ее).
Все числа целые, по модулю не превосходят 10000.
Выходные данные
Выведите три числа - коэффициенты A, B и C уравнения прямой, перпендикулярной заданной и проходящей через заданную точку.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры
| входные данные |
выходные данные |
0 -4 8 5 0
|
-4.0 0.0 20.0
|
-4 0 8 5 0
|
0.0 4.0 0.0
|
| |
![]()
|
|
ЛА-0107_Расстояние от точки до прямой
Элементарная геометрия
Вычислительная геометрия
Расстояние от точки до прямой
Определите расстояние от точки до прямой.
Входные данные
Пять чисел – координаты точки и коэффициенты A, B и C уравнения прямой.
Все числа целые и по модулю не превосходят 10000.
Выходные данные
Одно число – расстояние от точки до прямой. Точность вычисления не менее 5 знаков.
Примеры
| входные данные |
выходные данные |
1 5 0 -4 8
|
3.0 |
1 5 -4 0 8
|
1.0
|
| |
![]()
|
|
ЛА-0107a_Расстояние от точки до прямой-2
Элементарная геометрия
Вычислительная геометрия
Расстояние от точки до прямой-2
Дана линейная функция f(x,y)=ax+by+C и точка K=(x0,y0).
Известно, что f(a,b)=D, f(x0,y0)=E.
Найдите расстояние от точки K до прямой f(x,y)=0.
Входные данные
Три числа – С (свободный член уравнения прямой и значения функци (D,E).
Все числа целые и по модулю не превосходят 109.
Выходные данные
Одно число – расстояние от точки K до прямой. Если таких значений несколько, то выведите любое.
Если задача не имеет решения, то выведите -1. Точность вычисления не менее 10-6 знаков.
Примеры
| входные данные |
выходные данные |
1 10 6
|
2 |
10 1 6
|
-1
|
| |
![]()
|
|
Точка пересечения двух прямых
Элементарная геометрия
Вычислительная геометрия
Точка пересечения прямых
На плоскости даны две прямые. Каждая прямая задается парой точек, через которые она проходит.
Требуется установить, пересекаются ли эти прямые, и найти координаты точки пересечения.
Выходные данные
Если прямые не пересекаются, выведите одно число 0. Если прямые совпадают, выведите 2.
Если прямые пересекаются ровно в одной точке, то выведите сначала число 1,
а затем два вещественных числа - координаты точки пересечения.
Координаты точки пересечения необходимо определить с точностью не менее 5 знаков.
Примеры
| входные данные |
выходные данные |
0 0 1 1
1 0 -1 2
|
1 0.50 0.50
|
1 2 3 4
0 3 4 7
|
0
|
1 2 3 4
3 4 1 2
|
2 |
| |
![]()
|
|
Перпендикулярная прямая
Элементарная геометрия
Информатика
Перпендикулярная прямая (c индивидуальным чекером)
По уравнению прямой и координатам некоторой точки (точка может быть как на прямой, так и вне ее)
определить уравнение прямой, проходящей через заданную точку и перпендикулярную заданой прямой.
Входные данные
Пять чисел - коэффициенты A, B и C уравнения прямой и координаты некоторой точки X, Y (точка может быть как на прямой, так и вне ее).
Все числа целые, по модулю не превосходят 10000.
Выходные данные
Выведите три числа - коэффициенты A, B и C уравнения прямой, перпендикулярной заданной и проходящей через заданную точку.
Числа в ответе должны быть выданы с точностью не менее 5 знаков.
Примеры
| входные данные |
выходные данные |
0 -4 8 5 0
|
-4.0 0.0 20.0
|
-4 0 8 5 0
|
0.0 4.0 0.0
|
| |
![]()
|
|
Треугольники
Элементарная геометрия
Даны два целых положительны числа \(a\) и \(b\).
Найдите количество различных целых положительных чисел \(c\), таких, что существует невырожденный треугольник с длинами сторон \(a\), \(b\) и \(c\).
Треугольник называется невырожденным, если в нем все стороны имеют положительную длину, и его площадь положительная.
Формат входных данных
На первой строке ввода находится целое число \(a\), на второй строке ввода находится целое число \(b\) (\(1 \le a, b \le 10^9\)).
Формат выходных данных
Выведите одно целое число \(k\) — количество различных целых положительных чисел \(c\), таких, что существует невырожденный треугольник с длинами сторон \(a\), \(b\) и \(c\).
| |
![]()
|
|
Поиск вершины по ортоцентру (H)
Бинарный поиск
Элементарная геометрия
Вычислительная геометрия
Точка H – центр пересечения высот треугольника (ортоцентр) АВС.
Найдите абсциссу вершины C (координату x), если известно:
- координаты точек A и B;
- координата точки D, лежащей на прямой ВС;
- точка H лежит на прямой ED (координаты точки E известны);
- для координат выполняются условия: Ax<Cx<Bx;
Входные данные: в 1-й строке вводятся значения Ax, Ay, Bx, By Dx,Dy, Ex, Ey – координаты точек A, B, D, E
Все значения целые числа в интервале [-1000;1000].
Выходные данные: ответ на задание с точностью не менее 10-5.
Пример:
| Входные данные |
Выходные данные |
| 1 1 6 3 9 1 1 5 |
2.454545 |
| 1 2 5 1 6 -1 1 5 |
3.196078 |
| |
![]()
|
|
Прямоугольники
Вычислительная геометрия
Элементарная геометрия
Петя нарисовал на клетчатом листке бумаги красивый рисунок прямоугольной формы. Его младшему брату Васе тоже захотелось порисовать, поэтому он вырезал из того же листка бумаги другой прямоугольник. При этом он не делал лишних разрезов, то есть в результате в листке осталась прямоугольная дырка. Кроме того, линии разреза не проходили (даже частично) по границам рисунка Пети. Более того, по границам рисунка не проходили даже продолжения линий разреза.
Ваша задача – по данным о расположении рисунка и прямоугольной дырки определить, испортил ли Вася рисунок старшего брата, другими словами, есть ли на вырезанном Васей прямоугольнике хотя бы маленький фрагмент рисунка Пети.
Формат входных данных
Вам даны 8 целых чисел - \(x_1, y_1, x_2, y_2, x_3, y_3, x_4, y_4\), где \((x_1, y_1)\) - координаты левого нижнего угла рисунка Пети, \((x_2, y_2)\) - координаты правого верхнего угла рисунка. Аналогично, \((x_3, y_3)\) - координаты левого нижнего угла вырезанного Васей прямоугольника, \((x_4, y_4)\) - координаты правого верхнего угла вырезанного прямоугольника. Гарантируется, что данные прямоугольники невырождены (\(x_1 < x_2\), \(y_1 < y_2\) и аналогичные неравенства для второго набора координат). Листок был не очень большим, поэтому каждое число по модулю не превосходит \(10^4\).
Формат выходных данных
Выведите YES, если Вася испортил рисунок, и NO в противном случае.
Примечание
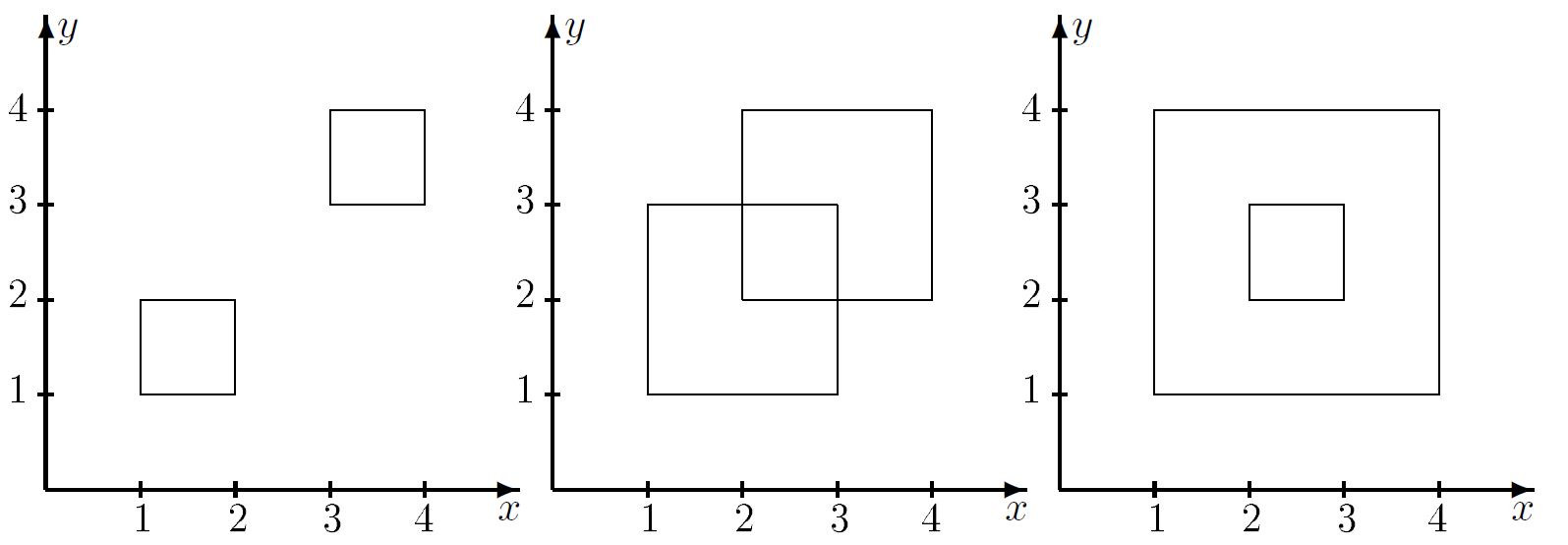
| |
![]()
|
|
Сравнение комнат
Элементарная геометрия
Маша и Петя решили выяснить, чья комната больше. Машина и Петина комнаты имеют форму прямоугольников, причем Машина комната имеет размеры \(a\) на \(b\) метров, а Петина — \(c\) на \(d\) метров.
Напишите программу, которая определит, чья комната больше: Машина или Петина.
Формат входных данных
На ввод подается четыре натуральных числа, разделенных пробелами: \(a\), \(b\), \(c\) и \(d\) (\(1 \le a, b, c, d \le 1000\)).
Формат выходных данных
Если Машина комната больше, выведите латинскую букву <<M>>. Если Петина комната больше, выведите латинскую букву <<P>>. Если комнаты ребят имеют одинаковую площадь, выведите латинскую букву <<E>>.
| |
![]()
|
|
Параллельная прямая
Элементарная геометрия
Входные данные
Четыре числа – коэффициенты A, B и C уравнения прямой и величина R.
Выходные данные
Три числа – коэффициенты A, B и C уравнения любой из прямых, параллельных заданной и лежащих от неё на расстоянии R.
| |
![]()
|
|
Принадлежность точки отрезку
Элементарная геометрия
Входные данные
Шесть чисел – координаты точки и координаты концов отрезка.
Выходные данные
Одна строка “YES”, если точка принадлежит отрезку, и “NO” в противном случае.
| |
![]()
|
|
Положение точек вне прямой
Элементарная геометрия
Входные данные
Семь чисел – координаты двух точек вне прямой и коэффициенты A, B и C её нормального уравнения.
Выходные данные
Одна строка “YES”, если точки лежат по одну сторону прямой, и “NO” в противном случае.
| |
![]()
|
|
Площадь многоугольника
Элементарная геометрия
Входные данные
В первой строке вводится одно число N (3≤N≤100000). Далее в N строках задается по паре чисел – координаты очередной вершины простого многоугольника в порядке обхода по или против часовой стрелки.
Формат выходных данных
Выходные данные
Выведите одно число – величину площади приведённого многоугольника.
| |
![]()
|
|
Целочисленные точки
Элементарная геометрия
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Входные данные
В первой строке вводится N (3≤N≤1000) – число вершин многоугольника. В последующих N строках идут координаты (Xi, Yi) вершин многоугольника в порядке обхода по часовой стрелке. Xi и Yi – целые числа, по модулю не превосходящие 106.
Выходные данные
Вывести одно число – искомое количество точек.
| |
![]()
|
|
Наиболее удаленная точка
Элементарная геометрия
Линейный поиск
Выведите координаты наиболее удаленной от начала координат точки.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n, затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Величина n не превосходит 100, все исходные координаты – целые числа, не превосходящие 103
по абсолютной величине.
Выходные данные
Выведите координаты точки, наиболее удаленной от начала координат.
| |
![]()
|
|
Центр тяжести
Элементарная геометрия
Структуры
Выведите координаты центра тяжести данного множества точек.
Создайте структуру Pointи сохраните исходные данные в массиве структур Point.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n, затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Величина n не превосходит 100, все исходные координаты – целые числа, не превосходящие 103.
Выходные данные
Выведите координаты центра тяжести данного множества точек. Ответ необходимо выводить с точностью в 15 значащих цифр.
| |
![]()
|
|
Диаметр множества
Элементарная геометрия
Структуры
Выведите диаметр данного множества – максимальное расстояние между любыми двумя точками.
Создайте структуру Point и сохраните исходные данные в массиве структур Point.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n, затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Величина n не превосходит 100, все исходные координаты – целые числа, не превосходящие 103.
Выходные данные
Необходимо вывести диаметр данного множества с точностью в 15 значащих цифр.
| |
![]()
|
|
Максимальный периметр
Элементарная геометрия
Среди исходных точек найдите три, образующие треугольник с максимальным периметром. Выведите данный периметр.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n (2<n<101), затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Все исходные координаты – целые числа, не превосходящие 103.
Выходные данные
Необходимо вывести найденный периметр с точностью в 15 значащих цифр.
| |
![]()
|
|
Максимальная площадь
Элементарная геометрия
Структуры
Среди исходных точек найдите три, образующие треугольник максимальной площади. Выведите данную площадь.
Создайте структуру Point и сохраните исходные данные в массиве структур Point.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n (2<n<101), затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Все исходные координаты – целые числа, не превосходящие 103.
Выходные данные
Необходимо вывести найденную площадь с точностью в 15 значащих цифр.
| |
![]()
|
|
Нечётный N-угольник
Элементарная геометрия
Выпуклый N-угольник P преобразуется в N-угольник Q путём замены середин сторон исходного многоугольника P на вершины многоугольника Q. Требуется по выпуклому N-угольнику Q, заданному координатами вершин, восстановить координаты вершин исходного N-угольника P.
Входные данные
Входные данные содержит нечётное число вершин N (3 <= N <= 999), за которым следуют целочисленные координаты xi yi вершин многоугольника Q, перечисленные в порядке обхода по часовой стрелке. Значения координат находятся в диапазоне от -20000 до 20000. Все числа во входном файле целые и разделены произвольным количеством пробелов и/или символов перевода строки.
Выходные данные
В выходных данных должны содержаться координаты вершин N-угольника P, перечисленные в порядке обхода по часовой стрелке. При этом первая и вторая вершина должны образовывать сторону, на которой лежит первая вершина N-угольника Q.
| |
![]()
|
|
Пеленг НЛО
Элементарная геометрия
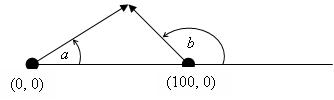
Два радара, расположенные в точках с координатами (0, 0) и (100, 0), обнаружили неопознанный объект. По таинственной причине, связанной, возможно, с внеземной природой объекта, радары оказались способны определить только направление на объект (пеленг), но не расстояние до объекта. Пеленг измеряется в градусах, против часовой стрелки, начиная от направления "на восток" (т. е. пеленг второго радара относительно первого равен 0°, пеленг первого радара относительно второго - 180°).
Требуется найти координаты НЛО или определить, что это невозможно.
Входные данные
Во входном файле содержатся вещественные числа a и b (0 <= a, b < 360), разделенные пробелами.
Выходные данные
В выходном файле должны содержаться два вещественных числа, x и y, представляющие координаты объекта с точностью до 4 знаков после запятой. Если определить координаты невозможно, следует вывести два числа 0 (нуль).
| |
![]()
|
|
Треугольная рамка
Элементарная геометрия
Картины художников-абстракционистов весьма необычны. На них часто изображены абсолютно непонятные предметы. Один известный художник-абстракционист решил добавить своим картинам оригинальности следующим способом. Вместо прямоугольных рамок, в которые обычно вставляются картины, он решил на ближайшей выставке использовать треугольные.
Однако все оказалось совсем не так просто. Художник изготовил рамку, поместил в нее картину и понял, что что-то не так. Рамка получилась слишком широкой, и картина выглядела совсем не так ярко, как он ожидал.
Немного поразмыслив, художник понял, что то, насколько рамка <<подходит>> для картины, определяется площадью рамки. Кроме этого он понял, что рамки надо не изготавливать самостоятельно, а покупать в специальном магазине. Заглянув в прайс-лист магазина, он увидел, что для каждой рамки в нем указаны длины внешних сторон и ширина.
Поясним подробнее то, как выглядит треугольная рамка. Ее изготовление происходит следующим образом: берется доска из красного дерева, имеющая форму треугольника со сторонами \(a\), \(b\) и \(c\). После этого стороны этого треугольника мысленно сдвигаются внутрь него на расстояние \(d\) (измеряемое по перпендикуляру к соответствующей стороне). На точках пересечения <<сдвинутых>> сторон строится маленький треугольник, который затем вырезается из исходного. Пример рамки со сторонами \(a=6\), \(b=8\), \(c=10\) и шириной \(d=1\) показан на рисунке.
Помогите художнику по имеющимся в прайс-листе данным вычислить площадь рамки.
Формат входных данных
Входные данные содержит четыре целых числа \(a\), \(b\), \(c\), \(d\) (\(1 \le a, b, c, d \le 1000\)) — длины внешних сторон рамки и ее ширину, соответственно. Гарантируется, что треугольник со сторонами \(a\), \(b\) и \(c\) существует, и что в треугольнике есть точка, расстояние от которой до ближайшей стороны строго больше \(d\).
Формат выходных данных
Выведите площадь рамки с точностью не меньше \(10^{-5}\).
| |
![]()
|
|
Шоссе
Способы задания графа
Использование сортировки
Элементарная геометрия
Во Флатландии \(n\) городов, расположенных в различных точках плоскости. Известно, что никакие три города не лежат на одной прямой.
Правительство решило построить в стране сеть сверхскоростных шоссе. Сеть шоссе должна быть такой, чтобы из любого города можно было проехать в любой другой по построенным шоссе. А в целях экономии средств было решено, что путь, соединяющий любые два города, должен быть единственным. Каждое шоссе представляет собой отрезок, соединяющий некоторую пару городов.
Завод, выполняющий этот госзаказ, подготовил проект сети шоссе. Проект представляет собой описание \(n - 1\) шоссе. Каждое шоссе задается городами, которые оно соединяет. В целях секретности вместо названий городов в проекте были использованы коды — числа от 1 до \(n\).
Однако когда дело дошло до реализации проекта, выяснилось, что документ, в котором было указано соответствие номеров городам, утерян. Поскольку проект приурочен к пятисотлетию культурной столицы Флатландии, переделывать проект полностью оказалось невозможно. Поэтому было решено установить некоторое новое соответствие номеров городам.
При попытке это сделать разработчики проекта столкнулись со следующей проблемой. В соответствии с техническими нормами строительства, недопустимо, чтобы шоссе пересекались вне городов. Поэтому не любое сопоставление номеров городам допустимо. После пары бессонных ночей главный инженер завода решил поручить спасение проекта вам.
Ваша задача — таким образом сопоставить числам от 1 до \(n\) города, чтобы после реализации проекта шоссе не пересекались вне городов, которые они соединяют.
Формат входных данных
В первой строке содержится целое число \(n\) — количество городов во Флатландии (\(2 \le n \le 1500\)).
Далее следует \(n\) описаний городов. Описание каждого города состоит из двух строк. Первая строка содержит название города — строку, состоящую из символов с ASCII-кодами от 33 до 127. Названия различных городов не совпадают. Длина названия города не превышает 60 символов. Вторая строка описания города содержит два целых числа \(x\) и \(y\) — координаты города. Координаты не превышают \(10^4\) по абсолютной величине.
Далее следуют \(n - 1\) строк, которые описывают проект строительства сети шоссе в его текущем состоянии. Каждая строка содержит по два целых числа — номера городов, соединенных шоссе в проекте. Никакое шоссе в проекте не соединяет город сам с собой, никакие два города не соединены более чем одним шоссе.
Формат выходных данных
Выведите \(n\) строк, \(i\)-я из этих строк должна содержать название города, который следует сопоставить числу \(i\) в проекте. Если решений несколько, выведите любое.
Если решения не существует, выведите <<No solution>>.
Иллюстрация к примеру
| |
![]()
|
|
Планета Плюк
Эвристические методы
Элементарная геометрия
На планете Плюк, поверхность которой мы будем считать абсолютно плоской, был разработан новый принцип перемещения единственного имеющегося там транспортного средства — пепелаца. А именно, на расстоянии одного километра друг от друга в точках \((0, 0)\) и \((1, 0)\) были построены две станции управления пепелацами \(A\) и \(B\). С помощью них можно мгновенно переместить любой пепелац, повернув его на 90 градусов по или против часовой стрелки относительно точки \(A\) или \(B\). Расстояние от пепелаца до соответствующей станции при этом не меняется. Следующее перемещение можно делать как относительно той же станции, так и относительно другой.
Например, если повернуть пепелац, находящийся в точке \((3, 1)\) на 90 градусов против часовой стрелки относительно станции \(A\), то он переместится в точку \((-1, 3)\), если его затем повернуть на 90 градусов по часовой стрелке относительно станции \(B\), то он переместится в точку \((4, 2)\), если затем повернуть его вокруг станции \(B\) по часовой стрелке еще раз, он переместиться в точку \((3, -3)\).
Один житель планеты недавно решил отправиться на своем пепелаце в гости к другу. Житель проживает около точки с координатами \((x_1, y_1)\), а его друг — около точки с координатами \((x_2, y_2)\). Помогите жителю с помощью станций управления пепелацем оказаться как можно ближе к месту, где проживает его друг, чтобы потом меньше было идти по пустыне.
Поскольку перемещения мгновенные и абсолютно бесплатные, то минимизировать количество перемещений не надо.
Формат входных данных
Входные данные содержит четыре целых числа — \(x_1\), \(y_1\), \(x_2\) и \(y_2\), они не превышают \(10^4\) по абсолютной величине.
Формат выходных данных
Выведите последовательность перемещений с использованием станций управления, которая перемещает пепелац из точки \((x_1, y_1)\) как можно ближе к точке \((x_2, y_2)\).
Поворот по часовой стрелке относительно станции \(A\) обозначается как <<+A>>, поворот против часовой стрелки относительно станции \(A\) обозначается как <<-A>>, соответствующие повороты относительно станции \(B\) обозначаются как <<+B>> и <<-B>>. Выводите по одному перемещению на строке.
Выведенная последовательность не обязана быть минимальной по количеству перемещений, но должна содержать не более \(10^6\) действий.
| |
![]()
|
|
Полигон
Элементарная геометрия
Бинарный поиск значения функции
Одной из первоочередных задач, стоящих перед министерством обороны Флатландии, является модернизация вооружения. В связи с этим было решено построить новый испытательный полигон.
По форме полигон представляет собой выпуклый многоугольник. Для демонстрации военных испытаний на полигоне различным чиновникам, неподалеку от него решено было построить наблюдательный центр. В результате длительных исследований было установлено, что основной характеристикой местоположения наблюдательного центра является степень этого центра относительно полигона.
Степень точки \(A\) относительно многоугольника вычисляется по следующему правилу. Рассмотрим все лучи с вершиной в точке \(A\), имеющие общие точки с многоугольником. Для каждого такого луча найдем минимальное и максимальное расстояние вдоль него от точки \(A\) до некоторой точки многоугольника: \(d_{min}\) и \(d_{max}\). Степенью точки относительно данного многоугольника назовем минимум величины \(d_{min}\times d_{max}\) по всем таким лучам.
Военные не справляются с задачей вычисления степени наблюдательного центра относительно полигона и решили подключить к этой задаче вас. Помогите им!
Будем считать, что наблюдательный центр находится в точке \((0, 0)\). Входной файл содержит описание полигона.
Формат входных данных
Первая строка содержит число \(n\) — количество вершин полигона (\(3 \le n \le 100\)). Следующие \(n\) содержат по два вещественных числа — координаты вершин полигона в порядке обхода их против часовой стрелки. Координаты не превышают \(1000\) по абсолютной величине. Гарантируется, что наблюдательный центр находится вне полигона, полигон представляет собой выпуклый невырожденный многоугольник, никакие три его последовательных вершины не лежат на одной прямой. Никакая сторона многоугольника не лежит на луче с центром в начале координат.
Формат выходных данных
Выведите одно число — степень наблюдательного центра относительно полигона. Ответ должен отличаться от правильного не более чем на \(10^{-4}\).
| |
![]()
|
|
В школу на велосипеде
Алгоритм Дейкстры
Элементарная геометрия
Петя любит ездить в школу на велосипеде. Но ездить на велосипеде по тротуарам запрещено, а ездить по дороге опасно. Поэтому Петя ездит только по специальным велосипедным дорожкам. К счастью, и Петин дом, и Петина школа находятся в непосредственной близости от таких дорожек.
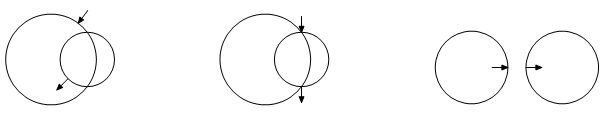
В городе, где живет Петя, есть ровно две велосипедных дорожки. Каждая дорожка имеет форму окружности. В точках их пересечения можно переехать с одной дорожки на другую.
Петя знает точку, в которой он заезжает на дорожку, и точку, в которой следует съехать, чтобы попасть в школу. Петю заинтересовал вопрос: какое минимальное расстояние ему следует проехать по дорожкам, чтобы попасть из дома в школу.
Входные данные
Будем считать, что в городе введена прямоугольная декартова система координат.
Первые две строки входных данных описывают велосипедные дорожки. Каждая из них содержит по три целых числа – координаты центра окружности, которую представляет собой соответствующая дорожка, и ее радиус. Координаты и радиус не превышают 200 по абсолютной величине, радиус – положительное число. Гарантируется, что дорожки не совпадают.
Следующие две строки содержат по два вещественных числа – координаты точки, где Петя заезжает на дорожку, и точки, в которой Петя съезжает с дорожки. Гарантируется, что каждая из точек с высокой точностью лежит на одной из дорожек (расстояние от точки до центра одной из окружностей отличается от ее радиуса не более, чем на 10-8). Точки могут лежать как на одной дорожке, так и на разных.
Выходные данные
Выведите минимальное расстояние, которое следует проехать Пете по велосипедным дорожкам, чтобы попасть из дома в школу. Ответ должен отличаться от правильного не более, чем на 10-4.
Если доехать из дома до школы по велосипедным дорожкам невозможно, выведите число -1.
| |
![]()
|
|
Точка пересечения прямых
Элементарная геометрия
На плоскости даны две прямые. Каждая прямая задается парой точек, через которые она проходит. Требуется установить, пересекаются ли эти прямые, и найти координаты точки пересечения.
Входные данные
Вводятся сначала координаты двух различных точек, через которые проходит первая прямая, а затем - координаты еще двух различных (но, быть может, совпадающих с первыми двумя) точек, через которые проходит вторая прямая. Координаты каждой точки - целые числа, по модулю не превышающие 1000.
Выходные данные
Если прямые не пересекаются, выведите одно число 0. Если прямые совпадают, выведите 2. Если прямые пересекаются ровно в одной точке, то выведите сначала число 1, а затем два вещественных числа - координаты точки пересечения.
| |
![]()
|
|
Перпендикулярная прямая
Элементарная геометрия
Входные данные
Пять чисел - коэффициенты A, B и C уравнения прямой и координаты некоторой точки X, Y (точка может быть как на прямой, так и вне ее). Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите три числа - коэффициенты A, B и C уравнения прямой, перпендикулярной заданной и проходящей через заданную точку. Числа в ответе должны быть выданы с точностью не менее 5 знаков после десятичной точки.
| |
![]()
|
|
Точка пересечения высот
Элементарная геометрия
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа: X и Y, задающие координаты точки пересечения высот в треугольнике, образованном исходными точками. Числа в ответе должны быть выданы с точностью не менее 5 знаков после десятичной точки.
| |
![]()
|
|
Точка пересечения медиан
Элементарная геометрия
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа X, Y, задающие координаты точки пересечения медиан в треугольнике, образованном исходными точками. Числа в ответе должны быть выданы с точностью не менее 5 знаков после десятичной точки.
| |
![]()
|
|
Точка пересечения биссектрис
Элементарная геометрия
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите два числа X, Y, задающие координаты точки пересечения биссектрис в треугольнике, образованном исходными точками. Числа в ответе должны быть выданы с точностью не менее 5 знаков после десятичной точки.
| |
![]()
|
|
Вписанная окружность
Элементарная геометрия
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите три числа: X, Y, R, задающие координаты центра и радиус окружности, вписанной в треугольник, образованный данными точками. Числа в ответе должны быть выданы с точностью не менее 5 знаков после десятичной точки.
| |
![]()
|
|
Описанная окружность
Элементарная геометрия
Входные данные
Даны координаты трех точек, не лежащих на одной прямой: X1, Y1, X2, Y2, X3, Y3. Все числа целые, по модулю не превосходят 1000.
Выходные данные
Выведите три числа X, Y, R, задающие координаты центра и радиус окружности, описанной вокруг треугольника, образованного данными точками. Числа в ответе должны быть выданы с точностью не менее 5 знаков после десятичной точки.
| |
![]()
|
|
Площадь треугольника
Вычислительная геометрия
Элементарная геометрия
Входные данные
Шесть чисел – координаты трёх вершин треугольника.
Выходные данные
Одно число – величина площади треугольника.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1 2 4 3 2 |
2.50000 |
| |
![]()
|
|
Угол между векторами
Элементарная геометрия
Входные данные
Четыре числа – координаты двух невырожденных (т.е. ненулевых) векторов.
Выходные данные
Одно число – величина угла α
между векторами (0≤α≤π) с точностью до пятого знака после запятой.
| |
![]()
|
|
Полярное расстояние
Элементарная геометрия
Заданы полярные координаты двух точек на плоскости. Требуется найти расстояние между этими точками.
Входные данные
Вводятся 4 числа, первые два задают радиус и полярный угол первой точки, последние два - второй. Обратите внимание: все углы задаются в градусах.
Выходные данные
Выведите расстояние между точками не меньше, чем с 3 знаками после десятичной точки.
| |
![]()
|
|
Преобразование системы координат
Элементарная геометрия
Есть две системы координат - первая и вторая. Вторая система устроена так, что ее центр в первой системе имеет координаты (A,B). Ее оси параллельны осям первой системы. При этом точка, которая во второй системе имеет координаты (1,0) в первой имеет координаты (C,B), а точка, имеющая во второй координаты (0,1) - координаты (A,D).
Дана точка, которая в первой системе имеет координаты X1,Y1.
Какие координаты она будет иметь во второй системе?
Какие координаты будет иметь точка в первой системе, если ее координаты во второй - X2, Y2?
Входные данные
Даны вещественные числа A, B, C, D, X1, Y1, X2, Y2.
Выходные данные
Выведите координаты первой точки во второй системе и координаты второй точки - в первой. Все числа должны быть выведены не менее, чем с 3 знаками после десятичной точки.
| |
![]()
|
|
Неподвижная точка карты
Элементарная геометрия
Первый учебный день шестиклассника Пети начался с урока географии. Учитель объяснял классу, что перед тем, как изучать просторы нашей Родины, нужно научиться пользоваться географическими картами. Было также упомянуто и о том, что такое масштаб карты. В качестве домашней работы Пете и его одноклассникам задали нарисовать план (карту) своей комнаты, соблюдая масштабирование. Петю очень заинтересовало задание учителя, и поэтому, как только он пришел из школы домой, он принялся рисовать план. Это занятие было очень увлекательным, но вскоре с работы пришла Петина мама, сказала, что здоровье превыше всего и позвала его обедать. Во время обеда она по пути на кухню зашла в Петину комнату и решила, что ее надо проветрить. Для этого она открыла окно, перед которым стоял Петин стол.
Насытив свой желудок, Петя вернулся в комнату и обнаружил, что его творение сдуло ветром на пол. Сначала он обеспокоился тем, в порядке ли рисунок, но удостоверившись, что все нормально, не стал спешить и поднимать план с пола. Он вспомнил слова учителя географии, который в конце урока поведал им некое нетривиальное утверждение и предложил любопытным проверить его на досуге.
Утверждение гласило: "если взять две карты одной и той же области, сделанные с разным масштабом, и расположить меньшую поверх большей так, что меньшая карта окажется строго внутри большей, то можно найти такую точку (она называется "неподвижная точка"), что то, что изображено в этой точке на обеих картах соответствует одной и той же точке местности". Петя заметил, что пол комнаты можно считать картой комнаты (масштаб 1:1). Он решил найти неподвижную точку для лежащего на полу нарисованного им плана и пола. Но Петя не сумел сделать это самостоятельно, поэтому он обратился к вам за помощью.
Входные данные
Комната Пети и ее план имеют форму прямоугольника. Первая строка содержит два вещественных числа: ширину X и длину Y комнаты Пети (1≤X≤1000, 1≤Y≤1000). Комната расположена в декартовой прямоугольной системе координат так, что углы комнаты расположены в точках с координатами (0,0), (X,0), (X,Y), (0,Y).
Вторая строка содержит восемь вещественных чисел, описывающих положение углов плана комнаты в той же самой системе координат. Сначала задаются координаты того угла плана, который соответствует углу комнаты с координатами (0,0), затем — (X,0), (X,Y), наконец, (0,Y). Гарантируется, что входные данные корректны, то есть план является прямоугольником, линейные размеры плана находятся в полном соответствии с линейными размерами комнаты, план не выходит за границы комнаты.
Все числа заданы с точностью 5 знаков после десятичной точки. План выполнен в масштабе не менее 0.0001 и не более 1. Масштаб не может быть равен 1. Карта расположена лицевой стороной вверх.
Выходные данные
В первую строку выведите 2 вещественных числа — координаты неподвижной точки плана и пола. Ответ нужно выдать с 3 знаками после десятичной точки.
| |
![]()
|
|
Найди прямую
Элементарная геометрия
На плоскости дано множество отрезков. Требуется найти прямую, которая пересекла бы наибольшее возможное количество из данных отрезков и при этом проходила бы как минимум через две точки с целочисленными координатами.
Считается, что прямая пересекает отрезок, если она имеет с ним хотя бы одну общую точку (т.е. она может проходить через конец отрезка, внутреннюю точку отрезка, либо содержать весь отрезок).
Формат входных данных
Сначала вводится число N — количество отрезков (1≤N≤1000). Далее идет N четверок чисел Xi1, Yi1, Xi2, Yi2 задающих координаты концов отрезков. Все эти числа целые, по модулю не превосходящие 10000.
Заданные отрезки могут пересекаться, иметь общие части, один из них может полностью содержаться внутри другого. Отрезки имеют ненулевую длину.
Формат выходных данных
Выведите координаты каких-нибудь двух точек, через которые проходит прямая, пересекающая наибольшее количество отрезков. Координаты точек должны быть целыми и не должны по модулю превышать 107.
| |
![]()
|
|
Формула - 3
Обход в глубину
Сканирующая прямая
Элементарная геометрия
В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.
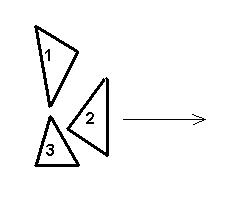
Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.
Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).
Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).
Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).
Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.
Входные данные
В первой строке вводится натуральное число N( 1 ≤ N ≤ 30 000).
В каждой из следующих N строк содержится по 6 чисел: x1, y1, x2, y2, x3, y3 – координаты трех вершин скутера на старте, целые числа, не превосходящие по модулю 106. В начальный момент скутеры не задевают друг друга.
Выходные данные
Выведите через пробел N чисел – номера скутеров в том порядке, в котором они могут стартовать. Если решений несколько, выведите одно любое из них. Если решений нет, выведите одно число -1.
Примечание
Первый тест соответствует приведенному рисунку. Ответ 2 3 1 в этом тесте также является правильным
| |
![]()
|
|
Точки
Элементарная геометрия
Петя и Вася играют в "точки". Петя отметил на клетчатом листе бумаги несколько точек – узлов сетки. Вася хочет окружить их многоугольником так, чтобы все отмеченные узлы лежали строго внутри (не на границе) этого многоугольника и чтобы все стороны этого многоугольника проходили только по сторонам или диагоналям клеток сетки, а его периметр был минимально возможным. Определите, чему равен периметр такого многоугольника.
Входные данные
В первой строке входных данных содержится число N – количество отмеченных Петей точек (1 ≤ N ≤ 100 000).
В каждой из следующих N строк записаны по два числа xi, yi – координаты точек, нарисованных Петей. Координаты по абсолютной величине не превосходят 106. Некоторые точки могут совпадать.
Выходные данные
Требуется вывести одно число – периметр искомого многоугольника. Ответ нужно вывести с точностью не менее 0.001.
| |
![]()
|
|
Свет
Алгоритм Дейкстры
Элементарная геометрия
В точке (0, 0) координатной плоскости расположена лампочка, которая представляет собой точечный источник света. Неподалеку от лампочки находится дом Пети, который представляет собой выпуклый многоугольник с N вершинами. Сам Петя находится в точке с координатами (x, y).
Петя хочет увидеть свет. Для этого ему необходимо оказаться в такое точке, что отрезок, соединяющей ее с началом координат, не пересекается с домом Пети (но может его касаться, в частности, проходить вдоль стороны многоугольника дома).
Петя может перемещаться по плоскости со скоростью v. Разумеется, Петя не может проходить сквозь дом (хотя он может двигаться по его границе).
Выясните, какое минимальное время требуется Пете, чтобы оказаться в освещенной точке.
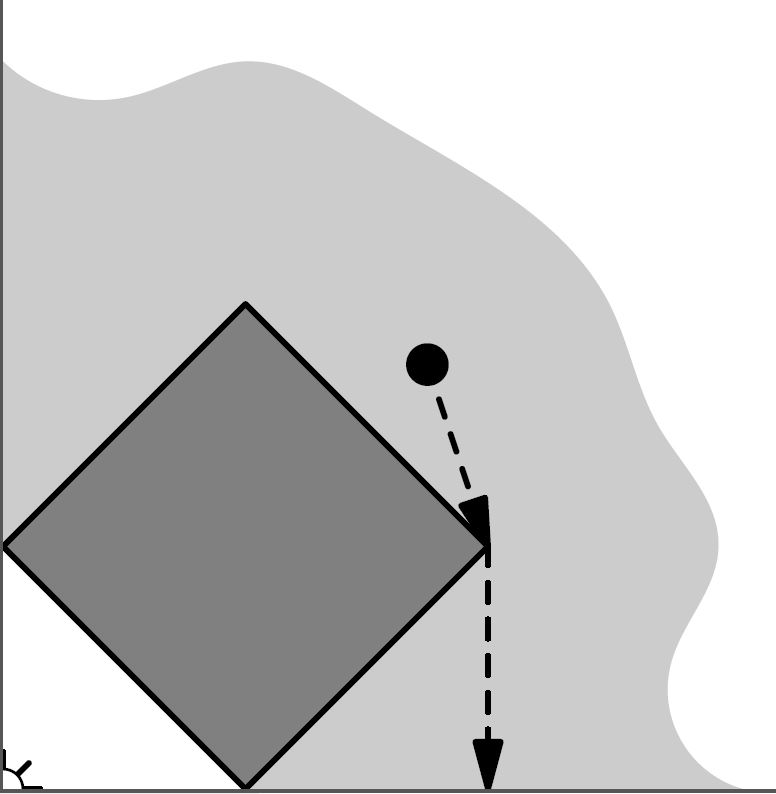
Входные данные
В первой строке вводятся координаты Пети – два неотрицательных вещественных числа, не превышающих 1000, и его скорость v – вещественное число, 10-2≤ v≤ 104.
Вторая строка содержит N – число вершин в многоугольнике, задающем Петин дом ( 3≤N≤100). Далее в N строках вводится по два вещественных числа – координаты вершин многоугольника в порядке их обхода против часовой стрелки. Все координаты неотрицательны и не превышают 1000.
Гарантируется, что входные данные корректны, в частности, многоугольник выпуклый, и никакие три его последовательные вершины не лежат на одной прямой. Также гарантируется, что и Петя, и лампочка находятся снаружи от многоугольника, в частности, не находятся на его границе. Расстояние от точки, где находится Петя, до многоугольника и от начала координат до многоугольника не меньше 10-2, расстояние от Пети до начала координат не меньше 10-2.
Выходные данные
Выведите минимальное время, за которое Петя сможет попасть в освещенную точку. Ваш ответ должен отличаться от правильного не более чем на 10-4.
| |
![]()
|
|
Триангуляция Делоне
Элементарная геометрия
Триангуляцией некоторого набора точек на плоскости называется набор невырожденных треугольников, удовлетворяющий следующим свойствам:
1) Вершинами треугольников являются только точки исходного набора. Каждая точка исходного набора является вершиной хотя бы одного треугольника.
2) Два различных треугольника либо не имеют общих точек, либо имеют общую вершину, либо имеют общую сторону (но площадь их пересечения всегда равна 0).
3) Любая точка, лежащая внутри выпуклой оболочки исходного набора точек, принадлежит хотя бы одному треугольнику (она может принадлежать нескольким треугольникам, если является их общей вершиной или принадлежит их общей стороне). (Выпуклой оболочкой некоторого набора точек называется наименьший выпуклый многоугольник, содержащий все эти точки).
Триангуляция называется триангуляцией Делоне, если кроме того для нее выполняется следующее условие:
4) Внутри окружности, описанной около любого треугольника из триангуляции, не лежит ни одна из исходных точек (точки могут лежать на окружности, в частности на ней, очевидно, лежат вершины рассматриваемого треугольника).
Для заданного набора точек найдите количество его триангуляций Делоне (две триангуляции считаются различными, если они отличаются хотя бы одним треугольником).
Входные данные
В первой строке вводится число N - количество точек (3 <= N <= 30) исходного набора. Следующие N строк содержат по одной паре вещественных чисел - координаты соответствующей точки. Никакие три точки не лежат на одной прямой.
Выходные данные
Выведите количество различных триангуляций Делоне указанного набора точек.
| |
![]()
|
|
Фонтан
Квадродерево
Бинарный поиск по ответу
Элементарная геометрия
Администрация одного института решила построить в холле фонтан. По плану администрации, фонтан должен иметь форму круга с максимально возможным радиусом. Дизайнеру сообщили, что холл института имеет вид прямоугольника, размером X×Y метров. Однако когда дизайнер стал выбирать место для фонтана, он столкнулся с серьезной проблемой: в холле института обнаружилось N круглых колонн, снести которые не представляется возможным.
Таким образом, у него появилась проблема: где следует поместить фонтан, чтобы он имел максимально возможный радиус и не имел ненулевого по площади пересечения с колоннами. Вам предстоит помочь ему в решении этой нелегкой задачи.
Входные данные
В первой строке входных данных содержатся вещественные числа X и Y, 1 <= X, Y <= 104 . Будем считать, что прямоугольник холла расположен на координатной сетке так, что его углы имеют координаты (0, 0), (X, 0), (X, Y) и (0, Y).
Во второй строке задается число N (0 <= N <= 10) - количество колонн. Следующие N строк содержат параметры колонн - i-я строка содержит три вещественных числа Xi, Yi и Ri - координаты центра и радиус i-й колонны (Ri <= Xi <= X-Ri, Ri <= Yi <= Y-Ri, 0.1 <= Ri <= min(X / 2, Y / 2); для любых i ≠ j sqrt( (Xi - Xj)2 + (Yi - Yj)2 )>= Ri + Rj). Все вводимые числа разделены пробелами.
Выходные данные
Выведите три вещественных числа: XF, YF и RF - координаты центра и радиус фонтана. Фонтан должен быть полностью расположен внутри холла (допускается касание стен) и не иметь ненулевого пересечения ни с одной из колонн (допускается касание). Радиус фонтана должен быть максимален. Разделяйте числа пробелами и/или переводами строки. Если решений несколько, выведите любое из них.
| |
![]()
|
|
Треугольник и точка
Элементарная геометрия
В декартовой системе координат на плоскости заданы координаты вершин треугольника и ещё одной точки. Определить, принадлежит ли эта точка треугольнику.
Входные данные
В четырёх строках находятся пары чисел - координаты точек. Числа в первых трёх строках - это координаты вершин треугольника, в четвёртой строке - координаты тестируемой точки. Координаты вершин - целые числа, для любой точки выполняются следующие условия: -10 000 <= x, y <= 10 000.
Выходные данные
Вывести слово "In", если точка находится внутри треугольника, или "Out" - если снаружи.
| |
![]()
|
|
Пересечение отрезков
Элементарная геометрия
Два отрезка на плоскости заданы целочисленными координатами своих концов в декартовой системе координат. Требуется определить, существует ли у них общая точка.
Входные данные
В первой строке содержатся координаты первого конца первого отрезка, во второй - второго конца первого отрезка, в третьей и четвёртой - координаты концов второго отрезка. Kоординаты целые и по модулю не превосходят 10 000.
Выходные данные
Выводится слово "Yes", если общая точка есть, или слово "No" - в противном случае.
| |
![]()
|
|
Открытка и конверт
Элементарная геометрия
Даны размеры прямоугольных открытки и конверта. Требуется определить, поместится ли открытка в конверт.
Входные данные
В первой строке находятся размеры открытки, во второй - размеры конверта. Pазмеры открытки и конверта - целые положительные числа, не превосходящие 100.
Выходные данные
Если открытку можно вложить в конверт, вывести "Possible", если нет - вывести "Impossible".
| |
![]()
|
|
Прямая и квадраты
Элементарная геометрия
В прямоугольной декартовой системе координат прямая задана двумя принадлежащими ей точками (0, W) и (100N, E). Также заданы N2 квадратов со сторонами, параллельными осям координат. Квадрат Si, j имеет координаты углов (100i, 100j) и (100i - 100, 100j - 100), i, j = 1, 2, ..., N. Требуется найти количество квадратов, имеющих общую точку с прямой.
Входные данные
В первой строке находятся три целых числа, N, W и E, разделённых пробелами. 1 <= N <= 100, 0 <= W, E <= 100N, все числа целые.
Выходные данные
Вывести одно число - количество квадратов.
| |
![]()
|
|
Прямоугольное деление
Элементарная геометрия
Обход в ширину
Дано N прямоугольников со сторонами, параллельными осям координат. Требуется определить, на сколько частей эти прямоугольники разбивают плоскость (внутри частей не должно быть границ прямоугольников).
Входные данные
В первой строке содержится число прямоугольников N. Далее идут N строк, содержащих по 4 числа x1, y1, x2, y2 - координаты двух противоположных углов прямоугольника.
Ограничения: 1 <= N <= 100, координаты представляют собой целые числа и по абсолютной величине не превосходят 10 000.
Выходные данные
Вывести одно число - количество частей, на которые разбивается плоскость.
| |
![]()
|
|
Круговая площадь
Элементарная геометрия
Два круга заданы координатами центров в прямоугольной декартовой системе координат и радиусами. Найти площадь их пересечения.

Ограничения: во входных данных числа вещественные и по модулю не превосходят 1000.
Входные данные
В первой строке находятся шесть вещественных чисел через пробел - координаты центров и радиусы двух кругов: x1, y1, r1, x2, y2, r2.
Выходные данные
Вывести одно вещественное число с двумя знаками после запятой - площадь пересечения кругов.
| |
![]()
|
|
Площадь треугольника
Элементарная геометрия
Даны длины трёх отрезков. Если возможно, требуется построить треугольник, в котором один из этих отрезков был бы высотой, один - биссектрисой и один - медианой; все построенные из одной вершины.
Ограничения: длина каждого из трёх отрезков от 0.01 до 100, точность результата должна быть 0.001.
Входные данные
Вводятся три положительных числа, разделённых пробелами, - длины отрезков.
Выходные данные
Выводится одно число - площадь треугольника. Если треугольник нельзя построить, вывести -1. Если может быть построено несколько треугольников с разными площадями, вывести 0.
| |
![]()
|
|
Морской бой
Элементарная геометрия
Бинарный поиск по ответу
N вражеских кораблей движутся прямолинейно с постоянными скоростями. Вакуумная бомба уничтожает все объекты в радиусе R от точки взрыва (то есть все объекты, расстояние от которых до точки взрыва не больше R). Взрывать бомбу можно только в целые моменты времени.
Требуется определить, за какое наименьшее количество взрывов можно уничтожить все корабли, а также в какие моменты времени и в каких точках для этого следует произвести взрывы. Время отсчитывается от момента, когда координаты движущихся кораблей были определены со спутника.
Входные данные
В первой строке входных данных задаются целые числа N (2 <= N <= 10) и R (0 < R ≤ 50. В следующих Nстроках содержится по 4 числа, описывающих движение кораблей. Первые два числа строки – координаты корабля в момент времени 0, по модулю не превосходящие 105. Следующие два числа – значения координат вектора скорости, по модулю не превосходящие 1000. Все эти числа целые.
Гарантируется, что никакие 2 корабля не имеют одинаковые векторы скорости.Однако вполне возможно, что в какой-то момент времени два корабля пройдут через одну точку.
Выходные данные
В первой строке выведите одно число – минимальное количество взрывов K. В следующих K строках для каждого взрыва выведите по три числа: целое время взрыва и вещественные координаты взрыва, указанные с точностью не менее трех значащих цифр после точки. Разрешается производить взрывы как в разные, так и в один и тот же момент времени. Разрешается взрывы производить как в различных точках, так и в одной точке в разные моменты времени.
Если решений несколько, выведите любое из них.
| |
![]()
|
|
Треугольники
Элементарная геометрия
На плоскости отмечено несколько точек. Требуется определить, можно ли нарисовать треугольник с вершинами в трех из этих точек, внутри которого не будет других отмеченных точек.
Входные данные
Сначала вводится натуральное число N, не превосходящее 100 – количество точек. Далее вводится N пар координат этих точек – целые числа, не превосходяшие 1000.
Выходные данные
Вывести слово YES (заглавными латинскими буквами), если такой треугольник нарисовать можно и NO в противном случае.
| |
![]()
|
|
Путь через горы
Элементарная геометрия
Динамическое программирование: два параметра
Поверхность Земли в горной местности можно представить в виде ломаной линии. Вершины ломаной расположены в точках (x1, y1), (x2, y2),…,(xN, yN), при этом xi<xi+1.
Обычный горный маг находится в точке (x1, y1) и хочет попасть в точку (xN, yN). При этом он может перемещаться только пешком. Он может ходить по поверхности Земли (т.е. вдоль ломаной). А может сотворить в воздухе мост и пройти по нему. Мост может соединять две вершины ломаной: мост не может начинаться и заканчиваться не в вершине ломаной, и мост не может проходить под землей (в том числе не может быть туннелем в горе), но мост может каким-то своим участком проходить по поверхности земли. Длина моста не может быть больше R. Суммарно маг может построить не более K мостов.
Какое наименьшее расстояние придется пройти магу, чтобы оказаться в точке (xN, yN).
Входные данные
Вводится сначала натуральное число N (2≤N≤100). Затем водится натуральное число K (1≤K≤100) — максимальное количество мостов. Далее вводится целое число R (0≤R≤10000) — максимальная возможная длина моста. Далее вводятся координаты (x1, y1), (x2, y2),…,(xN, yN). Все координаты – целые числа, не превышающие по модулю 10000, для всех i от 1 до N–1: xi<xi+1.
Выходные данные
Выведите одно число — минимальную длину пути, которую придется пройти магу (как по земле, так и по мостам). Ответ выведите не менее чем с 5 цифрами после десятичной точки.
| |
![]()
|
|
Электрик-ковбой Джо
Бинарный поиск по ответу
Элементарная геометрия
Джо - электрик-ковбой. Как у всех ковбоев у него есть лассо, как всем электрикам ему иногда приходиться залезать на столбы, и как все он ленив.
Вот и сейчас ему поручили проверить два стоящих на расстоянии d друг от друга столба высоты h1 и h2 соответственно. Чтобы убедиться, что все хорошо, Джо должен побывать на вершинах обоих столбов.
Электрик-ковбой посещает столбы следующим образом: сначала он выбирает один из столбов и просто взбирается на него. Выполнив все работы на вершине, он спускается по этому столбу на некоторую высоту (возможно до самой земли), достает свое лассо и цепляется им за некоторую точку второго столба (это может быть произвольная точка). После этого Джо прыгает и двигается вниз по дуге окружности с центром в точке, за которую зацепилось лассо, пока не достигнет либо другого столба, либо земли.
При этом если от начальной позиции электрика до конца его полета высота изменяется более чем на l, то ковбой набирает слишком большую скорость, больно ударяется и попадает в больницу, так и не выполнив работу. Поэтому Джо всегда аккуратно выбирает параметры прыжка.
Если в результате прыжка Джо оказался на земле, он подходит к другому столбу и взбирается на него. Если же Джо оказался на столбе, то он взбирается на вершину из той точки, в которой он оказался.
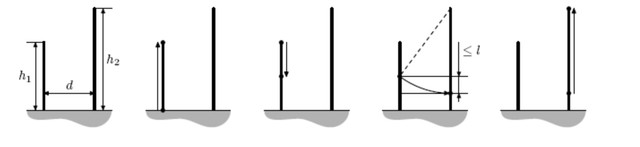
Джо просит вас помочь ему выполнить работу, сообщив какое минимальное расстояние ему придется лезть вверх по столбам.
Входные данные
Входной файл содержит четыре положительных целых числа: d, h1, h2 и l - расстояние между столбами, высоту первого и второго столбов и максимальный допустимый перепад высот при прыжке, соответственно. Все числа во входном файле не превышают 106.
Выходные данные
Выведите ответ с максимальной возможной точностью. Ответ будет проверяться с точностью до 10−5.
| |
![]()
|
|
Рисование
Элементарная геометрия
Дано N точек на плоскости, их надо покрасить в черный и белый цвета.
При этом должны присутствовать точки обоих цветов и должна существовать прямая, по одну сторону от которой все точки черные, по другую белые.
Требуется посчитать количество раскрасок, удовлетворяющих этим условиям.
Входные данные
В первой строке задано число 2≤N≤300. В следующих N строках заданы координаты точек.
Выходные данные
Выведите единственное число - количество различных раскрасок.
| |
![]()
|
|
Сад пчел
Обход в глубину
Элементарная геометрия
В саду Бена расположено n ульев. Некоторые из них соединены друг с другом или с домом Бена прямыми дорожками. Бен гуляет только по дорожкам, переходя с одной на другую только возле очередного улья. Ни дом Бена, ни какой-либо улей не расположены на дорожке, соединяющей другие два улья. Дорожки организованы таким образом, что Бен может дойти от дома до любого улья только единственным способом.
Каждую неделю Бен делает обход ульев. Он начинает от своего дома и идет по дорожкам, посещая каждый улей по крайней мере один раз, минимизируя при этом общий путь. Сын Бена решил помочь своему стареющему отцу и проложить еще одну прямую дорожку между двумя ульями, так чтобы путь Бена от дома через все ульи с возвращением к дому стал как можно короче. Она, как и старые дорожки, проходить мимо дома или другого улья не должна.
Входные данные
На вход сначала подается число n — количество ульев (1≤n≤200).
Введем координаты так, что дом Бена будет располагаться в точке (0, 0). В следующих n строках входных данных записаны координаты ульев в саду Бена. Они не превосходят 10000 по абсолютному значению. Никакие два улья не совпадают, и нет ульев, расположенных в точке (0, 0). Будем считать, что они пронумерованы от 1 до n.
Следующие n строк описывают дорожки — каждая дорожка описывается номерами объектов, которые она соединяет. Дом Бена имеет номер 0.
Выходные данные
Выведите два числа — номера объектов, которые надо соединить дополнительной дорожкой. Если требуемой прямой дорожки, сокращающей общий путь Бена не существует, то выведите –1.
| |
![]()
|
|
Подсчёт зелёных насаждений
Элементарная геометрия
В рамках проекта по улучшению городской инфраструктуры вам необходимо провести анализ распределения зеленых насаждений (деревьев, кустарников и т.д.) вокруг новых жилых комплексов. Область вокруг жилых комплексов на плане города ограничена окружностью. Внутрь одной области, ограниченной окружностью, могут попадать несколько жилых комплексов.
У вас есть массив points, где points[i] = [xi, yi] — координаты i-го зеленого насаждения на двумерной карте города.
Также у вас есть массив queries, где queries[j] = [xj, yj, rj] описывает j-ю круговую зоны, в которой необходимо оценить количество зеленых насаждений.
Для каждого запроса queries[j] вычислите количество зеленых насаждений, находящихся внутри j-й круговой зоны. Точки, находящиеся на границе зоны, также считаются входящими в эту зону.
Верните массив answer, где answer[j] — это количество зеленых насаждений в j-й круговой зоне.
| |
![]()
|
|
Собъем воздушный шарик
Элементарная геометрия
 Винни Пух и Пятачок отправились воровать мед у пчел, и, в очередной раз влипли в неприятности. Пятачку опять потребовалось выстрелить из своего охотничьего ружья и пробить воздушный шарик, на котором Винни Пух поднялся к дуплу за медом. При этом желательно попасть именно в шарик, не задев медведя. Вычислите оптимальную позицию для стрельбы. Винни Пух и Пятачок отправились воровать мед у пчел, и, в очередной раз влипли в неприятности. Пятачку опять потребовалось выстрелить из своего охотничьего ружья и пробить воздушный шарик, на котором Винни Пух поднялся к дуплу за медом. При этом желательно попасть именно в шарик, не задев медведя. Вычислите оптимальную позицию для стрельбы.
Поскольку Винни Пух очень любит покушать, то в данной задаче (да и не только в задаче) примем его за сферу радиуса P. Центр медведя находится на высоте Hp над уровнем земли. Строго над медведем , находится еще одна сфера, радиуса S – воздушный шарик; центр шарика находится на высоте Hs над уровнем земли. Центры обеих сфер находятся на одной вертикальной прямой. По понятным причинам гарантируется, что сферы не пересекаются J, однако могут касаться.
Считая, что ружье стреляет строго по прямой, вычислите минимальное расстояние L, на которое Пятачок должен отойти от места взлета, чтобы успешно поразить шарик. Шарик считается пораженным, если траектория пули хотя бы касается его поверхности; при этом если траектория пули касается медведя, то он считается невредимым.
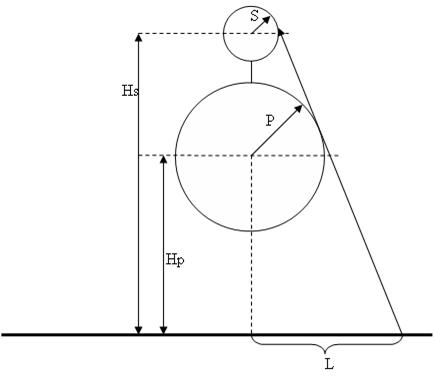
Формат входных данных
C клавиатуры вводятся положительные целые числа P, Hp, S и Hs, не превосходящие 10000.
Формат входных данных
Выведите минимальное расстояние от точки взлета, с которого можно поразить шарик из ружья с точностью не менее 5 знаков после запятой.
| |
![]()
|
|
Отражение точки
Элементарная геометрия
Заданы коэффициенты уравнения прямой ax + by + c = 0 и координаты точки A (xa, ya). Найдите точку B, которая является отражением точки A относительно заданной прямой.
Формат входных данных
В начале с клавиатуры вводятся коэффициенты уравнения прямой a, b, c, затем координаты точки A. Исходные данные являются целыми числами, по модулю не превышающими 1000
Формат выходных данных
Выведите координаты точки B с точностью до пятого знака после запятой.
| |
![]()
|
|
Сократи векторы
Элементарная геометрия
На плоскости задано N векторов – направленных отрезков, для каждого из которых известны координаты начала и конца (вектор, у которого начало и конец совпадают, называется нуль-вектором, можно считать, что нуль-вектор лежит на любой прямой, которая через него проходит). Введем следующие три операции над направленными отрезками на плоскости:
1) Направленные отрезки ненулевой длины, лежащие на пересекающихся прямых, можно заменить на их сумму, причем единственным образом. В этом случае отрезки переносятся вдоль своих прямых так, чтобы их начала совпадали с точкой пересечения прямых, и складываются по правилу сложения векторов (правилу параллелограмма, при этом началом результирующего вектора является точка пересечения прямых).
2) Направленные отрезки, лежащие на одной прямой, также можно заменить на их сумму. Для этого один из отрезков (любой) нужно перенести в начало второго из них и сложить по правилу сложения векторов на прямой:
Это правило применимо и в случае, когда один из векторов, или даже оба, являются нуль-векторами.
Заметим, что если складываемые векторы противоположно направлены и имеют одну и ту же длину, то результатом их сложения является нуль вектор.
3) В любой точке плоскости можно породить два противоположно направленных отрезка равной (в том числе и нулевой) длины:
Будем говорить, что две системы векторов эквивалентны, если от одной системы можно перейти к другой с помощью конечной последовательности перечисленных выше операций.
Требуется получить любую систему векторов, эквивалентную заданной, состоящую из как можно меньшего числа векторов.
Входные данные
В первой строке записано число N – количество заданных векторов (1 < N ≤ 1000). В каждой из следующих N строк через пробел записаны четыре числа, обозначающие координаты начала и конца каждого из векторов соответственно. Все координаты – целые числа, по модулю не превосходящие 1000.
Выходные данные
В первой строке следует записать число M – количество векторов в полученной системе (1 ≤ M ≤ N). В каждой из следующих M строк через пробел должны находиться четыре числа, обозначающие координаты начала и конца каждого из векторов соответственно. Все координаты – вещественные числа, записанные с 6 цифрами после точки.
| |
![]()
|
|
Мышка с колесиком
Элементарная геометрия
Пользователь просматривает таблицу в Internet Explorer и пользуется для прокрутки изображения колесиком на мышке. При этом все изображение сдвигается вверх или вниз на T пикселов. Пользователю очень не нравится, когда курсор мыши оказывается на горизонтальных линиях, разделяющих строки таблицы. Поэтому он хочет выбрать такое положение для курсора мыши на экране, чтобы в процессе прокрутки до конца таблицы курсор как можно меньшее число раз пересекался с линиями таблицы.
При этом если в каком-то положении курсор оказывается на двух линиях таблицы, то это считается за два пересечения курсора с линиями таблицы. Если какую-то линию курсор мыши пересекает в двух положениях (то есть, например, высота курсора 10 пикселей, а при прокрутке таблица сдвигается на 7 пикселей, тогда курсор мыши может оказываться на одной линии в двух состояниях прокрутки), то это также считается за два пересечения.
Экран монитора имеет разрешение по вертикали U пикселей. Координаты введены так, что самые верхние точки экрана имеют координату 0, а нижние — координату U–1.
Курсор мыши имеет высоту H пикселов. Расположением курсора считается самая верхняя точка курсора. Таким образом, если мы говорим, что он расположен, например, в точке с координатами 0 на экране, то его изображение расположено в точках с координатами от 0 до H–1. Курсор мыши всегда целиком помещается на экране, то есть допустимыми координатами для его расположения являются координаты от 0 до U–H.>
Таблица, которую просматривает пользователь, имеет высоту L пикселов и состоит из N–1 строки, и, следовательно, в ней N горизонтальных линий, которые имеют координаты X1, X2, …, XN. При этом 0=X1<X2<X3<…<XN=L–1.
В начальный момент времени таблица расположена так, что линия, имеющая координату 0 в таблице отображается в 0-й строке пикселов монитора. Далее при прокрутке таблица каждый раз сдвигается на T пикселов (то есть в 0-й строке монитора оказывается строка пикселов, имеющая в таблице координату T, координату 2T и т.д.). Так происходит до тех пор, пока на экране не окажется нижняя линия таблицы (которая имеет координату XN). После этого дальнейшая прокрутка не происходит (если изначально XN<U, то прокрутка вообще не происходит).
Входные данные
Во входном файле задано сначала разрешение монитора по вертикали U, затем высота курсора мыши H, затем шаг прокрутки T. Далее задана высота таблицы L. Далее задано количество разделительных линий в таблице N, и координаты X1, X2,…,XN, где расположены эти линии относительно начала таблицы.
Ограничения
- 10<U<512
- 1<H<U
- 1<T<U
- 2<N<200000
- 0=X1<X2<…<XN=L–1≤109.
Выходные данные
В выходной файл выведите сначала координату, в которой нужно расположить курсор мыши, а затем количество пересечений курсора мыши с линиями таблицы. В случае, если существует несколько начальных положений курсора мыши, выведите любое из них.
| |
![]()
|
|
Дремучий лес - 2
Многоугольники. Выпуклые оболочки
Элементарная геометрия
Будем говорить, что для наблюдателя лес является дремучим, если из своего текущего положения наблюдатель видит только деревья. Вам дана карта леса и координаты точки, в которой находится наблюдатель. Требуется определить, кажется ли лес дремучим данному наблюдателю.
На карте леса все деревья изображаются кругами. При этом в лесу бывают сросшиеся деревья (изображения таких деревьев на карте пересекаются), также одно дерево может находиться внутри другого. Точка, в которой стоит наблюдатель, не лежит внутри или на границе ни одного из деревьев.
Входные данные
Cначала вводится целое число N - количество деревьев (1≤N≤50000). Затем идут два числа, задающих координаты наблюдателя. Затем идет N троек чисел, задающих деревья (первые два числа тройки задают координаты центра, а третье - радиус). Все координаты задаются точно и выражаются вещественными числами, по модулю не превосходящими 100000 и записанными не более чем с 2 знаками после десятичной точки.
Выходные данные
В первой строке выведите сообщение YES, если лес является дремучим, и NO - иначе. Во втором случае во вторую строку необходимо вывести координаты точки, глядя в направлении которой наблюдатель не видит деревьев (то есть луч, вдоль которого смотрит наблюдатель, не проходит внутри деревьев и не касается ни одного из деревьев). Координаты нужно вывести не менее, чем с 3 знаками после десятичной точки. Координаты не должны превышать 300000. Расстояние между выданной точкой и наблюдателем должно быть не меньше 1.
| |
![]()
|
|
Пересечение кубов
Элементарная геометрия
В пространстве с прямоугольной системой координат находятся два куба. Про них известно следующее:
- сторона каждого куба равна 2,
- центр (т.е. центр симметрии) каждого куба совпадает с началом данной системы координат,
- координаты вершин >первого куба A1A2A3A4A5A6A7A8 следующие: A1(1, 1, 1), A2(1, –1, 1), A3(–1, –1, 1), A4(–1, 1, 1), A5(1, 1, –1), A6(1, –1, –1), A7(–1, –1, –1), A8(–1, 1, –1),
- вершины второго куба B1B2B3B4B5B6B7B8 пронумерованы так, что путем поворота кубы можно совместить, и при этом совместятся соответствующие их вершины (A1 и B1, A2 и B2, … , A8 и B8)
- координаты вершин второго куба даны во входном файле.
Требуется найти объем пересечения (т.е. общей части) этих кубов.
Входные данные
Во входных данных записаны 8 троек действительных чисел – координаты вершин второго куба B1B2B3B4B5B6B7B8.
Выходные данные
В выходной файл выведите одно число – искомый объем пересечения кубов. Ответ не должен отличаться от верного более чем на 0.00001.
| |
![]()
|
|
5
Элементарная геометрия
Саша и Маша живут в разных домах одного района. Их дома находятся возле пруда в форме квадрата. Однажды глава района предложил жителям нарисовать тропинки, которые они хотели бы видеть в своём районе, чтобы в дальнейшем проложить их. Потому ребята решили рассчитать самый короткий маршрут, который может быть, чтобы пройти от одного дома к другому. На изображении ниже представлен вариант расположения пруда и двух домов ребят (зелёная точка и оранжевая). Требуется рассчитать, какое самое кратчайшее расстояние требуется им преодолеть, чтобы оказаться друг у друга в гостях.
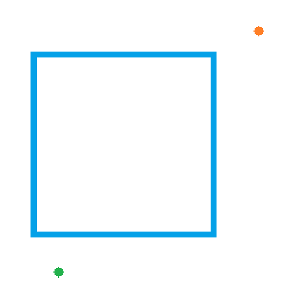
Примечание:
- дома могут находиться как по разные стороны пруда, так и поодну;
- требуется рассчитать ответ с точностью до десятых (если ответполучился целый, то выводить всегда после запятой один знак);
- передвигаться можно только по прямым, но не дугам;
- стороны пруда всегда параллельны осям OX и OY;
- точки, обозначающие дома могут лежать на границе пруда, и передвигать по границе пруда разрешено.
Формат входных данных
На первой строке подаются параметры пруда через пробел a, x1, y1 (1 <= a <= 1000; -1000 <= x1,y1 <= 1000), где x1,y1 – координаты левого верхнего угла пруда.
На второй строке подаются координаты дома Маши в виде точки xm, ym (-1000 <= xm, ym <= 1000).
На третьей строке подаются координаты дома Саши в виде точки xs, ys (-1000 <= xs, ys <= 1000).
Все числа - целые.
Формат выходных данных
Выведите на одной строке самое кратчайшее расстояние, которое можно пройти от дома Маши к дому Саши. Ответ представляет собой всегда вещественное число с одним знаком после запятой. Если ответ получился больше, то округлить до одного знака после запятой (было 4.5764, стало 4.6).
| |
![]()
|
|
65992
Элементарная геометрия
Город имеет форму круга радиуса R с центром в точке (0,0).
Сеть метро состоит из N линий метро (часть линий или все проходят через город).
Линия метро - ломаная из отрезков прямых, вершины которых имеют целочисленные координаты. Линия метро не имеет самопересечений и может быть замкнутой. Во всех точках с целочисленными координатами, через которые проходят линии метро расположены станции метро .
Для каждой точки с целочисленными координатами определим параметр вес вершины. Вес вершины — это количество станций метро, расстояние до которых не более 1 (длины клетки).
Город разбит на кварталы. Квартал — это единичная клетка с целочисленными координатами вершин, хотя бы одна из которых находящаяся строго внутри города.
Для каждого квартала определим параметр доступность. Доступность квартала равна сумме весов вершин квартала (вершина квартала может быть вне города)
Найдите значение "доступности" для каждого квартала. Для каждой полученной "доступности" определите число кварталов, имеющих эту доступность.
Входные данные
В первой строке заданы значения R, N (4<R<201, 0<N<1001)
В следующих N строках заданы описания линий метро.
Каждая линия описывается следующим образом:
первое число в строке M равно количеству вершин ломаной, далее даны координаты вершин (по два числа на вершину).
Замкнутые ломаные определяются тем, что координаты начальной и конечной вершины совпадают.
Выходные данные
В первой строке выведите число K - количество различных значений "доступности" (включая нулевую).
В следующих K строках выведите по два числа - значение "доступности" и число кварталов, имеющих такое значение "доступности"
Примеры:
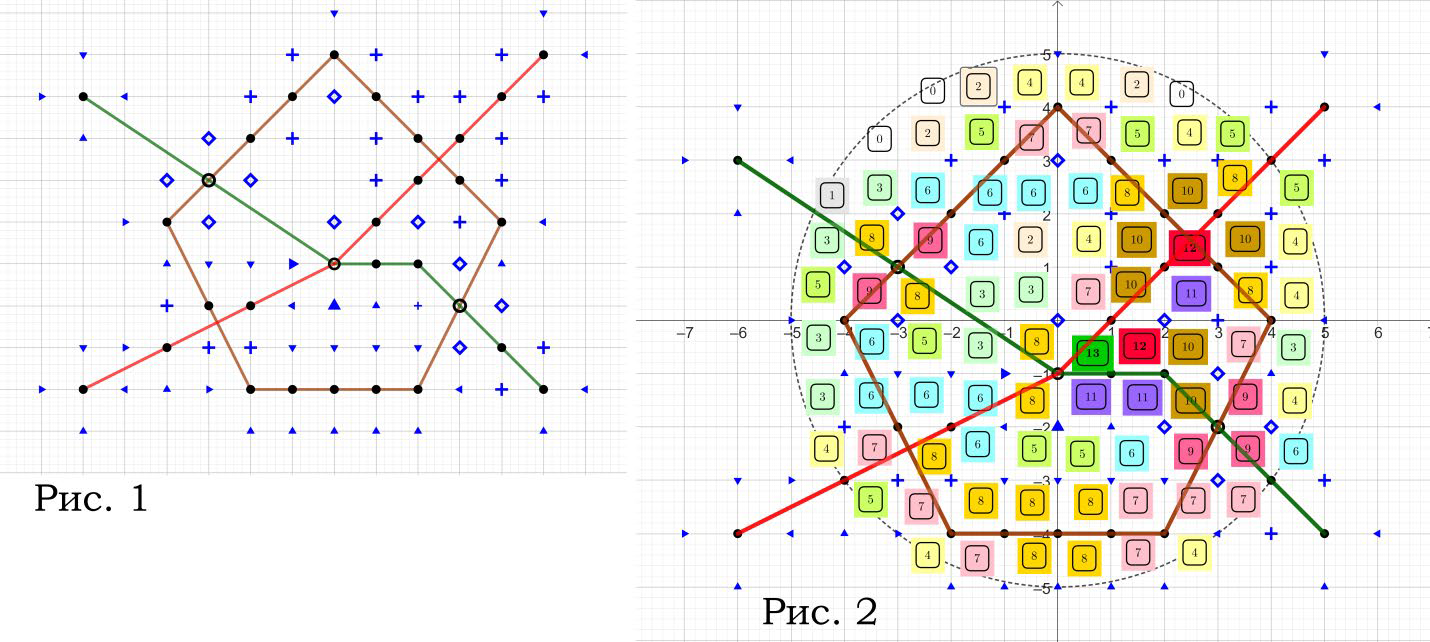
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
5 3
6 2 -4 -2 -4 -4 0 0 4 4 0 2 -4
4 -6 3 0 -1 2 -1 5 -4
3 5 4 0 -1 -6 -4 |
14
0 3
1 1
2 4
3 8
4 10
5 9
6 12
7 11
8 13
9 5
10 6
11 3
12 2
13 1 |
Город (рис. 1,2) расположен в круге радиуса 5 с центром в точке (0,0).
Сеть метро состоит из 6 линий метро (2 радиальных, 1 кольцевая):
6 2 -4 -2 -4 -4 0 0 4 4 0 2 -4 - кольцевая линия из 5 звеньев, 16 станций
4 -6 3 0 -1 2 -1 5 -4 - радиальная линия из 3 звеньев, 8 станций
3 5 4 0 -1 -6 -4 - радиальная линия из 2 звеньев, 9 станций
Есть три пересадки ( в вершинах (-3,1), (0,-1), (3,-2))
На рис.1 отмечены вершины, которые не являются станциями и
имеют не нулевой вес (треугольник - вес 1, крестик - вес 2, ромб - вес 3)
На рис.2 для всех городских кварталов указано значение параметра
доступности квартала. |
| |
![]()
|