| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Обход в глубину
Способы задания графа
У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.
Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.
Входные данные
В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.
Выходные данные
Выведите единственное число: минимальное количество копилок, которые необходимо разбить.
Примечание
Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.
Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
| |
![]()
|
1/
1
|
|
Темы:
Обход в ширину
Способы задания графа
Эпидемия гриппа не обошла стороной семиклассника Алешу. Скучая дома, Алеша решил вырезать фигурки из листа клетчатой бумаги. Лист состоял из M строк и N столбцов клеточек. Сначала Алеша нарисовал на листе границы фигур. Количество фигур было не меньше 2. Чтобы фигуры получались ровными, границы фигур Алеша рисовал строго по линиям имеющейся клеточной разметки листа (при этом некоторые границы фигур могли пройти по границам листа). Форма фигур могла быть любой, но при этом все фигуры были связными (фигура называется связной, если из любой ее клетки можно добраться до любой другой, ходя только по клеткам фигуры и перемещаясь каждый раз в одну из 4-х соседних по стороне клеток). Никакие две фигуры не имели общих точек, в том числе не касались углами клеток.
<>Затем Алеша вырезал нарисованные фигуры, делая разрезы только по их границам. При этом оставшаяся часть листа осталась связной (то есть не распалась на несколько частей).
Лист с вырезами Алеша отсканировал. Сканер в своей памяти по результатам сканирования построил таблицу, состоящую из нулей и единиц, из M строк и N столбцов (строки нумеруются сверху вниз от 1 до M, столбцы — слева направо от 1 до N). Каждый элемент таблицы соответствовал клеточке исходного листа. Единица обозначала, что соответствующая клетка листа осталась на месте, ноль — соответствующая клетка была вырезана.
На рис. 1 приведен пример клетчатого листа, а на рис. 2 — соответствующая ему таблица в памяти сканера:
Рис 1.
Исходный клеточный лист с вырезанными фигурами
Размер листа: M=6, N=12.
Количество вырезанных фигур: 3 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Рис 2.
Такая таблица строится в памяти сканера
|
После этого сканер представил полученную таблицу в специальном, описанном ниже формате и передал информацию на компьютер. Напишите программу, которая по полученной информации установит:
Пункт 1. Сколько клеток было вырезано из листа?
Пункт 2. Сколько фигур было вырезано? Описание формата представления таблицы Последовательность подряд идущих по горизонтали или вертикали единиц будем называть полосой. Полосу можно задаеть 4 числами:
- направление (0—горизонтальная, 1—вертикальная)
- (i, j) — координаты начальной клетки полосы (начальной является самая левая клетка для горизонтальной полосы, и самая верхняя — для вертикальной), i — номер строки клетки, j — номер столбца
- d — длина полосы (количество подряд стоящих единиц).
Всю таблицу разобьем на полосы, состоящие из единиц так, чтобы каждая единица принадлежала хотя бы одной полосе. При этом полосы могут пересекаться, а также накладываться. Таким образом, таблица представляется в виде описания всех полос, которое удовлетворяет трем дополнительным требованиям:
- В каждой клетке начинается не более одной полосы.
- Полосы перечислены в порядке следования их начальных клеток (клетки перечисляются по строкам сверху вниз, в строке — слева направо).
- Общее число полос не превышает 256000.
Заметим, что таблица может быть представлена в виде полос разными способами, но каждое представление позволяет однозначно восстановить таблицу.
Входные данные
Во входном файле записано сначала число P (1 или 2) — номер пункта задачи, ответ на который требуется получить. Далее записаны размеры исходного листа — числа M и N (1 ≤ M ≤ 4000,1 ≤ N ≤ 4000) . Затем записано число K (0 ≤ K ≤ 256000) — количество полос в описании полученной таблицы. Затем идет K четверок чисел, описывающих полосы (полосы перечисляются в порядке начальных клеток полос: по строкам сверху вниз, в строке — слева направо).
Выходные данные
В выходной файл выведите искомое количество (если P=1, то — количество клеток, вырезанных из листа, если P=2, то — количество фигур, вырезанных из листа).
| |
![]()
|
12/
2
|
|
Темы:
Алгоритм Флойда
Способы задания графа
На клеточном поле введена система координат так, что центр координат находится в точке пересечения линий сетки и оси направлены вдоль линий сетки.
На этом поле выложили связную фигуру, состоящую из спичек. Использовались спички двух типов:
- Спички длины 1 выкладывались по сторонам клеток.
- Спички длины выкладывались по диагоналям клеток.
Ребенок хочет сжечь фигуру. При этом он может поджечь ее в одной точке, имеющей целочисленные координаты (например, в точке A на рисунке поджигать фигуру нельзя, а в точках B и C — можно).
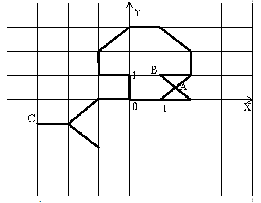
Известно, что огонь распространяется вдоль спички равномерно (но по каждой спичке — со своей скоростью). Спичка может гореть в нескольких местах (например, когда она загорается с двух концов; или когда в середине диагональной спички огонь перекидывается с одной спички на другую — огонь расползается по вновь подожженной спичке в обе стороны).
Напишите программу, которая определит, в какой точке нужно поджечь фигуру, чтобы она сгорела за минимальное время.
Входные данные
Во входном файле записано сначала число N — количество спичек (1<N<40). Затем идет N пятерок чисел вида X1, Y1, X2, Y2, T, задающих координаты концов спички и время ее сгорания при условии, что она будет подожжена с одного конца (гарантируется, что каждая спичка имеет длину 1 или , все спички образуют связную фигуру, и положение никаких двух спичек не совпадает). Все координаты — целые числа, по модулю не превышающие 200, время сгорания — натуральное число, не превышающее 107.
Выходные данные
Выведите координаты целочисленной точки, в которой нужно поджечь фигуру, чтобы она сгорела за наименьшее время, а затем время, за которое в этом случае фигура сгорит. Время должно быть выведено с точностью не менее 2-х знаков после десятичной точки. Если решений несколько, выведите любое из них.
| |
![]()
|
11/
3
|
|
Темы:
Обход в ширину
Обход в глубину
Способы задания графа
Прямоугольную таблицу, состоящую из N строк и M столбцов, раскрашивают следующим образом. Каждый столбец таблицы и каждую строку красят либо в синий, либо в желтый цвет. В итоге клетки, оказавшиеся на пересечении синего столбца и синей строки оказываются синими, желтого столбца и желтой строки — желтыми, а клетки на пересечении синего столбца и желтой строки, или, наоборот, желтого столбца и синей строки — зелеными.
Раскраска всех клеток таблицы (или просто сама таблица) называется правильной, если она может быть получена описанным выше способом.
Вам дана прямоугольная таблица, которую нужно раскрасить таким образом. Про некоторые клетки известно, какого цвета они должны быть, а остальные клетки могут в итоге быть любого цвета. Определите, сколько существует различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет.
Входные данные
Вводятся числа N и M — количество строк и столбцов таблицы (1≤N≤30, 1≤M≤30). Далее записано N строк по M чисел в каждой, задающие цвета, в которые должны быть окрашены клетки:
0 — клетка может в итоге быть любого цвета
1 — клетка должна быть синей
2 — клетка должна быть желтой
3 — клетка должна быть зеленой
Выходные данные
Выведите одно число — количество различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет. Обратите внимание, что если два или более способов раскраски столбцов и строк таблицы приводят к одинаковой раскраске самой таблицы, то это нужно считать как один вариант раскраски таблицы (см. пример 2).
| |
![]()
|
1/
1
|
|
Темы:
Обход в глубину
Способы задания графа
У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.
Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.
Входные данные
В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.
Выходные данные
Выведите единственное число: минимальное количество копилок, которые необходимо разбить.
Примечание
Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.
Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
| |
![]()
|
1/
1
|
|
Темы:
Обход в глубину
Способы задания графа
Дима обнаружил у папы на столе специальный чертежный прибор, похожий на циркуль - измеритель. Измеритель отличается от обычного циркуля тем, что в обеих его ножках находятся иголки (у обычного циркуля в одной ножке находится иголка, а в другой - грифель).
Дима взял клетчатый лист бумаги, установил между иглами измерителя некоторое расстояние, прочно зафиксировав его, и начал втыкать измеритель в лист бумаги. Каждый раз Дима втыкал в лист обе иглы измерителя, при этом он всегда делал это так, что дырочки получались в точках пересечениях линий, которыми лист разлинован на клетки. При этом в одну и ту же дырку Дима мог вставлять измеритель несколько раз.
Вечером папа нашел лист, с которым развлекался Дима, и решил выяснить, какое расстояние между иглами измерителя Дима мог установить. Все, что знает папа - координаты дырок, проделанных иглами измерителя. Помогите Папе решить поставленную задачу.
Входные данные
В первой строке вводится число n
- количество дырок (2 <= n <= 1000). Следующие n строк содержат по два целых числа - координаты дырок. Координаты не превышают 104
по абсолютной величине.
Выходные данные
В первой строке выведите k
- количество различных расстояний, которые Дима мог установить между иглами измерителя. Следующие k строк должны содержать искомые расстояния, по одному вещественному числу в строке. Расстояния должны быть выведены в возрастающем порядке. Каждое число должно быть выведено с точностью не менее, чем 10-9.
Гарантируется, что существует по крайней мере одно расстояние, которое Дима мог установить между иглами измерителя.
| |
![]()
|
2/
2
|
|
Темы:
Обход в глубину
Способы задания графа
У Пети в саду растет яблоня. Воодушевленный историей об Исааке Ньютоне, который, как известно, открыл закон всемирного тяготения после того, как ему на голову упало яблоко, Петя с целью повысить свою успеваемость по физике часто сидит под яблоней.
Однако, поскольку по физике у Пети твердая тройка, яблоки с его яблони падают следующим образом. В какой-то момент одно из яблок отрывается от ветки, на которой оно висит, и начинает падать строго вниз. Если в некоторый момент оно задевает другое яблоко, то то тоже отрывается от своей ветки и начинает падать вниз, при этом первое яблоко не меняет направление своего падения. Вообще, если любое падающее яблоко заденет другое яблоко на своем пути, то оно также начнет падать.
Таким образом, в любой момент каждое яблоко либо висит на ветке, либо падает строго вниз, причем все яблоки кроме первого, чтобы начать падать, должны сначала соприкоснуться с каким-либо другим падающим яблоком.
Выясните, какие яблоки упадут с Петиной яблони.
Входные данные
В первой строке вводится число N - количество яблок на Петиной яблоне (1 <= N <= 200). Следующие N строк содержат описания яблок. Будем считать все яблоки шарами. Каждое яблоко задается координатами своей самой верхней точки (той, где оно исходно прикреплено к дереву, длиной черенка пренебрежем) xi, yi и zi и радиусом ri ( -10000 <= xi, yi, zi <= 10000, 1 <= ri <= 10000, все числа целые). Гарантируется, что изначально никакие яблоки не пересекаются (даже не соприкасаются). Ось OZ направлена вверх.
Выходные данные
В первой строке выведите количество яблок, которые упадут с яблони, если начнет падать первое яблоко. В следующей строке выводите номера упавших яблок. Яблоки нумеруются, начиная с 1, в том порядке, в котором они заданы во входных данных.
| |
![]()
|
1/
1
|
|
Темы:
Способы задания графа
Напомним, что ориентированный граф называется транзитивным, если для любых трех различных вершин u, v и w из того, что из u в вершину v ведет ребро и из вершины v в вершину w ведет ребро, следует, что из вершины u в вершину w ведет ребро.
Проверьте, что заданный ориентированный граф является транзитивным.
Входные данные
Сначала вводится число n ( 1≤n≤100 ) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите «YES», если граф является транзитивным, и «NO» в противном случае.
| |
![]()
|
35/
11
|
|
Темы:
Способы задания графа
Напомним, что граф называется транзитивным, если всегда из того, что вершины u и v соединены ребром и вершины v и w соединены ребром следует, что вершины u и w соединены ребром.
Проверьте, что заданный неориентированный граф является транзитивным.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m (1 \leq m \leq n (n-1)/2)\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является транзитивным, и «NO» в противном случае.
| |
![]()
|
40/
9
|
|
Темы:
Способы задания графа
Ориентированный граф называется турниром, если между любой парой его различных вершин существует ровно одно ребро. Для заданного списком ребер графа проверьте, является ли он турниром.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m ( 1 \leq m \leq n (n-1))\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является турниром, и «NO» в противном случае.
| |
![]()
|
34/
14
|
|
Темы:
Способы задания графа
Ориентированный граф называется полуполным, если между любой парой его различных вершин есть хотя бы одно ребро. Для заданного списком ребер графа проверьте, является ли он полуполным.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m (1 \leq m \leq n (n-1))\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является полуполным, и «NO» в противном случае.
| |
![]()
|
42/
15
|
|
Темы:
Способы задания графа
Неориентированный граф с кратными рёбрами называется полным, если любая пара его различных вершин соединена хотя бы одним ребром. Для заданного списком ребер графа проверьте, является ли он полным.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m ( 1 \leq m \leq n (n-1)/2)\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является полным, и «NO» в противном случае.
| |
![]()
|
12/
10
|
|
Темы:
Способы задания графа
Неориентированный граф называется регулярным, если все его вершины имеют одинаковую степень. Для заданного списком ребер графа проверьте, является ли он регулярным.
Входные данные
Сначала вводятся числа n ( 1≤n≤100) – количество вершин в графе и \(m (0 \leq m \leq n (n - 1)/2)\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является регулярным, и «NO» в противном случае.
| |
![]()
|
29/
17
|
|
Темы:
Способы задания графа
Напомним, что вершина ориентированного графа называется истоком, если в нее не входит ни одно ребро и стоком, если из нее не выходит ни одного ребра.
Ориентированный граф задан матрицей смежности. Найдите все вершины графа, которые являются истоками, и все его вершины, которые являются стоками.
Входные данные
Сначала вводится число n ( 1≤n≤100) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Вначале выведите k – число истоков в графе и затем k чисел – номера вершин, которые являются истоками, в возрастающем порядке. Затем выведите информацию о стоках в том же порядке.
| |
![]()
|
22/
15
|
|
Темы:
Способы задания графа
Ориентированный граф задан списком ребер. Найдите степени всех вершин графа.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m (1 \leq m \leq n (n-1))\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите n пар чисел – для каждой вершины сначала выведите полустепень захода и затем полустепень исхода.
| |
![]()
|
32/
24
|
|
Темы:
Способы задания графа
Ориентированный граф задан матрицей смежности. Найдите полустепени захода и полустепени исхода всех вершин графа.
Входные данные
Сначала вводится число n ( 1≤n≤100) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите n пар чисел – для каждой вершины сначала выведите полустепень захода и затем полустепень исхода.
| |
![]()
|
25/
19
|
|
Темы:
Способы задания графа
Неориентированный граф задан списком ребер. Найдите степени всех вершин графа.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m (1 \leq m \leq n (n - 1) / 2)\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите n чисел – степени вершин графа.
| |
![]()
|
29/
21
|
|
Темы:
Способы задания графа
Ориентированный граф задан списком ребер. Проверьте, содержит ли он параллельные ребра.
Входные данные
Сначала вводятся числа n ( 1≤n≤1001≤𝑛≤100 ) – количество вершин в графе и m ( 1≤m≤10,0001≤𝑚≤10,000 ) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф содержит параллельные ребра, и «NO» в противном случае.
| |
![]()
|
43/
11
|
|
Темы:
Способы задания графа
Неориентированный граф задан списком ребер. Проверьте, содержит ли он параллельные ребра.
Входные данные
Сначала вводятся числа n ( 1≤n≤100) – количество вершин в графе и m ( 1≤m≤10,000 ) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф содержит параллельные ребра, и «NO» в противном случае.
| |
![]()
|
26/
20
|
|
Темы:
Способы задания графа
Ориентированный граф задан матрицей смежности. Найдите количество ребер в графе.
Входные данные
На вход программы поступает число n ( 1≤n≤100 ) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите одно число – количество ребер заданного графа.
| |
![]()
|
22/
20
|
|