| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Обход в ширину
Представьте, что вы состоите на службе во внешней разведке Межгалактического Альянса Республиканских Сил (МАРС). Одному из агентов разведки крупно не повезло, и он был захвачен на засекреченной космической базе. К счастью, внешней разведке МАРС удалось заполучить план этой базы. И вот теперь вам поручено разработать план побега.
База представляет собой прямоугольник размером NхM, со всех сторон окружённый стенами, и состоящий из квадратных отсеков единичной площади. База снабжена K выходами, до одного из которых агенту необходимо добраться. В некоторых отсеках базы находятся стены. Ваш агент может перемещаться из отсека в любой из четырех соседних с ним, если в том отсеке, куда он хочет переместиться, нет стены.
Кроме того, база снабжена системой гипертуннелей, способных перемещать агента из одного отсека базы (вход в гипертуннель) в другой (выход из гипертуннеля). Когда агент находится в отсеке, где есть вход в гипертуннель, он может (но не обязан) им воспользоваться.
Начальное положение вашего агента известно. Вам необходимо найти кратчайший путь побега (то есть путь, проходящий через минимальное количество отсеков).
Входные данные
В первой строке входного файла записаны числа N и M (2≤N≤100, 2≤M≤100), задающие размеры базы: N — количество строк в плане базы, M — количество столбцов. Во второй строке записаны начальные координаты агента XA,YA (1≤XA≤N, 1≤YA≤M). Первая координата задает номер строки, вторая — номер столбца. Строки нумеруются сверху вниз, столбцы слева направо.
Далее следуют N строк по M чисел, задающих описание стен внутри базы: 1 соответствует стенке, 0 — её отсутствию.
Далее в отдельной строке записано число H (0≤H≤1000) — количество гипертуннелей. В последующих H строках идут описания гипертуннелей. Каждый гипертуннель задается 4 числами: X1, Y1, X2, Y2 (1≤X1,X2≤N; 1≤Y1,Y2≤M) — координатами входа и выхода гипертуннеля. Никакие два гипертуннеля не имеют общего входа.
После этого в отдельной строке следует число K (1≤K≤10) — количество выходов с базы. В последующих K строках идут описания выходов с базы. Каждый выход задается двумя координатами X и Y (1≤X≤N; 1≤Y≤M).
Гарантируется, что начальные координаты агента не совпадают ни с одним из выходов и он не стоит в отсеке, занятом стеной. Никакие входы и выходы гипертуннелей, а также выходы с базы не находятся в отсеках, занятых стенами. Никакой вход в гипертуннель не совпадает с выходом с базы
Выходные данные
Если побег невозможен, выведите единственную строку с надписью "Impossible". В противном случае в первой строке выдайте число L - количество отсеков в кратчайшем пути побега. В последующих L строках последовательно выведите координаты отсеков кратчайшего пути побега. Если решений несколько, то выведите любое из них.
| |
![]()
|
1/
1
|
|
Темы:
Динамическое программирование на таблицах
Алгоритм Дейкстры
Обход в ширину
В спортзале размером NxM метров построили современный аттракцион под названием "Левый лабиринт". Для этого на полу спортзала с интервалом в 1 метр начертили линии, параллельные стенам спортзала. Таким образом, спортзал разбили на NxM клеток. Дальше некоторые из этих клеток покрасили в черный цвет.
Аттракцион заключается в том, что участника ставят в некоторой клетке спортзала и просят как можно быстрее добежать до некоторой другой клетки. При этом накладываются следующие условия:
- Участнику запрещено ходить по черным клеткам.
- Придя в какую-то клетку, участник может пойти либо прямо, либо налево, либо направо (если в соответствующем направлении клетка не покрашена в черный цвет): ходить назад, а также ходить по диагонали запрещается.
- За все время пути участнику разрешается повернуть направо (то есть пойти из текущей клетки направо относительно того, откуда он пришел в данную клетку) не более K раз.
- В начальной клетке участник может встать лицом в ту сторону, в какую ему захочется. С какой стороны участник прибежит в конечную клетку также не важно.
Известно, что на то, чтобы перебежать из клетки в соседнюю, участник тратит ровно 1 секунду. Требуется вычислить минимальное время, за которое участник сможет достичь конечной клетки.
Входные данные
Во входном файле сначала записано число K — количество разрешенных поворотов направо (целое число из диапазона от 0 до 5), затем записаны числа N и M, задающие размеры спортзала — натуральные числа, не превышающие 20. Далее записано N строк по M чисел в каждой. Число 0 обозначает непокрашенную клетку, число 1 — покрашенную, число 2 — клетку, откуда стартует участник и число 3 — клетку, куда нужно добежать (клетки, помеченные 2 и 3 являются непокрашенными). В лабиринте всегда есть ровно одна начальная клетка и ровно одна клетка, в которую нужно попасть.
Выходные данные
В выходной файл выведите минимальное время, за которое можно добраться в конечную клетку. Если попасть в конечную клетку с соблюдением всех условий нельзя, выведите –1.
| |
![]()
|
1/
1
|
|
Темы:
Обход в ширину
Обход в глубину
Карту местности условно разбили на квадраты, и посчитали среднюю высоту над уровнем моря для каждого квадрата.
Когда идет дождь, вода равномерно выпадает на все квадраты. Если один из четырех соседних с данным квадратом квадратов имеет меньшую высоту над уровнем моря, то вода с текущего квадрата стекает туда (и, если есть возможность, то дальше), если же все соседние квадраты имеют большую высоту, то вода скапливается в этом квадрате.
Разрешается в некоторых квадратах построить водостоки. Когда на каком-то квадрате строят водосток, то вся вода, которая раньше скапливалась в этом квадрате, будет утекать в водосток.
Если есть группа квадратов, имеющих одинаковую высоту и образующих связную область, то если хотя бы рядом с одним из этих квадратов есть квадрат, имеющий меньшую высоту, то вся вода утекает туда, если же такого квадрата нет, то вода стоит во всех этих квадратах. При этом достаточно построить водосток в любом из этих квадратов, и вся вода с них будет утекать в этот водосток.
Требуется определить, какое минимальное количество водостоков нужно построить, чтобы после дождя вся вода утекала в водостоки.
Входные данные
Во входном файле записаны сначала числа N и M, задающие размеры карты — натуральные числа, не превышающие 100. Далее идет N строк, по M чисел в каждой, задающих высоту квадратов карты над уровнем моря. Высота задается натуральным числом, не превышающим 10000. Считается, что квадраты, расположенные за пределами карты, имеют высоту 10001 (то есть вода никогда не утекает за пределы карты).
Выходные данные
В выходной файл выведите минимальное количество водостоков, которое необходимо построить.
| |
![]()
|
1/
1
|
|
Темы:
Обход в ширину
Способы задания графа
Эпидемия гриппа не обошла стороной семиклассника Алешу. Скучая дома, Алеша решил вырезать фигурки из листа клетчатой бумаги. Лист состоял из M строк и N столбцов клеточек. Сначала Алеша нарисовал на листе границы фигур. Количество фигур было не меньше 2. Чтобы фигуры получались ровными, границы фигур Алеша рисовал строго по линиям имеющейся клеточной разметки листа (при этом некоторые границы фигур могли пройти по границам листа). Форма фигур могла быть любой, но при этом все фигуры были связными (фигура называется связной, если из любой ее клетки можно добраться до любой другой, ходя только по клеткам фигуры и перемещаясь каждый раз в одну из 4-х соседних по стороне клеток). Никакие две фигуры не имели общих точек, в том числе не касались углами клеток.
<>Затем Алеша вырезал нарисованные фигуры, делая разрезы только по их границам. При этом оставшаяся часть листа осталась связной (то есть не распалась на несколько частей).
Лист с вырезами Алеша отсканировал. Сканер в своей памяти по результатам сканирования построил таблицу, состоящую из нулей и единиц, из M строк и N столбцов (строки нумеруются сверху вниз от 1 до M, столбцы — слева направо от 1 до N). Каждый элемент таблицы соответствовал клеточке исходного листа. Единица обозначала, что соответствующая клетка листа осталась на месте, ноль — соответствующая клетка была вырезана.
На рис. 1 приведен пример клетчатого листа, а на рис. 2 — соответствующая ему таблица в памяти сканера:
Рис 1.
Исходный клеточный лист с вырезанными фигурами
Размер листа: M=6, N=12.
Количество вырезанных фигур: 3 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Рис 2.
Такая таблица строится в памяти сканера
|
После этого сканер представил полученную таблицу в специальном, описанном ниже формате и передал информацию на компьютер. Напишите программу, которая по полученной информации установит:
Пункт 1. Сколько клеток было вырезано из листа?
Пункт 2. Сколько фигур было вырезано? Описание формата представления таблицы Последовательность подряд идущих по горизонтали или вертикали единиц будем называть полосой. Полосу можно задаеть 4 числами:
- направление (0—горизонтальная, 1—вертикальная)
- (i, j) — координаты начальной клетки полосы (начальной является самая левая клетка для горизонтальной полосы, и самая верхняя — для вертикальной), i — номер строки клетки, j — номер столбца
- d — длина полосы (количество подряд стоящих единиц).
Всю таблицу разобьем на полосы, состоящие из единиц так, чтобы каждая единица принадлежала хотя бы одной полосе. При этом полосы могут пересекаться, а также накладываться. Таким образом, таблица представляется в виде описания всех полос, которое удовлетворяет трем дополнительным требованиям:
- В каждой клетке начинается не более одной полосы.
- Полосы перечислены в порядке следования их начальных клеток (клетки перечисляются по строкам сверху вниз, в строке — слева направо).
- Общее число полос не превышает 256000.
Заметим, что таблица может быть представлена в виде полос разными способами, но каждое представление позволяет однозначно восстановить таблицу.
Входные данные
Во входном файле записано сначала число P (1 или 2) — номер пункта задачи, ответ на который требуется получить. Далее записаны размеры исходного листа — числа M и N (1 ≤ M ≤ 4000,1 ≤ N ≤ 4000) . Затем записано число K (0 ≤ K ≤ 256000) — количество полос в описании полученной таблицы. Затем идет K четверок чисел, описывающих полосы (полосы перечисляются в порядке начальных клеток полос: по строкам сверху вниз, в строке — слева направо).
Выходные данные
В выходной файл выведите искомое количество (если P=1, то — количество клеток, вырезанных из листа, если P=2, то — количество фигур, вырезанных из листа).
| |
![]()
|
12/
2
|
|
Темы:
Обход в ширину
Обход в глубину
Способы задания графа
Прямоугольную таблицу, состоящую из N строк и M столбцов, раскрашивают следующим образом. Каждый столбец таблицы и каждую строку красят либо в синий, либо в желтый цвет. В итоге клетки, оказавшиеся на пересечении синего столбца и синей строки оказываются синими, желтого столбца и желтой строки — желтыми, а клетки на пересечении синего столбца и желтой строки, или, наоборот, желтого столбца и синей строки — зелеными.
Раскраска всех клеток таблицы (или просто сама таблица) называется правильной, если она может быть получена описанным выше способом.
Вам дана прямоугольная таблица, которую нужно раскрасить таким образом. Про некоторые клетки известно, какого цвета они должны быть, а остальные клетки могут в итоге быть любого цвета. Определите, сколько существует различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет.
Входные данные
Вводятся числа N и M — количество строк и столбцов таблицы (1≤N≤30, 1≤M≤30). Далее записано N строк по M чисел в каждой, задающие цвета, в которые должны быть окрашены клетки:
0 — клетка может в итоге быть любого цвета
1 — клетка должна быть синей
2 — клетка должна быть желтой
3 — клетка должна быть зеленой
Выходные данные
Выведите одно число — количество различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет. Обратите внимание, что если два или более способов раскраски столбцов и строк таблицы приводят к одинаковой раскраске самой таблицы, то это нужно считать как один вариант раскраски таблицы (см. пример 2).
| |
![]()
|
1/
1
|
|
Темы:
Обход в ширину
На столе лежат несколько кусков ткани, не перекрывая друг друга. Эти куски могут иметь дыры, в том числе и настолько большие, что в них может поместиться целый кусок ткани. Был получен чёрно-белый образ поверхности стола, на котором области, покрытые тканью, представлены символами *, а свободные площади - точками. Один кусок ткани, таким образом, представлен 4-связной областью символов *, то есть группой *, соседствующих друг с другом горизонтально или вертикально, но не по диагонали.
.***..***
.*.*.**.*
.***.*.**
*...**.*.
На схеме три куска - один без дыр, а два - с одной дырой каждый: первый площадью 8, второй - площадью 12.
Ваша цель - найти кусок с наибольшим количеством дыр в нём. Дыра - это 4-связная область точек, полностью окружённых символами *. Если несколько кусков имеют одинаковое количество дыр, нужно выбрать кусок минимальной площади.
Входные данные
В первой строке содержатся два числа W и H, разделённые пробелами. Следующие H строк содержат по W символов каждая. Символы в этих строках - или * (ASCII 42), или точка (ASCII 46).
Ограничения: 1 <= W, H <= 100.
Выходные данные
Вывести одно целое число - площадь минимального из наиболее дырявых кусков. Если нет кусков с дырами, выходной файл должен содержать ноль.
| |
![]()
|
2/
2
|
|
Темы:
Обход в ширину
Пещера представлена кубом, разбитым на N частей по каждому измерению (то есть на N 3 кубических клеток). Каждая клетка может быть или пустой, или полностью заполненной камнем. Исходя из положения спелеолога в пещере, требуется найти, какое минимальное количество перемещений по клеткам ему требуется, чтобы выбраться на поверхность. Переходить из клетки в клетку можно, только если они обе свободны и имеют общую грань.
Ограничения: 1 <= N <= 30.
Входные данные
В первой строке содержится число N. Далее следует N блоков. Блок состоит из пустой строки и N строк по N символов: # - обозначает клетку, заполненную камнями, точка - свободную клетку. Начальное положение спелеолога обозначено заглавной буквой S. Первый блок представляет верхний уровень пещеры, достижение любой свободной его клетки означает выход на поверхность. Выход на поверхность всегда возможен.
Выходные данные
Вывести одно число - длину пути до поверхности.
| |
![]()
|
4/
3
|
|
Темы:
Обход в ширину
Элементарная геометрия
Дано N прямоугольников со сторонами, параллельными осям координат. Требуется определить, на сколько частей эти прямоугольники разбивают плоскость (внутри частей не должно быть границ прямоугольников).
Входные данные
В первой строке содержится число прямоугольников N. Далее идут N строк, содержащих по 4 числа x1, y1, x2, y2 - координаты двух противоположных углов прямоугольника.
Ограничения: 1 <= N <= 100, координаты представляют собой целые числа и по абсолютной величине не превосходят 10 000.
Выходные данные
Вывести одно число - количество частей, на которые разбивается плоскость.
| |
![]()
|
2/
2
|
|
Темы:
Обход в ширину
Дана шахматная доска, состоящая из N*N клеток, несколько из них вырезано. Провести ходом коня через невырезанные клетки путь минимальной длины из одной заданной клетки в другую.
Входные данные
В первой строке задано число N. В следующих N строках содержится по N символов. Символом # обозначена вырезанная клетка, точкой - невырезанная клетка, @ - заданные клетки (таких символов два). 2 <= N <= 50.
Выходные данные
Если путь построить невозможно, вывести "Impossible", в противном случае вывести такую же карту, как и на входе, но пометить все промежуточные положения коня символом @.
| |
![]()
|
1/
1
|
|
Темы:
Обход в ширину
В таблице из N строк и N столбцов некоторые клетки заняты шариками, другие свободны. Выбран шарик, который нужно переместить, и место, куда его нужно переместить. Выбранный шарик за один шаг перемещается в соседнюю по горизонтали или вертикали свободную клетку. Требуется выяснить, возможно ли переместить шарик из начальной клетки в заданную, и если возможно, то найти путь из наименьшего количества шагов.
Входные данные
В первой строке находится число N, в следующих N строках - по N символов. Символом точки обозначена свободная клетка, латинской заглавной O - шарик, @ - исходное положение шарика, который должен двигаться, латинской заглавной X - конечное положение шарика. 2 <= N <= 250.
Выходные данные
В первой строке выводится Y, если движение возможно, или N, если нет. Если движение возможно, далее следует N строк по N символов - как и на вводе, но X, а также все точки по пути заменяются плюсами +.
| |
![]()
|
3/
2
|
|
Темы:
Обход в ширину
Лабиринт представляет собой квадрат, состоящий из NxN сегментов. Каждый из сегментов может быть либо пустым, либо заполненным монолитной каменной стеной. Гарантируется, что левый верхний и правый нижний сегменты пусты. Лабиринт обнесён сверху, снизу, слева и справа стенами, оставляющими свободными только левый верхний и правый нижний углы. Директор лабиринта решил покрасить стены лабиринта, видимые изнутри (см. рисунок). Помогите ему рассчитать количество краски, необходимой для этого.
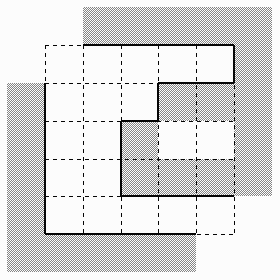
Входные данные
В первой строке находится число N, затем идут N строк по N символов: точка обозначает пустой сегмент, решётка - сегмент со стеной. 3 <= N <= 33, размер сегмента 3 x 3 м, высота стен 3 м.
Выходные данные
Вывести одно число - площадь видимой части внутренних стен лабиринта в квадратных метрах.
| |
![]()
|
2/
1
|
|
Темы:
Обход в ширину
В таблице из N строк и N столбцов некоторые клетки заняты шариками, другие свободны. Выбран шарик, который нужно переместить, и место, куда его нужно переместить. Выбранный шарик за один шаг перемещается в соседнюю по горизонтали или вертикали свободную клетку. Требуется выяснить, возможно ли переместить шарик из начальной клетки в заданную, и, если возможно, то найти путь из наименьшего количества шагов.
Входные данные
В первой строке находится число N, в следующих N строках - по N символов. Символом точки обозначена свободная клетка, латинской заглавной O - шарик, @ - исходное положение шарика, который должен двигаться, латинской заглавной X - конечное положение шарика. 2 <= N <= 40.
Выходные данные
В первой строке выводится Y, если движение возможно, или N, если нет. Если движение возможно, далее следует N строк по N символов - как и на вводе, но буква X, а также все точки по пути заменяются плюсами.
| |
![]()
|
2/
2
|
|
Темы:
Алгоритм Дейкстры
Обход в ширину
Зал супермаркета имеет форму прямоугольника размером M x N, в котором расставлены витрины размером 1 x 1. Стороны витрин параллельны стенам супермаркета, а расстояния от витрин до стен – целые числа.
В супермаркет привезли новую супервитрину размером K x 1 и выгрузили в одном из углов супермаркета. Требуется передвинуть ее в противоположный угол супермаркета. При этом ее нельзя поворачивать, а можно лишь передвигать параллельно стенам супермаркета. Напишите программу, которая по плану супермаркета поможет определить, какое наименьшее количество витрин нужно убрать, чтобы передвинуть супервитрину.

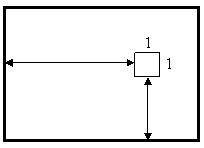
Входные данные
В первой строке вводятся три натуральных числа M, N и K (M, N ≤ 100, K ≤ M). Начальное и конечное расположение супервитрины такие, как указано на верхнем рисунке. В следующей строке записано целое неотрицательно число V – количество витрин (0 ≤ V ≤ N*M). В следующих V строках входных данных содержатся различные пары целых неотрицательных чисел, характеризующие положения витрин. Первое число (от 0 до M–1) – расстояние от левой стены супермаркета до витрины, второе (от 0 до N–1) – расстояние от нижней стены до витрины (см. нижний рисунок). Гарантируется, что там, где изначально поставили супервитрину, других витрин нет.
Выходные данные
В первой строке выведите минимальное количество витрин, которые необходимо убрать. Во второй строке выведите возможный маршрут передвижения супервитрины: одну строку из заглавных латинских букв, обозначающих следующее:
U – на 1 вверх,
D – на 1 вниз,
L – на 1 влево,
R – на 1 вправо.
Количество символов в строке не должно превышать N x M
.
Если возможных маршрутов несколько, то выведите любой из них.
| |
![]()
|
3/
1
|
|
Темы:
Обход в ширину
Для того, чтобы отойти ко сну, живущему в ЛКШ мальчику Пете необходимо почистить зубы, вымыть ноги, принять душ и т.д., одним словом, посетить умывальник. Так случилось, что в корпусе, где он проживает, смонтировано лишь два умывальника. Вообще корпус представляет собой совокупность из N холлов, некоторые из которых соединены коридорами, причем, если по коридору можно пройти в одну сторону, это вовсе не означает, что можно пройти и в другую. Это фишка архитекторов.
Так как Петя идёт умываться после отбоя, он смертельно боится попасться на глаза воспитателям ЛКШ. Однако, как выяснилось, в каждом коридоре стоит ровно по одному воспитателю, причём каждый из них считает своим долгом при встрече Пети влепить ему наряд вне очереди.
Стоит отметить ещё одну немаловажную особенность корпуса, в котором живёт Петя: архитекторы оставили потайные ходы напрямую из каждого холла в оба умывальника, но т.к. существование этих ходов приравнивается руководством к красивой легенде, в случае пользования одним из них, Петя получит 10000 нарядов вне очереди.
Петя хочет узнать, получит ли он меньше нарядов вне очереди, если пойдёт в первый умывальник, нежели если он пойдёт во второй. Обратный путь его не интересует.
Входные данные
В первой строке входного файла четыре числа: N, S, V1, V2 (1 <= N <= 1000; 1 <= S, V1, V2 <= N), где N - общее количество холлов, S - номер холла, в котором Петя находится в начальный момент времени, V1, V2 - номера холлов, в которых располагаются умывальники. В следующих N строках по N чисел - 1 или 0. Стоящий в I-ой строке на J-ом месте 0 означает отсутствие коридора из I-го холла в J-ый, а стоящая 1 - присутствие.
Выходные данные
Вывести 1, если Петя сможет получить меньше нарядов вне очереди при использовании первого умывальника, нежели при использовании второго, или 0 в противном случае.
| |
![]()
|
2/
1
|
|
Темы:
Алгоритм Флойда
Обход в ширину
Вася из задачи A по-прежнему занят поиском кладов. Более того, у него появились последователи. Один из таких последователей попросил Васю помочь в своих поисках. Так, по карте сокровищ Васю просят восстановить кратчайший путь до клада. Конфигурация лабиринта совпадает с конфигурацией, описанной в задаче A (поле \(N \times M (1 \le N, M \le 100, N \times M \le 100))\), в одной клетке которого находится клад, в K
клетках находятся входы в лабиринт).
Требуется вывести искомый путь.
Формат входных данных
Первая строка содержит 2 числа N<=100 и M<=100, задающие размеры лабиринта. Далее следует описание лабиринта: N
строк по M символов в каждой. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с сокровищем (такая клетка в лабиринте ровно одна).
В (N+2)-й строке находится число \(K (1 \le K \le N \times M)\) - количество входов в лабиринт. Далее в K строках содержатся координаты входов. Так, в i-й строке содержатся числа \(x_i\) и \(y_i\), означающие, что i-й вход расположен в \(x_i\)-й строке и в \(y_i\)-м столбце \((1 \le x_i \le N, 1\le y_i \le M)\). Гарантируется, что координаты входов попарно различны, и то, что все входы расположены в пустых клетках. Ни один из входов не находится в клетке с сокровищем.
Формат выходных данных
В первой строке вывести одно число - длину кратчайшего маршрута. В следующих строках необходимо вывести кратчайший маршрут. Каждую клетку маршрута (включая начальную и конечную) вывести на отдельной строке в формате \(x_i\) \(y_i\), где \(x_i\) - строка клетки, а \(y_i\) - столбец клетки.
Если существует несколько путей минимальной длины, выведите любой. Если до сокровища невозможно добраться, в единственной строке выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5 |
4
1 1
2 1
2 2
3 2
3 3 |
| 2 |
3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
|
-1 |
| |
![]()
|
7/
5
|
|
Темы:
Обход в ширину
В Сильвертауне есть N районов с номерами от 1 до N и M дорог с номерами от 1 до M. Используя дорогу i, вы можете добраться из района Ai в район Bi или наоборот за один час.
Сколько существует путей, по которым можно добраться из района 1 в район N как можно быстрее?
Поскольку число может быть огромным, выведите его по модулю 109+7
Формат входных данных
Первая строка содержит два целых числа N и M. Далее идет M строк, в каждой из которых записано по 2 числа: Ai и Bi.
Ограничения
2 ≤ N ≤ 2×1050 ≤ M ≤ 2×1051 ≤ Ai < Bi ≤ NПары (Ai,Bi) уникальны.Все значения во входных данных целые числа.
Формат выходных данных
Выведите ответ на задачу.
| |
![]()
|
103/
27
|
|
Темы:
Обход в ширину
Магистр Максимус отправился в опасное путешествие в горы Ордена Магов. Внутри гор великими магами прошлого созданы комнаты, в каждой из которых хранятся магические артефакты. Максимус желает пройти через все n комнат, но, как оказалось, все комнаты заперты, за исключением комнаты 0, в которую Максимус уже вошел.
В каждой комнате имеется набор уникальных заклинаний, открывающих двери других комнат. Магистр Максимус познал язык великих магов, поэтому он может легко прочитать эти заклинания и отпирать другие комнаты.
Максимус хочет посетить все комнаты и найти все магические артефакты. Однако, для этого ему необходимо найти заклинания открывающие каждую дверь.
По известному набору заклинаний, определите сможет ли Максимум получить все артефакты или нет.
Формат входных данных
В первой строке записано число n (2 <= n <= 1000), количество комнат. Далее идет n строк. В i-й строке описываются заклинания, хранящиеся в этой комнате. В каждой из этих строк первое число (m, 0 <= m <= 1000) обозначает количество уникальных заклинаний, которые открывают комнаты, далее записаны m уникальных чисел rooms[i](0 <= rooms[i][j] < n) - номера комнат, которые открывают эти заклинания (0<=i<n, 1 <= общее количество заклинаний во всех комнатах <= 10000).
Формат выходных данных
Выведите True, если Максимус может посетить все комнаты и найти все магические артефакты, или False в противном случае.
| |
![]()
|
9/
5
|
|
Темы:
Обход в ширину
Аборигены с планеты Шешинера очень любят земные ананасы. Побывав у них в гостях, Алиса решила отправить несколько штук им в подарок. На то, чтобы доставить ананасы свежими есть всего 24 часа.
Алиса хочет хочет отправить как можно большее число ананасов. Капитан Полосков решил ей помочь и с радостью согласился слетать на своем космическом корабле. Но есть один нюанс: на некоторых космических маршрутах можно дозаправить корабль, не превышающий максимально установленный вес. А заправлять корабль в пути нужно всегда, иначе он просто не долетит. Поэтому если корабль заполнить ананасами по максимуму, то, его не получится дозаправить в пути и поэтому не удастся воспользоваться самым коротким маршрутов, и придётся лететь через другие планеты. Может случиться даже так, что корабль не успеет долететь до Шешинеры вовремя, и ананасы испортятся.
Итак, сколько же ананасов можно погрузить в космический корабль, чтобы доставить груз вовремя?
Входные данные
Программа получает на вход несколько строк. В первой строке находятся числа n (1 <= n <= 500) и m - количество планет и количество космических маршрутов между планетми, соответственно. В следующих m строках записана информация о маршрутах. Каждый маршрут описывается в отдельной строке следующим образом. Сначала указаны номера планет, которые соединяются космическим маршрутом, потом время, которое тратится на перелет по этому маршруту, и, наконец, максимальный космического корабля, который можно заправить на этом маршруте. Известно, что все космические маршруты соединяют различные планеты, причем для каждой пары планет есть не более одного маршрута, непосредственно их соединяющий. Все числа разделены одним или несколькими пробелами.
Планеты нумеруются числами от 1 до n. Планеты Земля имеет номер 1, а планета Шешинера - номер n. Время перелета по маршруту задано в минутах и не превосходит 1440 (24 часа). Ограничение на массу задано в граммах и не превосходит одного миллиарда. Кроме того, известно, что один ананас весит 100 грамм, а пустой корабль - 3 тонны.
Выходные данные
Выведите одно число - максимальное количество ананасов, которое можно доставить, потратив не более 24часов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3
1 2 10 3000220
2 3 20 3000201
1 3 1 3000099
|
2
|
| |
![]()
|
2/
1
|
|
Темы:
Обход в ширину
Беззработный Дэйв от скуки соорудил в собственной гостиной лабиринт из картонных коробок. Лабиринт содержит K входов. Когда его подружка Энни вернулась, лабиринт невероятным образом разросся изнутри, а сам горе-изобретатель там заблудился и не может выбраться.
Единственное, что нашла Энни в комнате это карту лабиринта, который имеет размеры NхM клеток. На карте было обозначено место, в котором находится Дэйв (как так вышло никто не знает). Клетки лабиринта либо пустые, по которым можно пройти, либо в них находится стена и по ним проходить нельзя. У клетки может быть до 4-х смежных клеток, в которую можно пройти из текущей.
Энни пригласила вас помочь ей определить, с какого входа нужно начать свой путь, чтобы побыстрее дойти до Дейва. Если таких входов несколько, Энни пойдет со входа с наименьшим номером.
Входные данные
Программа получает на вход несколько строк. В первой строке - 2 числа N и M (1<= N, M <= 100, NxM <= 100), размеры лабиринта. Далее следует N строк по M символов в каждой - описание лабиринта. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с Дэйвом.
В (N+2)-й строке находится число K (1<=K<=NxM) -- количество входов в лабиринт. Далее в K строках содержатся координаты входов. В i-й строке содержатся числа xi и yi, означающие,что i-й вход расположен в xi-й строке и в yi-м столбце (1<=xi<=N,1<=yi<=M).
Координаты входов попарно различны, все входы расположены в пустых клетках. Ни один из входов не находится в клетке с Дэйвом.
Выходные данные
Выведите одно число - номер входа (нумерация начинается с 1). Если до Дэйва невозможно добраться, выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5
|
1
|
| 2 |
3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
|
-1
|
| |
![]()
|
39/
10
|
|
Темы:
Обход в ширину
Обход в глубину
Из прямоугольного листа клетчатой бумаги (M строк, N столбцов) удалили некоторые клетки. На сколько кусков распадётся оставшаяся часть листа? Две клетки не распадаются, если они имеют общую сторону.
Входные данные
В первой строке находятся числа M и N, в следующих M строках - по N символов. Если клетка не была вырезана, этому соответствует знак #, если вырезана - точка. 1 <= M, N <= 100.
Выходные данные
Вывести одно число.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 10
##..#####.
.#.#.#....
###..##.#.
..##.....#
.###.#####
|
5
|
| |
![]()
|
191/
48
|
|