Двумерные массивы

ID 27224. Bovine Genomics №3

ID 37042. Заполнение по диагоналям

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Входные данные: Программа получает на вход два числа n и m.
Выходные данные: Программа должна вывести полученный массив, отводя на вывод каждого числа ровно 3 символа.

Примеры

  0  1  3  6 10 14 18 22 26 30
  2  4  7 11 15 19 23 27 31 34
  5  8 12 16 20 24 28 32 35 37
  9 13 17 21 25 29 33 36 38 39

ID 37046. 12.25б

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив, отводя на вывод каждого числа ровно 3 символа.
 

Примеры

  1   5   9  13  17 
  2   6  10  14  18 
  3   7  11  15  19 
  4   8  12  16  20 

ID 37048. 12.25г

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
 

Примеры

  4   8  12  16  20 
  3   7  11  15  19 
  2   6  10  14  18 
  1   5   9  13  17

ID 37047. Заполнение матрицы - 1

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат входных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
 

Примеры

  5   4   3   2   1 
 10   9   8   7   6 
 15  14  13  12  11 
 20  19  18  17  16

ID 37049. 12.25ж

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив, отводя на вывод каждого числа ровно 3 символа.
 

Примеры

 16  17  18  19  20 
 11  12  13  14  15 
  6   7   8   9  10 
  1   2   3   4   5

ID 37050. Заполнение матрицы - 2

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.

 

Примеры

 17  13   9   5   1 
 18  14  10   6   2 
 19  15  11   7   3 
 20  16  12   8   4 

ID 37051. 12.25и

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.

ID 37052. 12.25к

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.

ID 37059. 12.25д

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных 
Программа получает на вход два числа n и m.

Формат выходных данных 
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.

Примеры

  1   2   3   4   5 
 10   9   8   7   6 
 11  12  13  14  15 
 20  19  18  17  16 

ID 37060. 12.25е

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Входные данные: Программа получает на вход два числа n и m.
Выходные данные: Программа должна вывести полученный массив, отводя на вывод каждого числа ровно 3 символа.

Примеры

  1   8   9  16  17 
  2   7  10  15  18 
  3   6  11  14  19 
  4   5  12  13  20 

ID 37073. 12.25л

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.

 

Примеры

 20  19  18  17  16 
 11  12  13  14  15 
 10   9   8   7   6 
  1   2   3   4   5 

ID 37074. 12.25м

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
 

Примеры

  5   4   3   2   1 
  6   7   8   9  10 
 15  14  13  12  11 
 16  17  18  19  20 

ID 37075. 12.25н

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
 

Примеры

 17  16   9   8   1 
 18  15  10   7   2 
 19  14  11   6   3 
 20  13  12   5   4 

ID 37076. 12.25о

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
 

Примеры

  4   5  12  13  20 
  3   6  11  14  19 
  2   7  10  15  18 
  1   8   9  16  17 

ID 37077. 12.25п

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных 
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
 

Примеры

 16  17  18  19  20 
 15  14  13  12  11 
  6   7   8   9  10 
  5   4   3   2   1 

ID 37078. 12.25р

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Формат входных данных
Программа получает на вход два числа n и m.

Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
 

Примеры

 20  13  12   5   4 
 19  14  11   6   3 
 18  15  10   7   2 
 17  16   9   8   1 

ID 7128. Таблица чемпионата - 1

Дана таблица некоторого чемпионата. Элементы главной диагонали равны 888.  Каждый элемент массива, находящийся не на главной диагонали, может быть либо однозначным либо двузначным числом, запись которых образована цифрами, обозначающими колмичество забитых (первая цифра числа) и количество пропущенных (вторая цифра числа) в данном матче. 
Например: 32 - три забитых, два пропцщенных.
0 - ноль забитых, ноль пропущенных
5 - ноль забитых, пять пропущенных

Входные данные: Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.

Выходные данные: Программа должна вывести N строк по 2 числа в каждой: общее количество забитых и общее количество пропущенных каждой командой мячей

ID 7127. Таблица чемпионата - 2

Дана таблица некоторого чемпионата. Элементы главной диагонали равны 8.  Каждый элемент массива, находящийся не на главной диагонали, может принимать следующие значения: 3 - если данная команда выиграла игру, 0 - если проиграла, 1 - если игра закончилась в ничью.

Входные данные: Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.

Выходные данные: Программа должна вывести N строк по 3 числа в каждой: количество выигрышей, количество ничьих и количество проигрышей для каждой команды. Первая строка соответствует первой команде  и т.д.

ID 7126. Минимальный на диагоналях

В квадратном массиве размером NxN, где N - нечетное число. Наименьший элемент среди стоящих на главной и побочной диагоналях поменять местами с элементом, расположенным в левом нижнем углу массива. Если наименьших элементов несколько, то поменять тот у которого номер строки и столбца меньше.

Входные данные
Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.

Выходные данные
Программа должна вывродить на экран измененный массив.
 

ID 7125. Наибольший на диагоналях

В квадратном массиве размером NxN, где N - нечетное число. Наибольший элемент среди стоящих на главной и побочной диагоналях поменять местами с элементом, стоящим на пересечении этих диагоналей. Если наибольших элементов несколько, то поменять тот у которого номер строки и столбца меньше.

Входные данные: Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные: Программа должна вывродить на экран измененный массив

ID 7124. Сумма максимума и минимума

Входные данные: Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.

Выходные данные: Программа должна вывести одно число - сумму максимального элемента главной диагонали и минимального элемента побочной диагонали

ID 7123. Сумма на диагоналях

Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.

Входные данные: программа должна вывести
1) слово YES - если сумма элементов, расположенных на главной диагонали, больше суммы элементов расположенных на побочной диагонали
2) слово NO - если условие 1 не выполняется

ID 7122. Среднее арифметическое на побочной диагонали

Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.

Выходные данные: программа должна вывести одно число - среднее арифметическое элементов побочной диагонали двумерного массива.

ID 7121. Среднее арифметическое на главной диагонали

Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.

Выходные данные: программа должна вывести одно число - среднее арифметическое элементов главной диагонали двумерного массива.

ID 7120. Сумма диагональных элементов

Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.

Выходные данные: программа должна вывести строку, в которой через пробел указаны числа являющиеся суммой тех двух элементов каждой строки, которые принадлежат главной и побочной диагоналям

ID 7119. Симметричный массив

Проверьте, является ли двумерный массив симметричным относительно главной диагонали. Главная диагональ — та, которая идёт из левого верхнего угла двумерного массива в правый нижний.

Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по N чисел, являющихся элементами массива.

Выходные данные: программа должна выводить слово yes для симметричного массива и слово no для несимметричного.

ID 6025. Обработка столбца в матрице - 2

Дан двумерный массив A[N][M] ( 2<=N<=20; M 2<=M<=20).
В первой строке вводятся через пробел количество строк - число от 0 до N-1, и количество столбцов - число от 0 до M-1.
Во второй строке вводится число s (0<=s<=20)
Далее идет ввод элементов массива построчно
Определить cумму всех элементов s-го столбца массива.

Примеры

ID 6029. Поиск требуемой строки

В метании молота состязается n спортcменов. Каждый из них сделал m бросков. (n<=20, m<=20)
Победителем считается тот спортсмен, у которого сумма результатов по всем броскам максимальна. 
Если перенумеровать спортсменов числами от 0 до n-1, а попытки каждого из них – от 0 до m-1, то на вход программа получает массив A[n][m], состоящий из неотрицательных целых чисел (0<A[n][m]<500). Программа должна определить номер строки с максимальной суммой чисел и вывести на экран эту сумму и номер строки, для которой достигается эта сумма.

Входные данные: Программа получает на вход два числа n и m, являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.

Выходные данные: Программа должна вывести  2 числа: сумму и номер строки, для которой эта сумма достигается. Если таких строк несколько, то выводится номер наименьшей из них. 

Примеры

ID 6030. Метание молота

В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Победителем соревнований объявляется тот спортсмен, у которого максимален наилучший результат по всем броскам. Таким образом, программа должна найти значение максимального элемента в данном массиве, а также его индексы.

Формат входных данных
Программа получает на вход два числа n и m (1<=n<=20;  1<=m<=20), являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел в каждой, являющихся элементами массива.

Формат выходных данных
Программа должна вывести значение максимального элемента, затем индекс строки и индекс столбца, в котором он встречается. Если в массиве несколько максимальных элементов, то нужно вывести минимальный индекс строки, в которой встречается такой элемент, а если в этой строке таких элементов несколько, то нужно вывести минимальный индекс столбца. 

ID 37169. Игра "Жизнь". Простой вариант

В некоторых клетках квадрата \( N\ х\ N\) живут микроорганизмы (не более одного в одной клетке). Каждую секунду происходит следующее:
– все микроорганизмы, у которых менее 2-х соседей, умирают от скуки (соседями называются микроорганизмы, живущие в клетках, имеющих общую сторону или вершину);
– все микроорганизмы, у которых более 3-х соседей, умирают от перенаселенности;
– на всех пустых клетках, у которых ровно в трех соседних клетках жили микроорганизмы, появляются новые микроорганизмы.
Все изменения происходят одновременно, то есть для каждой клетки сначала выясняется ее судьба, а затем происходят изменения сразу во всех клетках.
Требуется по данной конфигурации определить, во что она превратится через \(T\) секунд.

ID 6026. Обработка строки в матрице - 2

Дан двумерный массив A[N][M] ( 2<=N<=20; M 2<=M<=20).
В первой строке вводятся через пробел количество строк - число от 0 до N-1, и количество столбцов - число от 0 до M-1.
Во второй строке вводится число  k
Далее идет ввод элементов массива построчно
Определить среднее арифметическое элементов k-ой строки массива.

Примеры

ID 6027. Обработка строки в матрице - 1

Дан двумерный массив A[N][M] ( 2<=N<=20; M 2<=M<=20).
В первой строке вводятся через пробел количество строк - число от 0 до N-1, и количество столбцов - число от 0 до M-1.
Во второй строке вводится число k
Далее идет ввод элементов массива построчно
Определить количество элементов из последней строки кратных k.

Примеры

ID 6028. Обработка столбца в матрице - 2

Дан двумерный массив A[N][M] ( 1<=N<=20; M 1<=M<=20).
В первой строке вводятся через пробел количество строк - (строки массива нумеруются от 0 до N-1), и количество столбцов - (столбцы массива нумеруются от 0 до M-1)
Далее идет ввод элементов массива построчно
Определить количество двухзначных чисел из последнего столбца.

Примеры

ID 36994. Поиск в матрице

Напишите программу, которая определяет, сколько раз встречается в матрице элемент, равный K .
 

Формат входных данных
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M (1<=N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами. В последней строке записано целое число K.
 

Формат выходных данных
Программа должна вывести количество элементов матрицы, равных K.

ID 36995. Минимум и максимум в матрице

Напишите программу, которая находит минимальный и максимальный элементы в матрице. Если в матрице есть несколько одинаковых минимальных (максимальных) элементов, нужно найти индексы первого такого элемента в порядке обхода по строкам: слева направо, сверху вниз.
 

Формат входных данных
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M (1 <= N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами.

Формат выходных данных
В первой строке программа должна вывести индексы минимального элемента (строку и столбец), а затем – его значение. Нумерация строк и столбцов начинается с единицы. Все числа разделены пробелами. Во второй строке выводится информация о максимальном элементе в том же формате.

ID 36998. Вывод столбцов с максимумом

Напишите программу, которая находит в матрице столбцы, в которых есть элемент, равный максимальному.
 

Формат входных данных
В первой строке записаны, через пробел, размеры матрицы: количество строк N и количество столбцов M (1<= N, M <= 100). Далее идут  N строк, в каждой записано по M натуральных чисел, разделённых пробелами - элементы матрицы.
 

Формат выходных данных
Программа должна вывести все столбцы, в которых есть элемент, равный максимальному элементу матрицы. Каждый столбец выводится в одну строку, элементы разделяются пробелами. Столбцы должны следовать в том порядке, в котором они стоят в матрице.

ID 27238. Строка с минимальной суммой

Напишите программу, которая находит в матрице строку с минимальной суммой.
 

Формат входных данных
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M (1<=N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами.
 

Формат выходных данных
Программа должна вывести все элементы найденной строки с минимальной суммой, разделив их пробелами. Если строк с одинаковой минимальной суммой несколько, нужно выбрать из них строку с минимальным индексом.

ID 36996. Подсчет по сумме

Напишите программу, которая определяет, сколько в матрице есть K -значных чисел, сумма цифр каждого из которых кратна R .
 

Формат входных данных
В первой строке записаны, через пробел, размеры матрицы: количество строк N и количество столбцов M (1 <= N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами. Затем в двух разных строках вводятся числа K и R .
 

Формат выходных данных
Программа должны вывести одно число – количество K -значных чисел, сумма цифр каждого из которых кратна R .

ID 27237. Магический квадрат?

Формат входных данных
В первой строке вводится размер матрицы N (0 < N <= 100) . В следующих N строках вводятся строки матрицы, по N значений в каждой, разделённые пробелами.
 

Формат выходных данных
Программа должна вывести слово 'YES', если матрица является магическим квадратом, и слово 'NO', если не является.

ID 27235. Нестандартное заполнение - 1. Диагонали

Формат входных данных
Во входной строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M (1 <= N, M <= 100).
 

Формат выходных данных
Программа должна вывести полученную матрицу по строкам.

ID 27236. Нестандартное заполнение - 2. Змейка

Формат входных данных
Входная строка содержит числа N и M, разделённые пробелом (5 <= N, M <= 20).
 

Формат выходных данных
Программа должна вывести матрицу, заполненную заданным способом.

ID 27234. Простая задача

Дан двумерный массив N*M (0 < N, M <= 20).
Значения элементов массива вводятся с клавиатуры
Вывести в первой строке все угловые элементы массива, начиная с левого верхнего угла и далее, двигаясь по часовой стрелке.


Формат входных данных
В первой строке задается размер массива. N - количество строк, M - количество столбцов (\(0<N,M<=20\))
Далее идут N строк по M чисел в каждой строке - элементы двумерного массива (каждый элемент по модулю не больше 50)


Формат выходных данных
Вывести четыре числа, через один пробел, - все угловые элементы массива, начиная с левого верхнего угла и далее, двигаясь по часовой стрелке.

ID 37026. Квадратная матрица

Дано число n. Создайте двумерный массив размером nхn и заполните его по следующему правилу. На главной диагонали должны быть записаны числа 0. На двух диагоналях, прилегающих к главной, числа 1. На следующих двух диагоналях числа 2 и т.д.

Формат входных данных
На вход подается одно единственное число n (n<=10).

Формат выходных данных
Выведите на экран заполненную матрицу.

ID 37030. Побочная диагональ

Дано число n. Создайте массив размером nхn и заполните его по следующему правилу:

Числа на диагонали, идущей из правого верхнего в левый нижний угол, равны 1.
Числа, стоящие выше этой диагонали, равны 0.
Числа, стоящие ниже этой диагонали, равны 2.

Полученный массив выведите на экран. Числа в строке разделяйте одним пробелом.

ID 37032. Симметричный массив

Дано число n и двумерный массив размером nхn. Проверьте, является ли этот двумерный массив симметричным относительно главной диагонали. Выведите слово “YES”, если двумерный массив симметричный, и слово “NO” - в противном случае.

Формат входных данных
В первой строке задается число n - размер двумерного массива (n <= 10). Далее идут n строк по n чисел в каждой - элементы двумерного массива.

Формат выходных данных
Выведите на экран слово "YES", если массив симметричен, или "NO" - в противном случае

ID 37033. Диагональ ниже главной

Дан квадратный двумерный массив размером nхn и число k. Выведите элементы k-й по счету диагонали ниже главной диагонали (т.е. если k=1, то нужно вывести элементы первой диагонали, лежащей ниже главной, если k=2, то второй диагонали и т.д.).

Значение k может быть отрицательным, например, если k=−1, то нужно вывести значение первой диагонали, лежащей выше главной. Если k=0, то нужно вывести элементы главной диагонали.
 

Формат входных данных
Программа получает на вход число n (n <= 10), затем идут элементы массива  n строк по n символов в каждой строке, затем с новой строки, число k (все элементы и значение k по модулю не больше 100).
 

ID 37034. Обмен диагоналей

Дана квадратная матрица. Поменяйте местами элементы, стоящие на главной и побочной диагоналях, при этом каждый элемент должен остаться в том же столбце (то есть в каждом столбце нужно поменять местами элемент на главной диагонали и на побочной диагонали).

Формат входных данных
На вход подается число n  - размер квадратного массива (n <= 10). Далее идут n строк по n чисел в каждой - элементы массива.

Формат выходных данных
Выведите на экран матрицу после преобразования.

ID 37038. Квадранты

Заполните квадратную матрицу целыми числами по образцу. На главной и побочных диагоналях стоят нули, эти диагонали делят массив на четыре части. В верхней части записаны единицы, в правой записаны двойки, в нижней записаны тройки, в левой записаны четверки.

Формат входных данных
На вход подается одно число n - размер квадратного массива (n <= 100).

Формат выходных данных
Выведите на экран заполненную квадратную матрицу.

ID 37083. Замена столбца на элементы массива

Дана матрица размером NxM и массив чисел размером N. В данной матрице заменить все элементы столбца с максимальной суммой элементов на элементы заданного массива чисел. Если таких столбцов несколько, то заменить элементы в столбце с меньшим индексом.

Входные данные
В первой строке задаются числа N и M (\(0<N,M<=10\)). Далее идут N строк по M чисел в каждой. Каждое число по модулю не более 100. В последней строке идут N чисел массива.

Выходные данные 
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа. После вывода каждого числа должен следовать знак пробела.
 

Пример

 52  16  61  76 
  5   5  33  69 
 37  34  14  26 

ID 37085. Обмен строк

Дана матрица размером NxM и два числа k1 и k2. Поменяйте местами строки с индексами k1 и k2.

Входные данные
В первой строке задаются числа N и M (\(0<N,M<=10\)). Далее идут N строк по M чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идут два числа k1, k2 (\(0<k1,k2<=N\)).

Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
 

Пример

 33  76  69  59  58 
 48  93  27   9  76 
 72  50  18  79  74 
 19  65  53  90  77

ID 37087. Удаление строк

В двумерном массиве хранятся результаты (время в минутах), показанные каждым из N автогонщиков на каждом из 10-ти этапов соревнований "Формула-1" (в нулевой строке - результаты первого гонщика, в первой - второго и т.д.). После десятого этапа гонщик с порядковым номером K выбыл из соревнований. Судейской коллегией было принято решение удалить результаты данного участника из таблицы.
Измените массив соответствующим образом и выведите его на экран.

Под удалением строки в двумерном массиве будем понимать:
1) исключение этой строки из массива путем смещения всех следующих за ней строк на одну вверх;
2) присваивание всем элементам последней строки значения 0 (или уменьшение количества строк на 1).

Входные данные
В первой строке задаётся число N (\(0<N<=30\)). Далее идут N строк по 10 чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идет число K (\(1<=K<=N\)).

Выходные данные 
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
 

Пример

 38  43  82  95  20 100  99  83  77  42 
 94  92  74  30  93  75  99   6  79  68 
 62  97  14  40  70  31   3  84  33  74 
 99  30  91  15  41  54  87  31  71  74 

ID 37087. Удаление строк

В двумерном массиве хранятся результаты (время в минутах), показанные каждым из N автогонщиков на каждом из 10-ти этапов соревнований "Формула-1" (в нулевой строке - результаты первого гонщика, в первой - второго и т.д.). После десятого этапа гонщик с порядковым номером K выбыл из соревнований. Судейской коллегией было принято решение удалить результаты данного участника из таблицы.
Измените массив соответствующим образом и выведите его на экран.

Под удалением строки в двумерном массиве будем понимать:
1) исключение этой строки из массива путем смещения всех следующих за ней строк на одну вверх;
2) присваивание всем элементам последней строки значения 0 (или уменьшение количества строк на 1).

Входные данные
В первой строке задаётся число N (\(0<N<=30\)). Далее идут N строк по 10 чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идет число K (\(1<=K<=N\)).

Выходные данные 
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
 

Пример

 38  43  82  95  20 100  99  83  77  42 
 94  92  74  30  93  75  99   6  79  68 
 62  97  14  40  70  31   3  84  33  74 
 99  30  91  15  41  54  87  31  71  74 

ID 37088. Удаление столбцов

В двумерном массиве хранятся результаты (время в минутах), показанные каждым из \(N\) велогонщиков на каждом из 12-ти этапов соревнований (в нулевом столбце - результаты первого этапа, в первом - второго и т.д.) Судейской коллегией результаты K-го этапа были признаны недействительными и были удалены из таблицы.
Измените массив соответствующим образом и выведите его на экран.

Под удалением столбца в двумерном массиве будем понимать:
1) исключение этого столбца из массива путем смещения всех следующих за ним столбцов на один влево;
2) присваивание всем элементам последнего столбца значения 0 (или уменьшение количества столбцов на 1).

Входные данные
В первой строке задаётся число N (0<N<=30). Далее идут N строк по 12 чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идет число K (1<=K<=12).

Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
 

Пример

 65   2  22  41  18  80  15  35  20  21  27 
  7  28  35  15  27  87  95  73  45  26  28 
  1  99  11  11  13  80  78   3  53  76  73 
 87  37  11  72  33  59  79  61  53  80  67 

ID 37084. Циклический сдвиг построчно

Каждую строку заданной прямоугольной матрицы NxM сдвинуть циклически вправо на количество позиций, равных номеру строки (нумерация строк и столбцов с 0). Вывести на экран преобразованную матрицу.

Входные данные
В первой строке находятся два числа N и M (\(0 < N,M <= 10\)). Далее идут N строк по M чисел в каждой - элементы матрицы (каждый элемент не более 100 по модулю).

Выходные данные
Вывести измененную матрицу. Каждый элемент матрицы выводится в 3 знакоместах и с одним пробелом после него.
Оформите сдвиг вправо на K позиций в виде подпрограммы.
 

Пример

 47  63  22  75 
 70  69  69  12 
 13  31  70  90 

ID 37086. Обмен столбцов

Дана матрица размером NxM и два числа k1 и k2. Выполните циклическую перестановку столбцов влево, находящихся между столбцами k1 и k2 (включая столбцы k1 и k2, т.е. столбец k1 должен оказаться на месте столбца k2, столбец k2 не месте столбца k2-1 и т.д.).

Входные данные
В первой строке задаются числа N и M (\(0<N,M<=10\)). Далее идут N строк по M чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идут два числа k1, k2 (\(0<= k1<=k2< M\)).

Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
 

Пример

 32  94  56  12 
 72  51  15  60 
  4  97  43  38 

ID 37089. Вставка столбцов

В двумерный массив записаны годовые оценки по десяти предметам каждого из N учеников класса (в нулевом столбце - оценки по первому предмету, в первом - по второму и т.д.), но по ошибке забыли вписать в массив оценки еще по одному предмету, который должен находиться в столбце K. Измените массив так, чтобы он был заполнен надлежащим образом. 

Под добавлением столбца в двумерный массив будем понимать:
1) увеличение числа столбцов массива на 1;
2) смещение всех столбов после K-го на один вправо;
3) присваивание заданных значений элементам K-го столбца.

Входные данные
В первой строке задаётся число N (0<N<=30). Далее идут N строк по 10 чисел в каждой. Каждое число в диапазоне от 2 до 5. В следующей строке идет число K (1<=K<=10). Далее, в последней строке (без пропуска строк) идет N чисел, оценки соответствующего ученика по новому предмету.

Выходные данные
Выведите на экран преобразованную матрицу, отделяя каждый элемент одним пробелом.
 

Пример

5 5 3 4 2 4 1 3 3 4 4 
5 3 3 1 2 3 4 3 2 4 3 
3 2 4 5 4 2 1 4 2 2 4 
5 1 3 5 1 1 1 5 3 4 1 
3 3 4 2 1 5 3 3 5 2 1

ID 37082. Изменение строки с максимумом

В матрице размером NхM заменить на значение -1 все элементы тех строк, в которых находится максимальный элемент.

Формат входных данных
В первой строке находятся два числа N и M (\(0 < N,M <= 10\)). Далее идут N строк по M неотрицательных чисел в каждой - элементы матрицы (каждый элемент меньше 100).

Формат выходных данных
Вывести измененную матрицу. На каждый элемент в выводе отводить ровно 3 символа (знакоместа). После вывода каждого числа должен следовать знак пробела.

Пример

 15  68  54  79  89 
 91  57  21  70  24 
 14  22   5  26  76 
 -1  -1  -1  -1  -1 
 50  62  50  58   1 

ID 38140. Комфорт для коров

Пастбище Фермера Джона может быть представлено как огромная 2D-решётка ячеек (огромная шахматная доска). Изначально пастбище пустое.
Фермер Джон добавит N (1≤N≤10⁵) коров на пастбище одну за одной. i-ая корова занимает ячейку (x_i,y_i), которая отличается от ячеек, занятых всеми другими коровами (0≤x_i,y_i≤1000).

Говорят, что корове "комфортабельно", если по горизонтали и вертикали она имеет ровно три других коровы. Фермер Джон хочет посчитать, скольким коровам комфортабельно на его пастбище. Для каждого i в интервале 1…N, выведите общее количество коров, которым комфортабельно после того, как i-ая корова добавлена на пастбище.

Входные данные: 
Первая строка содержит одно целое число N. Каждая из последующих N строк содержит два разделённых пробелом целых числа, указывающих (x,y) - координаты ячейки коровы. Гарантируется, что все ячейки различны.
Выходные данные: 
i-ая строка вывода должна содержать общее количество коров, которым комфортабельно после добавления i-ой коровы на пастбище.
 

Примеры

ID 38194. Шахматная доска

Из шахматной доски по границам клеток выпилили связную (не распадающуюся на части) фигуру без дыр. Требуется определить ее периметр.

Входные данные
Сначала вводится число N (1 ≤ N ≤ 64) – количество выпиленных клеток. В следующих N строках вводятся координаты выпиленных клеток, разделенные пробелом (номер строки и столбца – числа от 1 до 8). Каждая выпиленная клетка указывается один раз.

Выходные данные
Выведите одно число – периметр выпиленной фигуры (сторона клетки равна единице).

Примеры

ID 38202. Шахматное домино

Комплект шахматного домино состоит из 32 костяшек 2x1, каждая из квадратов которой окрашен в черный или белый цвет (часть костяшек состоит из двух белых квадратов, часть – из двух черных, а часть из одного белого и одного черного). Комплект такого домино выложен на шахматную доску. Разрешается поворачивать костяшки домино на 180 градусов (менять местами их квадраты), оставляя каждую костяшку на своем месте. Требуется выяснить, можно ли так повернуть часть костей домино, чтобы в каждом горизонтальном ряду были квадраты только одного цвета.


Входные данные
Вводится 8 строк по 8 чисел. Каждое число соответствует номеру доминошки, которая покрывает данную клетку. Число положительное, если квадрат доминошки белый и отрицательное – если черный.


Выходные данные
Требуется вывести одно слово – YES или NO (заглавными буквами).

Примеры

ID 38222. Магический квадрат

Магическим квадратом называют таблицу, в которой записаны числа 123…  по одному разу, так что сумма чисел в каждой строке и в каждом столбце равные. Мы расскажем вам об одном из методов построения магических квадратов (его называют сиамским). Он годится только для построения квадратов с нечетной стороной (3355…) .

Поставим число 1 в верхнюю клетку центрального столбца. Далее будем двигаться по диагонали вправо-вверх, расставляя в клетки последовательно числа 234… . Если мы вышли за пределы таблицы вверх, то нужно перейти к нижней клетке того же столбца и продолжить с нее. Если мы вышли за правую границу, нужно перейти к левой клетке той строки, куда мы должны были попасть. Если же мы одновременно вышли и вверх, и вправо, то нужно перейти в левую нижнюю клетку квадрата.

Если в следующей клетке на нашем пути уже стоит число, то вместо хода “вправо-вверх” нужно сделать ход “вниз” (опять же, если мы при этом выйдем за границы квадрата, нужно перейти к верхней клетке того же столбца). Примеры для квадратов 33 и 55 показаны на рисунках.



Входные данные
На вход подается одно натуральное нечетное число N, не превосходящее 30 – размер квадрата.

Выходные данные
Выведите числа, записанные в квадрате. Выравнивать числа по столбцам не обязательно. Обратите внимание: требуется вывести именно магический квадрат, полученный применением указанного метода.

Примеры

ID 38252. Муравьиная ферма

На прошлый день рождения Олегу подарили муравьиную ферму и трех больших муравьев для нее. Ферма представляет собой поле размером a × b клеток. Клетка с координатой (1, 1) находится в левом верхнем углу. Вскоре он заметил, что передвигаясь по своему вольеру, муравьи оставляют на белом песке следы разных цветов. На протяжении нескольких месяцев Олег наблюдал за своей фермой и, наконец, смог строго описать происходящее в вольере.

Клетки бывают четырех цветов:

• белая (это значит, что клетка не покрашена ни одним из муравьев, обозначается цифрой 0)
• красная (это — цвет следа первого муравья, обозначается цифрой 1)
• желтая (это — цвет следа второго муравья, обозначается цифрой 2)
• зеленая (это — цвет следа третьего муравья, обозначается цифрой 3)

• красит ее в свой цвет
• поворачивается на 90°  вправо и делает шаг вперед

• стирает с нее след (то есть красит клетку в белый цвет)
• поворачивается на 90º влево и делает шаг вперед

ID 38259. "Сапер" с подсказками

На весенних каникулах Оля долго обдумывала свое поведение и решила в четвертой четверти заниматься учебой побольше. Но уже первый урок биологии в новой четверти уничтожил все Олины благие намерения. Оле скучно, просто невыносимо скучно. От нечего делать она начала играть на своем телефоне в известную игру «Сапер».

На всякий случай напомним, в чем заключается эта игра. Игра происходит на поле размером N × M клеток, некоторые из которых «заминированы». Целью игры является открытие всех клеток, не содержащих мины.

Игрок открывает клетки, стараясь не открыть клетку с миной. Открыв клетку с миной, он проигрывает. Если под открытой ячейкой мины нет, то в ней появляется число, показывающее, сколько ячеек, соседствующих с только что открытой, «заминировано». Клетки считаются соседствующими, если у них есть общая сторона или общая вершина. Клетки, которые игрок считает «заминированными», можно пометить флажком, чтобы случайно не открыть их.

Оля играет в версию «Сапера» со встроенными подсказками. Одна из подсказок, «Показать ошибки», работает следующим образом. Если по соседству с клеткой, в которой записано некоторое число, находится больше флажков, чем может соседствовать с этой клеткой (то есть больше флажков, чем число, записанное в клетке), все флажки вокруг этой клетки подсвечиваются желтым цветом. Другие ошибки эта подсказка находить не умеет, иначе играть было бы совсем не интересно.

Ваша задача — по текущему состоянию игрового поля определить, какие флажки окажутся подсвечены желтым после запуска подсказки.

Входные данные
В первой строке содержатся два числа N и M, разделенные пробелами — высота и ширина таблицы соответственно (1 ≤ N ≤ 15, 1 ≤ M ≤ 15). В следующих N строчках содержится по M символов в каждой. Эти строчки задают игровое поле. Используются следующие обозначения:

F — флажок;

* — закрытая клетка;

Цифра от 0 до 8 — открытая клетка. Сама цифра обозначает, сколько суммарно мин находится в клетках, соседствующих с данной.

Выходные данные
В первой строке выведите количество флажков, которые окажутся подсвечены желтым, а в следующих N строчках выведите для каждого такого флажка его координаты — номер строки, а затем номер столбца, в котором стоит флажок. Флажки можно выводить в любом порядке.

Если подсвеченных флажков не будет, выведите единственное число 0
 

Примеры

ID 38336. Остров

На клетчатой бумаге нарисована карта острова (клетки острова закрашены). При этом остров является клетчато-выпуклой фигурой, то есть каждая горизонтальная или вертикальная линия на карте либо не пересекает остров, либо пересекает его по отрезку (линия пересечения не содержит разрывов). Также остров является связной фигурой, то есть любые две клетки острова соединены путём, каждые две соседние клетки которого имеют общую сторону.

Клетка считается соседней с островом, если она не принадлежит острову, но имеет общую сторону или угол с одной из клеток острова. Например, на следующей карте клетки острова закрашены, а соседние с островом клетки отмечены звёздочками.


Самолёт должен облететь вокруг острова по соседним с ним клеткам, не вторгаясь на территорию острова. Программа должна составить маршрут полёта самолёта. Самолёт начинает облёт острова в одной из соседних клеток с островом и должен побывать во всех клетках, соседних с островом, ровно один раз. При этом самолёт может перемещаться из одной клетки в другую клетку, только если эти клетки имеют общую сторону.

Выходные данные
Программа получает на вход два числа N и M, записанные в отдельных строках, — количество строк и столбцов карты острова (3 ≤ N ≤ 100, 3 ≤ M ≤ 100). Далее записана карта острова — N строк, каждая содержащая M символов. Каждый символ карты может быть либо символом «.», что означает клетку, не принадлежащую острову, либо символом «#», что означает клетку острова. При этом остров не касается края карты.

Введём на карте систему координат. Первая координата является номером строки, строки нумеруются сверху вниз числами от 1 до N. Вторая координата — номер столбца, столбцы нумеруются слева направо числами от 1 до M.

Входные данные
Программа должна вывести координаты клеток карты в порядке их облёта самолётом. Каждая строка вывода должна содержать два числа x и y — координаты самолёта, записанные через пробел (1 ≤ x ≤ N, 1 ≤ y ≤ M). Самолёт должен побывать в каждой соседней с островом клетке ровно один раз. Каждые две клетки, идущие подряд в выводе, должны иметь общую сторону. Можно вывести любой возможный маршрут облёта острова.

Примеры

6
7
.......
.......
.......
.###...
.###...
.......

ID 38360. Луч света в темном царстве

Темное царство представляет собой лабиринт NxM, некоторые клетки которого окружены зеркальными стенами, а остальные — пустые. Весь лабиринт также окружен зеркальной стеной. В одной из пустых клеток лабиринта поставили светофор, который испускает лучи в 4 направлениях: под 45 градусов относительно стен лабиринта. Требуется изобразить траекторию этих лучей.

Когда луч приходит в угол, через который проходят зеркальные стены, дальше он идет так, как показано на рисунках (серым цветом показаны клетки, которые окружены зеркальными стенами). Аналогичным образом луч ведет себя, когда приходит на границу лабиринта.


Входные данные
В первой строке входного файла записаны два натуральных числа N и M — число строк и столбцов в лабиринте (каждое из чисел не меньше 1 и не больше 100). В следующих N строках записано ровно по M символов в каждой — карта лабиринта. Символ * (звездочка) обозначает клетку, окруженную зеркальными стенками, . (точка) — пустую клетку, символ X (заглавная латинская буква X) — клетку, в которой расположен светофор (такая клетка ровно одна).

Выходные данные
В выходной файл выведите N строк по M символов в каждой — изображение лабиринта с траекториями лучей. Здесь, как и раньше, * (звездочка) должна обозначать клетки, окруженные зеркальными стенами, . (точка) — пустые клетки, через которые лучи света не проходят, / (слеш) — клетки, через которые луч света проходит из левого нижнего угла в правый верхний (или обратно — из правого верхнего в левый нижний), \ (обратный слеш) — клетки, через которые луч проходит из левого верхнего угла в правый нижний (или обратно), а символ X (заглавная латинская буква X) — клетки, через которые лучи проходят по обеим диагоналям.

Примеры

3 5
X....
.....
.....

XXXXX
XXXXX
XXXXX

3 3
...
..X
...

/X\
X.X
\X/

ID 38377. Флаг

Иннокентий работает на блошином рынке, продавая посетителям всякий хлам необычные вещи. Недавно он нашёл у себя на складе старое прямоугольное покрывало. Как оказалось, это покрывало имеет сетчатую форму, то есть покрывало состоит из nm цветных лоскутков, разбитых на n строк и m столбцов.

Цветные лоскутки привлекли внимание Иннокентия, и он сразу же придумал, как можно заработать на своей находке. Если вырезать из покрывала подпрямоугольник, состоящий из трёх цветных полос, то потом этот подпрямоугольник можно будет продать как флаг какой-нибудь страны. В частности, Иннокентий считает, что подпрямоугольник будет достаточно похож на флаг какой-нибудь страны, если он будет состоять из трёх одноцветных полос одинаковой высоты, находящихся друг под другом. Разумеется, цвет верхней полосы не должен совпадать с цветом средней полосы, а цвет средней не должен совпадать с цветом нижней.

Иннокентий пока не знает из какой части покрывала будет вырезать флаг, однако он точно решил, что будет вырезать флаг только по линиям сетки, при этом покрывало ни в коем случае нельзя поворачивать. Помогите Иннокентию и посчитайте количество различных подпрямоугольников, которые можно вырезать из покрывала и продать как флаг. Подпрямоугольники, образующие одинаковые флаги, однако расположенные в разных местах покрывала, считаются различными.



Входные данные
Первая строка содержит два целых числа n и m (1 ≤ n, m ≤ 1000 ) — количество строк и столбцов в покрывале.

Каждая из следующих n строк описывает очередную строку покрывала и состоит из m строчных латинских букв от « a » до « z », где одинаковым цветам соответствуют одинаковые буквы, а разным цветам — разные буквы.

Выходные данные
В единственной строке выведите одно целое число — количество подпрямоугольников, являющихся флагами.

Примечание

Примеры

ID 38471. Гипер-минимум

Имеется 4-мерный массив X, каждый индекс которого может принимать значения от 1 до N. Вы должны построить новый 4-мерный массив Y , элементы которого должны принимать следующие значения: Y [i₁, i₂, i₃, i₄] = min(X[j₁, j₂, j₃, j₄]), где 1 ≤ i_k ≤ N − M + 1, i_k ≤ j_k ≤ i_k + M − 1, а M -  заданное число.

Входные данные
В первой строке входного файла задаются N и M (1 ≤ M ≤ N). Остальные строки файла содержат элементы массива X. Количество элементов не будет превышать 1500000 и сами они будут целыми числами, не превышающими по абсолютному значению 10⁹. Они расположены в таком порядке, что считать их можно с помощью псевдокода:

for i = 1 to N:
for j = 1 to N:
for k = 1 to N:
for l = 1 to N:
read X[i, j, k, l]

Выходные данные
Выведите искомый массив Y в том же формате, в котором был дан массив X.
 

Примеры

ID 38434. Игра с фишками

Вы являетесь одним из разработчиков новой компьютерной игры. Игра происходит на прямоугольной доске, состоящей из W×H клеток. Каждая клетка может либо содержать, либо не содержать фишку (см. рисунок).
Важной частью игры является проверка того, соединены ли две фишки путем, удовлетворяющим следующим свойствам:
1.    Путь должен состоять из отрезков вертикальных и горизонтальных прямых.
2.    Путь не должен пересекать других фишек.
При этом часть пути может оказаться вне доски. Например:

Примеры

5 4
XXXXX
X...X
XXX.X
.XXX.
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0

4 4
XXXX
.X..
..X.
X...
1 1 3 1
0 0 0 0

ID 38796. Состязания

В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Победитель определяется по лучшему результату. Определите количество участников состязаний, которые разделили первое место, то есть определите количество строк в массиве, которые содержат значение, равное наибольшему.

Входные данные
Программа получает на вход два числа n и m, являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.

Выходные данные
Программа должна вывести  одно число - количество победителей соревнования.

 Примеры

ID 38836. Таблица умножения

Даны два числа n и m. Создайте двумерный массив A[n][m], заполните его таблицей умножения A[i][j]=i*j и выведите на экран. При этом нельзя использовать вложенные циклы, все заполнение массива должно производиться одним циклом.
Входные данные
Программа получает на вход два числа n и m – количество строк и столбцов, соответственно.

Выходные данные
Программа должна вывести  полученный массив. Числа разделяйте одним пробелом.
 

Примеры

ID 38842. Треугольник Паскаля

Даны два числа n и m. Создайте двумерный массив размерностью nхm и заполните его по следующему правилу:
- числа, стоящие в строке 0 или в столбце 0 равны 1 (A[0][j]=1, A[i][0]=1);
- значения остальных элементов массива должны быть равны сумме элементов, стоящих на один слобец левее и на одну строку выше от этого элемента. 

Входные данные
Программа получает на вход два числа n и m.

Выходные данные
Выведите на экран получившийся массив.
 

Примеры

3 3

1 1 1
1 2 3
1 3 6

ID 38875. Спираль

Робот перемещается по клетчатой плоскости и рисует спираль. Исходно он находится в клетке (0, 0) и направлен в сторону увеличения первой координаты.
Далее он действует по следующему алгоритму: совершает d перемещений вперед, затем поворачивает налево и снова делает d перемещений вперед. После этого он поворачивает налево и умножает значение d на k. Затем робот повторяет описанный процесс. Робот останавливается, сделав суммарно ровно n перемещений.
Требуется вывести картинку, на которой отмечены клетки, на которых побывал робот.

Входные данные
На вход подаются целые числа n, d и k (1 ≤ n ≤ 1000, 1 ≤ d ≤ 100, 2 ≤ k ≤ 5).

Выходные данные
Пусть минимальный прямоугольник из клеток, содержащий все посещенные роботом клетки, имеет высоту h и ширину w. На первой строке выведите числа h и w, разделенные пробелом. Следующие h строк должны содержать по w символов, выведите «*» для клетки, посещенной роботом и «.» для не посещенной.

Примеры

5 5
*****
*...*
*.***
*....
**...

ID 33220. Матрицы. Введение

Объявите в программе три матрицы с начальными значениями
        - матрицу A размером 5 на 6 элементов, в которой первый элемент каждой строки равен номеру строки, остальные элементы строки - нули
        - матрицу B  размером  10 на 10, заполненную нулями
        - матрицу С размером 2 на 2, где каждый элемент равен сумме номера строки и номера столбца

ID 27171. Златопольский 12.5

Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M(1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают  50.
Далее идет число k (1<=k<=N) 

Формат выходных данных
Вывести на экран k-ю строку (считая, что нумерация элементов массива начинается с 1, т.е. для первой строки k=1).
Все элементы выводить в одну строку через 1 пробел между элементами

ID 27170. Златопольский 12.3

Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают  50.
Далее, через пробел, идут два числа k и h (1<=k<=N, 1<=h<=M) 

Формат выходных данных
Вывести на экран элемент, расположенный на позиции h в строке k (считая, что нумерация элементов массива начинается с 1, т.е. для левого верхнего элемента массива считается, что k=1 и h=1).

ID 27169. Златопольский 12.2б

Формат входных данных
В первой строке вводятся через пробел количество строк N(1<=N<=20) и количество столбцов M (1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают  50.

Формат выходных данных
Вывести на экран элемент, расположенный в левом верхнем углу.

ID 27168. Златопольский 12.2а

Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (1<=N<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают  50.

Формат выходных данных
Вывести на экран элемент, расположенный в правом нижнем углу.

ID 27167. Златопольский 12.1б

Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (1<=N<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают  50.

Формат выходных данных
Вывести на экран элемент, расположенный в левом нижнем углу.

ID 27166. Златопольский 12.1а

Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (M 1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают  50.

Формат выходных данных
Вывести на экран элемент, расположенный в правом верхнем углу.

ID 7118. 7118

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

ID 7117. 7117

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

ID 7116. 7116

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

1 0 0 0 0 
1 1 0 0 0 
1 1 1 0 0 
1 1 0 0 0 
1 0 0 0 0 

Примеры

1 0 0 0 0 
1 1 0 0 0 
1 1 1 0 0 
1 1 0 0 0 
1 0 0 0 0 

ID 23073. 23073

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

ID 23072. 23072

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

ID 7115. 7115

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

ID 7114. 7114

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

ID 7113. 7113

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

ID 7112. 7112

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
- числа на диагонали, идущей из левого нижнего в правый верхний угол, равны 1; 
- числа, стоящие ниже этой диагонали, равны 0;
- числа, стоящие выше этой диагонали, равны 2.

Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных

ID 7111. Квадратная матрица

Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:

ID 37092. 12.41

В двумерном массиве хранится информация о зарплате N человек за каждый из 12 месяцев года (в строках находится информация о людях, в столбцах о месяцах). Составить программу для расчета общей суммы, выплаченной работникам за K-й месяц года (месяцы нумеруются с 1).

Входные данные 
В первой строке задается число N (0< N <= 25). Далее идут N строк по 12 чисел в каждой (каждое число - натуральное число, не более 150). В последней строке задается число K (1 <= K <= N).

Выходные данные 
Выведите на экран отве на задачу.

Примеры

ID 37091. 12.39

В зрительном зале N рядов, в каждом из которых M мест (кресел). Информация о проданных билетах хранится в двумерном массиве, номера строк соответсвуют номерам рядов, а номера столбцов - номерам мест. Если билет продан на то или иное место, то соответствующий элемент массива имеет значение 1, в противном случае - 0. Составить программу, определяющую число проданных билетов на места в K-м ряду.

Входные данные: в первой строке задаются два числа N (0<N<=15) и M (0<M<=25)
Далее идут N строк по M чисел в каждой (каждое число равно  0 или 1)
В последней строке идет число K (1<=K<=N)
Выходные данные: выведите ответ на задачу

Примеры

ID 37090. Обработка строки в матрице - 3

В двумерном массиве хранится информация о баллах, полученных спортсменами-пятиборцами в каждом из пяти видов спорта (в нулевой строке - информация о баллах первого спортсмена, в первой - второго и т.д.). Общее число спорстменов \(N\). Определите общую сумму баллов, набранных \(K\)-м спортсменом.

Входные данные: в первой строке задается число \(N\) (\(0<N<=20\)). 
Далее идут N строк по 5 чисел в каждой - баллы, полученные спортсменами (каждое число - натуральное, не более 50)
В последней строке задается число \(K\)
Выходные данные: выведите на экран ответ на задачу

Примеры

ID 37097. 37097

В зрительном зале N рядов, в каждом из которых по M мест (кресел). Информация о проданных билетах хранится в двумерном массиве, номера строк которого соответствуют номерам рядов, а номера столбцов - номерам мест (места нумеруются с 1). Если билет на то или иное место продан, то в массив записывается значение 2, если забронирован - 1, в противном случае - 0. Определить номера мест, на которые чаще всего продаются билеты. 

Входные данные 
В первой строке задаются числа N и M (0 <= N, M <= 25). Далее идет N строк по M чисел в каждой. Каждое число может быть равно 0, 1 или 2.

Выходные данные
Выведите на экран номера всех мест (в одну строку, через один пробел), которые продаются чаще всего (выводить номера в порядке возрастания).

Примеры

ID 37095. 37095

В зрительном зале N рядов, в каждом из которых по M мест (кресел). Информация о проданных билетах хранится в двумерном массиве, номера строк которого соответствуют номерам рядов, а номера столбцов - номерам мест. Если билет на то или иное место продан, то в массив записывается значение 2, если забронирован - 1, в противном случае - 0. Определить номера мест, которые чаще всего бронируют и/или выкупают зрители. 

Входные данные
В первой строке задаются числа N и M (0<=N, M<=25). Далее идет N строк по M чисел в каждой. Каждое число может быть равно 0, 1 или 2.

Выходные данные
Выведите на экран номера всех мест (в одну строку, через один пробел), которые продаются или бронируются чаще всего (нумерация мест начинается с 1). Номера выводить в порядке возрастания.
 

Примеры

ID 37094. 12.98а

Информация о количестве жильцов в каждой из M квартир каждого этажа 12-этажного дома хранится в двумерном массиве (в нулевой строке - информация о квартира первого этажа, в первой - второго и т.д.). Определите на каком этаже проживаем меньше всего людей. Выведите это количество и номера всех таких этажей.

Входные данные:  в первой строке подается число M (0<M<=25)
Далее идут 12 строк по M чисел в каждой (целое число, не превосходящее 10)
Выходные данные: выведите на экран сначала требуемое количество людей, затем с новой строки через пробел номера всех таких этажей (в порядке возрастания)
 

ID 37093. 12.98б

Информация о количестве жильцов в каждой из M квартир каждого этажа 12-этажного дома хранится в двумерном массиве (в нулевой строке - информация о квартира первого этажа, в первой - второго и т.д.). Определите на каком этаже проживает больше всего людей. Выведите это количество и номера всех таких этажей.

Входные данные:  в первой строке подается число M (0<M<=25)
Далее идут 12 строк по M чисел в каждой (целое число, не превосходящее 10)
Выходные данные: выведите на экран сначала требуемое количество людей, затем с новой строки через пробел номера всех таких этажей (в порядке возрастания)

Примеры

ID 6031. Поиск требуемой строки - 2

В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Побеждает спортсмен, у которого максимален наилучший бросок. Если таких несколько, то из них побеждает тот, у которого наилучшая сумма результатов по всем попыткам. Если и таких несколько, победителем считается спортсмен с минимальным номером. Определите номер победителя соревнований.

Входные данные: Программа получает на вход два числа n и m (20<=n,m<=20), являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.

Выходные данные: Программа должна вывести одно число - номер победителя соревнований. Не забудьте, что  строки  (спортсмены) нумеруются с 0.

ID 23390. Под побочной диаганалью

Дан двумерный массив размером nxn (n<=10). Сформировать одномерный массив из элементов заданного массива, расположенных под побочной диагональю.

Входные данные 
Программа получает на вход число n <= 10, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по n чисел, являющихся элементами массива.
 

Выходные данные 
Программа должна вывести одномерный массив, элементами которого являются значения элементов двумерного массива (через пробел), расположенные ПОД побочной диагональю.
 

Примеры

ID 23389. Под главной диагональю

Дан двумерный массив размером nxn (n<=10). Сформировать одномерный массив из элементов заданного массива, расположенных под главной диагональю.

Входные данные 
Программа получает на вход число n <= 10, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по n чисел, являющихся элементами массива.
 

Выходные данные 
Программа должна вывести одномерный массив, элементами которого являются значения элементов двумерного массива (через пробел), расположенные ПОД главной диагональю.

Примеры

ID 23388. Над побочной диагональю

Дан двумерный массив размером nxn (n<=10). Сформировать одномерный массив из элементов заданного массива, расположенных над побочной диагональю.

Входные данные 
Программа получает на вход число n <= 10, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по n чисел, являющихся элементами массива.

Выходные данные 
Программа должна вывести одномерный массив, элементами которого являются значения элементов двумерного массива (через пробел), расположенные НАД побочной диагональю.  

Примеры

ID 23387. Над главной диагональю

Дан двумерный массив размером nxn (n<=10). Сформировать одномерный массив из элементов заданного массива, расположенных над главной диагональю.

Входные данные 
Программа получает на вход число n <= 10, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по n чисел, являющихся элементами массива.

Выходные данные
 Программа должна вывести одномерный массив, элементами которого являются значения элементов двумерного массива (через пробел), расположенные НАД главной диагональю.

Примеры

ID 42441. Третья планета от Солнца

На третью планету от Солнца отправили n космических кораблей для сбора различных объектов для изучения. На каждом корабле было размещено по m контейнеров различного объема. После изучения планеты, отобрано n·m экземпляров. Командный состав решил взять несколько экземпляров самого большого объема. Необходимо определить какой объем должен иметь самый большой экземпляр, чтобы его можно было вывезти с планеты, а также количество кораблей и их номера, на которые можно поместить самые большие экземпляры. Все корабли пронумерованы, начиная с нуля.

Входные данные
Первая строка содержит два целых числа n и m: n - количество кораблей, отправленных на третью планету (1 <= n <= 100), m - количество контейнеров на каждом корабле. В следующих n строках содержат по m чисел, каждое из которых показывает объем контейнера (1 <= m <= 100, каждое число - неотрицательное не более 100). 

Выходные данные
Выведите в первой строке - количество космических кораблей, которыми можно привезти самый большой экземпляр, через пробел максимальный объем, который можно вывезти с планеты. На следующей строке выведите через пробел номера кораблей (нумеруются с нуля), на которые можно загрузить самый большой экземпляр.
 

Примеры

3 3
1 2 3
3 5 4
5 2 2

2 5
1 2

ID 42449. Заполнение спиралью

Даны число n. Создайте массив A[2*n+1][2*n+1] и заполните его по спирали, начиная с числа 0 в центральной клетке A[n+1][n+1]. Спираль выходит вверх, далее закручивается против часовой стрелки.

Формат входных данных
Программа получает на вход число  n.

Формат выходных данных
Программа должна вывести полученный массив. Каждый элемент массива необходимо записывать в трех знакоместах.
 

Примеры

 12 11 10  9 24
 13  2  1  8 23
 14  3  0  7 22
 15  4  5  6 21
 16 17 18 19 20

ID 22012. Максимальная строка

ID 44602. Двумерный вектор

Создайте двумерный массив размером n×m и заполните его натуральными числами от 1 до nxm по вертикали (см. пример).

Входные данные

Даны два натуральных числа: n и m, не превышающие 10¹⁰.

Выходные данные

Выведите заполненный двумерный массив

 

Примеры

3 4

1 4 7 10 
2 5 8 11 
3 6 9 12 

ID 44616. Седловая точка

Седловая точка – это элемент матрицы, который одновременно является наибольшим в своем столбце и наименьшим в своей строке. Напишите программу, которая находит индексы всех седловых точек матрицы. Нумерация строк и столбцов матрицы начинается с единицы.

В первой строке записаны через пробел размеры прямоугольной матрицы N и N (количество строк и количество столбцов, 1  <= N, M <=  100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами.
 

Программа должна вывести индексы всех седловых точек матрицы в порядке обхода по строкам (сверху вниз, слева направо). Номер строки и номер столбца каждой седловой точки разделяются пробелами. Нумерация начинается с единицы. Если в матрице нет ни одной седловой точки, нужно вывести число 0.

Примеры

4 5
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
9 17 18 19 20

3 1

ID 44617. Сортировка строк

Напишите программу, которая переставляет строки матрицы так, чтобы значения в столбце K шли в порядке убывания. Строки, у которых значения в столбце K равны, должны быть выведены в том же порядке, в котором они стояли в исходной матрице.
 

В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M ( 1 <= N , M <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами. В последней строке вводится номер столбца K .
 

Программа должна вывести получившуюся матрицу, в которой строки переставлены так, чтобы значения в столбце K шли в порядке убывания.
 

Примеры

4 5
21 22 23 24 25
26 12 18 29 33
11 37 31 14 39
16 17 18 5 20
1

26 12 18 29 33 
21 22 23 24 25 
16 17 18 5 20 
11 37 31 14 39 

ID 44618. Цветовое преобразование

Яркости пикселей рисунка закодированы числами от 0 до 255 в виде матрицы. Преобразовать рисунок в черно-белый по следующему алгоритму:

1. вычислить среднюю яркость пикселей по всему рисунку
2. все пиксели, яркость которых меньше средней, сделать черными (записать код 0), а остальные -– белыми (код 255)

Входные данные

В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M ( 1 <= N , M <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел в диапазоне от 0 до 255, разделённых пробелами.
 

Программа должна вывести в первой строчке среднее значение яркости для заданного рисунка с точностью 4 знака в дробной части. В следующих N строчках выводится построенная матрица, соответствующая чёрно-белому изображению.

Примеры

4 4
12 14 67 45
32 87 45 63
69 45 14 11
40 12 35 15

37.8750
0 0 255 255
0 255 255 255
255 255 0 0
255 0 0 0

ID 44677. Посещение театра

Учащиеся театрального кружка школы любят посещать театр. В очередной раз они пошли в театр, в котором n рядов по m мест в каждом. Руководитель кружка пришла за билетами и хочет купить билеты всем учащимся в одном ряду на соседние места. 
По имеющейся информации о проданных билетах на спектакль определите, сможет ли руководитель купить билеты всем учащимся и себе в одном ряду. 
Информация о проданных билетах записана в двумерный массив (единицы означают, что на данное место билет продан, ноль - что место свободно). Руководителю кружка вместе с детьми необходимо k билетов.

В первой строке входных данных находятся числа n, m, k <= 100. В следующих n строках входных данных расположены по m чисел (0 и 1), разделенных пробелами.

Выведите YES или NO в зависимости от ответа на вопрос задачи.

Примеры

3 4 2
0 1 0 1
1 0 0 1
1 1 1 1

YES

ID 44711. Путешествие ферзя

Алиса часто играет в шахматы. Причем так как она любит путешествовать по другим галактикам, она знает много разновидностей этой древней игры.  Иногда она просто решает головоломки, созданные на шахматной доске.  Шахматная доска Алисы может иметь самые разные размеры, не только 8×8.

4 4 7
10 20 0 100
30 0 0 40
0 0 0 0
45 42 0 70

1 2 0 8 
3 0 0 4 
0 0 0 0 
6 5 0 7 

2 4 4
10 20 30 40
0 50 0 0

Wrong Board

2 2 2
1 2
4 3

Wrong Board

ID 44712. Ральф любит пончики

Громила Ральф вот уже 30 лет живёт в игровом автомате, и вы его можете увидеть на экране того самого автомата. 
Сегодня Ральф гуляет по экрану, на котором отображается прямоугольное изображение, разбитое на N x N клеток. В каждой клетке находится тарелка с его любимыми блинчиками (на всех тарелках разное количество блинчиков). Ральф начинает перемещаться с левой нижней клетки прямоугольника. Съев все блинчики в текущей клетке, он перемещается на одну клетку вправо или на одну клетку вверх, всегда выбирая ту из клеток, где больше блинчиков в тарелке (за пределами прямоугольника тарелок с блинчиками нет). В конце концов Ральф приходит в правую верхнюю клетку. Вам же предстоит определить, сколко всего блинчиков съел Ральф пока путешествовал по экрану. Блинчики в начальной и конечной клетках Ральф тоже съел с большим удовольствием.

Программа получает на вход в первой строке целое число N – размер изображения (2 <= N <= 10). В следующих N строках задаются через пробел числа, обозначающие количество блинчиков на тарелках, начиная с верхнего ряда и заканчивая нижним. Все числа – различные, натуральные, не превосходящие 100.

Выведите одно число - количество блинчиков, которое съест Ральф, добравшись до правой верхней клетки.

 

Примеры

2
37 82
23 52

157

ID 44715. Параллельное программирование

Миша занимается параллельным программированием. Сегодня он пишет программу для исполнителя "Квадратик". Исполнитель "Квадратик" живет на клетчатом поле размера  N х M, размер одной клетки 1х1. Перемещаясь он закрашивает клетку, на которой побывал. Клетку, на которой он начал движение и на которой остановился он также закрашивает. 
Миша установил на поле K "Квадратиков". Каждый "Квадратик" будет двигаться в указанном Мишей направлении и останавливаться дойдя до конца поля. После окончании движения всех "Квадратиков", Миша хочет узнать сколько клеток поля получились закрашенными. Так как задача подсчета не относится к параллельному программированию, а размер поля может быть очень большим, Миша попросил вас написать программу для подсчета таких клеток.
 

Программа получает на вход несколько строк. Первая строка содержит целые числа M и N - размеры поля исполнителя "Квадратик" (1 <= M, N <= 10⁶). Во второй строке записано число K - количество "Квадратиков" на поле (0 <= K <= 10³). Далее идут K строк, каждая из которых описывает положение определенного "Квадратика" и направление, в котором он будет перемещаться. Формат каждой из таких строк: два целых числа, записанных через один пробел и один символ  {N, E, S, W} - начальные координаты и направление движения соответствующего "Квадратика". Символ отделен от чисел ровно одним пробелом. 
Символами обозначены следующие направления движения: N - вверх, S - вниз, W - влево, Е - вправо.

Выведите количество закрашенных клеток поля, после окончания движения всех "Квадратиков".


Пояснения
Поле исполнителя и расположение "Квадратиков" для первого примера, показаны на рисунке ниже. Стрелочкой обозначено направление движения соответствующего "Квадратика".

Примеры

8 5
4
4 4 S
6 2 W
6 3 N
6 4 S

13

ID 26981. 2048

Входные данные

Выходные данные

Примеры

2 0 0 0
2 0 0 0
2 0 0 0
0 0 0 0

4

2 0 0 0
2 0 0 0
2 0 0 0
2 0 0 0

8

2 2 4 0
0 0 0 0
0 0 0 0
0 0 0 0

4

2 2 4 0
0 2 2 2
0 2 4 0
2 4 4 0

16

Примечания

ID 18783. Диагональки

Примеры

ID 22007. Вытаскивание минимума

Примеры

ID 18788. Хождение за золотом - 1

Примеры

ID 18789. Хождение за золотом - 2

Однажды царь решил вознаградить одного из своих мудрецов за хорошую работу. Он привел его в прямоугольную комнату размром NxM, в каждой клетке которой лежало несколько килограммов золота. Царь разрешил мудрецу сделать обойти несколько клеток (переходя с клетки, где сейчас находится мудрец, в одну из четырех с ней соседних), и собрать все золото, которое попадется на его пути.
Мудрецу разрешено более одного раза проходить по одной и той же клетке. Золото с нее он берет при этом  только один раз - когда проходит по клетке в первый раз.

Вам дан маршрут мудреца. Требуется определить, сколько килограммов золота он собрал.

Входные данные
Входные данные содержат план комнаты и маршрут мудреца. Сначала записано количество строк N, затем - количество столбцов M (1<=N<=20,1<=M<=20).
Затем записано N строк по M чисел в каждой - количество килограммов золота, которое лежит в данной клетке (число от 0 до 50).
Далее записано число X - сколько клеток обошел мудрец. Далее записаны координаты этих клеток (координаты клетки - это два числа: первое определяет номер строки, второе - номер столбца, верхняя левая клетка на плане имеет координаты (1,1), правая нижняя - (N,M)). 

Примеры

ID 22014. Хождение за золотом - 3

Примеры

ID 44942. Сумма положительных и отрицательных

Дан двумерный массив A размерностью NxM. Напишите программу, которая добавляет к элементам каждой строки такой новый элемент, чтобы сумма положительных элементов строки стала бы равна модулю суммы отрицательных элементов строки.

Входные данные
В первой строке входных данных записаны через один пробел два натуральных числа N и M ( 0 < N, M <= 25). Далее идут N строк по M положительных целых чисел в каждой - элементы матрицы A (каждый элемент матрицы не превышает 10⁵).

Выходные данные
Выведите результирующий массив A размерностью Nx(M+1) на экран. Все элементы строки должны быть разделены одним пробелом.
 
 

Примеры

ID 45716. Сортировка главной диагонали

Напишите программу, которая переставляет элементы квадратной матрицы, расположенные на главной диагонали, в порядке возрастания. Остальные элементы матрицы должны остаться на своих местах.
 

В первой строке записано одно число N размер квадратной матрицы ( 1 <= N <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по N натуральных чисел, разделённых пробелами. 
 

Программа должна вывести получившуюся матрицу, в которой элементы главной диагонали расположены в порядке возрастаниия.
 

Примеры

5
1 11 11 5 10 
2 9 2 10 2 
12 9 10 9 15 
6 15 14 1 11 
11 12 4 9 3 

1 11 11 5 10 
2 1 2 10 2 
12 9 3 9 15 
6 15 14 9 11 
11 12 4 9 10

ID 45717. Сортировка побочной диагонали

Напишите программу, которая переставляет элементы квадратной матрицы, расположенные на побочной диагонали, в порядке убывания, начиная с правого верхнего угла. Остальные элементы матрицы должны остаться на своих местах.
 

В первой строке записано одно число N размер квадратной матрицы ( 1 <= N <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по N натуральных чисел, разделённых пробелами. 
 

Программа должна вывести получившуюся матрицу, в которой элементы побочной диагонали расположены в порядке возрастаниия.
 

Примеры

5
12 4 8 13 13 
1 12 1 4 15 
2 3 5 2 3 
6 5 13 12 14 
14 9 15 4 12 

12 4 8 13 14 
1 12 1 13 15 
2 3 5 2 3 
6 5 13 12 14 
4 9 15 4 12

ID 45719. Сортировка двумерного массива

Напишите программу, которая сортирует двумерный массив целых чисел. При этом самое маленькое число должно оказаться в первом элементе первой строки, а самое большое в последнем элементе последней строки.

В первой строке записаны через пробел размеры двумерного массива: количество строк N и количество столбцов M ( 1 <= N , M <= 100 ). В следующих N строках записаны строки двумерного массива, в каждой – по M натуральных чисел, разделённых пробелами. 
 

Программа должна вывести отсортированный двумерный массив.
 

Примеры

5 7
13 5 1 8 4 14 5 
5 13 10 9 3 7 7 
3 3 9 6 3 7 5 
10 8 11 2 1 1 13 
1 12 13 15 9 11 4 

1 1 1 1 2 3 3 
3 3 4 4 5 5 5 
5 6 7 7 7 8 8 
9 9 9 10 10 11 11 
12 13 13 13 13 14 15 

ID 38577. Перекраска клеток

Дано клетчатое поле N x M, все клетки поля изначально белые. Автомат умеет:

закрасить клетку (i,j) в черный цвет.
для клетки (i,j) узнать её ближайших белых соседей по вертикали и горизонтали.
Дана последовательность команд для автомата. Требуется выполнить эти команды в указанной последовательности, и для каждой команды запроса ближайших белых соседей указать результат ее выполнения.

Входные данные
Сначала вводятся размеры поля N и M (1 ≤ N ≤ 20, 1 ≤ M ≤ 50000), затем количество команд K (1 ≤ K ≤ 10⁵), а затем сами команды. Команды записаны по одной в строке в следующем формате:

Color i j — окраска клетки (i,j) в черный цвет;
Neighbors i j — нахождение белых соседей для БЕЛОЙ клетки (i,j).

1 ≤ i ≤ N, 1 ≤ j ≤ M.

Выходные данные
На каждый запрос Neighbors требуется вывести сначала количество ближайших белых соседей (или 0, если ни с одной из сторон белых клеток не осталось), а затем их координаты (соседей можно перечислять в произвольном порядке). Если запросов Neighbors нет, ничего выводить не надо.

Примеры

ID 21821. Крестики-нолики

...
000
XXX
...
...

..0.
.XX0
.0X.
....

......
.XXX..
.0000.
..X...
......

ID 27043. Пираты!

Пример одного из безопасных маршрутов показан на рисун ке. Пиратские базы обозначены чјрным, клетки маршрута серым. Минимальное расстояние от пиратской базы до маршрута 3 хода.

ID 23368. Организация конференции (С, B')

ID 27225. Modern Art #3

ID 27301. Building a Ski Course

ID 47972. Вывод столбца

Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают 50.
Далее идет число k (1<=k<=N) 

Формат выходных данных
Вывести на экран k-й столбец (считая, что нумерация элементов массива начинается с 1, т.е. для первого столбца k=1).
Все элементы выводить в одну строку через 1 пробел между элементами.

ID 48043. min/max в матрице - 1

Дана матрица numsi,j размером nxm. Заменить каждый элемент матрицы, оканчивающийся на 12, на минимальный элемент матрицы. 

Формат входных данных
Программа получает на вход в первой строке два числа n, m - количество строк и столбцов в матрице. В каждой из следующих n+1 строке записаны по m чисел - элементы матрицы numsi,j. (1<= n, m <= 15, -10⁵ <= numsi,j<=10⁵)

Формат выходных данных
Выведите измененную матрицу на экран. Элементы в строке должны разделяться одним пробелом.
 

ID 48044. min/max в матрице - 2

Дана матрица numsi,j размером nxm. Заменить каждый элемент матрицы, оканчивающийся на 43, на максимальный элемент матрицы. 

Формат входных данных
Программа получает на вход в первой строке два числа n, m - количество строк и столбцов в матрице. В каждой из следующих n+1 строке записаны по m чисел - элементы матрицы numsi,j. (1<= n, m <= 15, -10⁵ <= numsi,j<=10⁵)

Формат выходных данных
Выведите измененную матрицу на экран. Элементы в троке должны разделяться одним пробелом.
 

ID 48045. Строки с min/max

Дана матрица numsi,j размером nxm. Вывести те строки матрицы, в которых имеется хотя бы один элемент, равный минимальному элементу матрицы.

Формат входных данных
Программа получает на вход в первой строке два числа n, m - количество строк и столбцов в матрице. В каждой из следующих n+1 строке записаны по m чисел - элементы матрицы numsi,j. (1<= n, m <= 15, -10⁵ <= numsi,j<=10⁵)

Формат выходных данных
Выведите строки матрицы, которые удовлетворяют условию задачи. Строки необходимо выводить в том же порядке, в котором они записаны в матрице.

ID 48047. Столбцы с min/max

Дана матрица numsi,j размером nxm. Вывести те столбцы матрицы, в которых имеется хотя бы один элемент, равный минимальному элементу матрицы.

Формат входных данных
Программа получает на вход в первой строке два числа n, m - количество строк и столбцов в матрице. В каждой из следующих n+1 строке записаны по m чисел - элементы матрицы numsi,j. (1<= n, m <= 15, -10⁵ <= numsi,j<=10⁵)

Формат выходных данных
Выведите столбцы матрицы, которые удовлетворяют условию задачи. Элементы столбцов необходимо выводить в одной строке, столбцы выводить в том же порядке, в котором они записаны в матрице.

ID 48128. Бинарная картина для Алисы

Дед Мороз принёс Алисе новогодний подарок - Бинарную картину, которая представляет собой матрицу размером n x n, где каждое значение равно 0 или 1. Однако, перед тем как положить его под елку, Дед Мороз заметил, что полученная картина немного отличается от той, которую она заказывала.

Чтобы получить картинку, которую хотела Алиса, нужно выполнить следующие два шага:

1. Отразить картинку горизонтально: перевернуть каждую строку матрицы.
2. Инвертировать каждый пиксель: заменить каждое значение 0 на 1 и каждое значение 1 на 0.

У Деда Мороза осталось совсем немного времени, чтобы изменить ошибочную картину. Для этого необходимо просто записать в его волшебный посох программу, которая бы изменила текущую.

Помогите Деду Морозу написать программу для посоха, иначе дети могут остаться без новогодних подарков!

Формат входных данных
Программа получает на вход в первой строке число n - размер картины (1 <= n <= 20). В каждой из следующих n строк написано по n чисел 0 или 1. 

Формат выходных данных
Выведите бинарную картину, которую хотела получить на Новый год Алиса. Элементы в строке разделяются одним пробелом.
 

ID 47514. Максимальный в области 1

Напишите программу, которая выводит максимальный элемент в заштрихованной области квадратной матрицы.

ID 49391. Магический квадрат подрядка N

Формат входных данных
В первой строке вводится размер матрицы N (0 < N <= 100). В следующих N строках вводятся строки матрицы, по N значений в каждой, разделённые пробелами.
 

Формат выходных данных
Программа должна вывести слово 'YES', если матрица является магическим квадратом, и слово 'NO', если не является.

ID 30719. Вирус

В лаборатории биоинформатики ученые проводят эксперименты по распространению искусственно созданных вирусов. Для эксперимента используется специальная лабораторная установка, представляющая собой таблицу из n × m ячеек. В каждую ячейку помещается живая клетка. Ученые заражают вирусом некоторые клетки, всего исходно заражается не более 8 клеток.
Каждую секунду среди незараженных клеток, имеющих зараженную клетку в соседней по стороне ячейке, ровно одна клетка заражается вирусом.
Ученые заинтересовались, какие конфигурации зараженных клеток могут получиться через t секунд. Для начала они хотят посчитать число таких конфигураций. Помогите им это сделать.

Формат входных данных
В первой строке входного файла находятся целые числа n, m и t (1 ≤ n, m ≤ 100, 1 ≤ t ≤ 6) — размеры таблицы и количество секунд. Каждая из следющих n строк содержит m символов. Символ «.» означает, что в изначальной конфигурации клетка не заражена, а символ «*» — что заражена. Количество «*» в таблице не превышает 8. Гарантируется, что незараженных клеток в исходной конфигурации не меньше t.

Формат выходных данных
Выведите количество различных возможных конфигураций таблицы после t секунд.
 

ID 49712. Сортировка строк

Напишите программу, которая переставляет строки матрицы так, чтобы значения в столбце K шли в порядке убывания. Строки, у которых значения в столбце K равны, должны быть выведены в том же порядке, в котором они стояли в исходной матрице.
 

В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M ( 1 <= N , M <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами. В последней строке вводится номер столбца K .
 

Программа должна вывести получившуюся матрицу, в которой строки переставлены так, чтобы значения в столбце K шли в порядке убывания.
 

Примеры

4 5
21 22 23 24 25
26 12 18 29 33
11 37 31 14 39
16 17 18 5 20
1

26 12 18 29 33 
21 22 23 24 25 
16 17 18 5 20 
11 37 31 14 39 

ID 50273. Изображение перекрестка

Необходимо изобразить в текстовом формате перекресток двух дорог.

Изображение должно иметь размер \(n \times n\), ширина дорог должна быть \(l\). Центр перекрестка должен быть в центре изображения. Для клеток дороги следует использовать символ <<*>>, для клеток вне дороги символ <<.>>.

Формат входных данных
На первой строке дано целое число \(n\). На второй строке дано первое число \(l\). (\(3 \le n \le 100\), \(1 \le l < n\), \(l\) и \(n\) имеют одинаковую четность)

Формат выходных данных
Выведите \(n\) строк, изображение перекрестка.

ID 50573. Рамки

Сеня решил написать операционную систему. Для начала он планирует написать подпрограмму, которая будет рисовать рамки окон.

Поле для рисования представляет собой прямоугольник \(h \times w\) пикселей, строки занумерованы сверху вниз от 1 до \(h\), столбцы — слева направо от 1 до \(w\).

На поле последовательно рисуются \(n\) рамок, \(i\)-я рамка представляет собой границы прямоугольника с противоположными углами в точках \((r_{i,1}, c_{i,1})\) и \((r_{i,2}, c_{i,2})\).

Требуется вывести получившееся изображение в виде \(h\) рядов по \(w\) символов, пискель, который не был использован при изображении рамок, следует вывести с использованием символа <<.>>, а пиксели \(i\)-й рамки с использованием \(i\)-го символа латинского алфавита (первая рамка изображается буквами <<a>>, вторая — <<b>>, и т.д.)

Формат входных данных
Первая строка содержит целые числа \(h\), \(w\) и \(n\) — размеры поля и число рамок (\(2 \le h, w \le 80\), \(1 \le n \le 26\)). Следующие \(n\) строк содержат по четыре целых числа каждая: \(r_{i,1}, c_{i,1}, r_{i,2}\) и \(c_{i,2}\) (\(1 \le r_{i,1} < r_{i,2} \le h\),. \(1 \le c_{i,1} < c_{i,2} \le w\)).

Формат выходных данных
Выведите результат вывода описанных во вводе рамок.

ID 50951. Подматрица - 2

У Фили есть квадратная матрица \(A\) размера \(N \times N\), но она кажется ему слишком большой. Ему гораздо больше нравятся матрицы размера \(k \times k\) (\(k < N\)).

Филя хочет получить матрицу нужного размера взяв некоторую подматрицу исходной матрицы. Подматрицей \(k \times k\) матрицы \(A\) в данном случае Филя считает матрицу \(B\) такую, что \(b_{i, j} = a_{i + x, j + y}\), для всех \(i\), \(j\) от \(1\) до \(k\). Из данного определения можно заметить, что подматрица исходной матрицы задается парой чисел (\(x\), \(y\)).

Для того, чтобы выбрать наиболее интересную для себя подматрицу, Филя хочет узнать, сколько есть способов выбрать из исходной матрицы две различные (характеризующие пары (\(x\), \(y\)) отличаются хотя бы в одной позиции) неравные подматрицы \(k \times k\). Две матрицы \(Q\) и \(P\) размера \(k \times k\) считаются равными, если для любых \(i, j: 1 \le i, j \le k\) выполняется \(q_{i, j} = p_{i, j}\). Если условия равенства не выполняется, матрицы считаются неравными.

Формат входных данных
В первой строке входного файла содержатся два натуральных числа \(N\) и \(k\) — размеры исходной и нужной матрицы. (\(1 \le k < N \le 10\)). В следующих \(N\) строках заданы через пробел по \(N\) натуральных чисел \(a_{i, j}\) — элементы исходной матрицы (\(1 \le a_{i, j} < 10\)).

Формат выходных данных
В единственной строке выходного файла выведите одно число — количество способов выбрать из исходной матрицы две различные неравные подматрицы размера \(k \times k\).

ID 37069. Подматрица - 1

У Фили есть квадратная матрица \(A\) размера \(N \times N\), но она кажется ему слишком большой. Ему гораздо больше нравятся матрицы размера \(k \times k\) (\(k < N\)).

Филя хочет получить матрицу нужного размера взяв некоторую подматрицу исходной матрицы. Подматрицей \(k \times k\) матрицы \(A\) в данном случае Филя считает матрицу \(B\) такую, что \(b_{i, j} = a_{i + x, j + y}\), для всех \(i\), \(j\) от \(1\) до \(k\). Из данного определения можно заметить, что подматрица исходной матрицы задается парой чисел (\(x\), \(y\)).

Для того, чтобы выбрать наиболее интересную для себя подматрицу, Филя хочет узнать, сколько есть способов выбрать из исходной матрицы две различные (характеризующие пары (\(x\), \(y\)) отличаются хотя бы в одной позиции) равные подматрицы \(k \times k\). Две матрицы \(Q\) и \(P\) размера \(k \times k\) считаются равными, если для любых \(i, j: 1 \le i, j \le k\) выполняется \(q_{i, j} = p_{i, j}\). Если условия равенства не выполняется, матрицы считаются неравными.

Формат входных данных
В первой строке входного файла содержатся два натуральных числа \(N\) и \(k\) — размеры исходной и нужной матрицы. (\(1 \le k < N \le 10\)). В следующих \(N\) строках заданы через пробел по \(N\) натуральных чисел \(a_{i, j}\) — элементы исходной матрицы (\(1 \le a_{i, j} < 10\)).

Формат выходных данных
В единственной строке выходного файла выведите одно число — количество способов выбрать из исходной матрицы две различные равные подматрицы размера \(k \times k\).

ID 53795. Состязания - 2

В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Победителем соревнований объявляется тот спортсмен, у которого максимален наилучший результат по всем броскам. Таким образом, программа должна найти значение максимального элемента в данном массиве, а также его индексы (то есть номер спортсмена и номер попытки).

Входные данные
Программа получает на вход два числа n и m, являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.

Выходные данные
Программа выводит значение максимального элемента, затем номер строки и номер столбца, в котором он встречается. Если в массиве несколько максимальных элементов, то нужно вывести минимальный номер строки, в которой встречается такой элемент, а если в этой строке таких элементов несколько, то нужно вывести минимальный номер столбца. Не забудьте, что все строки и столбцы нумеруются с 0.

ID 53799. Состязания - 3

В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Побеждает спортсмен, у которого максимален наилучший бросок. Если таких несколько, то из них побеждает тот, у которого наилучшая сумма результатов по всем попыткам. Если и таких несколько, победителем считается спортсмен с минимальным номером. Определите номер победителя соревнований.

Входные данные
Программа получает на вход два числа n и m, являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.

Выходные данные
Программа должна вывести одно число - номер победителя соревнований. Не забудьте, что  строки  (спортсмены) нумеруются с 0.

ID 53801. Заполнение диагоналями

Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.

Входные данные
Программа получает на вход два числа n и m.

Выходные данные
Программа должна вывести  полученный массив.

ID 53906. Цифровое табло

В комнате у Аркадия Семеновича Тапкина стоят электронные часы. Цифры на этих часах показываются в специальной псевдографике. А именно каждое поле, на котором изображается цифра, состоит из \(w\) ячеек в ширину и \(h\) ячеек в высоту (при этом ячейки на поле имеют форму квадратов).

Но недавно у Аркадия Семеновича появилась проблема. Последнее время он стал плохо видеть. В связи с этим он хочет увеличить изображение этих цифр. Он уже приладил старый \(19''\) монитор к часам, и теперь дело осталось за малым. Осталось написать программу, которая будет рисовать цифры на дисплее. Аркадий Семенович хочет увеличить изображение в \(k\) раз и сделать толщину линий равной \(d\). Помогите ему в этом.

Опишем более формально понятие <<увеличить в \(k\) раз>>. Занумеруем ячейки поля \(w \times h\) сверху вниз и слева направо. Таким образом, верхняя левая ячейка имеет координаты \((0, 0)\), правая нижняя — \((w - 1, h - 1)\), правая верхняя — \((w - 1, 0)\), левая нижняя — \((0, h - 1)\). Кроме этого, введем декартову прямоугольную систему координат так, что начало координат находится в центре верхней левой ячейки, ось \(Ox\) направлена вправо, ось \(Oy\) — вниз, длину единичного отрезка примем равной длине стороны ячейки. Таким образом, координаты центра ячейки совпадают с ее координатами во введенной нумерации.

Каждая десятичная цифра задается набором составляющих ее изображение отрезков. Для простоты каждый из отрезков либо параллелен одной из координатных осей, либо идет под углом в 45 градусов к ней.

Увеличенная в \(k\) раз цифра рисуется на поле размером \((w - 1) \cdot (k - 1) + w\) ячеек по горизонтали на \((h - 1) \cdot (k - 1) + h\) ячеек по вертикали.

При увеличении некоторой цифры в \(k\) раз производятся следующие операции. Координаты точек, являющихся концами отрезков, составляющих цифру, умножаются на \(k\). После этого закрашиваются те ячейки, через центры которых проходят эти отрезки. Эти ячейки будем называть основными.

После этого, для того, чтобы получить толщину линий равную \(d\), дополнительно закрашиваются те ячейки, центры которых располагаются на расстоянии, не превышающем \((d - 1)\) от центров основных ячеек. Расстоянием между точками \(A(x_A, y_A)\) и \(B(x_B, y_B)\) будем называть число \(\rho(A, B) = |x_A - x_B| + |y_A - y_B|\).

По описанию цифры и параметрам \(k\) и \(d\) выведите изображение цифры, увеличенное в \(k\) раз, с толщиной линий \(d\).

Формат входных данных
Первая строка содержит целые числа \(k\) и \(d\) (\(1 \le k \le 100\), \(1 \le d \le 500\)). Вторая строка содержит целые числа \(w\) и \(h\) (\(1 \le w, h \le 10\)).

Третья строка содержит целое число \(n\) (\(1 \le n \le 100\)) — количество отрезков в описании цифры. Далее следуют \(n\) строк, каждая из которых описывает один отрезок. Описание отрезка состоит из четырех целых чисел: \(x_1\), \(y_1\), \(x_2\), \(y_2\) (\(0 \le x_1, x_2 < w\), \(0 \le y_1, y_2 < h\)) — координат концов отрезка.

Каждый из отрезков либо параллелен одной из координатных осей, либо идет под углом в 45 градусов к ней. Все отрезки имеют ненулевую длину.

Формат выходных данных
Выходные данные должны содержать ровно \((h - 1) \cdot (k - 1) + h\) строк по \((w - 1) \cdot (k - 1) + w\) символов в каждой, \(j\)-ый символ \(i\)-ой строки должен быть равен символу <<*>> (звездочка), если ячейка с центром в точке \((j,i)\) закрашена, и символу <<.>> (точка) — иначе.

ID 54226. Матрица

Дан набор натуральных чисел: a₁, …, a_N. По этому набору строится таблица чисел размером N x N по следующему правилу: в клетку i-го столбца j-й строки записывается большее из чисел a_i и a_j при i ≠ j (если a_i = a_j, то записывается это число); на пересечении i-го столбца и i-й строки записывается число 0.

Дана таблица чисел. Требуется определить, могла ли она быть построена по данным правилам из какого-либо набора чисел a₁, …, a_N.

Входные данные
В первой строке входных данных задается натуральное число N – размер таблицы (1 ≤ N ≤ 500). В следующих N строках содержится по N чисел – числа соответствующей строки из таблицы (все числа целые неотрицательные и не превосходят 1 000).

Выходные данные
В одну строку выведите через пробел числа a₁, …, a_N. Если решений несколько, выведите любое из них. Если набора, удовлетворяющего данной таблице, не существует, выведите одно число "-1".

ID 54282. Жизнь в квадрате

В некоторых клетках квадрата N x N
 живут микроорганизмы (не более одного в одной клетке). Каждую секунду происходит следующее:
– все микроорганизмы, у которых менее 2-х соседей, умирают от скуки (соседями называются микроорганизмы, живущие в клетках, имеющих общую сторону или вершину);
– все микроорганизмы, у которых более 3-х соседей, умирают от перенаселенности;
– на всех пустых клетках, у которых ровно в трех соседних клетках жили микроорганизмы, появляются новые микроорганизмы.
Все изменения происходят одновременно, то есть для каждой клетки сначала выясняется ее судьба, а затем происходят изменения сразу во всех клетках.
Требуется по данной конфигурации определить, во что она превратится через T
 секунд.

Входные данные
В первой строке вводятся два натуральных числа – N (1 ≤ N ≤ 10) и T (1 ≤ T ≤ 100). Далее записано N строчек по N чисел, описывающих начальную конфигурацию (0 – пустая клетка, 1 – микроорганизм). Числа в строках разделены пробелами.

Выходные данные
Требуется вывести N строк по N чисел – описание конфигурации через T секунд (в том же формате, как и во входных данных).

ID 55363. Мурка ест траву

Пастбище представляет собой прямоугольник, разбитый на N  x N  клеток. В каждой клетке растет трава, имеющая свою калорийность (во всех клетках калорийность травы разная). В левой нижней клетке стоит корова Мурка. Съев всю траву в своей клетке, она перемещается на одну клетку вправо или на одну клетку вверх, всегда выбирая ту из клеток, калорийность травы в которой больше (за пределами поля трава не растет). В конце концов корова приходит в правую верхнюю клетку. Требуется определить, сколько всего калорий получит корова (считая калории травы в первой и в последней клетках).

Входные данные
Сначала вводится число N  – размер поля (2 ≤ N  ≤ 10). В следующей строке вводятся через пробел числа, задающие количество калорий в клетках верхнего ряда, в следующей – количество калорий в клетках следующего ряда, …, в последней – количество калорий в клетках нижнего ряда. Все числа – различные, натуральные, не превосходящие 100.

Выходные данные
Требуется вывести количество калорий, которое получит корова.

ID 55387. Монстры

В одной секретной лаборатории вывели новый вид маленьких монстров, размером чуть больше суслика. В ходе исследований ученые решили поставить следующий эксперимент. В центре комнаты устанавливается прямоугольный стол, поверхность которого разбита на N
 х M  клеток размера 1 х 1. В начальный момент времени на некоторых его клетках располагаются монстры, смотрящие параллельно сторонам стола. По команде экспериментатора монстры начинают двигаться по прямой в ту сторону, в которую они смотрят, доходят до края стола и спрыгивают на пол. Там их собирает лаборант Петя и относит в клетку.


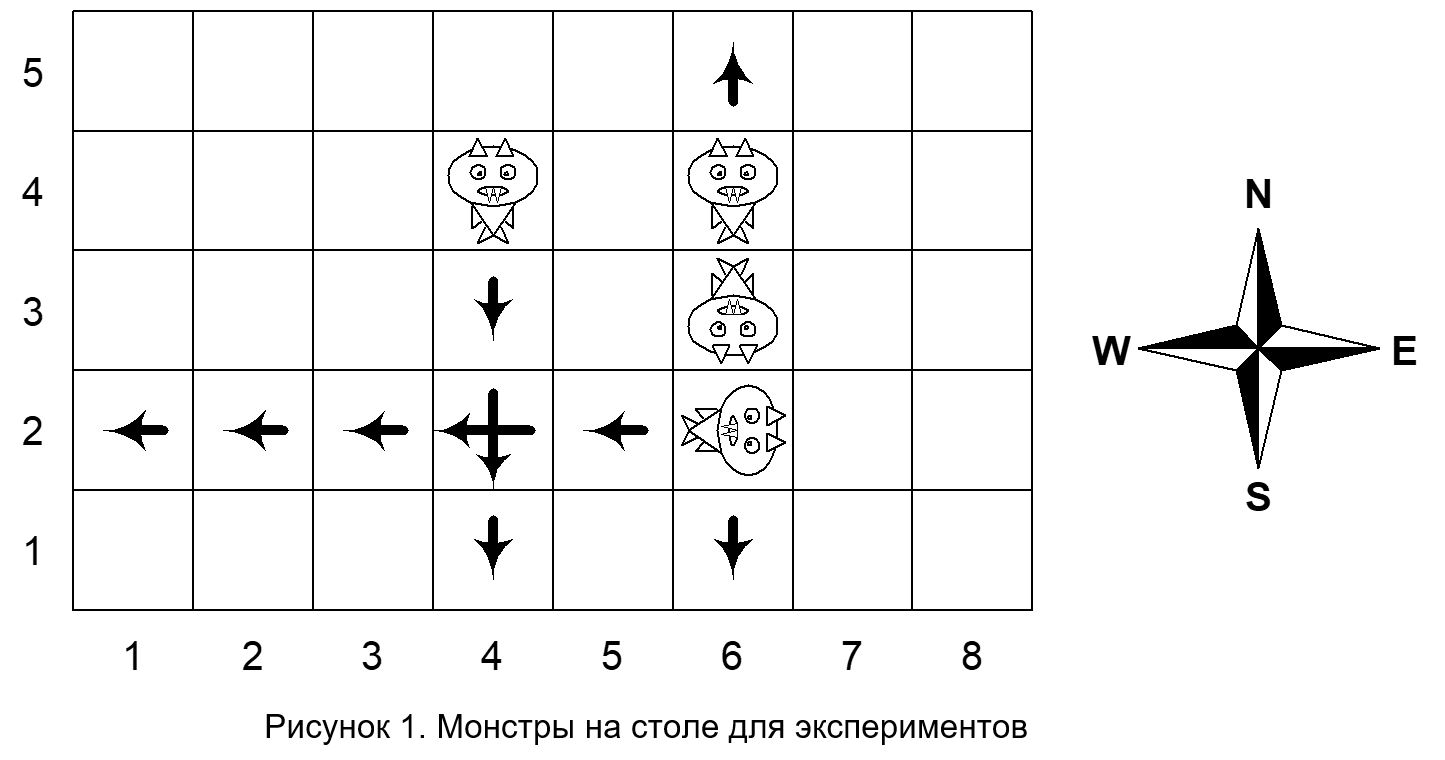
Поскольку у монстров очень грязные лапки, они оставляют следы на тех клетках, на которых они побывали. Так как отмывать стол придется лаборанту Пете, его заинтересовал вопрос - в каком количестве клеток побывают монстры. Помогите ему решить эту сложную задачу.

Программа получает на вход несколько строк. Первая строка содержит целые числа M и N - размеры лабораторного стола (1 <= M, N <= 10⁶). Во второй строке записано число K - количество монстров (0 <= K <= 10³).  Следующие K  строк содержат описания монстров - два целых числа и один символ из множества {N, E , S, W} - начальные координаты и направление соответствующего монстра (соответствие направлений и координат приведено на рисунке 1). Символ отделен от чисел ровно одним пробелом.
Символами обозначены следующие направления движения: N - вверх, S - вниз, W - влево, Е - вправо.

Выведите единственное число - количество клеток стола, на которых побывают монстры.


Пояснения
Поле исполнителя и расположение "Квадратиков" для первого примера, показаны на рисунке ниже. Стрелочкой обозначено направление движения соответствующего "Квадратика".

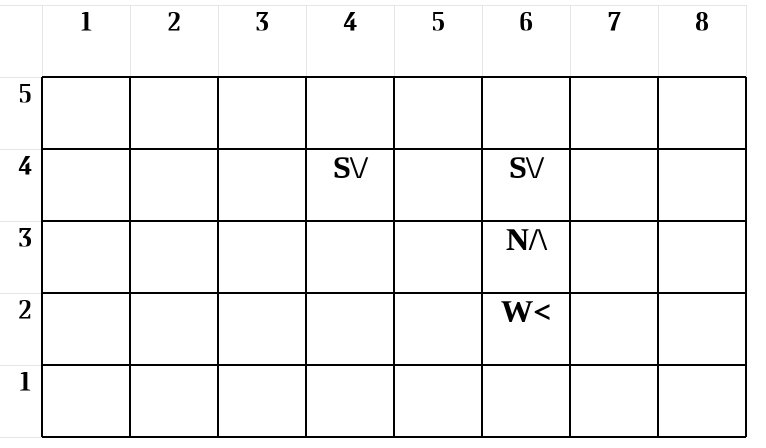
Примеры

8 5
4
4 4 S
6 2 W
6 3 N
6 4 S

13

ID 54509. Столица

В некотором царстве, в некотором государстве было N  городов, и все они, судя по главной карте императора, имели целые координаты. В те годы леса были дремучие, дороги же строить умели только параллельно осям координат, так что расстояние между двумя городами определялось как |x1 - x2| + |y1 - y2|.

Император решил построить N+1-ый город и сделать его столицей своего государства, при этом координаты столицы также должны быть целыми. Место для столицы следует выбрать так, чтобы среднее арифметическое расстояний между столицей и остальными городами было как можно меньше. Однако, разумеется, столицу нельзя строить на месте существующего города.

Нелегкая задача выбрать место для столицы поручена Вам.

Входные данные
В первой строке вводится число N - количество городов (1 <= N <= 100). Следующие N строк содержат координаты городов - пары целых чисел, не превышающих 1000 по абсолютной величине.

Выходные данные
Выведите два целых числа - координаты точки, где следует построить столицу. Если решений несколько, выведите любое.

ID 54668. Блокада

Государство Флатландия представляет собой прямоугольник размером M × N, состоящий из единичных квадратиков. Флатландия разделена на K провинций (2 <= K <= 100). Каждая провинция представляет собой связное множество квадратиков, т.е. из каждой точки провинции можно дойти до любой другой ее точки, при этом разрешается переходить с квадратика на квадратик, только если они имеют общую сторону (общей вершины недостаточно). Во Флатландии нет точки, которая граничила бы более чем с тремя провинциями (т.е. четыре квадратика, имеющие общую вершину, не могут принадлежать четырем разным провинциям).

Каждая провинция имеет свой символ. Столица Флатландии находится в провинции, которой принадлежит символ A (заглавная латинская буква A). Провинция называется пограничной, если она содержит граничные квадратики. Провинция, в которой находится столица Флатландии, не является пограничной.

Король соседнего с Флатландией королевства Ректилания решил завоевать Флатландию. Для этого он хочет захватить столицу Флатландии. Однако он знает, что сил его армии недостаточно, чтобы сделать это сразу. Поэтому сначала он хочет окружить столичную провинцию, чтобы ослабить силы противника долгой блокадой, а потом захватить столицу.

Чтобы окружить провинцию, требуется захватить все провинции, с которыми она граничит. Две провинции граничат, если существует два квадратика, имеющие общую сторону, один из которых принадлежит первой из них, а другой - второй. Чтобы захватить провинцию, надо чтобы выполнялось одно из двух условий: либо она пограничная, либо граничит с какой-либо уже захваченной провинцией.

Чтобы сберечь силы своей армии, король Ректилании хочет установить блокаду столичной провинции, захватив как можно меньше провинций. Помогите ему выяснить, сколько провинций требуется захватить. Захватывать столичную провинцию нельзя, поскольку для этого сил армии Ректилании пока недостаточно.

Входные данные
В первой строке вводятся числа M и N (3 <= M, N <= 200). Следующие M строк содержат N символов каждая и задают карту Флатландии. Символ, находящийся в i + 1-й строке входных данных на j-м месте, представляет собой символ провинции, которой принадлежит квадратик (i, j). Все символы имеют ASCII-код больше 32 (пробела).

Выходные данные
Выведите единственное число - количество провинций, которые требуется захватить. Если установить блокаду невозможно, выведите "-1".

ID 54669. Электронные часы

Циферблат новых электронных часов, установленных на главном здании офиса фирмы Macrohard, состоит из 4 прямоугольных панелей, каждая из которых состоит из 6 рядов по 5 лампочек в каждом. Первые две панели отображают цифры, из которых складываются часы, а следующие две - минуты. (Если сейчас меньше 10 часов, первая панель отображает 0).

К сожалению, лампочки, установленные на панелях, были произведены компанией Sveta.Net, которая известна своим принципом , вследствие чего на следующий день люди, проходя мимо офиса компании, видели лишь некоторое подобие цифр, поскольку некоторые лампочки больше не горели.

Петя живет в доме, стоящем прямо напротив офиса компании Macrohard. В первый день после установки часов он зарисовал у себя в блокноте, как выглядят все цифры на панелях (панели однотипные, поэтому одна и та же цифра на различных панелях выглядит одинаково). Теперь Петя хочет узнать, можно ли по текущему изображению на часах однозначно определить, сколько сейчас времени. Помогите ему!

Входные данные
Входные данные содержат 6 строк по 20 символов в каждой - текущее изображение на часах. Первый прямоугольник задает первую панель, следующий - вторую, следующий - третью и последний - четвертую.

Выходные данные
Если можно точно определить время, которое сейчас отображается на часах, выведите это время в формате hh:mm. Если время нельзя определить однозначно, выведите AMBIGUITY. Если же в часах точно сломалось еще что-то, например, центральный процессор, который управляет лампочками, выведите ERROR.

ID 54948. Клетка для хомячка

Андрюше на день рождения подарили хомячка. Пока Андрюша не купил для него клетку, он решил сделать ему клетку из подручных средств. Для изготовления клетки он решил использовать набор кубиков, подаренный ему на прошлый день рождения. Однако, неожиданно выяснилось, что сестра Андрюши склеила кубики суперклеем, и отделить их друг от друга не представляется возможным.

Все кубики оказались склеены в две фигуры. Любые два кубика в каждой из фигур либо не имеют общих точек, либо имеют общую грань, либо имеют общее ребро, но в последнем случае есть кубик, с которым каждый из них имеет общую грань. Каждую фигуру можно положить на стол так, что каждый кубик будет касаться стола одной из своих граней.

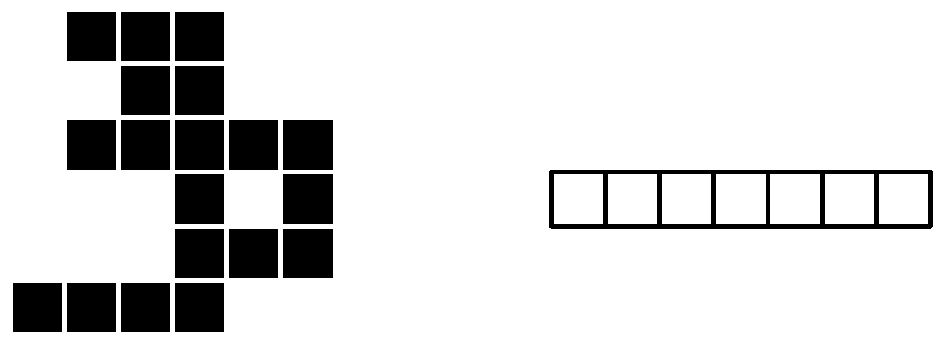
Теперь Андрюша хочет положить эти две фигуры на стол так, чтобы получилась клетка для хомячка. Фигуры должны быть положены таким образом, чтобы каждый кубик касался стола гранью. Стороны нижних граней кубиков должны быть параллельны сторонам стола. Любые два кубика, принадлежащие различным фигурам, должны либо не касаться друг друга, либо иметь общую грань, либо иметь общее ребро. Фигуры разрешается поворачивать и переворачивать.


Положив фигуры, Андрюша собирается выпустить хомячка на стол. Чтобы он не упал со стола, у него не должно быть возможности добраться от точки, в которую Андрюша его выпустит, до края стола. Хомячок не может перелезать через кубики, и, в частности, не может пролезть между двумя кубиками, имеющими общее ребро. Стол существенно больше каждой из фигур.

Андрюша хочет, чтобы площадь, по которой может бегать хомячок, была как можно больше. Помогите ему выяснить, какая максимальная площадь может быть у территории, до которой сможет добраться хомячок. Площадь грани кубика будем считать равной единице.

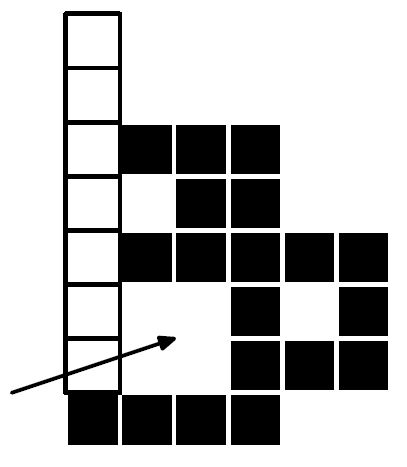
Например, две фигуры, показанные на рисунке выше, можно расположить как показано на следующем рисунке. Если выпустить хомячка в точку, отмеченную стрелкой, то доступная ему территория будет иметь площадь, равную четырем.

Входные данные
В первой строке вводятся два числа: h₁ и w₁ (1 <= h₁, w₁ <= 10). Следующие h₁
строк содержат по w₁ символов и описывают первую фигуру, вид сверху. Каждый из этих символов - либо "*" (звездочка), либо "." (точка), звездочка обозначает кубик, а точка – пустое место.

Далее в отдельной строке вводятся два числа: h₂ и w₂  (1 <= h₂,  w₂ <= 10). Следующие h₂ строк содержат по w₂ символов и описывают вторую фигуру в формате, аналогичном формату первой. Каждая из фигур связна и содержит хотя бы один кубик.

Выходные данные
Выведите одно число – максимальную площадь, которая может быть доступна хомячку. Если сделать клетку для хомячка невозможно, выведите 0.

ID 55072. Восстанови многоугольник

Вася нарисовал на клетчатой бумаге многоугольник, все стороны которого проходят по линиям сетки. После этого в каждой клетке он написал число, равное количеству сторон данной клетки, которые принадлежат сторонам многоугольника. Затем он стер многоугольник так, что остался листок бумаги, в каждой клетке которого написано число.

Восстановите нарисованный Васей многоугольник.

Входные данные
В первой строке входных данных содержатся два натуральных числа: Y - количество строк и X - количество столбцов листа (3 <= Y <= 1000, 3 <= X <= 1000). В каждой из следующих Y строк задается по X целых неотрицательных чисел, не превосходящих 4. Ни одна из сторон многоугольника не проходит по границе листа бумаги.

Выходные данные
Выведите искомый многоугольник в следующем формате.

Выходные данные должны содержать Y строк по 2X-1 символов в каждой (по одному символу на клетку и линию между клетками).

В первой строке выведите вертикальные отрезки в верхнем ряду клеток, обозначая их символом | (вертикальная черта - символ с кодом 124) и горизонтальные отрезки, отделяющие первый ряд клеток от следующего, обозначая их символом _ (подчеркивание). Если соответствующий отрезок в данном многоугольнике отсутствует, выведите вместо него символ . (точка). Во второй строке выведите в том же формате вертикальные отрезки во втором ряду и горизонтальные отрезки, отделяющие второй ряд от третьего. И т.д. В каждой строке на нечетных местах могут стоять только символы точка или подчеркивание, на четных местах - символы точка или вертикальная черта.

Гарантируется, что хотя бы одно решение существует. Если решений несколько, выведите любое из них.

ID 55100. Спираль

Вывести квадрат, состоящий из N*N клеток, заполненных числами от 1 до N² по спирали (см. примеры).

Входные данные
В первой строке находится единственное число N. 2 <= N <= 100.

Выходные данные
Выводится N строк по N чисел, разделённых пробелами. Не допускается начинать спираль в ином, кроме верхнего левого, углу, закручивать спираль против часовой стрелки или изнутри наружу.

ID 55105. Змейка

Вывести квадрат, состоящий из NxN ячеек, заполненных числами от 1 до N² "змейкой" (см. примеры).

Входные данные
В первой строке находится единственное число N. 2 <= N <= 100.

Выходные данные
Выводится N строк по N чисел, разделённых пробелами. Не допускаются начало змейки в другом углу или другое её направление.

ID 55136. Ближайшее число

Дана матрица A размером N*N, заполненная неотрицательными целыми числами. Расстояние между двумя элементами A_{i j} и A_{p q} определено как |i - p| + |j - q|.

Требуется заменить каждый нулевой элемент матрицы ближайшим ненулевым. Если есть две или больше ближайших ненулевых ячейки, нуль должен быть оставлен.

Ограничения: 1 <= N <= 200, 0 <= A_{i j} <= 1 000 000.

Входные данные
В первой строке содержится число N. Затем идут N строк по N чисел, разделённых пробелами и представляющих собой матрицу.

Выходные данные
Выводится N строк по N чисел, разделённых пробелами, - модифицированная матрица.

ID 55377. Крестики

Требуется расставить в некоторые клетки таблицы 3 x 3 крестики так, чтобы в каждой строке и в каждом столбце было заданное количество крестиков.

Входные данные
Вводятся 6 чисел (от 0 до 3) – требуемое количество крестиков в первом, втором, третьем столбце, в первой, второй, третьей строке.

Выходные данные
Требуется выдать количество возможных таблиц или 0, если таких таблиц нет.

ID 55389. Поворот

Дана картинка. Требуется повернуть ее на 90 градусов по часовой стрелке вокруг центра.

Картинка представляет собой квадрат, разбитый на N x N маленьких квадратиков. Каждый маленький квадратик закрашен в свой цвет. Цвета имеют номера от 0 до 255.

Входные данные
В первой строке вводится число одно натуральное число N, не превосходящее 100.

В следующих N строках записано по N чисел – цвета соответствующих квадратиков.

Выходные данные
Выведите N строк по N чисел, разделенных пробелами – цвета квадратиков после поворота картинки.

ID 27001. Крепкий дом

ID 55421. Экзамен

Даны две таблицы. В первой записана информация о школьниках (фамилия, имя и номер школы), а во второй – информация о результатах экзамена (фамилия, имя школьника и его оценка за экзамен). Требуется составить сводную таблицу, в которой будет указан номер школы и средняя оценка за экзамен всех учеников из этой школы (средняя оценка – это среднее арифметическое всех оценок, округленное до ближайшего сверху числа).

Входные данные
В первой строке вводится одно натуральное число N, не превосходящее 50 – количество школьников.

В следующих N строках вводится информация о школьниках в формате

Фамилия Имя Номер_Школы

Фамилия и имя не содержат пробелов, а номер школы – натуральное число, не превосходящее 2007.

В следующих N строках вводится информация об экзамене в формате

Фамилия Имя Оценка

Порядок учеников может быть иным, но имена и фамилии школьников такие же, как в предыдущем списке. Оценка – натуральное число от 2 до 5.

Гарантируется, что любые два школьника отличаются именем или фамилией.

Выходные данные
Вывести список, отсортированный по возрастанию номера школы, каждая строка которого имеет формат

Номер_Школы Средняя_Оценка

ID 55463. Преобрзование матрицы

Введем следующие операции надо прямоугольной таблицей символов. Пусть нам дана матрица А, состоящая из m строк (первый индекс) и n столбцов (второй индекс). Определим результирующую матрицу В для каждой из операций следующим образом:

• Транспозиция относительно главной диагонали (код операции '1'): B_j,i=A_i,j
• Транспозиция относительно другой диагонали (код операции '2'): B_n-j+1,m-i+1=A_i,j
• Горизонтальное отражение (код операции 'H'): B_m-i+1,_j=A_i,j
• Горизонтальное отражение (код операции 'V'): B_i,n-j+1=A_i,j
• Поворот на 90 ('A'), 180 ('B'), или 270 ('C') градусов по часовой стрелке: B_j,m-i+1=A_i,j (для 90º)
• Поворот на 90 ('X'), 180 ('Y'), или 270 ('Z') градусов против часовой стрелки: B_n-j+1,i=A_i,j (для 90º)

ID 55692. Шашки

Петя и Вася играли в шашки по описанным ниже правилам. В какой-то момент забежавший в комнату кот перевернул доску, на которой играли Петя и Вася. К счастью, у них осталась запись сделанных ходов, используя которую можно восстановить расположение шашек к моменту, когда забежал кот.

Напишите программу, которая выведет положение шашек на доске после выполнения описанных ходов.

Правила игры

Игра происходит на стандартной доске (8х8), которая располагается так, что у игрока, играющего белыми, левая нижняя клетка является черной, и с нее начинается нумерация как строк, так и столбцов. Строки доски нумеруются числами от 1 до 8, столбцы — латинскими буквами от a до h.
 

ID 55697. Сапер

Мальчику Васе очень нравится известная игра "Сапер" ("Minesweeper").

В "Сапер" играет один человек. Игра идет на клетчатом поле (далее будем называть его картой) NxM (N строк, M столбцов). В K клетках поля стоят мины, в остальных клетках записано либо число от 1 до 8 — количество мин в соседних клетках, либо ничего не написано, если в соседних клетках мин нет. Клетки являются соседними, если они имеют хотя бы одну общую точку, в одной клетке не может стоять более одной мины. Изначально все клетки поля закрыты. Игрок за один ход может открыть какую-нибудь клетку. Если в открытой им клетке оказывается мина — он проигрывает, иначе игроку показывается число, которое стоит в этой клетке, и игра продолжается. Цель игры — открыть все клетки, в которых нет мин.

У Васи на компьютере есть эта игра, но ему кажется, что все карты, которые в ней есть, некрасивые и неинтересные. Поэтому он решил нарисовать свои. Однако фантазия у него богатая, а времени мало, и он хочет успеть нарисовать как можно больше карт. Поэтому он просто выбирает N, M и K и расставляет мины на поле, после чего все остальные клетки могут быть однозначно определены. Однако на определение остальных клеток он не хочет тратить свое драгоценное время. Помогите ему!

По заданным N, M, K и координатам мин восстановите полную карту.

Входные данные
В первой строке входного файла содержатся числа N, M и K (1≤N≤200, 1≤M≤200, 0≤K≤N≤M). Далее идут K строк, в каждой из которых содержится по два числа, задающих координаты мин. Первое число в каждой строке задает номер строки клетки, где находится мина, второе число — номер столбца. Левая верхняя клетка поля имеет координаты (1,1), правая нижняя — координаты (N,M).

Выходные данные
Выходной файл должен содержать N строк по M символов — соответствующие строки карты. j-й символ i-й строки должен содержать символ ‘*‘ (звездочка) если в клетке (i,j) стоит мина, цифру от 1 до 8, если в этой клетке стоит соответствующее число, либо ‘.‘ (точка), если клетка (i,j) пустая.

ID 55698. Робот K-79

Петя написал программу движения робота К-79. Программа состоит из следующих команд:

• S — сделать шаг вперед
• L — повернуться на 90º влево
• R — повернуться на 90º вправо

ID 56882. Квадрат

Требуется в каждую клетку квадратной таблицы размером NxN поставить ноль или единицу так, чтобы в любом квадрате размера KxK было ровно S единиц.

Входные данные
Во входных данных записаны три числа — N, K, S (1 ≤ N ≤ 100, 1 ≤ K ≤ N, 0 ≤ S ≤ K²).

Выходные данные
Выведите заполненную таблицу. Числа в строке должны разделяться пробелом, каждая строка таблицы должна быть выведена на отдельной строке файла. Если решений несколько, выведите любое из них.