| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Дата и время
Обход в глубину
Коля очень мечтал поступить в лучший ВУЗ – МГТУ им. Н.Э. Баумана и у него это получилось. Однако, ему не хватило 1 балла для того, чтобы ему предоставили общежитие, потому ему придётся добираться до института на электричках, благо институт находится не только у метро, но и у станции электричек, от которой идти всего 20 минут пешком.
Коля очень пунктуальный мальчик, потому, он каждый раз вечером садится и выписывает расписание электричек на следующий день, чтобы понять, как ему лучше всего добраться до института, чтобы успеть к нужной паре. Но есть проблема, Коле приходится добираться на нескольких электричках, так как он живёт уж очень далеко.
Коля хоть и пунктуальный мальчик, но он, как и все, очень любит поспать, поэтому он решил рассчитать во сколько он доберётся до института в самом оптимистичном случае.
Стоит учесть тот момент, что иногда электрички сбиваются с расписания и могут прийти раньше до 10 минут (включительно), но время в пути у них неизменно.
Помогите Коле рассчитать, во сколько ему нужно встать, по самому оптимистическому сценарию, чтобы приехать к паре вовремя, если известно время начала пары и расписание электричек на каждой станции, с которой он будет отправляться.
Входные данные
На первой строке задаётся время начала пары, к которой Коля должен успеть в формате (hh:mm).
На второй строке задаётся количество станций, с которых будет отправляться Коля (1 <= N <= 10).
На третьей строке задаётся N целых чисел через пробел (1 <= M_1, M_2, …, M_n <= 20) – количество отправлений поездов для каждой станции.
Далее следует N блоков данных по M строк в каждой из которых задано время отправления электрички со станции по расписанию и время в пути до нужной Коле станции (через точку с запятой) (например, 12:10;30, что означает, что электричка отправляется в 12:10, в пути она 30 минут.
Выходные данные
Вывести на одной строке время в формате hh:mm (например, 08:10 или 12:13), в которое Коля должен быть уже на первой станции электричек, чтобы отправиться в институт, притом в самом оптимистичном варианте.
Примечание:
•на вход подаются расписания электричек со станций в порядке,в котором Коля должен на них прибывать;
•гарантируется, что Коля 100% может успеть на пару вовремя.
| |
![]()
|
1/
1
|
|
Темы:
Деревья
Жадный алгоритм
Конструктив
Обход в глубину
На производстве расположены \(n\) роботов, пронумерованных от \(1\) до \(n\). Любая пара роботов может быть либо соединена проводом, либо нет. Известно, что \(i\)-й робот соединен с \(k_i\) другими роботами с номерами \(v_{i,1}, \ldots, v_{i,k_i}\). Провода двухсторонние, то есть если \(i\) связан с \(j\), то \(j\) связан с \(i\) (иными словами, \((i, j)\) и \((j, i)\) — это один и тот же провод).
Вы находитесь рядом с роботом номер \(n\). Роботом номер \(t\) можно управлять, если он связан с \(n\)-м некоторой цепочкой проводов, то есть
-
либо если \(t = n\);
-
либо если существуют такие \(i_1, \ldots, i_k\), что \(i_1 = n\), \(i_k = t\), и любые два соседних в этой последовательности робота \(i_j\) и \(i_{j + 1}\) связаны проводом.
Любому из роботов, которыми можно управлять, можно послать команду <<извлеки второй конец подключенного к себе провода и подключи его к другому роботу>>. Иными словами, если роботом номер \(t\) можно управлять, и есть провод, соединяющий его с роботом номер \(x\), то можно заменить провод \((t, x)\) на провод \((t, y)\) для любого \(y \neq t\), еще не связанного проводом с \(t\). Обратите внимание, что после этого вы можете потерять управление над \(t\)-м роботом, если единственная связь \(t\)-го с \(n\)-м проходила через \(x\)-й.
Ваша задача — получить управление над максимально возможным количеством роботов на производстве. Найдите это количество и самую короткую последовательность действий, приводящую к такому исходу.
Формат входных данных
В первой строке записано целое число \(T\) (\(1 \le T \le 1000\)) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит одно целое число \(n\) (\(1 \leq n \leq 10^5\)) — количество роботов.
Затем следуют \(n\) строк, в \(i\)-й из которых записаны числа \(k_i\) (\(0 \le k_i \le n - 1\)) и \(v_{i,1}, \ldots, v_{i,k_i}\) (\(1 \le v_{i,j} \le n\); \(v_{i,j} \neq i\)) — количество проводов, подключенных к \(i\)-му роботу, и номера роботов на противоположных концах этих проводов. Гарантируется, что данные корректны: никакие два провода не соединяют одну и ту же пару роботов, и если \(j \in v_i\), то \(i \in v_j\).
Также гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^5\) и сумма количества проводов по всем наборам входных данных не превосходит \(1.5 \cdot 10^5\).
Формат выходных данных
Для каждого набора входных данных выведите в первой строке через пробел максимальное количество роботов, управление над которыми можно получить, и количество действий \(k\), которое для этого понадобится.
В следующих \(k\) строках выведите сами описания действий в формате <<\(y\) + \(t\) - \(x\)>> (\(1 \leq t, x, y \leq n\); \(x \neq y\)). Каждая такая строка соответствует замене провода \((t, x)\) на провод \((t, y)\).
Если возможных ответов несколько, выведите любой. Обратите внимание, что \(k\) при этом обязано быть наименьшим, при котором можно подключить максимальное количество роботов.
| |
![]()
|
1/
1
|
|
Темы:
Обход в глубину
Жадный алгоритм
Конструктив
Деревья
На производстве расположены \(n\) роботов, пронумерованных от \(1\) до \(n\). Любая пара роботов может быть либо соединена проводом, либо нет. Всего на производстве \(m\) проводов и \(i\)-й из них сейчас соединяет роботов с номерами \(a_i\) и \(b_i\).
Вы находитесь рядом с роботом номер \(1\). Роботом номер \(t\) можно управлять, если он связан с первым некоторой цепочкой проводов, то есть
-
либо если \(t = 1\);
-
либо если существуют такие \(i_1, \ldots, i_k\), что \(i_1 = 1\), \(i_k = t\), и любые два соседних в этой последовательности робота \(i_j\) и \(i_{j + 1}\) связаны проводом.
Любому из роботов, которыми можно управлять, можно послать команду <<извлеки второй конец подключенного к себе провода и подключи его к другому роботу>>. Иными словами, если роботом номер \(t\) можно управлять, и есть провод, соединяющий его с роботом номер \(x\), то можно заменить провод \((t, x)\) на провод \((t, y)\) для любого \(y \neq t\), еще не связанного проводом с \(t\). Обратите внимание, что после этого вы можете потерять управление над \(t\)-м роботом, если единственная связь \(t\)-го с первым проходила через \(x\)-й.
Ваша задача — получить управление над максимально возможным количеством роботов на производстве. Найдите это количество и самую короткую последовательность действий, приводящую к такому исходу.
Формат входных данных
В первой строке записано целое число \(T\) (\(1 \le T \le 1000\)) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит целые числа \(n\) и \(m\) (\(1 \leq n \leq 10^5\); \(0 \leq m \leq 1.5 \cdot 10^5\)) — количество роботов и количество проводов, соответственно.
В следующих \(m\) строках дано описание проводов: в \(i\)-й строке даны целые числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n\); \(a_i \neq b_i\)) — номера роботов, соединенных \(i\)-м проводом. Гарантируется, что никакие два провода не соединяют одну и ту же пару роботов.
Также гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^5\) и сумма \(m\) по всем наборам входных данных не превосходит \(1.5 \cdot 10^5\).
Формат выходных данных
Для каждого набора входных данных выведите в первой строке через пробел максимальное количество роботов, управление над которыми можно получить, и количество действий \(k\), которое для этого понадобится.
В следующих \(k\) строках выведите сами описания действий по одному на каждой строке. Описание действия должно состоять из трех целых чисел \(t\), \(x\) и \(y\) (\(1 \leq t, x, y \leq n\); \(x \neq y\)), означающих, что робот номер \(t\) меняет провод \((t, x)\) на провод \((t, y)\).
Если возможных ответов несколько, выведите любой. Обратите внимание, что \(k\) при этом обязано быть наименьшим, при котором можно подключить максимальное количество роботов.
| |
![]()
|
2/
1
|
|
Темы:
Обход в глубину
Алгоритм Флойда
Дан ориентированный граф. Используя алгоритм Флойда определите, есть ли в заданном графе цикл.
Формат входных данных
В первой строке вводится число вершин N≤ 50. Далее в N строках следуют по N чисел, каждое из которых – 0 или 1. j-ое число в i-ой строке равно 1 тогда и только тогда, когда существует ребро, идущее из i-ой вершины в j-ую. Гарантируется, что на диагонали матрицы будут стоять нули.
Формат выходных данных
Выведите 0, если в заданном графе цикла нет, и 1, если он есть.
| |
![]()
|
144/
97
|
|
Темы:
Способы задания графа
Обход в глубину
У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.
Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.
Входные данные
В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.
Выходные данные
Выведите единственное число: минимальное количество копилок, которые необходимо разбить.
Примечание
Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.
Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
| |
![]()
|
1/
1
|
|
Темы:
Обход в ширину
Обход в глубину
Карту местности условно разбили на квадраты, и посчитали среднюю высоту над уровнем моря для каждого квадрата.
Когда идет дождь, вода равномерно выпадает на все квадраты. Если один из четырех соседних с данным квадратом квадратов имеет меньшую высоту над уровнем моря, то вода с текущего квадрата стекает туда (и, если есть возможность, то дальше), если же все соседние квадраты имеют большую высоту, то вода скапливается в этом квадрате.
Разрешается в некоторых квадратах построить водостоки. Когда на каком-то квадрате строят водосток, то вся вода, которая раньше скапливалась в этом квадрате, будет утекать в водосток.
Если есть группа квадратов, имеющих одинаковую высоту и образующих связную область, то если хотя бы рядом с одним из этих квадратов есть квадрат, имеющий меньшую высоту, то вся вода утекает туда, если же такого квадрата нет, то вода стоит во всех этих квадратах. При этом достаточно построить водосток в любом из этих квадратов, и вся вода с них будет утекать в этот водосток.
Требуется определить, какое минимальное количество водостоков нужно построить, чтобы после дождя вся вода утекала в водостоки.
Входные данные
Во входном файле записаны сначала числа N и M, задающие размеры карты — натуральные числа, не превышающие 100. Далее идет N строк, по M чисел в каждой, задающих высоту квадратов карты над уровнем моря. Высота задается натуральным числом, не превышающим 10000. Считается, что квадраты, расположенные за пределами карты, имеют высоту 10001 (то есть вода никогда не утекает за пределы карты).
Выходные данные
В выходной файл выведите минимальное количество водостоков, которое необходимо построить.
| |
![]()
|
1/
1
|
|
Темы:
Обход в глубину
Элементарная геометрия
В саду Бена расположено n ульев. Некоторые из них соединены друг с другом или с домом Бена прямыми дорожками. Бен гуляет только по дорожкам, переходя с одной на другую только возле очередного улья. Ни дом Бена, ни какой-либо улей не расположены на дорожке, соединяющей другие два улья. Дорожки организованы таким образом, что Бен может дойти от дома до любого улья только единственным способом.
Каждую неделю Бен делает обход ульев. Он начинает от своего дома и идет по дорожкам, посещая каждый улей по крайней мере один раз, минимизируя при этом общий путь. Сын Бена решил помочь своему стареющему отцу и проложить еще одну прямую дорожку между двумя ульями, так чтобы путь Бена от дома через все ульи с возвращением к дому стал как можно короче. Она, как и старые дорожки, проходить мимо дома или другого улья не должна.
Входные данные
На вход сначала подается число n — количество ульев (1≤n≤200).
Введем координаты так, что дом Бена будет располагаться в точке (0, 0). В следующих n строках входных данных записаны координаты ульев в саду Бена. Они не превосходят 10000 по абсолютному значению. Никакие два улья не совпадают, и нет ульев, расположенных в точке (0, 0). Будем считать, что они пронумерованы от 1 до n.
Следующие n строк описывают дорожки — каждая дорожка описывается номерами объектов, которые она соединяет. Дом Бена имеет номер 0.
Выходные данные
Выведите два числа — номера объектов, которые надо соединить дополнительной дорожкой. Если требуемой прямой дорожки, сокращающей общий путь Бена не существует, то выведите –1.
| |
![]()
|
1/
1
|
|
Темы:
Обход в глубину
В операционной системе Xunil информация обо всех файлах и директориях хранится в специальном файле в следующем формате:
emoh
vonavi
a.doc
b.doc
vortep
.bashrc
vorodis
onrop
1.avi
2.avi
rav
bil
Имена файлов, и только они, содержат точку.
Требуется по данному имени файла найти путь к нему. Если таких файлов несколько, вывести путь к файлу, который записан выше.
Входные данные
В первой строке вводится имя искомого файла. Во второй строке вводится общее количество файлов и директорий. В остальных строках вводится информация о файлах и директориях в указанном выше формате (директория или файл, находящиеся внутри другой директории, отделяются одним дополнительным пробелом в начале строки). Количество строк в файле и количество символов в каждой строке не превосходит 100.
Выходные данные
Выведите путь к файлу в формате /директория/директория/…/файл
Гарантируется, что такой файл есть.
Гарантируется, что длина строки ответа не превосходит 255.
| |
![]()
|
1/
1
|
|
Темы:
Способы задания графа
Обход в ширину
Обход в глубину
Прямоугольную таблицу, состоящую из N строк и M столбцов, раскрашивают следующим образом. Каждый столбец таблицы и каждую строку красят либо в синий, либо в желтый цвет. В итоге клетки, оказавшиеся на пересечении синего столбца и синей строки оказываются синими, желтого столбца и желтой строки — желтыми, а клетки на пересечении синего столбца и желтой строки, или, наоборот, желтого столбца и синей строки — зелеными.
Раскраска всех клеток таблицы (или просто сама таблица) называется правильной, если она может быть получена описанным выше способом.
Вам дана прямоугольная таблица, которую нужно раскрасить таким образом. Про некоторые клетки известно, какого цвета они должны быть, а остальные клетки могут в итоге быть любого цвета. Определите, сколько существует различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет.
Входные данные
Вводятся числа N и M — количество строк и столбцов таблицы (1≤N≤30, 1≤M≤30). Далее записано N строк по M чисел в каждой, задающие цвета, в которые должны быть окрашены клетки:
0 — клетка может в итоге быть любого цвета
1 — клетка должна быть синей
2 — клетка должна быть желтой
3 — клетка должна быть зеленой
Выходные данные
Выведите одно число — количество различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет. Обратите внимание, что если два или более способов раскраски столбцов и строк таблицы приводят к одинаковой раскраске самой таблицы, то это нужно считать как один вариант раскраски таблицы (см. пример 2).
| |
![]()
|
1/
1
|
|
Темы:
Способы задания графа
Обход в глубину
У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.
Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.
Входные данные
В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.
Выходные данные
Выведите единственное число: минимальное количество копилок, которые необходимо разбить.
Примечание
Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.
Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
| |
![]()
|
1/
1
|
|
Темы:
Остатки
Обход в глубину
Рассмотрим таблицу, состоящую из N строк и M столбцов. Если в каждой ячейке такой таблицы стоит целое число, назовем такую таблицу целочисленной матрицей. Скажем, что эта матрица кратна чиcлу p, если все числа в ее ячейках кратны p.
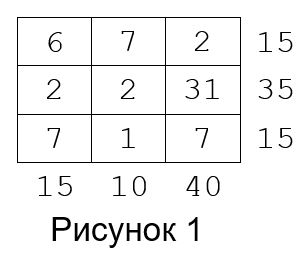
Рассмотрим теперь суммы элементов матрицы по строкам и столбцам соответственно. Обозначим сумму чисел i-й строки за Hi, а сумму чисел j-го столбца за Vj. Упорядоченный набор чисел (H1, H2, …, HN, V1, V2, …, VM) назовем профилем матрицы. Скажем, что матрица почти кратна p, если все числа, входящие в ее профиль, кратны p. Почти кратная 5 матрица и ее профиль изображены на рисунке 1.
Если две матрицы A и B имеют одинаковый размер, причем элемент, стоящий на пересечении i-й строки и j
-го столбца в матрице A отличается от соответствующего элемента матрицы B не более чем на p, скажем, что A отличается от B не более чем на p. Скажем, что матрица B похожа на матрицу A относительно числа p, если
1. отличается от не более чем на p
2. профили B и A совпадают.
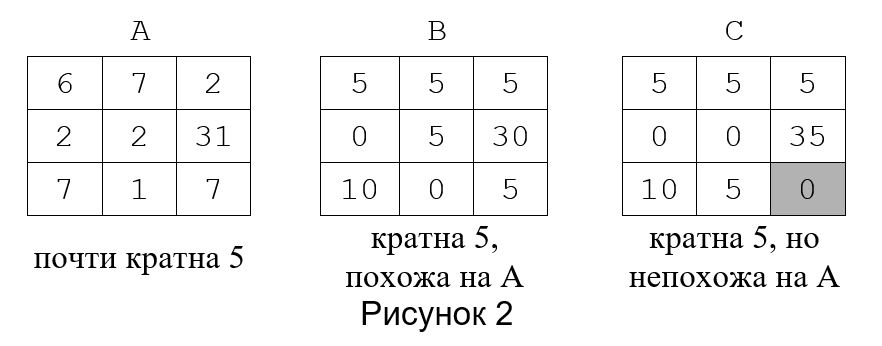
На рисунке 2 изображены две похожие относительно числа 5 матрицы, первая из них почти кратна 5, а вторая кратна 5. Третья матрица на рисунке 2 тоже кратна 5, но непохожа на первую (хотя похожа на вторую).
Дано число p и почти кратная p матрица A. Ваша задача - найти такую матрицу B, чтобы она была кратна p и похожа на A относительно p.
Входные данные
В первой строке входных данных задаются целые числа p (1 <= p <= 10), N и M (1 <= N, M <= 30). Следующие N строк содержат по M целых неотрицательных чисел, не превышающих 1000, которые являются элементами исходной матрицы A.
Выходные данные
Выведите матрицу B по строкам - сначала M элементов первой строки, затем M элементов второй, и т. д. Разделяйте числа пробелами и/или переводами строк. Заботиться о красивом форматировании таблицы не надо. Если искомой матрицы не существует, выведите единственное число - "-1". Если решений несколько, выведите любое из них.
| |
![]()
|
2/
2
|
|
Темы:
Способы задания графа
Обход в глубину
Дима обнаружил у папы на столе специальный чертежный прибор, похожий на циркуль - измеритель. Измеритель отличается от обычного циркуля тем, что в обеих его ножках находятся иголки (у обычного циркуля в одной ножке находится иголка, а в другой - грифель).
Дима взял клетчатый лист бумаги, установил между иглами измерителя некоторое расстояние, прочно зафиксировав его, и начал втыкать измеритель в лист бумаги. Каждый раз Дима втыкал в лист обе иглы измерителя, при этом он всегда делал это так, что дырочки получались в точках пересечениях линий, которыми лист разлинован на клетки. При этом в одну и ту же дырку Дима мог вставлять измеритель несколько раз.
Вечером папа нашел лист, с которым развлекался Дима, и решил выяснить, какое расстояние между иглами измерителя Дима мог установить. Все, что знает папа - координаты дырок, проделанных иглами измерителя. Помогите Папе решить поставленную задачу.
Входные данные
В первой строке вводится число n
- количество дырок (2 <= n <= 1000). Следующие n строк содержат по два целых числа - координаты дырок. Координаты не превышают 104
по абсолютной величине.
Выходные данные
В первой строке выведите k
- количество различных расстояний, которые Дима мог установить между иглами измерителя. Следующие k строк должны содержать искомые расстояния, по одному вещественному числу в строке. Расстояния должны быть выведены в возрастающем порядке. Каждое число должно быть выведено с точностью не менее, чем 10-9.
Гарантируется, что существует по крайней мере одно расстояние, которое Дима мог установить между иглами измерителя.
| |
![]()
|
2/
2
|
|
Темы:
Двумерные массивы
Обход в глубину
Простые задачи на перебор
Андрюше на день рождения подарили хомячка. Пока Андрюша не купил для него клетку, он решил сделать ему клетку из подручных средств. Для изготовления клетки он решил использовать набор кубиков, подаренный ему на прошлый день рождения. Однако, неожиданно выяснилось, что сестра Андрюши склеила кубики суперклеем, и отделить их друг от друга не представляется возможным.
Все кубики оказались склеены в две фигуры. Любые два кубика в каждой из фигур либо не имеют общих точек, либо имеют общую грань, либо имеют общее ребро, но в последнем случае есть кубик, с которым каждый из них имеет общую грань. Каждую фигуру можно положить на стол так, что каждый кубик будет касаться стола одной из своих граней.
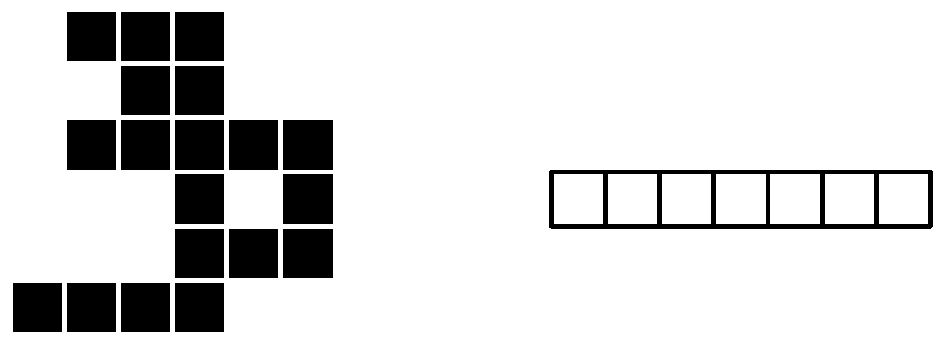
Теперь Андрюша хочет положить эти две фигуры на стол так, чтобы получилась клетка для хомячка. Фигуры должны быть положены таким образом, чтобы каждый кубик касался стола гранью. Стороны нижних граней кубиков должны быть параллельны сторонам стола. Любые два кубика, принадлежащие различным фигурам, должны либо не касаться друг друга, либо иметь общую грань, либо иметь общее ребро. Фигуры разрешается поворачивать и переворачивать.
Положив фигуры, Андрюша собирается выпустить хомячка на стол. Чтобы он не упал со стола, у него не должно быть возможности добраться от точки, в которую Андрюша его выпустит, до края стола. Хомячок не может перелезать через кубики, и, в частности, не может пролезть между двумя кубиками, имеющими общее ребро. Стол существенно больше каждой из фигур.
Андрюша хочет, чтобы площадь, по которой может бегать хомячок, была как можно больше. Помогите ему выяснить, какая максимальная площадь может быть у территории, до которой сможет добраться хомячок. Площадь грани кубика будем считать равной единице.
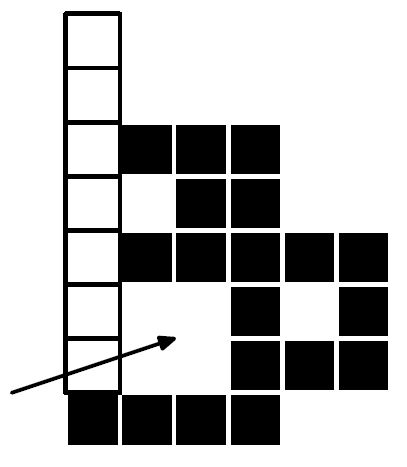
Например, две фигуры, показанные на рисунке выше, можно расположить как показано на следующем рисунке. Если выпустить хомячка в точку, отмеченную стрелкой, то доступная ему территория будет иметь площадь, равную четырем.
Входные данные
В первой строке вводятся два числа: h1 и w1 (1 <= h1, w1 <= 10). Следующие h1
строк содержат по w1 символов и описывают первую фигуру, вид сверху. Каждый из этих символов - либо "*" (звездочка), либо "." (точка), звездочка обозначает кубик, а точка – пустое место.
Далее в отдельной строке вводятся два числа: h2 и w2 (1 <= h2, w2 <= 10). Следующие h2 строк содержат по w2 символов и описывают вторую фигуру в формате, аналогичном формату первой. Каждая из фигур связна и содержит хотя бы один кубик.
Выходные данные
Выведите одно число – максимальную площадь, которая может быть доступна хомячку. Если сделать клетку для хомячка невозможно, выведите 0.
| |
![]()
|
1/
1
|
|
Темы:
Способы задания графа
Обход в глубину
У Пети в саду растет яблоня. Воодушевленный историей об Исааке Ньютоне, который, как известно, открыл закон всемирного тяготения после того, как ему на голову упало яблоко, Петя с целью повысить свою успеваемость по физике часто сидит под яблоней.
Однако, поскольку по физике у Пети твердая тройка, яблоки с его яблони падают следующим образом. В какой-то момент одно из яблок отрывается от ветки, на которой оно висит, и начинает падать строго вниз. Если в некоторый момент оно задевает другое яблоко, то то тоже отрывается от своей ветки и начинает падать вниз, при этом первое яблоко не меняет направление своего падения. Вообще, если любое падающее яблоко заденет другое яблоко на своем пути, то оно также начнет падать.
Таким образом, в любой момент каждое яблоко либо висит на ветке, либо падает строго вниз, причем все яблоки кроме первого, чтобы начать падать, должны сначала соприкоснуться с каким-либо другим падающим яблоком.
Выясните, какие яблоки упадут с Петиной яблони.
Входные данные
В первой строке вводится число N - количество яблок на Петиной яблоне (1 <= N <= 200). Следующие N строк содержат описания яблок. Будем считать все яблоки шарами. Каждое яблоко задается координатами своей самой верхней точки (той, где оно исходно прикреплено к дереву, длиной черенка пренебрежем) xi, yi и zi и радиусом ri ( -10000 <= xi, yi, zi <= 10000, 1 <= ri <= 10000, все числа целые). Гарантируется, что изначально никакие яблоки не пересекаются (даже не соприкасаются). Ось OZ направлена вверх.
Выходные данные
В первой строке выведите количество яблок, которые упадут с яблони, если начнет падать первое яблоко. В следующей строке выводите номера упавших яблок. Яблоки нумеруются, начиная с 1, в том порядке, в котором они заданы во входных данных.
| |
![]()
|
1/
1
|
|
Темы:
Обход в глубину
Двумерные массивы
Государство Флатландия представляет собой прямоугольник размером M × N, состоящий из единичных квадратиков. Флатландия разделена на K провинций (2 <= K <= 100). Каждая провинция представляет собой связное множество квадратиков, т.е. из каждой точки провинции можно дойти до любой другой ее точки, при этом разрешается переходить с квадратика на квадратик, только если они имеют общую сторону (общей вершины недостаточно). Во Флатландии нет точки, которая граничила бы более чем с тремя провинциями (т.е. четыре квадратика, имеющие общую вершину, не могут принадлежать четырем разным провинциям).
Каждая провинция имеет свой символ. Столица Флатландии находится в провинции, которой принадлежит символ A (заглавная латинская буква A). Провинция называется пограничной, если она содержит граничные квадратики. Провинция, в которой находится столица Флатландии, не является пограничной.
Король соседнего с Флатландией королевства Ректилания решил завоевать Флатландию. Для этого он хочет захватить столицу Флатландии. Однако он знает, что сил его армии недостаточно, чтобы сделать это сразу. Поэтому сначала он хочет окружить столичную провинцию, чтобы ослабить силы противника долгой блокадой, а потом захватить столицу.
Чтобы окружить провинцию, требуется захватить все провинции, с которыми она граничит. Две провинции граничат, если существует два квадратика, имеющие общую сторону, один из которых принадлежит первой из них, а другой - второй. Чтобы захватить провинцию, надо чтобы выполнялось одно из двух условий: либо она пограничная, либо граничит с какой-либо уже захваченной провинцией.
Чтобы сберечь силы своей армии, король Ректилании хочет установить блокаду столичной провинции, захватив как можно меньше провинций. Помогите ему выяснить, сколько провинций требуется захватить. Захватывать столичную провинцию нельзя, поскольку для этого сил армии Ректилании пока недостаточно.
Входные данные
В первой строке вводятся числа M и N (3 <= M, N <= 200). Следующие M строк содержат N символов каждая и задают карту Флатландии. Символ, находящийся в i + 1-й строке входных данных на j-м месте, представляет собой символ провинции, которой принадлежит квадратик (i, j). Все символы имеют ASCII-код больше 32 (пробела).
Выходные данные
Выведите единственное число - количество провинций, которые требуется захватить. Если установить блокаду невозможно, выведите "-1".
| |
![]()
|
1/
1
|
|
Темы:
Бинарный поиск по ответу
Обход в глубину
В столице одной Очень Демократической Страны все жители в 8 часов утра одновременно выходят со станций метро, ближайших к месту своей работы, и дальше добираются до работы на автобусах. Мэр города хочет построить еще одну станцию метро так, чтобы после этого время, к которому все люди доберутся до места своей работы (то есть время, когда последний работник окажется на работе), было наименьшим возможным.
Автобусное сообщение в столице устроено следующим образом. Есть N автобусных остановок, в частности, возле каждой станции метро расположено по остановке. Между N – 1 парой остановок постоянно курсируют автобусы, время движения от одной остановки до другой – 1 минута. Временем ожидания и пересадки можно пренебречь. Автобусное сообщение в столице организовано так, что от любой автобусной остановки до любой другой можно добраться на автобусах (возможно, с пересадками).
Входные данные
В первой строке входных данных содержатся два числа N и M – количество автобусных остановок и станций метро соответственно (2 ≤ N ≤ 50 000, 1 ≤ M ≤ 1 000, M < N).
Во второй строке задаются через пробел M чисел – номера автобусных остановок, рядом с которыми есть станции метро (каждая – не более одного раза).
В следующих N – 1 строках записано по два числа – номера автобусных остановок, между которыми курсирует автобус. (Автобус ходит в обоих направлениях. Каждый маршрут указан один раз.)
Выходные данные
Выведите два числа – сначала наибольшее время за которое кто-то будет и после строительства добираться на работу, а затем номер автобусной остановки, рядом с которой следует построить новую станцию метро. (Строить можно возле тех автобусных остановок, возле которых еще нет станций метро). Если решений несколько, выведите одно из них.
| |
![]()
|
23/
1
|
|
Темы:
Обход в глубину
Сканирующая прямая
Элементарная геометрия
В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.
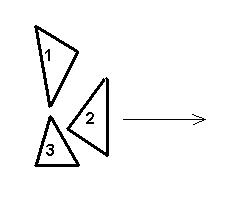
Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.
Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).
Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).
Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).
Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.
Входные данные
В первой строке вводится натуральное число N( 1 ≤ N ≤ 30 000).
В каждой из следующих N строк содержится по 6 чисел: x1, y1, x2, y2, x3, y3 – координаты трех вершин скутера на старте, целые числа, не превосходящие по модулю 106. В начальный момент скутеры не задевают друг друга.
Выходные данные
Выведите через пробел N чисел – номера скутеров в том порядке, в котором они могут стартовать. Если решений несколько, выведите одно любое из них. Если решений нет, выведите одно число -1.
Примечание
Первый тест соответствует приведенному рисунку. Ответ 2 3 1 в этом тесте также является правильным
| |
![]()
|
1/
1
|
|
Темы:
Обход в глубину
В Тридесятом государстве есть N фирм, занимающихся разработкой программного обеспечения. Однажды известный олигарх Тридесятого государства Иванушка решил монополизировать эту отрасль. Для этого он хочет купить максимальное число программистских фирм Тридесятого государства.
Он разослал предложения всем N компаниям и через некоторое время получил от каждой их них согласие или отказ. Однако он знает, что в бизнесе очень многое зависит от взаимного доверия партнеров.
В результате небольшого исследования Иванушка установил, между какими компаниями существует взаимное доверие (причем всегда если компания доверяет компании B, то компания B доверяет компании A).
Теперь, при желании, Иванушка может повторно разослать предложения всем компаниям, включив в письма список компаний, давших согласие участвовать в его проекте. При этом каждая компания, независимо от своего первоначального мнения дает согласие, если в списке есть хотя бы одна компания, которой она доверяет, и отказ в противном случае. Таким образом, некоторые компании, которые изначально не согласились участвовать в проекте, могут теперь дать свое согласие, а некоторые из давших согласие — наоборот отказаться. В результате этого у Иванушки формируется новый список, который он опять может разослать фирмам. Он может сколь угодно долго повторять операцию, каждый раз рассылая текущий список. Иванушка может остановить процесс в любой момент и заключить договора с теми, кто после последней рассылки дал согласие.
Напишите программу, которая определит, какое максимальное число компаний может объединить Иванушка под своим началом.
Будем считать, что Иванушка — честный предприниматель и он никогда не подтасовывает рассылаемые им списки.
Входные данные
В первой строке входных данных содержится число N — количество фирм (1≤N≤2000). Далее идут N чисел, описывающих ответ фирмы на первое предложение Иванушки (1 — согласие, 0 — отказ). Далее задается число M (0≤M≤200000) — количество пар компаний, между которыми существует доверие. Далее следуют M пар чисел, задающих номера фирм, между которыми существует взаимное доверие (числа в паре не могут быть одинаковыми). Любая пара компаний упоминается в этом списке не более одного раза.
Выходные данные
Выведите одно число — максимальное число фирм, которое сможет купить Иванушка.
| |
![]()
|
2/
2
|
|
Темы:
Способы задания графа
Обход в глубину
На пригородной железной дороге N станций и M соединяющих их перегонов. Любые две станции соединены не более чем одним перегоном. Сеть перегонов устроена так, что, отправившись от любой станции, можно вернуться на нее, только проехав хотя бы один перегон дважды. На железной дороге организовано движение электричек. Каждая электричка ходит в обоих направлениях по своему маршруту между двумя конечными станциями и останавливается на всех промежуточных станциях
Для удобства пассажиров руководство железной дороги решило ввести новую систему оплаты проезда. По этой системе каждой станции присваивается некоторое целое число, называемое тарифным номером этой станции. Стоимость проезда между двумя станциями без пересадок определяется модулем разности тарифных номеров этих станций. Тарифные номера станций вдоль маршрута каждой электрички должны изменяться монотонно, то есть при движении в каком-либо направлении строго возрастать и, следовательно, строго убывать при движении в обратном направлении. Это обеспечивает рост стоимости проезда с увеличением количества пройденных перегонов.
Требуется написать программу, которая назначит каждой станции тарифный номер.
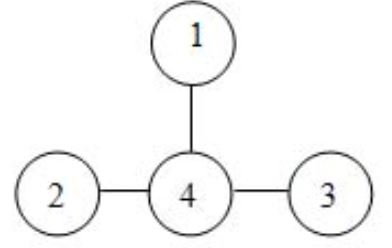 |
4 станции, 3 перегона: 1-4, 2-4, 3-4
Маршруты: 1-4-2, 2-4-3, 3-4-1.
Ответ: решения нет
|
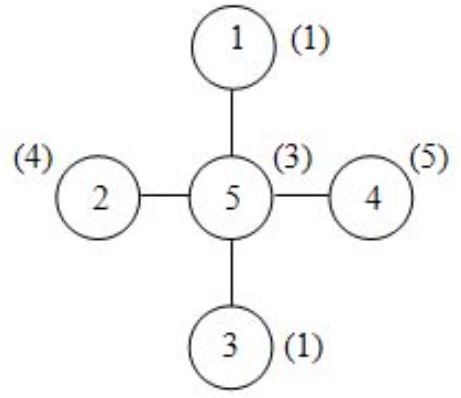 |
5 станций, 4 перегона: 1-5, 2-5, 3-5, 4-5
Маршруты: 1-5-2, 2-5-3, 3-5-4, 4-5-1.
Ответ: решение есть; например, следующее: номер станции: 1 2 3 4 5
тарифный номер: 1 4 1 5 3
Замечание: тарифные номера разных станций могут совпадать.
|
Формат входных данных
В первой строке входных данных содержатся два целых числа: N — количество станций (2 ≤ N ≤ 100 000), и M — количество перегонов между ними (1 ≤ M ≤ N – 1). В последующих M строках записаны пары целых чисел a, b (a ≠ b, 1 ≤ a ≤ N, 1 ≤ b ≤ N), означающие наличие перегона между станциями a и b. За ними в отдельной строке записано единственное целое положительное число K — количество маршрутов электричек. В последующих K строках идут описания маршрутов электричек, по одному на строке. Каждое описание представляет собой последовательность целых чисел — номеров всех станций маршрута в порядке одного из двух возможных направлений следования электрички. Описание маршрута заканчивается числом 0.
Все номера станций в описании маршрута различны. Количество станций в каждом маршруте не менее двух. Любые две последовательные станции в маршруте каждой электрички соединены перегоном. Суммарное количество станций в описаниях всех маршрутов не превосходит 200 000. Могут быть станции и перегоны, через которые не проходит ни одна электричка.
Формат выходных данных
В первую строку выведите «NO», если искомого назначения тарифных номеров не существует. В противном случае в первую строку выведите «YES», а в следующей строке — N целых положительных чисел, где i-е число — тарифный номер i-й станции. Тарифный номер каждой станции должен находиться в диапазоне от 1 до N.
Если существует несколько решений, необходимо вывести любое из них.
| |
![]()
|
4/
2
|
|
Темы:
Обход в глубину
В развлекательном центре Е-города был установлен игровой автомат нового поколения. В автомат можно бросить монету и следить за её продвижением сверху вниз по разветвляющемуся лабиринту из трубок. В лабиринте есть \(n\) узлов, которые пронумерованы числами от 1 до \(n\). При бросании монета попадает в первый узел. Каждый узел лабиринта, кроме первого, имеет одну входящую сверху трубку, по которой монета может в него попасть. Из каждого узла выходит не более двух трубок, идущих вниз, одна из которых ведет налево, а другая "— направо. Каждая трубка имеет некоторую ширину. Монета проваливается в более широкую трубку, а в случае равенства ширины трубок "— в левую.
После прохождения монеты по трубке ширина этой трубки уменьшается на 1. Монета не может пройти по трубке ширины 0. Если монета достигла узла, из которого она не может дальше двигаться вниз, автомат останавливается и ждёт, когда в него бросят следующую монету.
Изначально в каждом узле лабиринта находится по игрушке. Когда монета попадает в узел первый раз, игрушка, находящаяся в этом узле, достаётся игроку, бросившему эту монету.
Панкрату понравилась игрушка, которая находится в узле с номером \(v\).
Требуется написать программу, которая определяет, сколько монет должен бросить в автомат Панкрат, чтобы получить игрушку из узла \(v\).
Формат входных данных
В первой строке задано число \(n\) — количество узлов в лабиринте. В последующих \(n\) строках заданы описания всех узлов, в \(k\)-й из этих строк описан узел с номером \(k\).
Описание \(k\)-го узла состоит из четырех целых чисел: \(a_k\), \(u_k\), \(b_k\), \(w_k\). Если из \(k\)-го узла выходит левая трубка, то \(a_k\) — номер узла, в который она ведет (\(k < a_k \leqslant n\)), а \(u_k\) — её ширина. Если левой трубки нет, то \(a_k = u_k = 0\). Если из \(k\)-го узла выходит правая трубка, то \(b_k\) — номер узла, в который она ведет (\(k < b_k \leqslant n\)), а \(w_k\) — её ширина. Если правой трубки нет, то \(b_k = w_k = 0\).
В последней строке задано целое число \(v\) (\(1 \leqslant v \leqslant n\)) — номер узла, в котором находится игрушка, понравившаяся Панкрату.
Гарантируется, что во все узлы, кроме первого, входит ровно одна трубка.
Формат выходных данных
Выходные данные должны содержать одно число — количество монет, которое необходимо бросить в автомат Панкрату, чтобы получить игрушку, которая находится в узле \(v\). Если получить выбранную игрушку невозможно, выведите число \(-1\).
Пояснение к примеру
В первом примере первая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 1, 3 и 4:
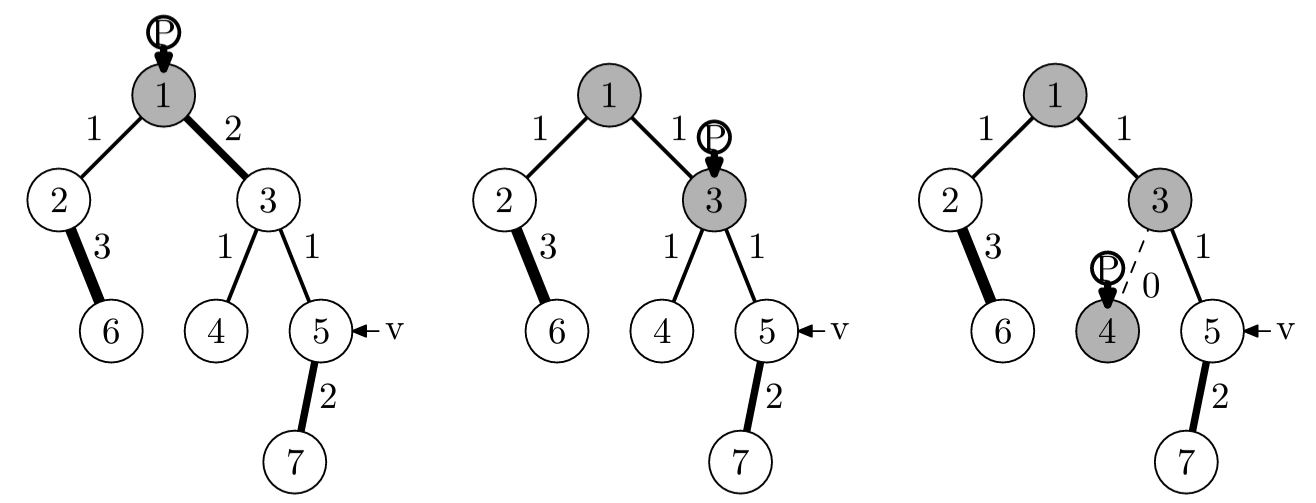
Вторая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 2 и 6:
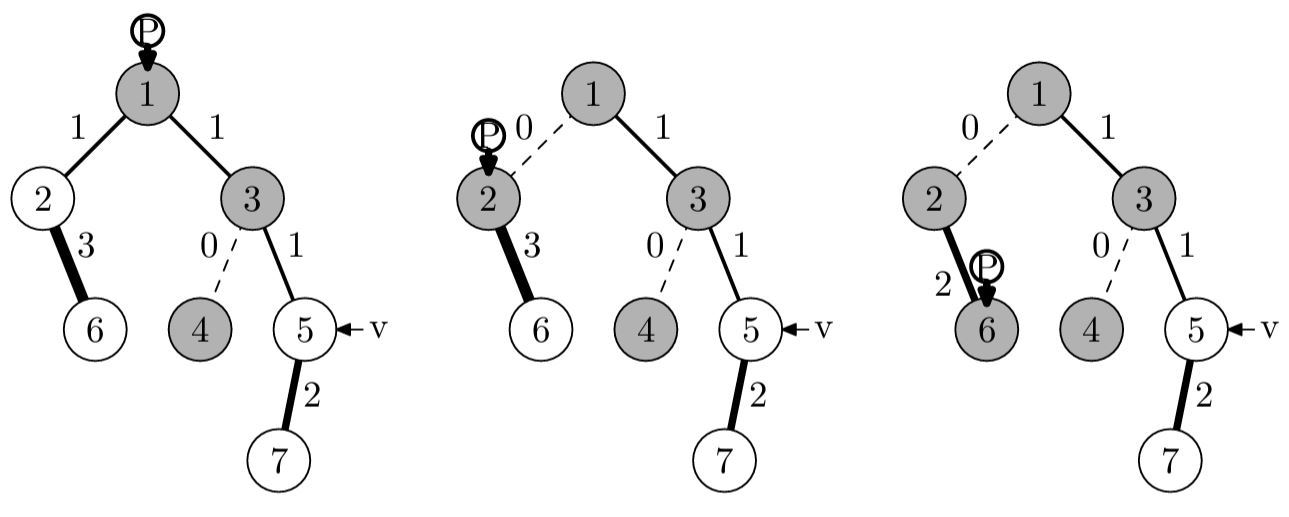
Третья монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 5 и 7:
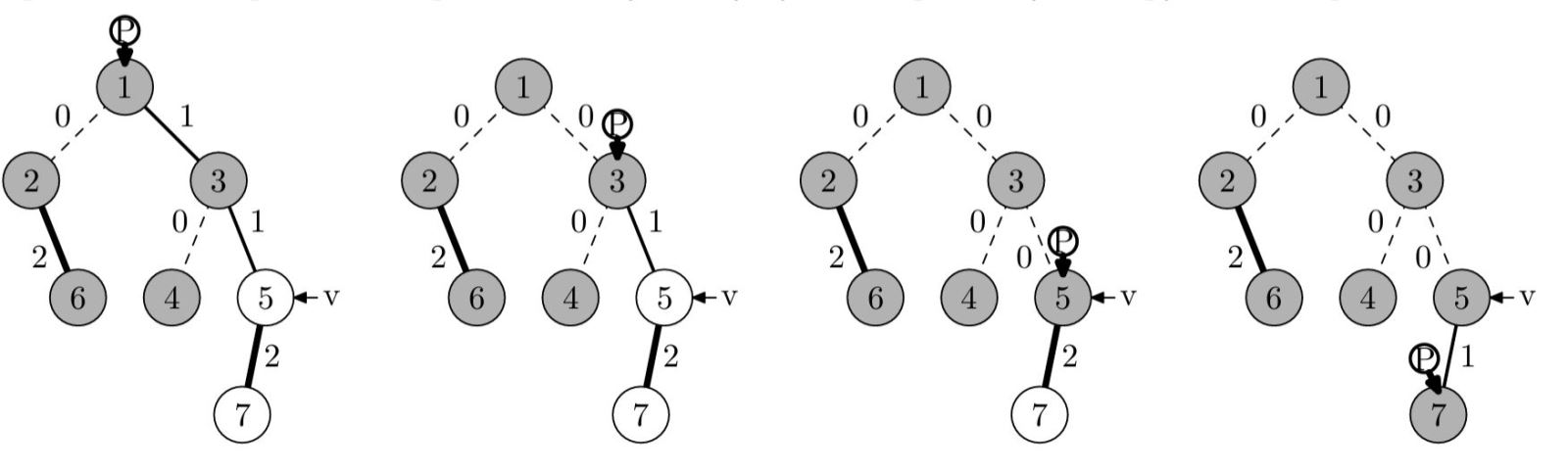
| |
![]()
|
5/
3
|
|