| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Рекурсия
В подземелье живут гномы. У них есть древняя традиция деления золота:
Когда гном получает N монет:
1. Если N = 0, гном грустит и ничего не делает
2. Если N = 1, гном оставляет монету себе и кричит "МОЁ!"
3. Если N > 1:
- Гном берёт себе 1 монету и кричит "МОЁ!"
- Остальные (N-1) монет делит пополам
- Левую половину (N-1)/2 отдаёт левому ученику-гному
- Правую половину (N-1) - (N-1)/2 отдаёт правому ученику-гному
- Каждый ученик делает то же самое по традиции
Подсчитайте, сколько раз прозвучит крик "МОЁ!" при делении N монет.
ВХОДНЫЕ ДАННЫЕ:
Одно число N (0 ≤ N ≤ 10^9) - начальное количество монет.
ВЫХОДНЫЕ ДАННЫЕ:
Одно число - сколько раз прозвучит "МОЁ!"
| |
![]()
|
/
|
|
Темы:
Рекурсия
Дана блок-схема алгоритма, реализованного в виде рекурсивно вызываемой функции:
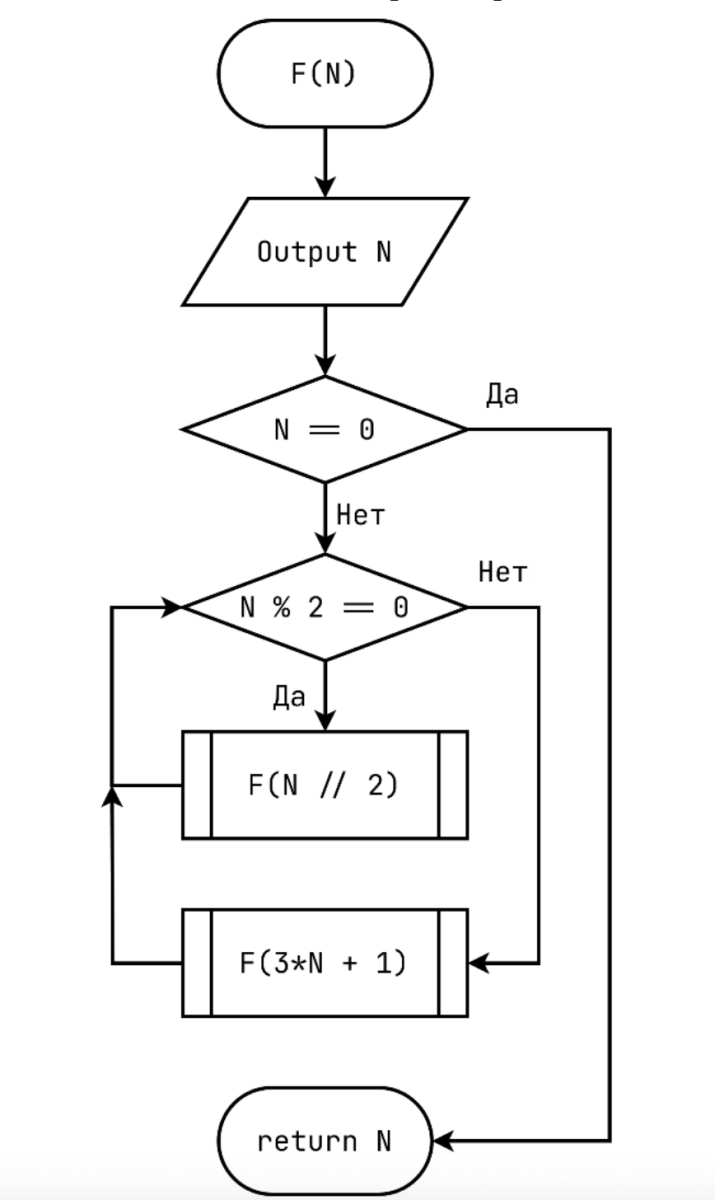
Определите сумму первых 1010 чисел, которые выведутся при запуске алгоритма с 𝑁 = −3159
| |
![]()
|
/
|
|
Темы:
Рекурсия
Разбирая старые задачи олимпиады, Петя наткнулся на алгоритм рекурсивного закрашивания растрового изображения. У Пети есть черно-белое (bitmap) изображение размером 13 на 13 пикселей. На изображении присутствует замкнутый контур, как приведено на рисунке. Пиксели внутри контура пронумерованы.

Традиционно для компьютерной графики, система координат имеет начало в верхнем левому углу, ось X направлена слева направо, а ось Y – сверху вниз.
Алгоритм рекурсивного закрашивания заключается в рекурсивном вызове процедуры «Закрасить», которой передаются два параметра – координаты X и Y пикселя.
Процедура Закрасить(X, Y), может быть описана следующим образом:
1. Если цвет пикселя с координатами (X, Y) белый, то:
a. Изменить цвет пикселя с этими координатами на черный;
b. Вызвать процедуру Закрасить(X+1, Y);
c. Вызвать процедуру Закрасить(X, Y+1);
d. Вызвать процедуру Закрасить(X-1, Y);
e. Вызвать процедуру Закрасить(X, Y-1);
2.Иначе завершить процедуру.
Известно, что последний закрашенный пиксель, перед завершением процедуры, имел номер 29. Сколько существует пикселей внутри контура, в которых можно исходно вызвать процедуру «Закрасить» так, чтобы получить такой результат?
В ответе укажите целое число.
| |
![]()
|
/
|
|
Темы:
Рекурсия
Рекуррентные последовательности
Дана блок-схема алгоритма, реализованного в виде рекурсивно вызываемой функции:

Известно, что 𝐴, 𝐵 и 𝐶 - натуральные числа и что 𝐴 < 𝐵 < 𝐶.
Петя вызывает эту функцию, передавая ей в качестве входного параметра натуральное число. Известно, что для некоторого 𝑘 функция возвращает следующие значения:
𝐹(𝑘) = 50890368413;
𝐹(𝑘 + 1) = 93601980590;
𝐹(𝑘 + 2) = 172160883161.
Определите значения 𝐴, 𝐵 и 𝐶, при которых это возможно. Если таких вариантов несколько, выберите вариант с наименьшей суммой 𝐴, 𝐵 и 𝐶. В ответе введите в указанном порядке значения 𝐴, 𝐵 и 𝐶, разделённые пробелом.
| |
![]()
|
/
|
|
Темы:
Рекурсия
Строка формируется из заглавных английских букв следующим образом
-
Начинаем с "A".
-
Каждый следующий шаг: к предыдущей строке приписываем новую строку, в которой каждый символ предыдущей строки сдвинут вправо на 2 по алфавиту (A→C, B→D, ..., Y→A, Z→B).
Вот первые четыре шага:
Шаг 1: A
Шаг 2: AС
Шаг 3: AССE
Шаг 4: ACCECEGG
Какой символ стоит на 50-й позиции после 7-го шага?
Первый символ слева стоит на позиции 1.
| |
![]()
|
/
|
|
Темы:
Рекурсия
Строка формируется из заглавных английских букв следующим образом
-
Начинаем с "A".
-
Каждый следующий шаг: к предыдущей строке приписываем новую строку, в которой каждый символ предыдущей строки сдвинут вправо на 1 по алфавиту (A→B, B→C и т. д. Z→A).
Вот первые четыре шага:
Шаг 1: A
Шаг 2: AB
Шаг 3: ABBC
Шаг 4: ABBCBCCD
Какой символ стоит на 100-й позиции после 8-го шага?
Первый символ слева стоит на позиции 1.
| |
![]()
|
/
|
|
Темы:
Рекурсия
Строки, состоящие из последовательностей цифр, формируются следующим образом. Первая строка состоит из одной единицы. Каждая из последующих строк создается следующим действием: берется предыдущая строка и после каждой ее цифры вставляется цифра на единицу большая и затем еще раз исходная цифра. Вот первые 3 строки, созданные по этому правилу:
(1) 1
(2) 121
(3) 121232121
(4) 121232121232343232121232121
Какая цифра будет стоять в позиции 1094 в строке (9)?
Первая цифра слева стоит на позиции 1
| |
![]()
|
/
|
|
Темы:
Рекурсия
Строки, состоящие из последовательностей цифр, формируются следующим образом. Первая строка состоит из четырех единиц. Каждая из последующих строк создается следующим действием: берется предыдущая строка и перед каждой ее цифрой вставляется цифра на единицу большая. Вот первые 3 строки, созданные по этому правилу:
(1) 1111
(2) 21212121
(3) 3221322132213221
Какая цифра будет стоять в позиции 479 в строке (9)?
Первая цифра слева стоит на позиции 1
| |
![]()
|
/
|
|
Темы:
Рекурсия
Строки, состоящие из последовательностей цифр, формируются следующим образом. Первая строка состоит из четырех единиц. Каждая из последующих строк создается следующим действием: берется предыдущая строка и после каждой ее цифры вставляется цифра на единицу большая. Вот первые 3 строки, созданные по этому правилу:
(1) 1111
(2) 12121212
(3) 1223122312231223
Какая цифра будет стоять в позиции 479 в строке (9)?
Первая цифра слева стоит на позиции 1
| |
![]()
|
/
|
|
Темы:
Рекурсия
Строки, состоящие из последовательностей цифр, формируются следующим образом. Первая строка состоит из четырех единиц. Каждая из последующих строк создается следующим действием: берется предыдущая строка и после каждой ее цифры вставляется цифра на единицу большая. Вот первые 3 строки, созданные по этому правилу:
(1) 1111
(2) 12121212
(3) 1223122312231223
Какая цифра будет стоять в позиции 100 в строке (9)?
Первая цифра слева стоит на позиции 1
| |
![]()
|
/
|
|
Темы:
Рекурсия
Перебор с возвратом
Рассмотрим все представления числа \(n\) в виде суммы различных целых возрастающих слагаемых: \(n = a_1 + a_2 + \ldots + a_k\), \(a_1 < a_2 < \ldots < a_k\).
Будем называть такое разбиение быстро возрастающим, если для него выполнено следующее условие: для любых трех подряд идущих слагаемых разница между большим и средним строго больше, чем между средним и меньшим, иначе говоря, \(a_{i+2} - a_{i+1} > a_{i+1} - a_i\).
Задано число \(n\). Выведите все его быстро возрастающие разбиения на слагаемые.
Формат входных данных
На ввод подается целое число \(n\) (\(1 \le n \le 100\)).
Формат выходных данных
Выведите все быстро возрастающие разбиения на слагаемые числа \(n\). Разбиения можно выводить в любом порядке. Выводите слагаемые в каждом разбиении, разделяя их знаком <<+>> без пробелов.
| |
![]()
|
41/
8
|
|
Темы:
Рекурсия
Ввести в символьной форме два многочлена от x с целыми коэффициентами и вывести их произведение в порядке убывания степеней - также в символьной форме.
Ограничения: степень исходных многочленов не более 10, коэффициенты исходных многочленов по модулю не более 104.
Входные данные
В двух строках находятся многочлены.
Выходные данные
В единственной строке выводится многочлен.
| |
![]()
|
3/
1
|
|
Темы:
Рекурсия
Игра для двух игроков определяется её деревом. Соперники делают ходы по очереди. Первый игрок начинает игру. Игра кончается или вничью, или победой одного из игроков. Листья дерева этой игры могут иметь значения, равные одному из трёх чисел: +1 - победа первого игрока, -1 - победа второго игрока, 0 - ничья. Ваша задача - определить, кто выиграет, если оба противника следуют правильной стратегии.
Входные данные
Узлы дерева пронумерованы последовательными целыми числами. Корень дерева всегда имеет номер 1. Первая строка входного файла содержит целое N - число узлов в дереве игры. Следующая N - 1 строка описывает узлы - одна строка для каждого узла (за исключением первого). Вторая строка содержит описание второго узла дерева, третья - третьего узла и т.д. Если узел является листом, первый символ строки - L, затем идёт пробел, затем номер родительского узла, ещё пробел и результат игры (+1 - победа первого игрока, -1 - победа второго, 0 - ничья). Если узел внутренний, то строка содержит N - первый символ, затем пробел и номер родительского узла. 2 <= N <= 1000.
Выходные данные
Выводится +1, если выигрывает первый игрок, -1, если второй, и 0 - в случае ничейного исхода.
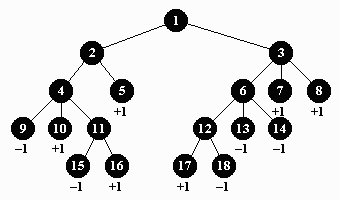
| |
![]()
|
1/
1
|
|
Темы:
Рекурсия
Головоломка "Ханойские башни" состоит из трех колышков, пронумерованных числами 1, 2, 3. На колышек 1 надета пирамидка из n дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного колышка на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку с колышка 1 на колышек 2 за минимальное число перекладываний.
Напишите программу, которая решает головоломку для данного числа дисков n.
Входные данные
Вводится 1 число n.
Выходные данные
Необходимо вывести последовательность перекладываний в формате "Disk 1 move from 1 to 2" (диск 1 переложить c колышка 1 на колышек 2), печатая по одной инструкции в строке. Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
| |
![]()
|
21/
9
|
|
Темы:
Рекурсия
Задачи на процедуры и функции
Напишите функцию быстрого возведения в степень. Количество действий должно быть пропорционально двоичному логарифму n.
Входные данные
Вводится 2 числа - a (вещественное) и n (целое неотрицательное).
Выходные данные
Необходимо вывести значение an.
| |
![]()
|
2/
2
|
|
Темы:
Динамическое программирование
Рекурсия
Жадный алгоритм
В сети магазинов <<Мир>> при оплате карточкой Weeza действует акция. При оплате покупки, состоящей не менее чем из \(10\) товаров, плата за самый дешевый товар не берется. Если товаров не меньше 20, то не оплачиваются уже два самых дешевых товара и т.д.
Например, при одновременной покупке \(17\) товаров, покупатель потратит сумму денег равную стоимости только \(16\) самых дорогих из них, а при покупке \(20\) и \(37\) товаров придется заплатить только за \(18\) и \(34\) самых дорогих товара, соответственно.
Миша хочет купить в магазине <<Мир>> \(n\) дисков с альбомами его любимой музыкальной группы. Подобрав подходящие диски, Миша выложил их на ленту в супермаркете в некотором порядке. Так как Миша не только меломан, но и математик, он понял, что ему, возможно, удастся сэкономить, если платить не за все \(n\) товаров одновременно, а разбить их на несколько покупок и оплатить каждую покупку отдельно. Миша решил привлекать к себе как можно меньше внимания и, в частности, не менять порядок товаров на ленте. Таким образом, Миша может только разбивать товары на ленте на группы подряд идущих и платить за каждую группу в отдельности.
Миша, конечно, математик, но вот с арифметикой у него всегда были проблемы. Помогите Мише и скажите, за какую минимальную стоимость он сможет купить \(n\) дисков, разбивая товары на ленте на группы подряд идущих товаров и оплачивая каждую группу отдельно. При этом разные группы могут быть разной длины.
Формат входных данных
В первой строке находится одно число \(n\) (\(1 \leq n \leq 100\,000\)) — количество дисков на ленте.
Следующая строка содержит \(n\) чисел \(a_i\) (\(1 \leq a_i \leq 10^9\)) — стоимости дисков в порядке расположения на ленте.
Формат выходных данных
Выведите наименьшую возможную стоимость покупки всех дисков с учетом акции при оптимальном разбиении дисков на группы.
Примечание
В первом примере Мише в любом случае придется оплатить все диски, так как суммарное количество товаров меньше \(10\).
Во втором тестовом примере оптимально во время первой покупки оплатить первые два диска, а за остальные диски заплатить во время второй покупки. Тогда не придется заплатить за диск стоимостью \(9\).
| |
![]()
|
6/
4
|
|
Темы:
Рекурсия
Недавно на кружке по математике Миша узнал про разбиения на слагаемые. Разбиением числа \(n\) на слагаемые называется представление его в виде суммы неубывающего набора натуральных чисел. Например, \(9=1+2+2+4\) является разбиением числа 9 на слагаемые.
Миша называет разбиение интересным, если никакие два слагаемых в наборе не равны и не отличаются ровно на 1. Так, например, разбиение, приведенное выше не является интересным, а разбиение \(9=1+3+5\) — является.
Помогите Мише вывести все интересные разбиения числа \(n\) на слагаемые.
Формат входных данных
На ввод подается одно целое число \(n\) (\(1 \le n \le 80\)).
Формат выходных данных
Выведите все интересные разбиения числа \(n\) на слагаемые. Разбиения можно выводить в любом порядке. Соблюдайте формат из примера.
| |
![]()
|
7/
5
|
|
Темы:
Динамическое программирование
Рекурсия
Рассмотрим разбиения целого положительного числа \(n\) в сумму целых положительных чисел. Будем называть разбиение непростым, если слагаемые в нем упорядочены по неубыванию, причем среди слагаемых нет простых чисел.
Например, для \(n=5\) существует два непростых разбиения: \(1+1+1+1+1\) и \(1+4\).
Задано число \(n\). Выведите все его непростые разбиения на слагаемые.
Формат входных данных
На вход подается число \(n\) (\(1 \le n \le 70\)).
Формат выходных данных
Выведите все непростые разбиения \(n\) на слагаемые. Слагаемые разделяйте знаком <<+>>. Не выводите пробелы. Разбиения можно вывести в любом порядке.
| |
![]()
|
45/
13
|
|
Темы:
Рекурсивный перебор
Рекурсия
Перебор с возвратом
Даны два целых числа n и k, выведите все возможные комбинации из k чисел, выбранных из диапазона [1, n]. Порядок элементов в одной комбинации не важен. То есть комбинация (1, 2, 3) и (3, 2, 1) считается одинаковой.
Выведите на экран все такие комбинации в лексикографическом порядке.
Входные данные
В первой строке записано целое число n, во второй - целое число k.
Ограничения
Выходные данные
Выведите в лексикографическом порядке все возможные комбинации из k чисел, выбранных из диапазона [1, n]. Каждая комбинация чисел должна выводиться в отдельной строке, числа в одной комбинации разделяются одним пробелом.
| |
![]()
|
111/
61
|
|
Темы:
Рекурсивный перебор
Перебор с возвратом
Рекурсия
XOR-cумма массива определяется как побитовое XOR всех его элементов или 0, если массив пуст.
Например, XOR-сумма массива [2,5,6] равна 2 XOR 5 XOR 6 = 1.
Для заданного массива nums, верните сумму всех XOR-сумм для каждого подмножества nums.
Примечание: подмножества, состоящие из одинаковых элементов, считаются различными и должны подсчитываться несколько раз.
Массив a является подмножеством массива b, если a может быть получено из b путем удаления некоторых (возможно не удалением никаких) элементов b.
Входные данные
Программа получает на вход в первой строке натуральное число n - количество элементов массива nums. Во второй строке записаны n чисел numsi.
Ограничения
1 <= n <= 121 <= numsi <= 20
Выходные данные
Выведите ответ на задачу.
Пояснения к тестовым примерам
В первом примере
В [1,3] существует 4 подмножества:
- Пустое подмножество имеет XOR-сумму 0.
- [1] имеет XOR-сумму, равную 1.
- [3] имеет XOR-сумму, равную 3.
- В [1,3] сумма XOR равна 1 XOR 3 = 2.
0 + 1 + 3 + 2 = 6
Во втором примере
В [5,1,6] 8 подмножеств:
- Пустое подмножество имеет XOR-сумму 0.
- [5] имеет XOR-сумму, равную 5.
- [1] имеет XOR-сумму, равную 1.
- [6] имеет XOR-сумму, равную 6.
- [5,1] имеет XOR-сумму 5 XOR 1 = 4.
- [5,6] имеет XOR-сумму 5 XOR 6 = 3.
- [1,6] имеет XOR-сумму 1 XOR 6 = 7.
- [5,1,6] имеет XOR-сумму 5 XOR 1 XOR 6 = 2.
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28
| |
![]()
|
53/
30
|
|