| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Арифметические алгоритмы (Теория чисел)
В известной школе прошёл урок физкультуры. Как полагается, всех построили в шеренгу и попросили рассчитаться на <<первый–\(k\)-й>>, где \(k > 1\).
Как известно, расчёт на <<первый–\(k\)-й>> происходит следующим образом: первые \(k\) человек имеют номера \(1, 2, 3, \ldots, k\), следующие \(k - 1\) человек имеют номера \(k - 1, k - 2, \ldots, 1\), следующие \(k - 1\) человек имеют номера \(2, 3, \ldots, k\) и т.д. Таким образом, расчёт повторяется через каждые \(2k - 2\) позиции. Примеры расчёта приведены в разделе <<Замечание>>.
Мальчик Вася постоянно всё забывает. Например, он забыл число \(k\), описанное выше. Но он помнит позицию, которую занимал в шеренге, а также какой номер он получил при расчёте. Помогите Васе понять, сколько натуральных чисел \(k\) подходят под данные ограничения.
Обратите внимание, что не существует расчёта для \(k = 1\).
Формат входных данных
Первая строка содержит одно целое число \(n\) (\(2 \leq n \leq 10^9\)) — позиция Васи в ряду в нумерации, начинающейся с \(1\).
Вторая строка содержит одно целое число \(x\) (\(1 \leq x < n\)) — номер, который Вася получил при расчёте.
Формат выходных данных
Выведите единственное целое число — количество различных \(k > 1\), которые подходят под данные ограничения.
Можно доказать, что при данных ограничениях ответ является конечным.
Примечание
В первом примере подходят \(k\) равные \(2, 3, 5, 6\).
Пример расчёта для этих \(k\):
| \(2\) |
\(1\) |
\(2\) |
\(1\) |
\(2\) |
\(1\) |
\(2\) |
\(1\) |
\(2\) |
\(1\) |
\(2\) |
| \(3\) |
\(1\) |
\(2\) |
\(3\) |
\(2\) |
\(1\) |
\(2\) |
\(3\) |
\(2\) |
\(1\) |
\(2\) |
| \(5\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(4\) |
\(3\) |
\(2\) |
\(1\) |
\(2\) |
| \(6\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(5\) |
\(4\) |
\(3\) |
\(2\) |
| |
![]()
|
14/
4
|
|
Темы:
Арифметические алгоритмы (Теория чисел)
Число называется совершенным, если оно равно сумме всех своих делителей, меньших его самого. Требуется найти все совершенные числа от M до N.
Входные данные
В первой строке находятся разделённые пробелом числа M и N. M и N целые, 1 <= M <= N <= 109, (N - M) * sqrt(N) <= 107.
Выходные данные
В каждой строке вывести по одному числу в порядке возрастания. Если совершенных чисел в промежутке нет, вывести "Absent".
| |
![]()
|
4/
3
|
|
Темы:
Арифметические алгоритмы (Теория чисел)
Дан массив \(A = [a_1, a_2, \ldots, a_n]\), содержащий \(n\) натуральных чисел.
Требуется раскрасить элементы массива в два цвета таким образом, чтобы не существовало двух элементов \(x\) и \(y\) одного цвета, таких что \(x\) нацело делился на \(y\) и выполнялось равенство \(\frac{x}{y} = p\), где \(p\) — простое число. Гарантируется, что такая раскраска существует.
Напомним, что целое число \(p > 1\) называется простым, если оно имеет ровно два делителя: \(1\) и \(p\).
Формат входных данных
Первая строка содержит одно целое число \(n\) (\(1 \le n \le 100\,000\)) — количество элементов в массиве.
Вторая строка содержит \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 10^6\)) — элементы массива.
Формат выходных данных
Выведите описание разбиения массива на два множества в следующем формате.
Выведите \(n\) целых чисел, \(i\)-е из которых равняется \(1\), если элемент \(a_i\) надо раскрасить в первый цвет и \(2\), если элемент \(a_i\) надо раскрасить во второй цвет.
Если существует несколько подходящих раскрасок, вы можете вывести любую из них.
В первом примере есть два элемента первого цвета: \(2\) и \(3\), и два элемента второго цвета: \(1\) и \(4\). Элементы первого цвета не делятся нацело друг на друга. \(4\) нацело делится на \(1\), но их отношение не является простым числом.
| |
![]()
|
49/
5
|
|
Темы:
Конструктив
Арифметические алгоритмы (Теория чисел)
Олимпиады бывают не только личные, но и командные. В командной олимпиаде по программированию обычно принимают участие команды из трёх человек, которым предоставляется один компьютер и один комплект условий задач, причём задач обычно существенно больше, чем в личных олимпиадах.
Условие каждой из задач помещается на одной, двух или трёх страницах. При этом условие может быть напечатано на двух сторонах одного листа, но для удобства команд на одном листе может располагаться условие только одной из задач. Для экономии бумаги, если условие задачи занимает две страницы, оно должно быть напечатано на двух сторонах одного листа, а если из трёх страниц - на двух сторонах одного листа и на одной стороне другого листа, вторая сторона которого останется чистой. При этом можно напечатать первую страницу такой задачи отдельно на чистом листе, а оставшиеся две страницы - на одном листе или, наоборот, первые две страницы распечатать на одном листе, а третью - на чистом листе. Задачи и все их страницы печатаются последовательно.
Условия всех задач распечатываются на принтере в виде нескольких последовательных заданий. Для каждого задания необходимо задать диапазон печати: номера первой и последней страниц, которые будут напечатаны в этом задании (будут напечатаны все страницы в этом диапазоне), а также тип печати - односторонняя или двусторонняя.
Вам необходимо минимизировать количество заданий для печати условий.
Формат входных данных
Первая строка входных данных содержит целое число n (1 ≤ n ≤ 106) - количество задач в олимпиаде.
Вторая строка входных данных содержит целое число n (1 ≤ xi ≤ 3) - количество страниц в i-й задаче.
Формат выходных данных
Выведите единственное число - минимальное количество последовательных диапазонов, каждый из которых можно напечатать одной командой односторонней или двусторонней печати так, что условия всех задач будут напечатаны в удобном для командной олимпиады виде.
Замечание
В первом примере на олимпиаду предложены 4 задачи, условия которых состоят из 1, 3, 2 и 1 страниц соответственно. Всего необходимо распечатать 7 страниц. Их можно распечатать за два задания: cтраницы 1-2 - односторонней печатью (это единственная страница первой задачи и первая из трёх страниц второй задачи), оставшиеся страницы 3-7 - двусторонней.
Во втором примере на олимпиаду предложены 2 задачи, условия которых состоят из 3 страниц каждая. Всего необходимо распечатать 6 страниц. Их можно распечатать за два задания: cтраницы 1-1- односторонней печатью (это первая из трёх страниц первой задачи), оставшиеся страницы 2-6 - двусторонней. При этом в первой задаче первая страница будет напечатана на одной стороне, потому что она напечатана односторонней печатью, а во второй задаче последняя страница будет напечатана на одной стороне, потому что в этом задании нечётное число страниц печатается на двух сторонах, поэтому вторая сторона этого листа будет пустой.
| |
![]()
|
63/
13
|
|
Темы:
Алгоритмы на графах
Арифметические алгоритмы (Теория чисел)
Применение обхода в глубину
Обход в глубину
Дано дерево на n вершинах (связный неориентированный ациклический граф c n−1 рёбрами), где у каждого ребра есть вес w. Назовём простой путь длины k возрастающим , если существует такое целое x>=2, что вес первого ребра пути делится на x, второго ребра — делится на x2, ……, вес k-го ребра делится на xk.
Требуется найти максимальную длину k возрастающего пути, где k — количество рёбер в нём.
Входные данные
В первой строке вводится единственное целое число n (1 <= n <= 100000) - число вершин в дереве.
В следующих n−1 строках вводятся по три целых числа u, v, w ( 1<= v <= n, 1<= w <= n, u ≠ v, 1 <= w <= 107) - номера вершин, которые соединяет очередное ребро, и его вес.
Выходные данные
Выведите одно целое число k - максимальную длину возрастающего пути.
Примечание
Простым путем называется такой путь, что все вершины в нем различны.
В 1-м примере есть путь длины 2: 3 — 1 — 2. Тогда для него подходящий x = 2. Можно показать, что возрастающего пути большей длины не существует.
Во 2-м примере есть путь длины 3: 3 — 4 — 5 — 6. Тогда для него подходящий x = 2. Можно показать, что возрастающего пути большей длины не существует.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 2 8
1 3 6
1 4 3
|
2
|
| 2 |
6
1 2 2
2 3 4
3 4 2
4 5 4
5 6 8
|
3
|
| |
![]()
|
5/
2
|
|
Темы:
Циклы
Арифметические алгоритмы (Теория чисел)
Сегодня мальчик Саша на уроке математики узнал про фракталы. Учитель показывал так называемую «кривую дракона». Она представляет собой геометрическую фигуру, которая строится следующим образом: на первом шаге проводится отрезок из начала координатной плоскости в точку (0; 1). Далее на каждом шаге из конца фрактала повторяется уже нарисованная часть фигуры, повернутая на 90 градусов против часовой стрелки (см. рисунок).
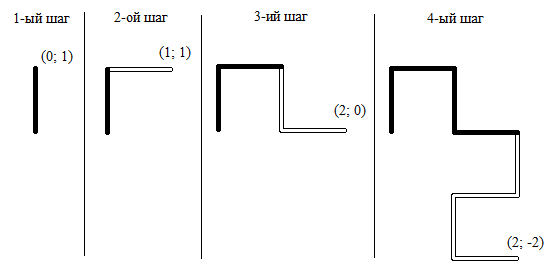
После уроков Саша попробовал сам изобразить «кривую дракона», и теперь он хочет знать, в какой точке координатной плоскости он закончил рисовать фрактал, проделав описанные выше N шагов. Требуется написать программу, которая по заданному числу N определяет координаты конца фрактала после выполнения N шагов.
Входные данные
Вводится одно целое число N (1 <= N <= 30).
Выходные данные
Выведите два числа через пробел - координаты конца фрактала.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 1 |
| 2 |
4 |
2 -2 |
| |
![]()
|
64/
24
|
|
Темы:
Остатки
Арифметические алгоритмы (Теория чисел)
На детском празднике дети водили хороводы. Как только музыка закончила играть, дети всё ещё стояли в кругу. Тут Лена вспомнила, что родители дали ей коробку с k конфетками «Wilky May». Лена не жадина, поэтому она решила раздать все свои конфетки друзьям из хоровода. Лена знает, что некоторые её друзья сладкоежки, а некоторые нет. Сладкоежки берут из коробки две конфетки, если в коробке есть хотя бы две конфетки, а иначе берут одну. Остальные друзья Лены всегда берут ровно одну конфетку из коробки.
Чтобы начать раздавать конфетки, Лена вышла из хоровода, после чего в хороводе остались n ее друзей. Чтобы раздавать конфетки было проще, Лена присвоила каждому другу в хороводе номер в порядке по часовой стрелке, начиная с её лучшего друга Ромы, который получил номер 1.
Лена дала коробку другу, который получил номер l, после чего каждый друг Лены, начиная с друга с номером l, брал конфетки из коробки и передавал коробку следующему в порядке по часовой стрелке другу. После того, как друг с номером r взял конфетки, в коробке конфеток не осталось. Обратите внимание, что возможно, что некоторые друзья Лены брали конфетки из коробки несколько раз, то есть коробка могла пройти несколько полных кругов по хороводу.
Лена не знает, кто из ее друзей сладкоежки, но ее интересует, сколько максимум из её друзей могут быть сладкоежками. Если же такой ситуации не могло случиться, и Лена ошиблась в своих наблюдениях, сообщите ей об этом.
Входные данные
В единственной строке задаются четыре целых числа n, l, r, k (1 ≤ n, k ≤ 1011 , 1 ≤ l, r ≤ n ) — количество детей в хороводе, номер друга, которому Лена отдала коробку конфет, номер друга, который взял последнюю конфетку, и количество конфет в коробке, соответственно.
Выходные данные
Выведите одно целое число — максимально возможное количество сладкоежек среди друзей Лены или « -1 » (без кавычек), если Лена ошиблась в своих наблюдениях.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
4 1 4 12 |
2 |
Любые два друга могут быть сладкоежками, тогда каждый два раза получит коробку конфет и последним, кто возьмёт конфету, будет четвёртый человек. |
| 2 |
5 3 4 10 |
3 |
Сладкоежками могут быть любые три друга, кроме друга, стоящего на третьем месте. |
| 3 |
10 5 5 1 |
10 |
Только один друг возьмёт одну конфетку, но он может быть сладкоежкой, просто он не может взять две конфеты. Все остальные в кругу тоже могут быть сладкоежками, но они не могут взять ни одной конфеты. |
| 4 |
5 4 5 6 |
-1 |
Лена ошиблась и такой ситуации быть не могло. |
| |
![]()
|
3/
2
|
|
Темы:
Арифметические алгоритмы (Теория чисел)
Рассмотрим N-домино. В таком домино каждая костяшка состоит из двух половинок, на каждой из которых нарисовано от 0 до N точек. Полный комплект костяшек такого домино содержит все возможные костяшки, каждую — по одному разу. Например, для N=2 в комплект войдут следующие костяшки: (0,0), (0,1), (0,2), (1,1), (1,2) и (2,2)
Напишите программу, которая по заданному N определит, сколько всего точек изображено на всех костяшках полного комплекта N-домино.
Входные данные
Вводится натуральное число N (1<=N<=30).
Выходные данные
Программа должна напечатать одно число - общее количество точек на всех костяшках полного комплекта N-домино.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
12 |
| |
![]()
|
129/
56
|
|
Темы:
Рекурсия
Целые числа
Арифметические алгоритмы (Теория чисел)
Последовательность 011212201220200112… строится следующим образом: сначала пишется 0, затем повторяется следующее действие: уже написанную часть приписывают справа с заменой 0 на 1, 1 на 2, 2 на 0, и т.д.
Требуется написать программу, которая по заданному натуральному числу N определяет, какое число стоит на N-ом месте.
Входные данные
Дано натурально число число N (1 ≤ N ≤ 1018).
Выходные данные
Выведите число, которое стоит на k-ом месте в последовательности.
| |
![]()
|
34/
4
|
|
Темы:
Арифметические алгоритмы (Теория чисел)
Линейный поиск
Вещественные числа
В лаборатории теории чисел одного университета изучают связь между
распределением квадратов и кубов натуральных чисел.
Пусть задано целое неотрицательное число k. Рассмотрим множество натуральных
чисел от a до b, включительно. Будем называть k-плотностью этого множества количество
пар натуральных чисел x и y, таких, что a ≤ x2 ≤ b, a ≤ y3 ≤ b, причем |x2– y3| ≤ k.
Например, 2-плотность множества натуральных чисел от 1 до 30 равна 3, так как
подходят следующие пары:
x = 1, y = 1, |x2– y3| = |1 – 1| = 0;
x = 3, y = 2, |x2– y3| = |9 – 8| = 1;
x = 5, y = 3, |x2– y3| = |25 – 27| = 2.
Требуется написать программу, которая по заданным натуральным числам a и b, а
также целому неотрицательному числу k, определяет k-плотность множества натуральных
чисел от a до b, включительно.
Формат входных данных
Входные данные содержат три строки. Первая строка содержит натуральное число a,
вторая строка содержит натуральное число b, третья строка содержит целое неотрицательное
число k (1 ≤ a ≤ b ≤ 1018, 0 ≤ k ≤ 1018).
Формат выходных данных
Выходные данные должны содержать одно целое число: искомую k-плотность
множества натуральных чисел от a до b, включительно.
| |
![]()
|
72/
6
|
|
Темы:
Арифметические алгоритмы (Теория чисел)
Функция Эйлера
Дробь \({m \over n}\) называется правильной несократимой, если \(0 < m < n\) и \(НОД (m, n) = 1\). Найдите количество правильных несократимых дробей со знаменателем n.
Входные данные
В первой строке задается число знаменателей для которых надо найти количество правильных несократимых дробей N (\(N <=100\)). Каждая последующая строка число n (\(n < 10^9\)).
Выходные данные
Для каждого n в отдельной строке вывести ответ на поставленную задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
23
23456
7
17
|
22
11712
6
16 |
| |
![]()
|
441/
210
|
|
Темы:
Вывод формулы
Циклы
Арифметические алгоритмы (Теория чисел)
Маленький Вася очень любит числа, а особенно сильно он любит интересные числа. Вася считает число x интересным, если сумма квадратов его цифр делится на число 7. Например, число 123 -
интересное, потому что 1 2 + 2 2 + 3 2 = 14 делится на 7, а число 16 - нет, потому что 1 2 + 6 2 = 37 не делится на 7. Однажды Вася увидел на доске число x, он сразу же захотел узнать величину минимального интересного числа, которое строго больше чем x. Так как Вася еще слишком юн, он обратился к вам за помощью в решение этой задачи.
Формат входных данных
Во входном файле содержится единственное целое число x - число, написанное на доске 0<= x <= 105
Формат выходных данных
В единственную строку выходного файла выведите минимальное интересное число, которое строго больше чем x.
| |
![]()
|
168/
60
|