Вещественные числа

Что выведет код?

a = 3
b = float(a)
print(b)

Выбери верный вариант ответа

1. 3
2. 3.0

На стенде идет проверка нового оборудования. Установка включается на N минут. Каждую минут снимаются показания с датчика давления. Известно номинальное (нормальное) значение давления A, а также допустимое отклонение от него ε. Определите, сколько раз за время проверки отклонение от номинального значения A превысило значение ε.

Входные данные
На первой строке вводится A – вещественное число – номинальное значение давления.
На второй строке – ε – вещественное число – допустимое отклонение.
На третьей строке – N – натуральное число – время тестирования.
На последующих N строчках вводятся вещественные числа – показания датчика давления.
Все числа положительные и не превосходят 1 000 000.
Выходные данные
Количество недопустимых, т.е. превышающих ε, отклонений от номинального значения A за время проверки.

Какое утверждение о типе данных REAL в SQLite является верным?

Ответы:

1. REAL используется для хранения целых чисел.
2. В SQLite значения REAL хранятся в формате 8-байтового числа с плавающей запятой.
3. REAL — это текстовый тип данных, применяемый для хранения строк.
4. Значения типа REAL в SQLite могут хранить только положительные числа.

Даны три действительных числа: a, b, c. Проверьте, выполняется ли равенство a + b = c . Если равенство выполняется, выведите YES, если не выполняется, выведите NO.

Входные данные
Числа a, b, c –  действительные, положительные, не превосходят 10 и заданы не более, чем с 7 знаками после точки.

Выходные данные
Выведите результат сравнения.

По российский правилам числа округляются до ближайшего целого числа, а если дробная часть числа равна 0.5, то число округляется вверх.

Дано неотрицательное число x, округлите его по этим правилам. Обратите внимание, что функция round не годится для этой задачи!

Определите, какого типа будет переменная d после выполнения фрагмента программы?

a = 7
b = 3.0
d = a * b

1) int
2) float
3) str

В первый день спортсмен пробежал x километров, а затем он каждый день увеличивал пробег на 70% от предыдущего значения. По данному числу y определите номер дня, на который суммарный пробег спортсмена составит не менее y километров.

Входные данные
На вход программа получает два действительных числа x и y . Числа положительные, действительные, не превосходят 1000, заданы с точностью до шести знаков после запятой.
Внимание! В некоторых тестах оба числа находятся на одной строке, а в некоторых — на разных!

Выходные данные
Программа должна вывести единственное целое число.

В первый день спортсмен пробежал x километров, а затем он каждый день увеличивал пробег на 70% от предыдущего значения. По данному числу y определите номер дня, на который пробег спортсмена составит не менее y километров.

Входные данные
На вход программа получает два действительных числа x и y. Числа положительные, действительные, не превосходят 1000, заданы с точностью до шести знаков после запятой.

Выходные данные
Программа должна вывести единственное целое число.

Для заданного в 10-й с/с дробного числа требуется определить разницу длин целой и дробной части этого числа в 5-й с/с при переводе с точностью до 8 разрядов.
Входные данные
положительное число в 10-й с/с, целая и дробная часть которого не превышают 8 разрядов каждая. Целая и дробная части разделяются точкой. Дробная часть может отсутствовать.
Выходные данные
неотрицательное целое число - разница между количеством разрядов целой и дробной части в пятеричной системе счисления.

Примеры

№	Входные данные	Выходные данные	Примечание
1	8.4	1	8.410=13.25, количество разрядов целой части на 1 больше, чем дробной
2	1.5	7	1.510=1.(2)5=1.222222225, в 5-й с/с дробь не имеет конечного представления, поэтому ограничиваем длину 8 дробными разрядами

Напишите программу, которая вычисляет длину окружности через площадь круга.


Длину окружности по известной площади круга можно вычислить по формуле :
\(L=\sqrt{S4\pi}\) ,
где
\(\pi\) - число пи;
\(S\) - площадь круга.

Вы можете использовать встроенные константы для получения точного значения числа Пи.
На С++ необходимо в начале программы прописать строчку

#define _USE_MATH_DEFINES

На Python можно использовать константу из математической библиотеки
math.pi

Формат входных данных
На вход подается одно вещественное число - площадь круга S (1 <= S <= 10³).

Формат выходных данных
Выведите на экран длину окружности. Ваш ответ будет проверен с точностью до 6 знаков после запятой.

Дано положительное вещественное число. Выведите его первую цифру после десятичной точки.

Формат входных данных
На вход подается вещественное число.

Формат выходных данных
Выведите ответ на задачу.

Незнайка и Гунька решили встретиться, чтобы сходить в гости к Кнопочке. Они выбежали одновременно из своих домов навстречу друг к другу. Незнайка бежал со скоростью V1 м/с, Гунька со скоростью V2 м/с. Через сколько секунд они встретятся, если расстояние между их домами S метров.

Формат входных данных
На вход программе подаются три вещественных числа S, V1, V2, каждое на отдельной строке.

Формат выходных данных
Выведите ответ на задачу с точностью не менее 6 знаков после запятой.
 

Примеры

№	Входные данные	Выходные данные
1	100.0 15.0 20.0	2.857142857142857

Напишите программу, которая считывает длины двух катетов в прямоугольном треугольнике и выводит его площадь.


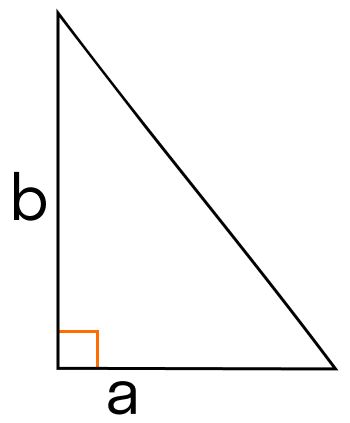
Площадь прямоугольного треугольника можно найти по формуле: \(S = {1 \over 2} \cdot a \cdot b\),
где a, b - длины катетов.


Формат входных данных
На вход программе подаётся два вещественных числа – длины катетов (a, b), каждое на отдельной строке (1 <= a, b <= 10⁴).

Формат выходных данных
Программа должна вывести одно число - площадь треугольника с точностью не менее трех знаков после запятой.

Питание школьника, при грамотной организации, должно обеспечивать содержание белков, жиров и углеводов в соотношении 10%:30%:60% (допускается погрешность +/- 1%). Детский лагерь составляет меню, состоящее из N различных продуктов. Для каждого продукта известна энергетическая ценность в белках (P), жирах (F) и углеводах (C), а также количество каждого вида продукта в меню (K).

Определите, является ли составленное меню сбалансированным или нет.


Входные данные
Программа получает на вход несколько строк. В первой строке записано число натуральное число N (N <= 100) количество различных продуктов. В каждой из следующих N строк записаны по 4 числа: Pi, Fi, Ci и Ki. Все числа вещественные, не превосходят 10³.

Выходные данные
Выведите YES, если меню сбалансированное, и NO в противном случае. 
 
 

Примеры

№	Входные данные	Выходные данные
1	3 0 1 1 2 1 2 7 1 3 7 13 1	YES

Дано верное равенство вида a₁+a₂+…+a_N=b₁+b₂+…b_M, где a₁,a₂,…,a_N, b₁,b₂,…,b_M – некоторые действительные (не обязательно целые) числа. Требуется «округлить» это равенство, т.е. получить новое верное равенство c₁+c₂+…+c_N=d₁+d₂+…+d_M, где c₁,c₂,…,c_N,d₁,d₂,…,d_M — целые числа, и при этом c₁ получено округлением числа a₁ до целого вверх или вниз (так, например, число 1.7 разрешается округлить как до 1, так и до 2), c₂ получено округлением a₂, …, c_N – округлением a_N, d₁ – округлением b₁, …, d_M – округлением b_M. Если какое-то из чисел в исходном равенстве было целым, оно должно остаться без изменений.

Входные данные
Во входном файле задано сначала число N, затем N чисел a₁, a₂, …, a_N, затем число M, затем числа b₁, b₂, …, b_M. Каждое число задается на отдельной строке. M и N – натуральные числа, не превышающие 1000. Остальные числа — вещественные, каждое из них по модулю не превышает 1000 и содержит не более 6 цифр после десятичной точки. При этом a₁+a₂+…+a_N=b₁+b₂+…b_M.

Выходные данные
Если «округлить» равенство можно, то в выходной файл выведите сначала числа c₁,c₂,…,c_N, а затем числа d₁,d₂,…,d_M. Все числа должны быть целыми и выведены без десятичной точки. Числа должны разделяться пробелами или переводами строки. Если решений несколько, выведите любое из них.

Если округлить исходное равенство до верного целочисленного равенства невозможно, выведите одно число 0.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	3 0.15 -3.000 2.7 1 -0.15	1 -3 2 0	Обратите внимание, что число –3 может округляться только в –3, в то время как 0.15 можно округлить как до 0, так и до 1, 2.7 – до 2 или до 3, –0.15 – до –1 или до 0. Приведенное решение не является единственным: так же верным является, например, такое округление: 1+(–3)+2=0
2	2 1.7 2.5 3 1 2.000 1.20	2 2 1 2 1	Приведенное решение 1+3=1+2+1 не является единственным. Верными ответами также являются 2+2=1+2+1 и 2+3=1+2+2.
3	1 0.5 1 0.5	0 0	Здесь верными являются как ответ 1=1, так и 0=0.

Начались каникулы, и Максим приехал в гости к бабушке и дедушке, но вовсе не в деревню, как вы, вероятно, подумали. Бабушка и дедушка Максима живут в очень культурном городе с легендарно плохой погодой — тут очень часто идет дождь.

Вот и сейчас стоило Максиму выйти из здания вокзала, как начался ливень. Зонтик, согласно всем законам подлости, лежит у него на дне чемодана, и лезть за ним совсем не хочется. Да и вот же — совсем рядом есть автобусная остановка, под которой можно укрыться от дождя. Нужно всего лишь перейти улицу, и все! «Не бывает все так просто», — пришло в голову Максиму. И действительно — не бывает.

Дело в том, что на улице, которая отделяет Максима от остановки, меняют асфальт. Старый слой асфальта уже сняли (там теперь ямы, поэтому пройти там невозможно), и теперь по улице, приближаясь к Максиму, со скоростью v2 м/мин мужественно ползет асфальтоукладчик, оставляя за собой новый, аккуратно уложенный асфальт. Правда, прежде, чем по новому асфальту можно будет ходить, он должен остывать T минут. Асфальтоукладчик только что начал работу, поэтому весь асфальт за ним был залит еще вчера и уже успел остыть.

Конечно же, Максим не хочет мокнуть, поэтому он пытается оказаться на другой стороне улицы как можно быстрее. Он бегает со скоростью v1 м/мин. Известна ему и ширина улицы — L м. Максим может ходить вдоль улицы по тротуару сколько ему хочется. Находиться на проезжей части он хочет как можно меньше, поэтому переходит улицу он только перпендикулярно.

Входные данные
Даны целые числа L, D, T, v1, v2 — ширина улицы, расстояние до асфальтоукладчика, время, которое остывает асфальт (в минутах), скорость Максима и скорость асфальтоукладчика. (1 ≤ L ≤ 100, 1 ≤ D ≤ 100, 1 ≤ T ≤ 100, 1 ≤ v1 ≤ 100, 1 ≤ v2 ≤ 100).

Выходные данные
Выведите одно число — время в минутах, которое понадобится Максиму, чтобы оказаться на другой стороне улицы.

Примеры

№	Входные данные	Выходные данные
1	4 9 3 2 1	6.0
2	1 1 1 3 1	0.666666666667

Первая строка входного файла содержит число n. Вам нужно вывести целое число m, где m - округленное до целого число n.
Пример.

Input	Output
3,2	3
-5,6	-6

Напишите программу, которая вычисляет квадратный корень введенного с клавиатуры числа, с точностью до трех знаков после запятой. 
Пример
Входные данные
25
Выходные данные
5.000

Напишите программу, которая вычисляет квадратный корень введенного с клавиатуры числа, с точностью до трех знаков после запятой. 
Пример входных и выходных данных.

Входные данные	Выходные данные
0.01002001	0.1

Напишите программу, которая вычисляет квадратный корень введенного с клавиатуры числа, с точностью до трех знаков после запятой. 
Пример
Входные данные
25
Выходные данные
5.000