| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Бинарный поиск по ответу
Вывод формулы
Трое друзей — Аня, Боря и Саша — пришли на детскую площадку, чтобы покачаться на качеляхбалансире. Качели представляют собой длинную балку, закреплённую в центре, на которую дети садятся с разных концов.

Массы детей равны A, B и C кг. Чтобы держать баланс на качелях, разница масс на двух концах качелей должна быть не более D кг. Друзьям повезло: рядом с площадкой оказалась груда достаточно тяжёлых камней. Один из детей может взять с собой любой камень, чтобы сделать разность масс на концах качелей допустимой. Помогите друзьям определить минимальную массу камня, благодаря которому они смогут покачаться на качелях.
Формат входных данных
Программа получает на вход три числа A, B, C, записанных в отдельных строках, — массы друзей. В четвёртой строке записано число D — наибольшая допустимая разница масс на концах качелей. Все числа — целые, положительные и не превосходящие 109 .
Формат выходных данных
Программа должна вывести одно целое число — минимальную необходимую массу камня, которую нужно добавить на одну из сторон качелей, чтобы друзья смогли покачаться на них, сев оптимально. Если камень им не понадобится, программа должна вывести число 0.
Замечание
В первом примере Аня и Саша сядут на одну сторону, их суммарная масса будет равна 65 кг. На другую сторону сядет Боря, взяв 15-килограммовый камень, тогда масса Бори с камнем составит 55 кг. Разница весов на концах качелей примет значение 10 кг. Во втором примере Аня и Боря сядут на одну сторону (50 кг), Саша — на другую сторону (45 кг). Разница весов будет равна 5 кг, поэтому камень не понадобится.
| |
![]()
|
262/
80
|
|
Темы:
Структуры данных
Вывод формулы
Комбинаторика
Для последовательности целых чисел \(a_1, a_2, \ldots, a_n\) и целого числа \(x\) обозначим через \(f(a, x)\) количество таких целых \(i\) от \(1\) до \(n\), что \(a_i \le x\).
Для пары последовательностей целых чисел \(a_1, a_2, \ldots, a_n\) и \(b_1, b_2, \ldots, b_n\) обозначим через \(g(a, b, c)\) сумму значений \(|f(a, x)-f(b, x)|\) по всем целым \(x\), лежащим в отрезке \([0, c]\). Более формально, \(g(a, b, c) = \sum_{x=0}^c |f(a, x)-f(b, x)|\).
Вам даны два целых числа \(n\) и \(c\), а также две последовательности целых чисел \(a_1, a_2, \ldots, a_n\) и \(b_1, b_2, \ldots, b_n\), все элементы которых лежат в отрезке \([-1, c]\). Известно, что ни в \(a\), ни в \(b\) нет двух подряд идущих элементов, равных \(-1\).
Скажем, что пара последовательностей целых чисел \(a_1', a_2', \ldots, a_n'\) и \(b_1', b_2', \ldots, b_n'\), все элементы которых лежат в отрезке \([0, c]\), соответствует шаблону \((a, b)\), если выполняются следующие условия:
-
Для всех \(i\) (\(1 \le i \le n\)), таких, что \(a_i \ne -1\), выполняется \(a_i'=a_i\).
-
Для всех \(i\) (\(1 \le i \le n\)), таких, что \(b_i \ne -1\), выполняется \(b_i'=b_i\).
-
Для всех \(i\) (\(1 \le i \le n-1\)) выполняется \(a_i' \le a_{i+1}'\).
-
Для всех \(i\) (\(1 \le i \le n-1\)) выполняется \(b_i' \le b_{i+1}'\).
Обозначим через \(h(a, b, c)\) сумму значений \(g(a', b', c)\) по всем парам последовательностей \((a', b')\), соответствующих шаблону \((a, b)\). Вы должны посчитать \(h(a, b, c)\). Также вы должны обработать \(q\) запросов изменения последовательностей \(a\) и \(b\) и посчитать \(h(a, b, c)\) после каждого изменения. Обратите внимание, что ни в \(a\), ни в \(b\) нет двух подряд идущих элементов, равных \(-1\), ни до всех запросов, ни после какого-либо запроса.
Формат входных данных
Первая строка содержит три целых числа \(n\), \(c\) и \(q\) (\(1 \le n \le 100\,000\), \(0 \le c \le 10^9\), \(0 \le q \le 100\,000\)) — длина последовательностей \(a\) и \(b\), ограничение на значения элементов \(a\) и \(b\) и количество запросов, соответственно.
Вторая строка содержит \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(-1 \le a_i \le c\)) — последовательность \(a\).
Третья строка содержит \(n\) целых чисел \(b_1, b_2, \ldots, b_n\) (\(-1 \le b_i \le c\)) — последовательность \(b\).
В следующих \(q\) строках заданы запросы изменения. Каждый запрос задается тройкой целых чисел \(t\), \(p\), \(x\) (\(1 \le t \le 2\), \(1 \le p \le n\), \(-1 \le x \le c\)). Если \(t=1\), то данный запрос меняет \(a_p\) на \(x\). Если \(t=2\), то данный запрос меняет \(b_p\) на \(x\).
Гарантируется, что до всех изменений и после каждого изменения ни в \(a\), ни в \(b\) нет двух подряд идущих элементов, равных \(-1\).
Формат выходных данных
Выведите \((q+1)\) строку. В \((i+1)\)-й строке (\(0 \le i \le q\)) выведите одно целое число — значение \(h(a, b, c)\) по модулю \(10^9+7\) после применения первых \(i\) запросов изменения.
Примечание
Рассмотрим первый тест из примера. В нем \(n=3\), \(c=4\), \(q=3\). До всех запросов \(a=[-1, 1, 3]\), \(b=[1, -1, 2]\). Шаблону \((a, b)\) соответствуют следующие пары последовательностей:
-
\(a'=[0, 1, 3], b'=[1, 1, 2]\), \(g(a, b, 4)=2\).
-
\(a'=[0, 1, 3], b'=[1, 2, 2]\), \(g(a, b, 4)=3\).
-
\(a'=[1, 1, 3], b'=[1, 1, 2]\), \(g(a, b, 4)=1\).
-
\(a'=[1, 1, 3], b'=[1, 2, 2]\), \(g(a, b, 4)=2\).
Таким образом, ответ на задачу до всех запросов равен \(h(a, b, 4)=2+3+1+2=8\).
В первом запросе \(t=1\), \(p=1\), \(x=2\). Этот запрос меняет \(a_1\) с \(-1\) на \(2\). Таким образом, после этого запроса \(a=[2, 1, 3]\), \(b=[1, -1, 2]\). В последовательности \(a\) нет \(-1\), поэтому в любой паре последовательностей \((a', b')\), соответствующей шаблону \((a, b)\), последовательность \(a'\) должна совпадать с \(a\). В последовательности \(a\) не выполняется условие \(a_1 \le a_2\), поэтому не существует ни одной пары последовательностей, соответствующей шаблону, а тогда \(h(a, b, 4)=0\) после первого запроса.
| |
![]()
|
2/
2
|
|
Темы:
Вывод формулы
В левом-нижнем углу квадратной клетчатой доски размером \(n\times m\) стоит \(k\)-кузнечик. За один ход \(k\)-кузнечик перемещается по доске вправо, вверх или вправо-вверх по диагонали не более чем на \(k\) клеток.
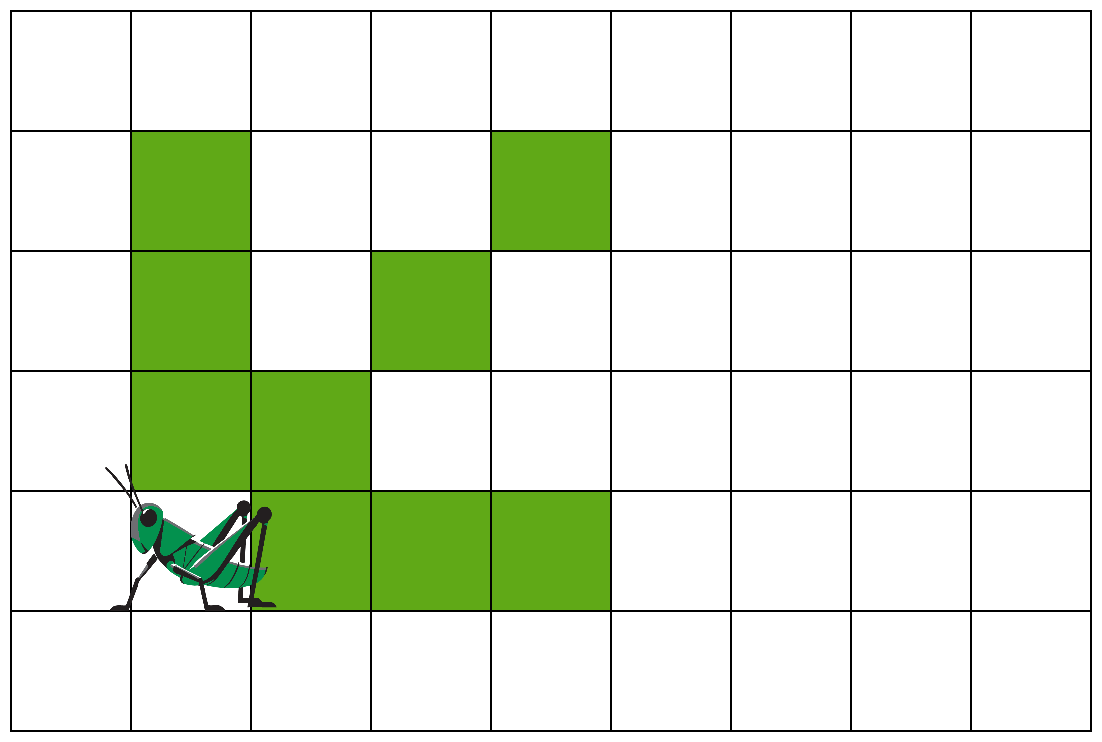
Возможные ходы \(k\)-кузнечика для \(k = 3\).
Необходимо передвинуть \(k\)-кузнечика в правый верхний угол доски в клетку \((n, m)\). За какое минимальное число ходов можно передвинуть \(k\)-кузнечика из клетки \((1, 1)\) в клетку \((n, m)\)?
Формат входных данных
В первой строке заданы три целых числа \(n\), \(m\) и \(k\) — размеры сторон доски и максимальное число клеток, на которое может ходить \(k\)-кузнечик, соответственно (\(1 \le n, m, k \le 10^9\)).
Формат выходных данных
Выведите одно число — минимальное число ходов, необходимое, чтобы передвинуть \(k\)-кузнечика из клетки \((1, 1)\) в клетку \((n, m)\).
| |
![]()
|
51/
24
|
|
Темы:
Динамическое программирование
Вывод формулы
Комбинаторика
Будем назвать натуральное число интересным, если в его десятичной записи первая цифра совпадает с последней.
Дано число \(n\). Найдите количество интересных чисел, не превышающих \(n\).
Формат входных данных
На ввод подается целое число \(n\) (\(1 \le n \le 10^{18}\)).
Обратите внимание, что для считывания этого числа вам может понадобиться 64-битный тип данных (<<long long>> в C++, <<long>> в Java, <<int64>> в Паскале).
Формат выходных данных
Выведите одно целое число — количество интересных натуральных чисел, не превышающих \(n\).
| |
![]()
|
48/
11
|
|
Темы:
Циклы
Вывод формулы
 Мумми-мама решила испечь печенье к празднику. Она печет по Мумми-мама решила испечь печенье к празднику. Она печет по B печений за один раз, и печёт их в следующие моменты времени: A минут, 2A минут, 3A минут и каждое последующее число, кратное A минутам после начала выпечки. Определите, сколько печений будет испечено Мумми-мамой к празднику, который наступит через T+0,5 после начала выпечки.
Формат входных данных
Программа получает на вход одну строку, содержащую три числа A, B и T. 1 <= A, B, T <= 20, A <= T. Все числа целые положительные.
Формат выходных данных
Выведите одно число - ответ на задачу.
| |
![]()
|
1614/
550
|
|
Темы:
Перебор с отсечением
Дата и время
Вывод формулы
Парламент некоторой страны принял новый закон о праздничных днях. Согласно этому закону первые K дней года, а также 23 февраля (День олимпиады по информатике) и 8 марта объявляются праздничными, а все остальные праздники отменяются. При этом все выходные (суббота и воскресенье), попавшие на праздничные дни, переносятся на следующие за этими праздниками рабочие дни.
В зависимости от того, на какой день недели приходится 1 января, количество нерабочих дней, которые идут подряд, может меняться.
Требуется определить, какое наибольшее количество нерабочих дней может идти подряд.
Входные данные
На вход подается единственное число K (1≤K≤50).
Выходные данные
Требуется вывести единственное число — наибольшее количество нерабочих дней, идущих подряд.
| |
![]()
|
6/
1
|
|
Темы:
Вывод формулы
Том Сойер получил важное задание по покраске забора. Забор состоит из n досок. Он когда-то был покрашен, однако с некоторых участков забора краска облупилась. Эти доски Тому и необходимо покрасить. Так как забор большой, пришлось подвезти к забору целую цистерну с краской. Цистерна была помещена у края забора и не может перемещаться. У Тома есть ведерко, набрав краски в которое, Том может покрасить k
досок забора. При этом Том может в любой момент вернуться за краской к цистерне.
Изначально Том находится у цистерны. Соседние доски находятся на расстоянии 1 фута друг от друга, цистерна находится на расстоянии 1 фута от первой доски. По окончании работы Том должен положить кисточку и ведерко на свою исходную позицию рядом с цистерной.
Требуется выяснить, какое минимальное расстояние Тому необходимо пройти, чтобы покрасить забор.
Входные данные
Первая строка содержит количество досок в заборе n (1 ≤ n ≤ 109) и вместимость ведерка k (1 ≤ k ≤ 100). Во второй строке содержится количество неокрашенных отрезков забора m (1 ≤ m ≤ 50).
Далее следуют m строк, в каждой из которых описан один неокрашенный отрезок. Отрезок описывается своей левой границей li и правой границей ri (1 ≤ li ≤ ri ≤ n). Такое описание означает, что не покрашены li-я, (li+1)-я, …, (ri–1)-я, ri-я доски забора (доски нумеруются от 1 до n). Гарантируется, что неокрашенные отрезки, заданные во входном файле, не пересекаются.
Выходные данные
Выведите одно число — минимальное расстояние в футах, которое необходимо пройти Тому для выполнения своего ответственного задания.

| |
![]()
|
5/
1
|
|
Темы:
Цикл for
Вывод формулы
Возьмем кубик и приклеим к его граням еще по такому же кубику. В результате получим фигуру, представленную на втором рисунке. К свободным граням полученной фигуры, приклеим еще кубики. На рисунке представлены "кубооктаэдры" степеней 0, 1, 2.
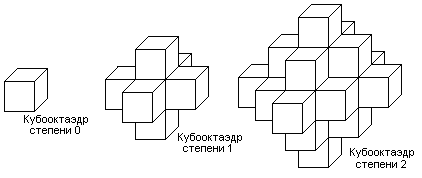
Кубооктаэдром степени N назовем фигуру, полученную в результате N-го доклеивания кубиков. Составить программу, подсчитывающую, количество кубиков для кубооктаэдра N-й степени.
Входные данные
Содержит единственное число - степень кубооктаэдра 0 <= N <= 100000
Выходные данные
Вывести одно число - количество кубиков для кубооктаэдра степени N.
| |
![]()
|
82/
12
|
|
Темы:
Вывод формулы
В знаменитом магазине <<Двоечка>> продукты продаются всего два дня в неделю — понедельник и вторник — причём в разные дни по разным ценам. Вы захотели купить \(n\) килограммов картофеля на неделю. По понедельникам один килограмм картофеля стоит \(a\) рублей, а по вторникам — \(b\) рублей. Чтобы упростить работу кассирам, в <<Двоечке>> можно покупать только целое число килограммов.
Вам крупно повезло, ведь в <<Двоечке>> проходит акция: каждый понедельник за каждые \(m\) килограммов купленного картофеля дарят ещё один!
Найдите минимальную сумму, за которую можно приобрести хотя бы \(n\) килограммов картофеля на неделю.
Формат входных данных
В первой строке вводится целое число \(a\) \((1 \leqslant a \leqslant 10^9)\) — цена одного килограмма картофеля в понедельник.
Во второй строке вводится целое число \(b\) \((1 \leqslant b \leqslant 10^9)\) — цена одного килограмма картофеля во вторник.
В третьей строке вводится целое число \(n\) \((\mathbf{1 \leqslant n \leqslant 10^6})\) — желаемое количество килограммов картофеля.
В четвертой строке вводится целое число \(m\) \((1 \leqslant m \leqslant 10^6)\) — количество килограммов картофеля, участвующее в акции.
Формат входных данных
Выведите одно целое число — минимальное число рублей, которое придется заплатить, чтобы купить хотя бы \(n\) килограммов картофеля.
Обратите внимание, что ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать и с типом int.
Примечание
В первом примере выгодно купить один килограмм в понедельник за 5 рублей, получить еще один килограм в подарок и купить килограмм во вторник за 4 рубля. Купить три килограмма дешевле не получится.
Во втором примере выгодно купить три килограмма в понедельник и получить один килограмм в подарок.
В третьем примере акцией пользоваться невыгодно.
В четвертом примере выгодно купить шесть килограммов в понедельник, получить по акции три килограмма и купить еще один килограмм во вторник.
| |
![]()
|
6/
5
|
|
Темы:
Вывод формулы
В знаменитом магазине <<Двоечка>> продукты продаются всего два дня в неделю — понедельник и вторник — причём в разные дни по разным ценам. Вы захотели купить \(n\) килограммов картофеля на неделю. По понедельникам один килограмм картофеля стоит \(a\) рублей, а по вторникам — \(b\) рублей. Чтобы упростить работу кассирам, в <<Двоечке>> можно покупать только целое число килограммов.
Вам крупно повезло, ведь в <<Двоечке>> проходит акция: каждый понедельник за каждые \(m\) килограммов купленного картофеля дарят ещё один!
Найдите минимальную сумму, за которую можно приобрести хотя бы \(n\) килограммов картофеля на неделю.
Формат входных данных
В первой строке вводится целое число \(a\) \((1 \leqslant a \leqslant 10^9)\) — цена одного килограмма картофеля в понедельник.
Во второй строке вводится целое число \(b\) \((1 \leqslant b \leqslant 10^9)\) — цена одного килограмма картофеля во вторник.
В третьей строке вводится целое число \(n\) \((1 \leqslant n \leqslant 10^9)\) — желаемое количество килограммов картофеля.
В четвертой строке вводится целое число \(m\) \((1 \leqslant m \leqslant 10^9)\) — количество килограммов картофеля, участвующее в акции.
Формат выходных данных
Выведите одно целое число — минимальное число рублей, которое придется заплатить, чтобы купить хотя бы \(n\) килограммов картофеля.
Обратите внимание, что ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать и с типом int.
Примечание
В первом примере выгодно купить один килограмм в понедельник за 5 рублей, получить еще один килограм в подарок и купить килограмм во вторник за 4 рубля. Купить три килограмма дешевле не получится.
Во втором примере выгодно купить три килограмма в понедельник и получить один килограмм в подарок.
В третьем примере акцией пользоваться невыгодно.
В четвертом примере выгодно купить шесть килограммов в понедельник, получить по акции три килограмма и купить еще один килограмм во вторник.
| |
![]()
|
28/
9
|
|
Темы:
Вывод формулы
Для МОШ по информатике было придумано и подготовлено \(n\) задач. Всего в олимпиаде будут учавствовать \(k\) школьников. И вот до олимпиады осталась всего неделя! Но, как вы знаете, некий <<Турист>> очень любит придумывать задачи и потом давать их на разные олимпиады. А так как <<Турист>> ну уж очень умный, то он явно придумает и даст все задачи, которые придумало жюри МОШа. В рамках подготовки к олимпиаде, школьники будет решать задачи <<Туриста>>. Причём вы знаете, что каждый из участников прорешает за неделю не менее \(a\) и не более \(b\) задач из тех, что собираются дать на МОШ. Жюри даст на олимпиаду все задачи, которые не решал никто из участников ранее. Скажите минимальное и максимальное количество задач, которые могут быть даны на МОШ из заранее подготовленных.
Формат входных данных
В первой строке вводится число \(n\) \((1 \leqslant n \leqslant 10^9)\) — количество задач, подготовленных для МОШ по информатике.
Во второй строке вводится число \(k\) \((1 \leqslant k \leqslant 10^9)\) — число участников МОШ.
В третьей строке вводится число \(a\) \((1 \leqslant a \leqslant n)\) — минимальное число задач, которое прорешает каждый из участников в течение недели.
В третьей строке вводится число \(b\) \((a \leqslant b \leqslant n)\) — максимальное число задач, которое может прорешать каждый из участников в течение недели.
Формат выходных данных
Выведите два числа – минимальное и максимальное число задач, которые жюри может дать на МОШ.
| |
![]()
|
65/
13
|
|
Темы:
Вывод формулы
В известной школе прошёл урок физкультуры. Как полагается, всех построили в шеренгу и попросили рассчитаться на <<первый–\(k\)-й>>.
Как известно, расчёт на <<первый–\(k\)-й>> происходит следующим образом: первые \(k\) человек имеют номера \(1, 2, 3, \ldots, k\), следующие \(k - 1\) человек имеют номера \(k - 1, k - 2, \ldots, 1\), следующие \(k - 1\) человек имеют номера \(2, 3, \ldots, k\) и т.д. Таким образом, расчёт повторяется через каждые \(2k - 2\) позиции. Примеры расчёта приведены в разделе <<Замечание>>.
Мальчик Вася постоянно всё забывает. Например, он забыл позицию, которую занимал в шеренге. Но он помнит число \(k\), описанное выше, номер, который он получил при расчёте, а также, что его позиция в шеренге была не больше \(n\). Другими словами, если Вася стоял на позиции \(y\) в шеренге, то \(y \leq n\). Помогите Васе понять, сколько есть различных позиций в ряду, где он мог стоять.
Формат входных данных
Первая строка содержит одно целое число \(k\) (\(2 \leq k \leq 10^9\)) — характеристика расчёта, описанная в условии.
Вторая строка содержит одно целое число \(x\) (\(1 \leq x \leq k\)) — номер, который Вася получил при расчёте.
Третья строка содержит одно целое число \(n\) (\(x \leq n \leq 10^9\)) — верхнее ограничение на позицию Васи.
Формат выходных данных
Выведите единственное целое число – количество различных позиций, которые подходят под данные ограничения.
Замечание
В первом примере подходят позиции равные \(2, 4, 6, 8, 10\).
Во втором примере подходят позиции равные \(2, 4, 6, 8, 10\).
В третьем примере подходят позиции равные \(3\) и \(7\).
Пример расчёта для \(k = 2\), \(k = 3\) и \(k = 5\):
| \(2\) |
\(1\) |
\(2\) |
\(1\) |
\(2\) |
\(1\) |
\(2\) |
\(1\) |
\(2\) |
\(1\) |
\(2\) |
| \(3\) |
\(1\) |
\(2\) |
\(3\) |
\(2\) |
\(1\) |
\(2\) |
\(3\) |
\(2\) |
\(1\) |
\(2\) |
| \(5\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(4\) |
\(3\) |
\(2\) |
\(1\) |
\(2\) |
| |
![]()
|
19/
5
|
|
Темы:
Вывод формулы
У Пети есть прямоугольник размера \(a \times b\) с целыми сторонами, хотя бы одна из которых больше \(1\). Он пробует разрезать этот прямоугольник на два прямоугольника с целыми сторонами, сделав разрез, параллельный какой-то из сторон исходного прямоугольника. Затем Петя пытается из двух получившихся прямоугольников сложить какой-то отличный от исходного прямоугольник, при этом он может как угодно поворачивать и двигать эти два прямоугольника. Если у него получается это сделать, то он называет прямоугольник \(a \times b\) интересным.
Обратите внимание, что если два прямоугольника отличаются поворотом на \(90^{\circ}\), то они считаются одинаковыми. Например, прямоугольники \(6 \times 4\) и \(4 \times 6\) считаются одинаковыми.
Таким образом, прямоугольник \(2 \times 6\) является интересным, потому что его можно разрезать на два прямоугольника \(2 \times 3\), после чего из этих двух прямоугольников сложить прямоугольник \(4 \times 3\), который отличается от прямоугольника \(2 \times 6\).
При этом прямоугольник \(2 \times 1\) не является интересным, потому что его можно разрезать только на два прямоугольника \(1 \times 1\), а из них можно сложить только прямоугольники \(1 \times 2\) и \(2 \times 1\), которые считаются одинаковыми с исходным.
Также у Пети есть некоторое целое число \(n\). Он хочет узнать, сколько существует различных интересных прямоугольников со сторонами, которые являются целыми числами, не превосходящими \(n\). Помогите ему это сделать.
Формат входных данных
Первая и единственная строка содержит одно целое число \(n\) (\(2 \le n \le 2 \cdot 10^9\)) — ограничение на длину сторон прямоугольника.
Формат выходных данных
Выведите одно целое число — количество различных интересных прямоугольников с длинами сторон, не превышающими \(n\).
Обратите внимание, что ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать.
Замечание
В первом примере только прямоугольник \(2 \times 2\) является интересным: его можно разрезать на два прямоугольника \(1 \times 2\), а из них можно сложить прямоугольник \(1 \times 4\). Обратите внимание, что прямоугольник \(1 \times 1\) не является интересным, потому что хотя бы одна сторона должна быть больше \(1\).
Во втором примере прямоугольники \(2 \times 2\) и \(2 \times 3\) являются интересными. Прямоугольник \(2 \times 3\) можно разрезать на два прямоугольника \(1 \times 3\), а из них можно сложить прямоугольник \(1 \times 6\). Прямоугольник \(3 \times 3\) не является интересным, потому что его можно разрезать только на два прямоугольника \(1 \times 3\) и \(2 \times 3\), но из них можно сложить только прямоугольник \(3 \times 3\). Обратите внимание, что прямоугольники \(2 \times 3\) и \(3 \times 2\) считаются одинаковыми, поэтому в ответе их нужно учесть только один раз.
| |
![]()
|
27/
9
|
|
Темы:
Вывод формулы
В самом лучшем университете России есть специальный предмет, который называется <<Теория Лени>>. Вы очень любите этот предмет и стараетесь постоянно использовать то, чему вас там научили.
Но, как и везде, на нём есть устный экзамен. Всего есть \(n\) билетов, из которых вы выучили ровно \(a\) (ваша лень не позволяет вам выучить больше).
Экзамен проходит в стандартном формате: есть стопка с билетами, каждый билет встречается в ней ровно один раз, и каждый студент случайно выбирает себе один билет. При этом, когда студент достал билет, то он забирает его себе и не возвращает обратно в стопку.
Вы знаете, что до вас отвечали уже \(b\) человек, а это значит, что стопка содержит уже на \(b\) билетов меньше. Так как вас интересует не только <<Теория Лени>>, но и математика (и даже чуть-чуть информатика!), вы хотите узнать, какое минимальное и максимальное количество билетов из оставшихся вы можете знать.
Формат входных данных
Первая строка содержит одно целое число \(n\) (\(1 \leq n \leq 10^9\)) — количество билетов на экзамене.
Вторая строка содержит одно целое число \(a\) (\(1 \leq a \leq n\)) — количество билетов, которые вы выучили.
Третья строка содержит одно целое число \(b\) (\(0 \leq b < n\)) — количество людей, которые уже взяли свой билет до вас.
Формат выходных данных
Вывод вашей программы должен состоять из двух строк.
Первая строка должна содержать единственное целое число — минимальное количество билетов, которое вы можете знать из оставшихся.
Вторая строка должна содержать единственное целое число — максимальное количество билетов, которое вы можете знать из оставшихся.
В первом примере давайте считать, что вы знаете билеты с номерами \(1, 2, 3, 4\). Тогда, если люди до вас вытянули билеты с номерами \(1, 2, 3\), то остался только \(1\) билет, который вы знаете. А если люди до вас вытянули билеты с номерами \(4, 5, 6\), то вы знаете \(3\) билета из оставшихся.
| |
![]()
|
53/
16
|
|
Темы:
Вывод формулы
Пётр любит шахматы и математику. Он знает, что самая мощная фигура в шахматах - это ферзь, потому что он ходит и как ладья, на все клетки на одной с ним вертикали или горизонтали, и как слон, на все клетки по диагоналям. Ферзя можно поставить на доску 8 X 8 так, чтобы он контролировал (то есть мог переместиться в эти клетки за один ход) целых 27 клеток доски!
Петра заинтересовало, какое максимальное количество клеток может контролировать ферзь на прямоугольных досках самых разных размеров. Помогите ему в решении этой задачи.
Формат входных данных
Первая строка входных данных содержит целое число n (1 ≤ n ≤ 109) - размер доски по вертикали.
Вторая строка входных данных содержит целое число m (1 ≤ m ≤ 109) - размер доски по горизонтали.
Формат выходных данных
Программа должна вывести одно целое число - максимальное количество клеток, которое может контролировать ферзь на доске n x m.
Обратите внимание на то, что ответ в этой задаче может превышать возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип long long в языке C++, тип int64 в Pascal, тип long в Java и C#).
Замечание
Второй пример из условия приведён на рисунке. Крестиками обозначены клетки, которые контролирует ферзь.
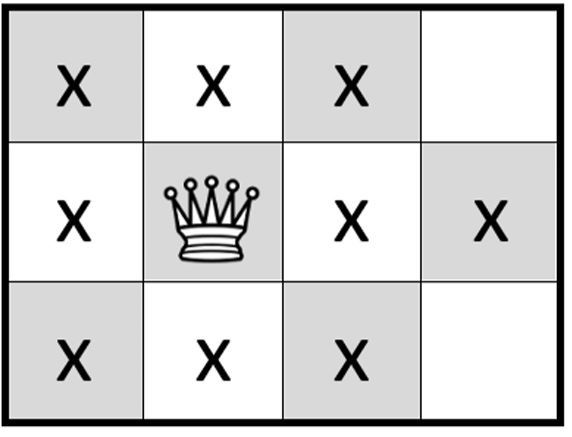
| |
![]()
|
315/
75
|
|
Темы:
Целые числа
Вывод формулы
Обувная фабрика собирается начать выпуск элитной модели ботинок. Дырочки для шнуровки будут расположены в два ряда, расстояние между рядами равно a, а расстояние между дырочками в ряду b. Количество дырочек в каждом ряду равно N. Шнуровка должна происходить элитным способом “наверх, по горизонтали в другой ряд, наверх, по горизонтали и т.д.” (см. рисунок). Кроме того, чтобы шнурки можно было завязать элитным бантиком, длина свободного конца шнурка должна быть l. Какова должна быть длина шнурка для этих ботинок?
Запрещено использовать операторы if, while, for, repeat-until (Паскаль)
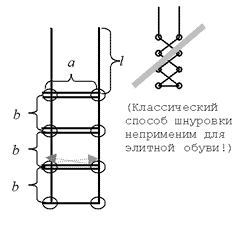
Входные данные: Программа получает на вход четыре натуральных числа a, b, l и N.
Выходные данные: Программа должна выводить одно число – искомую длину шнурка.
Примеры
входные данные
2
1
3
4
выходные данные
26
| |
![]()
|
156/
48
|
|
Темы:
Целые числа
Бинарный поиск по ответу
Вывод формулы
Медведь Василий собирает ягоды. Он будет счастлив, если ягод малины в его корзинке окажется не менее трети от общего числа ягод. Медведь Василий уже собрал N ягод, из них K штук малины. Василий уже изрядно устал собирать ягоды, поэтому помогите ему понять, какое минимальное число ягод малины ему необходимо собрать, чтобы быть счастливым.
Входные данные
Программа получает на вход два целых числа N и K (N > 0, 0 ≤ K ≤ N, K<=109, N<=2*109), записанные в отдельных строках, — текущее количество ягод в корзинке медведя Василия и количество ягод малины в корзинке.
Выходные данные
Выведите единственное число — минимальное число ягод малины, которое необходимо собрать.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
27
7 |
3 |
В примере всего ягод в корзинке 27, из которых малины 7 ягод.
Если в собрать ещё 3 ягоды малины, то в корзинке станет 30 ягод, из которых малины будет 10. |
| |
![]()
|
650/
52
|
|
Темы:
Вывод формулы
Магистр Максимус со своим верным другом фокусником Феликсом играют в игру камушки. Правила этой игры описаны ниже.
- Вначале на столе лежит куча камней.
- Ходы Максимуса и Феликса чередуются по очереди, причем Максимус всегда ходит первым.
- На каждом ходу тот, чья очередь подошла, убирает от 1 до 3 камней из кучи.
- Побеждает тот, кто уберет последний камень.
Учитывая n - количество камней в куче, верните имя того, кто победит в игре, при условии, что и Максимус, и Феликс всегда играют оптимально.
Входные данные
Программа получает на вход натуральное число n - количество камней в куче (1<= n <= 231 - 1).
Выходные данные
Выведите одну из английских букв: M, если победит в игре Максимус и F - если победит Феликс.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
F |
| 2 |
2 |
M |
| |
![]()
|
173/
50
|
|
Темы:
Условный оператор
Вывод формулы
На стройку многоэтажного дома завезли инструменты. Прорабу необходимо доставить инструменты с этажа A на этаж B. Для вызова подъемника на всех этажах строящегося здания, кроме первого и последнего, есть две кнопки. Кнопка вниз перемещает подъемник вниз, кнока вверх - перемещает вверх. Когда прораб нажал нужную кнопку, подъемник находился на этаже С и вез груз на этаж D. Работает подъемник следующим образом:
- если подъемник проезжает мимо этажа, на котором нажата кнопка вызова, и, при этом, движется в подходящем направлении, то подъемник останавливается и в него можно зайти.
Подъемник перемещается между соседними этажами за одну единицу времени, также одну единицу времени занимает остановка подъемника на этаже для загрузки или разгрузки.
Определите сколько времени необходимо прорабу, чтобы доставить инструменты до этажа B, при условии, что никто больше не будет вызывать подъемник.
Входные данные
Первая строка ввода содержит четыре целых числа A, B, C и D, разделенных одним пробелом (1 <= A, B, C, D <= 20, A≠B, C≠D, A≠C).
Выходные данные
Вывести одно целое число – количество единиц времени, которое пройдет с момента вызова подъемника до момента, когда инструменты разгрузят из подъемника на этаже B.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 9 2 5 |
10 |
| 2 |
3 9 5 2 |
13 |
Примечание
Пояснение к примеру 1
Подъемник за 1 единицу времени доедет до 3-го этажа, остановится на 1 единицу времени, чтобы прораб смог погрузить инструменты на подъемник, затем через 2 единицы времени доедет до 5-го этажа и остановится на 1 единицу времени для разгрузки груза, через 4 единицы времени подъемник довезет инструменты до 9-го этажа, и через 1 единицу времени инструменты рагрузят.
| |
![]()
|
19/
0
|
|
Темы:
Целые числа
Вывод формулы
По одну сторону улицы находятся дома с нечётными номерами (1, 3, 5, …), по другую сторону – с чётными (2, 4, 6, …). Дом № 1 находится напротив дома № 2, дом № 3 – напротив дома № 4 и т. д. До соседнего дома нужно идти вдоль по улице одну минуту, неважно, с какой стороны улицы он находится (то есть от дома № 1 нужно идти одну минуту как до дома № 3, так и до дома № 4). До дома, стоящего напротив, идти не нужно.
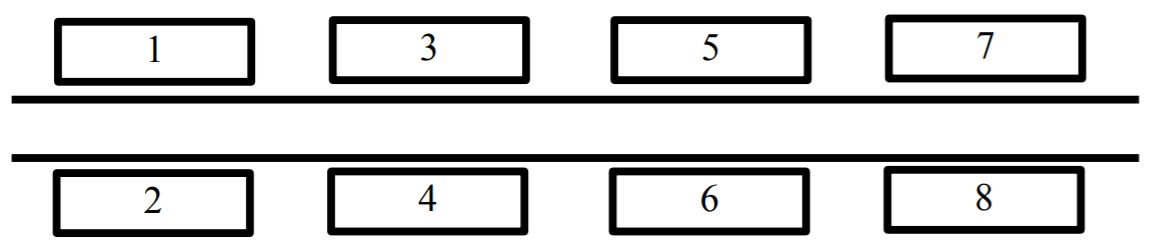
Громозека вышел на улицу из дома номер A и должен дойти до дома номер B. Определите, сколько минут ему нужно идти вдоль по улице.
Запрещено использовать какие-либо алгоритмические конструкции для решения данной задачи. Можно использовать только арифметические операции (без использования встроенных функций).
Входные данные
Программа получает на вход два различных целых положительных числа A и B,не превосходящие 2×109, – номера домов.
Выходные данные
Программа должна вывести одно число – искомое количество минут.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
8 |
3 |
| |
![]()
|
347/
48
|
|