| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
"Два указателя"
В зале есть ряд из n мест, пронумерованных числами от 1 до n слева направо. Пройти к любому месту можно либо с левого конца ряда, либо с правого. Первоначально некоторые места уже заняты и ещё k человек по одному садятся на свободные места. Каждый человек выбирает себе свободное место, до которого ближе всего идти от одного из концов ряда. Если же есть два свободных места, одинаково удалённых от левого и правого концов ряда, то человек выберет левое место (с меньшим номером).
Определите номера мест, которые будут выбирать люди, в порядке их прихода.
Формат входных данных
Первая строка входных данных содержит целое число n (1 ≤ n ≤ 2 · 105 ) — количество мест в ряду.
Вторая строка содержит целое число k (1 ≤ k ≤ n) — количество приходящих людей.
Третья строка содержит строку s длины n, состоящую из символов «0» и «1» и задающую первоначальную рассадку. Занятые места обозначаются единицами, пустые — нулями. Гарантируется, что в строке s содержится не менее k нулей.
Формат выходных данных
Программа должна вывести k чисел — номера выбранных мест в порядке прихода новых людей.
Замечание
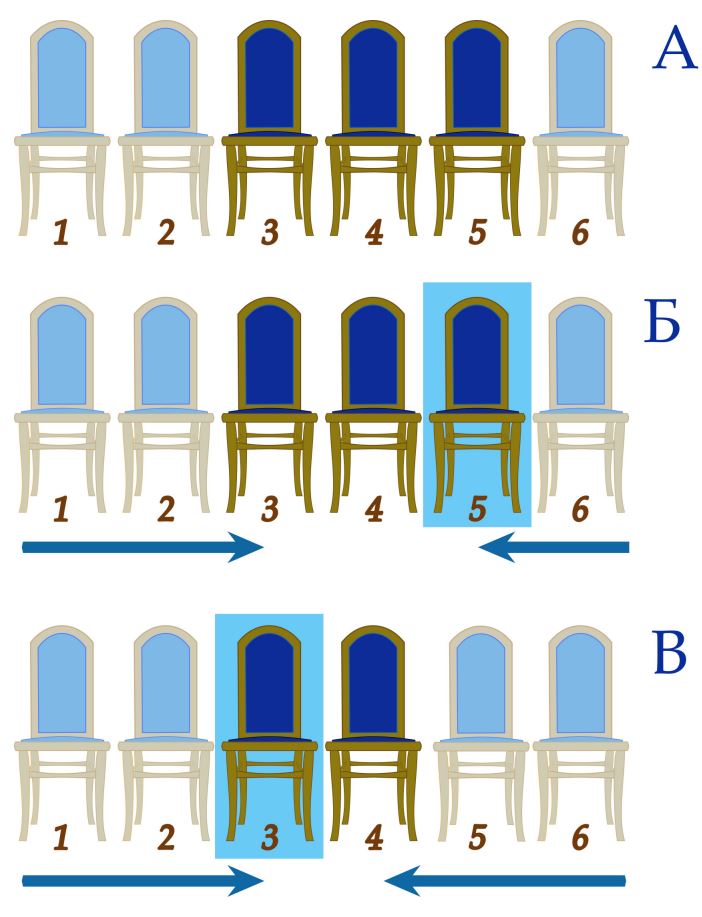
В первом примере первоначально заняты места 1, 2 и 6 (рисунок А).
Если первый пришедший будет двигаться с левой стороны ряда, он пройдёт мимо 1 и 2 места, прежде чем доберётся до свободного места с номером 3. Если же он будет двигаться с правой стороны ряда, то ему понадобится пройти мимо одного места с номером 6, после чего он сможет занять место 5. Именно это место он и выберет (рисунок Б).
Второй пришедший может занять либо место с номером 3, двигаясь с левой стороны и проходя мимо двух занятых мест 1 и 2, либо место с номером 4, двигаясь с правой стороны и проходя мимо двух занятых мест 6 и 5. Поскольку в обоих случаях ему нужно пройти мимо двух занятых мест, он будет двигаться с левой стороны и займёт место с номером 3.
Во втором примере в ряду 6 мест, второе и пятое места изначально уже заняты, заходят ещё 3 человека. Первый заходящий человек будет выбирать между первым и шестым местами, заходя с левого или правого края соответственно. В обоих случаях ему придётся пройти мимо нуля занятых мест, поэтому он решит зайти слева и сесть на 1 место. Второй человек будет выбирать между третьим и шестым местами. В первом случае ему придётся идти мимо двух занятых мест, во втором — мимо нуля, поэтому он выберет зайти справа — 6 место. Третий человек будет выбирать между третьим и четвертым местами. В обоих случаях ему придётся пройти мимо двух занятых мест, поэтому он выберет зайти слева — 3 место.
| |
![]()
|
27/
8
|
|
Темы:
"Два указателя"
Префиксные суммы(минимумы, ...)
Рассмотрим отрезок целых неотрицательных чисел от \(l\) до \(r\). Запишем их подряд в десятичной системе счисления, получив строку \(a\). Например, если \(l=3\), \(r=10\), то \(a=345678910\).
Найдите такой отрезок подряд идущих неотрицательных чисел \([l,r]\) (\(0 \le l \le r \le 10^{18}\)), что записанная для него строка \(a\) имеет длину ровно \(S\), а количество чисел на отрезке \([l,r]\) максимально.
Формат входных данных
Первая строка содержит одно целое число \(S\) (\(1 \le S \le 10^{18}\)).
Формат выходных данных
В первой строке выведите длину отрезка \([l,r]\). Если решения не существует, выведите одно целое число \(-1\).
Если решение существует, во второй строке выведите искомые границы отрезка \(l\) и \(r\).
Если существуют несколько решений, выведите любое из них.
| |
![]()
|
1/
1
|
|
Темы:
Множества
"Два указателя"
Разреженные таблицы (sparse table)
Алексей, возможно, самый умный и при этом самый ленивый человек в мире. Сегодня он участвует в олимпиаде.
На олимпиаде участникам даны \(n\) задач, за правильное решение \(i\)-й задачи, участник получит \(a_i\) баллов, за неправильное решение баллов не дают. Дипломы призера дадут тем участникам, которые наберут хотя бы половину от суммарного числа баллов. Например, если на олимпиаде дано три задачи, стоимости которых в баллах равны \(1\), \(3\) и \(4\), соответственно, для получения диплома призера достаточно набрать четыре балла.
Алексей пришел на олимпиаду с целью получить диплом призера. При этом Алексей очень умен и может правильно решить любую задачу на олимпиаде. Но в то же время Алексей очень ленив и хочет решить как можно меньше задач.
Алексей настолько ленив, что даже задачи, которые он будет решать, выбирает лениво. Он хочет выбрать некоторую задачу с номером \(k\), а затем решать задачи с номерами \(k, k+1, k+2 \ldots\) до тех пор, пока ему не будет хватать баллов на диплом призера. Максимум, на что готов Алексей, это пропустить одну задачу и не решать ее, чтобы решить в итоге еще меньше задач.
Зная стратегию Алексея и информацию о задачах олимпиады, определите минимальное количество задач, которые нужно решить Алексею, чтобы получить диплом призера.
Формат входных данных
В первой строке дано одно натуральное число \(n\) — количество задач на олимпиаде (\(1 \le n \le 10^5\)).
Во второй строке заданы \(n\) чисел \(a_1, a_2, \dots a_n\) — стоимости каждой задачи в баллах (\(1 \le a_i \le 10^9\)).
Формат выходных данных
Выведите одно число — минимальное количество задач, которые может решить Алексей, придерживаясь своей стратегии, чтобы получить диплом призера.
Примечание
В первом тесте из примера для получения диплома призера необходимо набрать хотя бы четыре балла. Алексей может начать решать с третьей задачи, пропустить четвертую и набрать четыре балла, решив две задачи.
Во втором тесте достаточно решить только вторую задачу, набрав три балла.
| |
![]()
|
1/
1
|
|
Темы:
"Два указателя"
Хеш
Будем называть цепочкой слов длины n последовательность слов w1, w2, …, wn, такую, что для всех i от 1 до n – 1 слово wi является собственным префиксом слова wi+1.
Слово u длины k называется собственным префиксом слова v длины l, если l > k и первые k букв слова v совпадают со словом u. Например, «program» является собственным префиксом слова «programmer».
Задано множество слов S = {s1, s2, …, sm} и последовательность чисел x[1], x[2], …, x[k]. Требуется найти такие числа l и r (l ≤ r), что sx[l], sx[l + 1], …, sx[r – 1], sx[r] является цепочкой слов, и количество слов в цепочке (число r – l + 1) максимально.
Входные данные
Первая строка входного файла содержит целое число m (1 ≤ m ≤ 250 000). Каждая из следующих m строк содержит по одному слову из множества S.
Все слова не пусты, имеют длину, не превосходящую 250 000 символов, и состоят только из строчных букв латинского алфавита. Суммарная длина всех слов не превосходит 250 000.
Следующая строка содержит число k (1 ≤ k ≤ 250 000). Последняя строка входного файла содержит k чисел — последовательность чисел x[1], x[2], …, x[k] (для всех i выполнено 1 ≤ x[i] ≤ m).
Выходные данные
Выведите в первой строке выходного файла два числа: l и r. Если оптимальных ответов несколько, выведите любой из них. Разделяйте числа пробелом.
| |
![]()
|
2/
2
|
|
Темы:
"Два указателя"
Жадный алгоритм
Девочка Лена — самая экономная девочка в Москве. Поэтому когда папа поручил ей закупку продуктов для поездки на дачу, она сразу отправилась в самый лучший магазин — <<PriceFixed>>. У этого магазина есть несколько особенностей:
-
В магазине есть бесконечный запас каждого товара.
-
Все товары в нем стоят одинаково — ровно 2 рубля.
-
Для каждого из \(i\) товаров предусмотрена скидка для опытных покупателей: если вы уже приобрели \(b_i\) товаров (любого типа, не обязательно типа \(i\)), то на все последующие покупки \(i\)-го товара будет действовать скидка \(50\%\) (то есть, \(i\)-й товар можно будет покупать за 1 рубль!).
Лене нужно купить \(n\) товаров: \(i\)-го товара нужно купить \(a_i\) штук. Помогите Лене понять, какую минимальную сумму денег ей нужно будет потратить, если она будет выбирать порядок покупки товаров оптимальным образом.
Формат входных данных
В первой строке вводится число \(n\) \((1 \leq n \leq 100\,000)\) — количество различных товаров в списке.
В следующих \(n\) строках вводятся описания товаров. Каждое описание состоит из двух чисел \(a_i\) и \(b_i\), (\(1 \leq a_i \leq 10^{14}\), \(1 \leq b_i \leq 10^{14}\)) — требуемое число товаров типа \(i\) и сколько товаров нужно купить, чтобы получить скидку на товар \(i\).
Сумма всех \(a_i\) в тесте не превосходит \(10^{14}\).
Формат выходных данных
Выведите искомую минимальную сумму, которая требуется Лене для совершения всех покупок.
Примечание
В первом примере из условия Лена может купить товары в таком порядке:
-
единицу товара 3 за 2 рубля,
-
единицу товара 1 за 2 рубля
-
единицу товара 1 за 2 рубля,
-
единицу товара 2 за 1 рубль (она может купить его со скидкой, так как уже куплено 3 товара),
-
единицу товара 1 за 1 рубль (она может купить его со скидкой, так как уже куплено 4 товара).
Суммарно она потратит 8 рублей. Можно показать, что меньше потратить невозможно.
Во втором примере из условия Лена может купить товары в таком порядке:
-
единицу товара 1 за 2 рубля,
-
две единицы товара 2 по 2 рубля за каждую,
-
единицу товара 5 за 2 рубля,
-
единицу товара 3 за 1 рубль,
-
две единицы товара 4 по 1 рублю за каждую,
-
единицу товара 1 за 1 рубль.
Суммарно при таком порядке приобретения товаров Лена потратит 12 рублей.
| |
![]()
|
5/
4
|
Темы:
"Два указателя"
Два сотрудника одной известной компании Алиса и Боб предложили тимлиду два решения возникшего в критическом месте бага. Теперь Алиса подозревает, что сотрудник Боб просто взял ее код и добавил в него не влияющие на функциональность символы, чтобы создать впечатление более интенсивной работы.
Компания пишет на эзотерическом языке программирования, похожем на Malbolge, поэтому код каждого из сотрудников представляет из себя строчку из маленьких латинских букв. Код Алисы — строка \(t\), а код Боба — строка \(s\).
Поскольку клавиатура Боба сломана, он может печатать ровно два символа за раз, то есть может вставлять в любое место строки два любых (не обязательно одинаковых) символа. После заявления Алисы о подозрении Боба в плагиате их начальник начал анализировать строки \(s\) и \(t\), пытаясь понять, мог ли Боб получить строку \(s\) из строки \(t\) со своей сломанной клавиатурой. Для этого он пытается постепенно удалять из строки \(s\) по два соседних символа, пока не получит в итоге строrку \(t\).
Помогите выяснить, виноват ли Боб в плагиате: определите, можно ли получить строку \(t\) из строки \(s\), вырезая из нее произвольное количество раз по два стоящих рядом символа.
Входные данные
В первой строке дана строка \(s\), состоящая из маленьких латинских букв от ‘a’ до ‘z’ (\(1 \le |s| \le 2 \cdot 10^5\)).
Во второй строке дана строка \(t\), также состоящая из маленьких латинских букв (\(1 \le |t| \le |s|\)).
Выходные данные
В качестве ответа выведите <<YES>>, если из \(s\) можно получить \(t\) удалениями двух символов подряд, и <<NO>> в противном случае.
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи и необходимых подзадач успешно пройдены.
| |
![]()
|
3/
3
|
|
Темы:
"Два указателя"
Дана строка s и символ с, который встречается в s. Для каждого символа из строки s, определите расстояние до ближайшего символа с.
Расстояние между двумя индексами i и j равно abs(i - j), где abs - функция вычисления модуля числа.
Формат входных данных
В первой строке записана непустая строка s, состоящая из маленьких английских букв (длина строки не превышает 104). Во второй строке записан символ c. Гарантируется, что в строке s содержится как минимум один символ c.
Формат выходных данных
Выведите в одной строке через пробел n чисел ai. Число ai - расстояние от символа с индексом i до ближайшего символа c (n равно длине строки s, 0 <= i < n). Числа выводить в порядке следоваения букв в исходной строке.
| |
![]()
|
128/
28
|
|
Темы:
"Два указателя"
Последовательность \([b_1, b_2, \ldots, b_k]\) называется битонической, если выполнены неравенства \(b_1 < b_2 < \ldots < b_i > \ldots > b_k\) для некоторого \(1 \le i \le k\).
Например, последовательности \([1]\), \([1, 2, 3, 2]\), \([1, 4, 10]\), \([3, 2]\) являются битоническими, а последовательности \([1, 1]\), \([2, 1, 3]\) — нет.
Задана последовательность \([a_1, a_2, \ldots, a_n]\). Требуется количество пар \((l, r)\) таких, что \(1 \le l \le r \le n\) и последовательность \([a_l, a_{l+1}, \ldots, a_r]\) является битонической.
Формат входных данных
Первая строка ввода содержит число \(n\) (\(1 \leq n \leq 300\,000\)).
Вторая строка ввода содержит \(n\) целых чисел: \(a_1, a_2, \ldots, a_n\) (\(1 \leq a_i \leq n\)).
Формат выходных данных
Выведите одно число — количество пар \((l, r)\), таких, что \(1 \le l \le r \le n\) и последовательность \([a_l, a_{l+1}, \ldots, a_r]\) является битонической.
В первом примере подходят следующие пары:
-
\((1, 1)\), последовательность \([1]\)
-
\((2, 2)\), последовательность \([1]\)
-
\((2, 3)\), последовательность \([1, 2]\)
-
\((2, 4)\), последовательность \([1, 2, 3]\)
-
\((2, 5)\), последовательность \([1, 2, 3, 1]\)
-
\((3, 3)\), последовательность \([2]\)
-
\((3, 4)\), последовательность \([2, 3]\)
-
\((3, 5)\), последовательность \([2, 3, 1]\)
-
\((4, 4)\), последовательность \([3]\)
-
\((4, 5)\), последовательность \([3, 1]\)
-
\((5, 5)\), последовательность \([1]\)
| |
![]()
|
64/
11
|
|
Темы:
Одномерные массивы
"Два указателя"
У Максимуса есть коллекция волшебных амулетов, каждый из которых обладает своей магической силой. Список имеющихся у него амулетов отсортирован в порядке неубывания магической силы. Вернувшись из очередного путешествия, Максимус составил список новых амулетов, предварительно отсортировав их по невозрастанию магической силы. Теперь у него два отдельных списка и он хочет объединить их в один упорядоченный по неубыанию список.
Он хочет сделать это как можно быстрее. Помогите ему отсортировать два этих списка. Максимус просит вас написать программу, которая будет работать за O(len(A)+len(B)).
Входные данные
Программа получает на вход два неубывающих списка, каждый в отдельной строке.
Выходные данные
Программа должна вывести последовательность неубывающих чисел, полученных объединением двух данных списков.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 5 7
2 4 4 5 |
1 2 4 4 5 5 7 |
| |
![]()
|
209/
42
|
|
Темы:
"Два указателя"
Лука часто ездит на сборы по программированию. Сборы длятся n дней. Лука фиксирует количество решенных задач в каждый день сборов. Лука считает сборы «эффективными», если только один непрерывный не нулевой промежуток дней (от l до r), когда выполнялись следующие условия по числу решенных задач:
1 <= l <= r <= n;al = al+1 = al+2 =…=ar;l = 1 или al-1 > al;r = n или ar < ar+1;
Примеры
Пусть массив A хранит информацию о решении задач за каждый день сборов, тогда:
1) массив A = [5, 3, 3, 2, 3, 3, 4] описывает «эффективные», по мнению Луки, сборы (промежуток в 1 день l = r = 4 удовлетворяет условию);
2) массив А = [2, 2, 2, 3, 4, 4, 5, 6, 7, 7, 8] также описывает «эффективные» сборы (промежут l = 1, r = 3 удовлетворяет условию);
3) массив А = [1, 2, 3, 4, 3, 2, 1] описывает не «эффективные» сборы (есть два промежутка удовлетворяющих условию l = r = 1 и l = r = 7).
Лука только что вернулся с очередных сборов по программированию и рассказал вам сколько задач ежедневно он решал. Определите, являются ли сборы, с которых вернулся Лука «эффективными» по его же мнению.
Входные данные
Первая строка содержит одно целое число n (1 <= n <= 2·105) — длину массива. Вторая строка n целых чисел ai (1 <= ai <= 109) — количество решенных Лукой задач в i-й день .
Выходные данные
Выведите YES, если сборы Луки оказались эффективными, и NO в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7
5 3 3 2 3 3 4 |
YES |
| 2 |
11
2 2 2 3 4 4 5 6 7 7 8 |
YES |
| 3 |
7
1 2 3 4 3 2 1 |
NO |
| |
![]()
|
18/
6
|
|
Темы:
Строки
Бинарный поиск по ответу
"Два указателя"
В этой задаче Вам требуется найти максимальную по длине подстроку данной строки, такую что каждый символ встречается в ней не более k раз.
Входные данные
В первой строке даны два целых числа n и k (1 ≤ n ≤ 100000, 1 ≤ k ≤ n ) , где n – количество символов в строке. Во второй строке n символов – данная строка, состоящая только из строчных латинских букв.
Выходные данные
В выходной файл выведите два числа – длину искомой подстроки и номер её первого символа. Если решений несколько, выведите любое.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 1
abb |
2 1 |
| 2 |
5 2
ababa |
4 1 |
| |
![]()
|
82/
23
|
|
Темы:
"Два указателя"
Пересечение множеств
С детства Максим был неплохим музыкантом и мастером на все руки. Недавно он самостоятельно сделал несложный перкуссионный музыкальный инструмент — треугольник. Ему нужно узнать, какова частота звука, издаваемого его инструментом.
У Максима есть профессиональный музыкальный тюнер, с помощью которого можно проигрывать ноту с заданной частотой. Максим действует следующим образом: он включает на тюнере ноты с разными частотами и для каждой ноты на слух определяет, ближе или дальше она к издаваемому треугольником звуку, чем предыдущая нота. Поскольку слух у Максима абсолютный, он определяет это всегда абсолютно верно.
Вам Максим показал запись, в которой приведена последовательность частот, выставляемых им на тюнере, и про каждую ноту, начиная со второй, записано — ближе или дальше она к звуку треугольника, чем предыдущая нота. Заранее известно, что частота звучания треугольника Максима составляет не менее 30 герц и не более 4000 герц.
Требуется написать программу, которая определяет, в каком интервале может находиться частота звучания треугольника.
Входные данные
Первая строка входного файла содержит целое число n — количество нот, которые воспроизводил Максим с помощью тюнера (2 ≤ n ≤ 1000). Последующие n строк содержат записи Максима, причём каждая строка содержит две компоненты: вещественное число fi — частоту, выставленную на тюнере, в герцах (30 ≤ fi ≤ 4000), и слово «closer» или слово «further» для каждой частоты, кроме первой.
Слово «closer» означает, что частота данной ноты ближе к частоте звучания треугольника, чем частота предыдущей ноты, что формально описывается соотношением: |fi−fтреуг.| < |fi−1−fтреуг.|
Слово «further» означает, что частота данной ноты дальше, чем предыдущая.
Если оказалось, что очередная нота так же близка к звуку треугольника, как и предыдущая нота, то Максим мог записать любое из двух указанных выше слов.
Гарантируется, что результаты, полученные Максимом, непротиворечивы.
Выходные данные
В выходной файл необходимо вывести через пробел два вещественных числа — наименьшее и наибольшее возможное значение частоты звучания треугольника, изготовленного Максимом. Числа должны быть выведены с точностью не хуже 10−6.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
440
220 closer
300 further |
30.0 260.0 |
| 2 |
4
554
880 further
440 closer
622 closer |
531.0 660.0 |
| |
![]()
|
2/
2
|
|
Темы:
"Два указателя"
Использование сортировки
Простые задачи на перебор
Жадный алгоритм
Задача на реализацию
У маленького Миши есть кубики, на каждом из которых написана одна английская строчная буква. Вчера он выкладывал кубики в два ряда. В первом ряду у Миши n кубиков с буквами, во втором - m кубиков с буквами. Так получилось, что в двух этих рядах нет совпадающих букв. Другими словами, ни одна буква не содержится одновременно в обоих рядах.
Сегодня маленький Миша решил продолжить играть с кубиками. Но теперь он берет один любой кубик из какого-либо ряда и составляет из них третий ряд, добавляя кубик всегда в конец. Маленький Миша никогда не берет более k кубиков подряд из одного и того же ряда. Миша закончил играть тогда, когда у него закончились кубики в каком-то одном ряду (в первом или во втором).
Наблюдавший за игрой папа заметил, что играя таким образом у Миши получилась лексикографически наименьшая строка. По известным двум строкам, которые образуются путем прочтения букв первого и второго ряда и числу k определите строку, которую получил маленький Миша.
Строка x лексикографически меньше строки y только и только тогда, когда выполняется одно из следующих условий:
- x является префиксом y, но x != y;
- в первой позиции, где x и y различаются, в строке x находится буква, которая стоит в алфавите раньше, чем соответствующая буква y.
Входные данные
Программа получает на вход несколько строк. В первой строке записаны три числа: n - количество кубиков в первом ряду, m - количество кубиков во втором ряду, k - целое число(1 <= n, m, k <= 100). Во второй строке записана строка a длиной n - строка, образованная прочтением букв, написанных на кубиках первого ряда. В третьей строке - строка b длиной m - строка, образованная прочтением букв, написанных на кубиках второго ряда.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 4 2
aaaaaa
bbbb |
aabaabaa |
| |
![]()
|
141/
28
|
|
Темы:
Бинарный поиск
"Два указателя"
Задача на реализацию
Томми очень любит читать. Он взял из библиотеки n книг (в i-й книге ai страниц, страницы нумеруются с 1). Томми очень бережно относится к книгам, поэтому каждую из них обернул в обложку. Но, так как у него не оказалось ни одной прозрачной обложки, он пронумеровал книжки от 1 до n и написал номер на обложке каждой книги.
Томми читает уже m дней подряд. Книги он читает строго по порядку, начиная с книги с номером 1. Каждый день он записывает на доску общее число страниц, которые прочитал к текущему дню.
Например, если бы Томми взял 2 книги и, при этом, в в первой книге 3 страницы, а во второй - 5 страниц, то прочитав в первый день 2 страницы, а во второй день - 4 страницы у Томми на доске было бы записано два числа 2 и 6.
Томми сделал небольшой перерыв, а когда вернулся к чтению понял, что забыл какую книгу читал и на какой странице остановился. Также он не хочет терять статистику, но желает исправить ее, дописав в какой день какую книгу он читал и на какой странице остановился. Помогите Томми, по записанным числам на доске, определить в какой день какую книгу он читал и на какой странице остановился.
Входные данные
Программа получает на вход несколько строк. Первая строка содержит два целых числа n и m (1 <= n, n <= 2·105) - количество книг, взятых Томми из библиотеки и количество дней, в течении которых Томми читал книги. Во второй строке следует последовательность a1, a2, ... an (1 <= a1<= 1010), где ai равно количеству страниц в i-й книге. В третьей строке следует последовательность d1, d2, ... dm (1 <= dj <= a1 + a2 +...+ an), где dj равно общему числу страниц, прочитанных Томми к j-му дню. Все dj заданы в порядке возрастания.
Выходные данные
Выведите m строк. В каждой строке выведите по два числа - номер книги k (1 <= k <= n) и номер страницы в этой книге s (1 <= s <= ak), на которой остановился Томми в текущий день.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 6
10 15 12
1 9 12 13 15 17 |
1 1
1 9
2 2
2 3
2 5
2 7 |
| 2 |
2 3
5 10000000000
5 6 9999999999 |
1 5
2 1
2 9999999994 |
| |
![]()
|
75/
26
|
|
Темы:
Одномерные массивы
"Два указателя"
Задача на реализацию
Алиса оставила для своего отца профессора Селезнева секретную последовательность a[1..n]. Чтобы ее не прятать, она решила написать ее на самом видном месте, но в другом порядке следования чисел. Профессор Селезнев знает, что Алиса переписала секретную последовательность в следующем виде:
- первым числом слева записано число
a1;
- первым числом справа записано число
a2;
- вторым числом слева (после
a1) записано число a3;
- вторым числом справа (то есть перед числом
a2) записано число a4;
- все остальные числа записаны аналогичным образом.
То есть, если бы секретная последовательность была a = [1, 2, 3, 4, 5, 6], то профессор бы увидел следующую последовательность [1, 3, 5, 6, 4, 2]. Профессор Селезнев очень торопился и успел только сохранить в компьютер последовательность, которую увидел. Напишите программу, которая покажет профессору исходную секретную последовательность.
Входные данные
Первая строка содержит размер последовательности n (1 <= n <= 300), записанной Алисой для своего отца. Вторая строка содержит n чисел ai (1 <= ai <= 109) - саму последовательность.
Выходные данные
Выведите исходную последовательность, которую Алиса выписывала для отца.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
1 3 5 6 4 2
|
1 2 3 4 5 6 |
| 2 |
1
23 |
23 |
| |
![]()
|
272/
111
|
|
Темы:
"Два указателя"
Конструктив
Жадный алгоритм
У Томми есть детская игрушка «cортировщик», с расположенными подряд n колышками. На каждом колышке сейчас не более одного диска (то есть на каком-то колышке диск есть, а на каком-то его нет). Томми хочет переложить имеющиеся диски на колышках таким образом, чтобы они образовывали неубывающую последовательность при просмотре слева направо. То есть на каждом следующем колышке количество дисков должно быть не меньше, чем на предыдущем. Какое минимальное количество дисков Томми необходимо переложить?
Обратите внимание, что какие- то колышки по окончанию сортировки могут быть пустыми. Какие-то колышки могут содержать более 1 диска.
Входные данные
Программа получает на вход в первой строке целое число n (1 <= n <= 105), количество колышек на «cортировщике». Следующая строка содержит n целых чисел a1, a2, ... an – наличие диска на соответствующем колышке (0 <= ai <= 1). число 0 означает, что на i-м колышке нет диска, 1 – диск есть.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8
0 0 1 1 1 1 1 1
|
0
|
| 2 |
11
1 1 0 0 1 0 0 1 1 1 0
|
3
|
| |
![]()
|
132/
64
|
|
Темы:
"Два указателя"
Префиксные суммы(минимумы, ...)
Дана последовательность из N чисел. Рассматриваются все её непрерывные подпоследовательности, в которых количество отрицательных чисел не превышает С. Найдите среди них подпоследовательность с максимальной суммой, длины L. В ответе укажите сумму найденной подпоследовательности.
Входные данные
В первой строке записаны 3 числа: количество чисел N (1 <= N <= 1 000 000), L и C (\(1 <= L, C <= N <= 1 000 000\)). Каждая из следующих N строк содержит одно число, не превышающее по модулю 1 000.
Пример организации исходных данных во входном файле (для L = 3 и С = 3):
5 3 3
1
-1
2
-2
3
В этом наборе можно выбрать несколько последовательностей, но с максимальной суммой равной 3 будет: 2+(-2)+3.
Ответ (для С = 3 и L = 3): 3.
| |
![]()
|
273/
75
|
|
Темы:
Массивы
"Два указателя"
Алгоритмы обработки
Громозека имеет последовательность целых чисел A длины N. Он сделает три среза в последовательности A и разделит ее на четыре (непустые) смежные подпоследовательности B, C, D и E. Положения срезов он выбирает произвольно. Пусть P, Q, R, S - суммы элементов в B, C, D, E соответственно. Громозека будет счастлив, когда абсолютная разница между максимумом и минимумом между P, Q, R, S будет минимальной. Найдите минимально возможную абсолютную разницу между максимумом и минимумом между P, Q, R, S.
Входные данные
В первой строке записано целое число N (1 <= N <= 2·105). Во второй строке записано N целых чисел Ai (1 <= Ai <= 109).
Выходные данные
Выведите на экран минимально возможную абсолютную разницу между максимумом и минимумом между P, Q, R, S.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
5
3 2 4 1 2 |
2 |
Если разделить A на B, C, D, E = (3), (2), (4), (1,2), то P = 3, Q = 2, R = 4, S = 1 + 2 = 3.
Здесь максимум и минимум среди P, Q, R, S равны 4 и 2, с абсолютной разницей 2.
Мы не можем сделать абсолютную разницу между максимумом и минимумом меньше 2, поэтому ответ - 2. |
| 2 |
10
10 71 84 33 6 47 23 25 52 64 |
36 |
|
| 3 |
7
1 2 3 1000000000 4 5 6 |
999999994 |
|
| |
![]()
|
20/
3
|
|
Темы:
"Два указателя"
Васю угостили конфетами, а он решил частью конфет поделиться со своим младшим братом Петей. Однако он хочет разделить конфеты не поровну, а по-братски.
Для этого Вася решил сыграть сам с собой в следующую игру. Он разложил конфеты на столе в несколько кучек, которые расположил в ряд. Если кучек не меньше двух, то из первой и последней в этом ряду кучек он выбирает ту, в которой меньше конфет. Пусть в наименьшей кучке оказалось B конфет. Тогда он B конфет перекладывает из первой кучки во вторую, и также B конфет перекладывает из последней кучки в предпоследнюю. При этом, естественно, одна из кучек (или даже две, если в первой и последней кучках конфет было поровну) становится пустой, и Вася забывает про ее существование. Он повторяет эти операции до тех пор, пока на столе не останется одна или две кучки.
Если останется одна кучка, то Вася все конфеты съест сам, а если две — то конфеты из первой кучки он съест сам, а из второй кучки отдаст Пете.
Напишите программу, которая по исходному распределению конфет в кучках определит, чем закончится Васина игра.
Входные данные
Начальное расположение кучек конфет будет описываться K парами чисел Ai, Ni, которые обозначают, что на столе выложено подряд Ni кучек конфет, по Ai конфет в каждой.
Во входном файле задано сначала число K (1≤K≤105). Затем идет K пар чисел Ai, Ni (1≤Ai≤100, 1≤Ni≤108). Общее количество кучек так же не превысит 108.
Выходные данные
В выходной файл выведите сначала 1 или 2 — количество кучек конфет, которые останутся в конце игры. Затем выведите соответственно одно или два числа — количества конфет в оставшихся кучках.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3
2 2
3 2
2 1 |
2
11 1 |
Исходно конфеты расположены в следующих кучках: 2 кучки по 2 конфеты, две кучки из 3-х конфет и одна из 2-х:
2 2 3 3 2
Далее по 2 конфеты перекладывается из 1 и 5кучек во 2 и 4, при этом и 1 и 5 кучки становятся пустыми, т.е. на столе остается только 3 кучки:
4 3 5
Теперь по 4 конфеты перекладываются из 1 и 3 кучек во 2-ю и на столе остается две кучки, игра заканчивается с результатом 11 1
|
| 2 |
1
1 7 |
1
7 |
Изначальноу нас 7 кучек по 1 конфете в каждой. После первого перекладывания получится следующая конфигурация:
2 1 1 1 1 2
После второго:
3 1 3
После третьего останется одна кучка с 7 конфетами. |
| 3 |
5
1 1
2 1
3 1
4 1
5 2 |
2
15 5 |
Изначально имеется 6 кучек:
1 2 3 4 5 5
После первого перекладывания получим:
3 3 4 6 4
После второго:
6 4 9 1
После третьего:
5 5 10
Наконец, получим:
15 5 |
| |
![]()
|
58/
2
|
|
Темы:
"Два указателя"
Кэрол Дэнверс, известная как Капитан Марвел противодействует флоту Скруллов. Каждый из
кораблей Скруллов имеет определенную мощность, выраженную натуральным числом.
Кэрол считает, что настолько сильна, что может не только вывести из строя флот, но и немного
развлечься. Внимательно изучив мощность корабля, она решила, что будет выводить их из строя
в следующем порядке: каждый раз Кэрол будет атаковать тот корабль из неатакованных ранее,
мощность которого является медианой мощностей оставшихся кораблей.
Медиану ряда чисел Кэрол вычисляет следующим образом:
• Если количество чисел в ряду нечетно, то медиана — число, стоящее посередине упорядоченного по возрастанию данного ряда.
• Если количество чисел в ряду чётно, то медианой ряда является:
– Меньшее из двух стоящих посередине чисел упорядоченного по возрастанию данного ряда, если два средних различны.
– Любое из двух стоящих посередине чисел упорядоченного по возрастанию данного ряда,
если два средних равны.
Помогите Капитану Марвел посчитать порядок, в котором нужно атаковать корабли.
Формат входных данных
В первой строке дано одно натуральное число n — число кораблей во флоте Скруллов (1 <= n <= 105).
Во второй строке содержатся n натуральных чисел ai — мощность i-го корабля (1 <= ai <=109).
Формат выходных данных
Выведите n чисел — мощности кораблей в том порядке, в котором Кэрол будет их атаковать.
| Ввод |
Вывод |
|
3
8 3 19
|
8 3 19 |
|
4
4 2 2 1
|
2 2 1 4 |
| |
![]()
|
565/
201
|
|