| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Циклы
Условный оператор
Натуральные числа, которые можно выразить в виде суммы двух или более последовательных натуральных чисел, называются вежливыми числами. С другой стороны, натуральные числа, которые нельзя выразить подобным образом, называются невежливыми.
Ваша задача не только определить является натуральное число вежливым, но и подсчитать количество способов, которыми число можно выразить в виде суммы последовательных натуральных чисел. Для невежливых чисел это значение будет равно одному, а для вежливых - двум и более.
Например, число 42 - вежливое, и его можно выразить как
а) 3+ 4 + 5 + 6 + 7 + 8 + 9;
б) 9 + 10 + 11 + 12;
в) 13 + 14 + 15;
г) 42.
Число 512 будет невежливым, так как для него существует единственное представление
а) 512
Входные данные
Одно натуральное число N (N <= 106)
Выходные данные
Одно натуральное число - количество представлений N в виде суммы последовательных натуральных чисел
| |
![]()
|
6/
2
|
|
Темы:
Циклы
Арифметические операции
Белочка живет в дубовом парке. Каждый день до обеда она собирает ровно К желудей и складывает их в дупле одного из дубов. Последнее время вечером каждого воскресенья в парк приходит мальчик Витя. Он обнаружил дупло, в котором белочка хранит жёлуди. Для своих игр он каждый раз забирает Т желудей из дупла.
Известно, что после последнего прихода Вити в парк, в дупле осталось Х желудей. Необходимо определить через сколько дней после этого прихода Вити, белочка сможет собрать не менее М желудей в дупле.
Формат ввода
На вход программе в одной строке подается четыре целых числа, записанные через пробел К, M, Т, Х (1≤ К, M, Т, Х ≤109).
Формат вывода
Вывести одно целое число – количество дней, через которое белочка сможет собрать необходимое число желудей.
Если белочка не сможет собрать нужное число желудей никогда, вывести число -1.
| |
![]()
|
11/
2
|
|
Темы:
Строки
Циклы
Условный оператор
Прибор передает результаты измерений блоками информации. Каждый блок представляет собой набор цифр в шестнадцатеричной системе счисления (0123456789ABCDEF). Последняя цифра пятеричной записи суммы цифр блока показывает код ошибки, где 0 означает корректную передачу данных. Предпоследняя цифра пятеричной записи суммы цифр блока показывает тип результата:
0: «Излучение»
1: «Вспышка»
2: «Нагрев»
3: «Охлаждение»
4: «Перегрузка»
Определите количество результатов «Перегрузка», которые были переданы без ошибок после приема n блоков данных.
Формат ввода
В первой строке программе подается на вход число натуральное число n, не превышающее 1000.
Далее в каждой из n строк идет блок данных – набор цифр в шестнадцатеричной системе счисления (0123456789ABCDEF), длина блока не превышает 100 знаков.
Формат вывода
Вывести одно число – количество результатов «Перегрузка», которые были переданы без ошибок после приема n блоков данных.
| |
![]()
|
1/
1
|
|
Темы:
Циклы
Красная Шапочка отправилась на болото для сбора клюквы, чтобы испечь пирожки для бабушки. Клюквенное болото представляет собой координатную прямую. Берег, на котором стоит девочка, имеет координату 0, а клюквенная поляна — координату N + 1. В точках с координатами 1, 2, . . . , N расположены кочки. Первоначально у девочки E единиц энергии. Красная Шапочка может прыгнуть из точки x в точку y (x < y), потратив на это (y − x) единиц энергии, то есть затраченная энергия равна расстоянию между кочками. После того, как девочка приземлится на кочке с координатой i, она получает ai единиц энергии (при этом значение ai может оказаться отрицательным, тогда энергия Красной Шапочки уменьшится при приземлении). Нельзя, чтобы энергия Красной Шапочки в какой-либо момент оказалась меньше нуля. Например, Красная Шапочка не может прыгнуть с кочки 1 на кочку 3, имея одну единицу энергии, вне зависимости от того, сколько энергии она получит на 3-й кочке, так как для осуществления такого прыжка необходимо две единицы энергии.
Так как Красной Шапочке ещё надо вернуться обратно, девочке интересно, какое максимальное количество энергии у неё может оказаться, когда она достигнет поляны (точки с координатой N +1).
Формат входных данных
Первая строка входных данных содержит целое число E — первоначальный запас энергии Красной Шапочки, 1 ≤ E ≤ 109 . Вторая строка входных данных содержит целое число N — количество кочек на болоте, 1 ≤ N ≤ 105 . Следующие N строк содержат по одному целому числу ai — энергия, которую получает Красная Шапочка на i-й кочке, −2000 ≤ ai ≤ 2000.
Формат выходных данных
Программа должна вывести одно число — максимальное количество единиц энергии, которое останется у Красной Шапочки после достижения клюквенной поляны. Если девочка не сможет достигнуть цели, выведите одно число «-1» (без кавычек).
Замечание
В первом примере три кочки и первоначально 2 единицы энергии у Красной Шапочки. Она прыгает на кочку 1, что требует 1 единицу энергии, и у неё остаётся 1 единица энергии. На кочке 1 девочка получает 1 единицу энергии, и у неё становится 2 единицы энергии. Затем она прыгает с кочки 1 на кочку 3, потратив 2 единицы энергии, и у неё становится 0 энергии. Приземлившись на кочку 3, Красная Шапочка получает 1 единицу энергии, этого достаточно, чтобы перепрыгнуть с кочки 3 на поляну в точке 4, после чего у Красной Шапочки останется 0 единиц энергии.
Во втором примере у Красной Шапочки первоначально только 1 единица энергии, поэтому она может прыгнуть только на кочку 1, но значение a1 = −1, то есть после приземления на кочку 1 у Красной Шапочки энергия станет отрицательной, и она не сможет продолжить свой путь.
| |
![]()
|
24/
4
|
|
Темы:
Циклы
Вывод формулы
 Мумми-мама решила испечь печенье к празднику. Она печет по Мумми-мама решила испечь печенье к празднику. Она печет по B печений за один раз, и печёт их в следующие моменты времени: A минут, 2A минут, 3A минут и каждое последующее число, кратное A минутам после начала выпечки. Определите, сколько печений будет испечено Мумми-мамой к празднику, который наступит через T+0,5 после начала выпечки.
Формат входных данных
Программа получает на вход одну строку, содержащую три числа A, B и T. 1 <= A, B, T <= 20, A <= T. Все числа целые положительные.
Формат выходных данных
Выведите одно число - ответ на задачу.
| |
![]()
|
1614/
550
|
|
Темы:
Циклы
Условный оператор
На прямой тропинке на расстоянии 1 метр друг от друга сидят два кузнечика. Время от времени один из кузнечиков прыгает на несколько сантиметров влево или вправо. Требуется узнать, каково было минимальное расстояние, на которое сближались кузнечики в процессе прыжков. (Расстояние считается только в те моменты, когда оба кузнечика сидят на земле).
Входные данные
В первой строке вводится одно число N (1 ≤ N ≤ 100) – общее количество прыжков, а затем N чисел, описывающих прыжки. Модуль числа равен длине прыжка в сантиметрах; число отрицательное, если кузнечик начинал этот прыжок по направлению к другому кузнечику, и положительное – если от другого кузнечика. Числа по модулю не превосходят 100 и все отличны от 0. (Кузнечики могут перепрыгивать друг через друга. Гарантируется, что кузнечики не приземляются друг на друга.)
Выходные данные
Требуется вывести одно число – минимальное расстояние в сантиметрах, на которое сближались
| |
![]()
|
4/
2
|
|
Темы:
Целые числа
Циклы
Громозека является одним из ведущих в Галактике космических археологов. Возвращаясь домой с очередной археологической экспедиции, он решил привезти своим четырем детям их любимые печенья. Ему осталось только вбить необходимое количество килограмм на экране терминала, и автомат сразу выдаст ему печенье . Но, вот незадача, на терминале сломались все кнопки с цифрами и буквами. Работают только цифры 0 и 1. Громозека в задумчивости, как же ему заказать ровно n килограмм. Он придумал, что может сделать несколько заказов таким образом, чтобы каждый заказ мог состоять только из цифр 0 и 1. Вот только Громозека очень торопится, потому что до старта корабля осталось совсем немного времени. Помогите Громозеке определить минимальное число раз, которым ему придется воспользоваться автоматом, чтобы купить ровно n килограмм и порадовать своих детей!
Например, чтобы купить 12 киллограмм печенья Громозека может воспользоваться автоматом дважды, купив сначала 11 килограмм печенья, затем - 1 килограмм.
Входные данные
Программа получает на вход целое число n (1 <= n <= 109).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1234
|
4
|
| |
![]()
|
28/
14
|
|
Темы:
Циклы
В параде принимают участие M военных. Командование парада решило, что наиболее эффектное построение военных – в форме квадрата, то есть число участников построения должно быть точным квадратом. Но поскольку число M может не быть точным квадратом, разрешается разбить военных на несколько полков, каждый из которых строится в форме квадрата. Для красоты все полки должны быть одинакового размера, также командование парада хочет, чтобы размер каждого полка был как можно больше. Определите максимально возможный размер полка.
Входные данные
Программа получает на вход одно целое положительное число M, не превосходящее 2×109, – количество участников парад.
Выходные данные
Программа должна вывести одно число – максимально возможный размер полка.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
180
|
36
|
| |
![]()
|
112/
53
|
|
Темы:
Циклы
Эпическое соревнование проводится по почти олимпийской системе. Среди n команд, в несколько туров определяют единственную команду-победительницу по следующим правилам.
- Если количество команд, участвующих в очередном туре, четное, то команды разбиваются по парам. Эти пары соревнуются между собой (т.е. проводится
n/2 матчей) и в следующий раунд выходит ровно половина команд (команды всегда соревнуются между собой до победы какой-либо команды);
- Если количество команд, участвующих в очередном туре нечетное, то перед началом этого тура проводится лотерея, которая определит ту одну удачливую команду, которая получит пропуск в следующий раунд. Оставшиеся команды опять разбиваются на пары и соревнуются между собой (т.е. сыграют между собой
n/2 матчей).
Вас же просят определить количество матчей, сыгранных в соревновании до определения победителя.
Входные данные
Программа получает на вход натуральное число n (1 <= n <= 200) - количество команд, которое участвует в соревновании.
Выходные данные
Выведите единственное число - ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 |
6 |
| |
![]()
|
17/
11
|
|
Темы:
Циклы
Айвен обладает волшебной палочкой, которая может делить кристаллы с волшебной силой N на несколько кристаллов. Айвен может одновременно поделить сразу два кристалла. В этом случае, они делятся на кристаллы, мощность которых строго больше 1 и, при этом, мощность каждого нового кристалла уникальна и кратна сразу мощностям исходных кристаллов.
Например, если исходные кристаллы имеют волшебную силу 12 и 6, то Айвен может разделить их на кристаллы мощностью 2, 3, 6
Для двух кристаллов с мощностями N и M выведите количество кристаллов, которые получатся после их деления.
Входные данные
Программа получает на вход два натуральных числа N и M - мощности исходных кристаллов (1<= N, M <= 1000). Каждое число вводится в отдельной строке.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12
6 |
3 |
| 2 |
25
30 |
1 |
| |
![]()
|
50/
20
|
|
Темы:
Циклы
Каждый юный волшбеник в течении первого учебного года прокачивает свою волшебную палочку. В конце года каждый волшебник отправляет своему главному магу свой идентификационный номер и мощность своей волшебной палочки. Далее, все списки от всех магов объединяются и получается единый список. Но, в процессе передачи была утерена информация об одном из идентификационных номеров. Вас просят помочь определить потерянный номер.
Всего в школе волшбеников N учащихся. Каждый учащийся имеет уникальный номер от 1 до N.
Входные данные
В первой строке входных данных записано целое число N (1 <= N <= 105 ) — количество юных волшебников. Следующие N-1 строк содержат по одному числу — идентификационные номера, которые попали в общий список в произвольном порядке. Среди этих чисел каждое число от 1 до N, кроме какого-то одного, встречается ровно один раз.
Выходные данные
Программа должна вывести одно число — потерянный идентификационный номер.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
2
5
1
3 |
4 |
| |
![]()
|
126/
27
|
|
Темы:
Циклы
В перерывах между отработкой заклинаний, Айвен любит лакомиться бобами. Бобы в волшебной школе имеют свою особенность. На каждом бобе написано некоторое целое число. Сегодня Айвен принес мешок, в котором лежит N бобов. Айвен хочет съесть только два боба, но такие чтобы произведение чисел, которые записаны на бобах было бы наименьшим среди всех пар бобов (пару образовывают любые два боба, лежащие в его мешке).
Определите это произведение.
Входные данные
В первой строке вводится число N (2 ≤ N ≤105) - количество бобов в мешке Айвена, а затем N целых чисел, по одному в строке - числа, записанные на бобах, в том порядке, в котором их доставал Айвен (каждое число мо модулю не превосходит 40000).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1
-3
2 |
-6 |
| |
![]()
|
167/
26
|
|
Темы:
Циклы
Айвен обладает волшебной палочкой, которая может делить кристаллы с волшебной силой N на несколько кристаллов. При этом, мощность исходного кристалла кратна мощности каждого нового кристалла, полученного в результате деления, а также, все мощности новых кристаллов уникальны и меньше мощности исходного кристалла . Например, если исходный кристалл имеет волшебную силу 12, то Айвен может разделить его на кристаллы мощностью 1, 2, 3, 4, 6
Для кристалла с волшебной силой N выведите в порядке возрастания мощность всех кристаллов, полученных в результате деления.
Если кристалл не возможно поделить по указанным правилам, то выведите -1.
Входные данные
Программа получает на вход натуральное число N - мощность исходного кристалла (N <= 100).
Выходные данные
Выведите в порядке возрастания мощность всех кристаллов, полученных после деления. Все значения необходимо вывести в одну строку, разделяя одним пробелом.
Если кристалл не возможно поделить по указанным правилам, то выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12 |
1 2 3 4 6 |
| |
![]()
|
173/
39
|
|
Темы:
Циклы
Цикл for
Простые задачи на перебор
Задача на реализацию
Громозека очень любит валерьянку. На его родной планете Чумароза можно купить за k чумриков (местная валюта) первую упаковку валерьянки, за 2·k чумриков - вторую и так далее (иными словами, за i-ю упаковку надо заплатить i·k чумриков). Громозека хочет купить w упаковок валерьянки. У него есть n чумриков. Сколько чумриков ему придется взять в кредит в чумарозском банке, чтобы купить w упаковок валерьянки?
Входные данные
В первой строке записано три положительных целых числа k, n, w (1 <= k, w <= 1000, 0 <= n <= 109), стоимость первой упаковки, изначальное количество чумарозиков у Громозеки и количество упаковок валерьянки, которые он хочет купить.
Выходные данные
Выведите единственное целое число - количество чумарозиков, которое Громозеке необходимо взять в кредит в банке. Если брать кредит не надо, выведите 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 17 4 |
13 |
| |
![]()
|
608/
160
|
|
Темы:
Циклы
Профессор Селезнёв анализирует сигналы из космоса. Он записывает в журнал интенсивность сигнала каждую секунду в виде целого числа. Делает это он до тех пор, пока сигнал не затухнет. Поэтому каждая запись его наблюдений заканчивается числом 0. Теперь он бы хотел узнать максимальную продолжительность по времени сигнала одной и той же интенсивности. Наблюдать сигналы Селезнёв может достаточно большой промежуток времени и посчитать максимальную продолжительность такого сигнала ему будет довольно сложно вручную. Помогите ему определить данный временной промежуток.
Входные данные
На вход программе подаются целые числа, по одному числу в строке. Последняя строка содержит число 0. (Число 0 - признак ее окончания).
Выходные данные
Максимальную продолжительность в секундах сигнала одной и той же интенсивности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
2
2
3
3
1
1
1
1
0 |
4 |
| |
![]()
|
246/
42
|
|
Темы:
Циклы
Арифметические алгоритмы (Теория чисел)
Сегодня мальчик Саша на уроке математики узнал про фракталы. Учитель показывал так называемую «кривую дракона». Она представляет собой геометрическую фигуру, которая строится следующим образом: на первом шаге проводится отрезок из начала координатной плоскости в точку (0; 1). Далее на каждом шаге из конца фрактала повторяется уже нарисованная часть фигуры, повернутая на 90 градусов против часовой стрелки (см. рисунок).
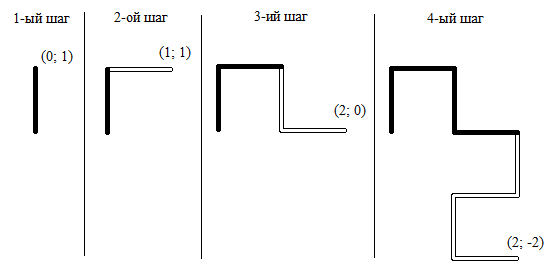
После уроков Саша попробовал сам изобразить «кривую дракона», и теперь он хочет знать, в какой точке координатной плоскости он закончил рисовать фрактал, проделав описанные выше N шагов. Требуется написать программу, которая по заданному числу N определяет координаты конца фрактала после выполнения N шагов.
Входные данные
Вводится одно целое число N (1 <= N <= 30).
Выходные данные
Выведите два числа через пробел - координаты конца фрактала.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 1 |
| 2 |
4 |
2 -2 |
| |
![]()
|
64/
24
|
|
Темы:
Целые числа
Циклы
Громозека и Алиса играют в следующую игру. Изначально, они ставят на числовую прямую три точки в целые координаты. Затем, один из них стирает любую крайнюю точку и ставит ее посередине между двумя оставшимися в координату с целым числом. Если между оставшимися точками четное количество целых чисел, то можно поставить точку в любую из них.
Например, если изначально стояли точки в координатах 3, 6, 8, то первым ходом можно стереть точку с координатой 3 и поставить ее в координату 7. Или стереть точку с координатой 8 и поставить ее в координату 4 или 5.
Чтобы долго не думать, Громозека и Алиса решили, что на каждый ход они будут тратить не более двух секунд.
Вас просят вычислить, какое максимальное количество секунд будет продолжаться игра, если известно начальное расположение трех точек.
Входные данные
Программа получает на вход три целых числа A, B и C (1<=A < B < C <= 1000). Каждое число записано с новый строки.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
6
8 |
4 |
| |
![]()
|
37/
15
|
|
Темы:
Вещественные числа
Циклы
Питание школьника, при грамотной организации, должно обеспечивать содержание белков, жиров и углеводов в соотношении 10%:30%:60% (допускается погрешность +/- 1%). Детский лагерь составляет меню, состоящее из N различных продуктов. Для каждого продукта известна энергетическая ценность в белках (P), жирах (F) и углеводах (C), а также количество каждого вида продукта в меню (K).
Определите, является ли составленное меню сбалансированным или нет.
Входные данные
Программа получает на вход несколько строк. В первой строке записано число натуральное число N (N <= 100) количество различных продуктов. В каждой из следующих N строк записаны по 4 числа: Pi, Fi, Ci и Ki. Все числа вещественные, не превосходят 103.
Выходные данные
Выведите YES, если меню сбалансированное, и NO в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 1 1 2
1 2 7 1
3 7 13 1 |
YES |
| |
![]()
|
313/
51
|
|
Темы:
Циклы
Цикл while
У исполнителя “Водолей” есть два сосуда, первый объемом A литров, второй объемом B литров, а также кран с водой. Водолей может выполнять следующие операции:
- Наполнить сосуд A (обозначается >A).
- Наполнить сосуд B (обозначается >B).
- Вылить воду из сосуда A (обозначается A>).
- Вылить воду из сосуда B (обозначается B>).
- Перелить воду из сосуда A в сосуд B (обозначается как A>B).
- Перелить воду из сосуда B в сосуд A (обозначается как B>A).
Команда переливания из одного сосуда в другой приводят к тому, что либо первый сосуд полностью опустошается, либо второй сосуд полность наполняется.
Входные данные
Программа получает на вход три натуральных числа A, B, N, не превосходящих 104.
Выходные данные
Необходимо вывести алгоритм действий Водолея, который позволяет получить в точности N литров в одном из сосудов, если же такого алгоритма не существует, то программа должна вывести текст Impossible.
Количество операций в алгоритме не должно превышать 105. Гарантируется, что если задача имеет решение, то есть решение, которое содержит не более, чем 105 операций.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
5
1
|
>A
A>B
>A
A>B
|
| 2 |
3
5
6
|
Impossible
|
| |
![]()
|
254/
29
|
|
Темы:
Циклы
На соревнованиях по шахматной композиции каждому участнику дается 10 задач для решения. За каждую задачу можно получить от 0 до 5 баллов. За правильно решенную задачу участнику начисляется 5 баллов. Если задача решена не полностью или не верно, то участнику дается вторая попытка. В этом случае за задачу участник получает балл равный среднему баллу за две попытки, округленный по правилам математики.
Баллы выставляются по порядку от первой до последней решенной задачи.
Маленький Витя Ч., участвуя на своем первом в жизни соревновании, забыл сколько задач он решил. Витя Ч. помнит, что получил всего 10 оценок, а также сами оценки по порядку.
Определите сколько всего задач решил Витя Ч., за сколько задач он получил максимальный балл с первой попытки, а также общую сумму баллов, которую он набрал.
Входные данные
Программа получает 10 строк, в каждой из которых записано по одному неотрицательному числу от 0 до 5.
Выходные данные
Выведите в первой строке количество задач, которые Витя Ч. успел решить, во второй строке - количество задач, которые решил с первой попытки на максимальный балл, в третьей строке - общее количество набранных баллов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
5
2
5
0
5
5
2
5
5 |
6
2
25 |
| |
![]()
|
95/
18
|
|