| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Целые числа
Перебор с отсечением
Бригада скорой помощи выехала по вызову в один из отделенных районов. К сожалению, когда диспетчер получил вызов, он успел записать только адрес дома и номер квартиры K1, а затем связь прервалась. Однако он вспомнил, что по этому же адресу дома некоторое время назад скорая помощь выезжала в квартиру K2, которая расположена в подъезда P2 на этаже N2. Известно, что в доме M этажей и количество квартир на каждой лестничной площадке одинаково. Напишите программу, которая вычилсяет номер подъезда P1 и номер этажа N1 квартиры K1.
Входные данные
Во входном файле записаны пять положительных целых чисел K1, M, K2, P2, N2. Все числа не превосходят 1000.
Выходные данные
Выведите два числа P1 и N1. Если входные данные не позволяют однозначно определить P1 или N1, вместо соответствующего числа напечатайте 0. Если входные данные противоречивы, напечатайте два числа –1 (минус один).
| |
![]()
|
1/
1
|
|
Темы:
Перебор с отсечением
В связи с проведением межпланетного шашечного турнира было принято решение о строительстве орбитальной гостиницы. Она должна была представлять собой большой куб из N×N×N блоков – маленьких кубиков 1×1×1, и каждый блок должен был быть окрашен снаружи со всех сторон в какой-то один цвет. При этом некоторые блоки могли быть покрашены в один и тот же цвет.
Через год были сделаны фотографии гостиницы с каждой из 6 сторон: спереди, слева, сзади, справа, сверху, снизу. За год эксплуатации могло случиться так, что из-за непрочного крепления некоторые блоки, из которых была построена гостиница, оторвались и улетели в открытый космос. Комиссия по восстановлению гостиницы хочет по сделанным снимкам установить максимальное возможное количество оставшихся блоков.
Итак, вам необходимо по видам гостиницы (куба N×N×N, из которого, возможно, выкинуты некоторые кубики 1×1×1) с 6 сторон определить, из какого максимального количества блоков 1×1×1 она может состоять. Может оказаться так, что гостиница состоит из двух или более не связанных между собой частей.
Входные данные
В первой строке входного файла находится число N — размер гостиницы (1≤N≤10). На следующих N строках записаны виды гостиницы с 6 сторон (в следующем порядке: спереди, слева, сзади, справа, сверху, снизу). Каждый такой вид представляет собой таблицу N×N, в которой различными заглавными латинскими буквами обозначены различные цвета, а символом «.» (точка) — то, что в этом месте можно будет смотреть прямо сквозь гостиницу. Два последовательных вида отделяются друг от друга ровно одним пробелом в каждой из N строк.
Нижняя граница вида сверху соответствует верхней границе вида спереди, а верхняя граница вида снизу — нижней границе вида спереди. Для видов спереди, сзади и с боков верх и низ вида соответствуют верху и низу гостиницы.
Входные данные корректны, то есть во входном файле описано состояние, которое может получиться.
Выходные данные
Выведите в выходной файл одно число — искомое максимальное количество оставшихся блоков в гостинице.
| |
![]()
|
1/
1
|
|
Темы:
Перебор с отсечением
Склад конторы MacroHard представляет собой прямоугольную комнату размером NxM. На складе нарисована разметка, состоящая из линий, параллельных стенам склада, которые разбивают его на NxM квадратов 1x1.
Фирма выпускает высокотехнологичное оборудование, используемое в самых различных областях жизнедеятельности. Исторически сложилось так, что все изделия, выпускаемые этой компанией, имеют форму равнобедренного прямоугольного треугольника. При этом ассортимент изделий столь велик, что бывают изделия практически любых размеров.
Размещать изделия на складе разрешается только так, чтобы хотя бы одна сторона изделия была параллельна какой-то из стен склада, и, вдобавок, все углы изделия находились в точках пересечения линий разметки склада. Рисунки 1,2,3 иллюстрируют неправильное положение изделий, а 4,5 –
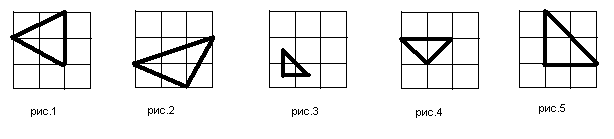
Руководство фирмы узнало, что склад планирует посетить Комиссия по неэффективному использованию складских помещений. Чтобы избежать выплаты крупного штрафа, фирма решила в срочном порядке поместить на склад изделия так, чтобы на складе не осталось свободного места. При этом было решено, что продукция, которая уже находится на складе, перемещаться не будет.
Напишите программу, которая определит, какое минимальное количество изделий можно добавить на склад, чтобы на нем не осталось свободного места.
Входные данные
В первой строке входного файла записаны три целых числа: N, M (размеры склада) и K (количество изделий, которые уже находятся на складе). Следующие K строк содержат по 6 целых чисел — координаты углов соответствующего изделия. Система координат введена так, что оси координат параллельны стенам склада и при этом один из углов склада имеет координаты (0,0), а противоположный — (N,M).
Ограничения
1<=N<=4, 1<=M<=4
Выходные данные
Первая строка выходного файла должна содержать одно число T — минимальное количество изделий, которые необходимо добавить, чтобы полностью заполнить склад. Каждая из следующих T строк должна содержать по 6 чисел — координаты углов изделий.
| |
![]()
|
1/
1
|
|
Темы:
Перебор с отсечением
Дата и время
Вывод формулы
Парламент некоторой страны принял новый закон о праздничных днях. Согласно этому закону первые K дней года, а также 23 февраля (День олимпиады по информатике) и 8 марта объявляются праздничными, а все остальные праздники отменяются. При этом все выходные (суббота и воскресенье), попавшие на праздничные дни, переносятся на следующие за этими праздниками рабочие дни.
В зависимости от того, на какой день недели приходится 1 января, количество нерабочих дней, которые идут подряд, может меняться.
Требуется определить, какое наибольшее количество нерабочих дней может идти подряд.
Входные данные
На вход подается единственное число K (1≤K≤50).
Выходные данные
Требуется вывести единственное число — наибольшее количество нерабочих дней, идущих подряд.
| |
![]()
|
6/
1
|
|
Темы:
Перебор с отсечением
Дан набор переменных x1, x2, ..., xN. Каждая переменная xi может принимать значение только -1, 0 или +1. Для данного целого числа S требуется определить количество способов присвоить переменным xi значения так, чтобы сумма всех возможных произведений xi * xj была равна S, где i < j и i, j = 1, 2, ..., N. Два способа считаются различными, если они содержат различное число xi = 0.
Ограничения: 2 <= N <= 10 000, -10 000 < S < 10 000.
Входные данные
В первой строке находятся числа N и S, разделённые пробелом.
Выходные данные
Вывести одно целое число - количество способов представить S как сумму произведений.
| |
![]()
|
1/
1
|
|
Темы:
Перебор с отсечением
Динамическое программирование: два параметра
Известный частный сыщик поставил чашку с чаем на специальную подогревающую подставку, питающуюся от USB-порта его компьютера, и приступил к обдумыванию очередного запутанного преступления. Через пару часов раздумий он понял, что для разгадки этого дела достаточно определить, была ли на месте преступления шахматная доска.
Недавно он получил по электронной почте фотографию места преступления. Подозрительный фрагмент (тот, на котором изображен предмет, похожий на шахматную доску) уже был скопирован в отдельный файл, но вдруг выяснилось, что, поскольку фотография была сжата с потерей качества, некоторые пиксели на ней из белых или черных стали серыми. Таким образом, определение того, является ли сфотографированный предмет шахматной доской, стало намного более сложным.
Все усложняется тем, что на фотографию могла попасть не вся шахматная доска, а лишь ее часть. Например, на приведенном рисунке на фотографию попала часть доски, у которой каждое поле имеет длину стороны, равную трем пикселям.
Помогите частному сыщику в расследовании преступления. Напишите программу, которая определит, может ли заданный фрагмент фотографии быть изображением части шахматной доски, и, если может, восстановит изображение шахматной доски до сжатия.
Шахматная доска — это квадрат, разбитый на \(x^2\) (для некоторого \(x\)) равных квадратов — полей. Стороны полей параллельны сторонам изображения. Длина стороны каждого поля шахматной доски выражается целым числом пикселей. Все пиксели, принадлежащие одному полю, покрашены в один и тот же цвет — черный или белый. При этом соседние поля (поля, имеющие общую сторону) покрашены в различные цвета.
Формат входных данных
Первая строка содержит два целых числа: \(m\) и \(n\) — размеры фрагмента фотографии в пикселях (\(1 \le m, n \le 250\)).
Следующие \(m\) строк содержат по \(n\) символов каждая, \(j\)-й символ \(i\)-й строки соответствует пикселю с координатами \((i, j)\). Символ <<.>> (точка) означает белый пиксель, символ <<*>> — черный, символ <<?>> — серый.
Формат выходных данных
Если заданный фрагмент фотографии может быть изображением части шахматной доски, выведите слово <<YES>>. После этого выведите \(m\) строк по \(n\) символов в каждой. Они должны содержать изображение соответствующей части шахматной доски в том же формате, что и во входных данных, только серые пиксели должны быть заменены на белые или черные. Если решений несколько, выведите любое.
В противном случае выведите слово <<NO>>.
| |
![]()
|
1/
1
|
|
Темы:
Перебор с отсечением
В одном магическом королевстве есть N городов, каждые два из которых соединены дорогой. Эти дороги были построены в давние времена Светлыми и Темными силами. Дороги, которые были построены Светлыми силами, вымощены белыми камнями, а те, что построены Темными – черными. Поскольку магические чары охраняют дороги, ни одно доброе существо не может пройти по дороге, вымощенной черными камнями, и ни одно злое – по белой дороге.
Когда-то давно люди решили избрать своих правителей и изгнали верховных магов из королевства. Однако недавно верховные маги Светлых и Темных сил договорились вернуть королевство под свой контроль. Для этого они хотят направить в некоторые города королевства магов, которые возьмут эти и смежные с ними города под свой контроль.
Точнее, если светлый маг будет направлен в некоторый город, то он возьмет под свой контроль этот город и все города, которые напрямую соединены с ним белыми дорогами. Аналогично, черный маг помимо города, в который он направлен, будет контролировать все города, напрямую соединенные с ним черными дорогами. Для захвата королевства требуется установить контроль над всеми городами.
Однако, при разработке плана захвата обнаружилось две трудности. Во-первых, выяснилось, что маг согласен принять участие в операции только если все маги, которые будут направлены в королевство, будут представлять ту же силу, что и он. То есть либо все участвующие в захвате маги должны быть светлыми, либо все они должны быть темными. Во-вторых, общее число магов, которые могут быть направлены в королевство не должно превышать K. Единственная надежда верховных магов заключается в том, что K достаточно велико, 2k >= N.
Выясните, светлых или темных магов следует использовать для захвата королевства, а также в какие города их следует направить.
Входные данные
В первой строке вводятся целые числа N и K ( 2≤N≤256, 2k ≥ N, K≤N).
Следующие N строк содержат по N целых чисел каждая. На i-ой позиции i-ой из этих строк расположено число 0, которое означает, что город не соединен дорогой сам с собой. Для всех j≠i число на j-ой позиции i-ой из этих строк равно 1, если i-ый город соединен с j-ым белой дорогой, и равно 2, если они соединены черной дорогой. Числа в строках разделены пробелами.
Гарантируется, что входные данные корректны, то есть если i-ый город соединен с j-ым белой дорогой, то и j-ый соединен с i-ым белой дорогой, аналогично в случае черных дорог.
Выходные данные
Если захватить королевство при заданных условиях невозможно, выведите единственное число 0. В противном случае в первой строке выведите 1, если удастся захватить королевство с использованием светлых магов, и 2, если требуется использовать черных магов. В следующей строке выведите число L≤K – количество использованных магов. Третья строка должна содержать L целых чисел – номера городов, в которые следует направить магов. Заметьте, что вам не требуется минимизировать L. Если решений несколько, выведите любое.
| |
![]()
|
28/
3
|
|
Темы:
Перебор с отсечением
Способы задания графа
Женя получил письмо от Леши со словесным описанием схемы метро в его городе. Метро содержит одну кольцевую линию. Каждая из остальных линий пересекается с кольцевой не более чем в двух местах, причем в точках пересечения организованы пересадочные станции. В одном месте кольцевую линию могут пересекать сразу несколько линий, имеющих общую пересадочную станцию.
Кроме этих пересадочных станций каждая из линий имеет не более одной пересадочной станции для перехода на другие, отличные от кольцевой, линии. На такой станции также может быть организована пересадка сразу на несколько линий.
Для каждой пересадочной станции Леша описал, какие линии на ней пересекаются, и указал порядок расположения пересадочных станций на кольцевой линии. Он утверждает, что все линии расположены на одной глубине и других пересечений, помимо пересадочных узлов, не имеют. Чтобы проверить это утверждение, Женя стал по словесному описанию рисовать схему метро, но у него не получилось.
Помогите Жене написать программу, которая будет проверять, действительно ли может существовать схема метро, соответствующая полученному описанию.
На рисунке приведена возможная схема метро, соответствующая второму примеру.
Формат входных данных
В первой строке содержится число \(k\) — количество линий метро в городе (\(1 \le k \le 10\)). Все линии пронумерованы от 0 до \(k - 1\), кольцевая линия имеет номер 0. Во второй строке записано число \(n\) — количество пересадочных станций. Каждая из следующих \(n\) строк описывает линии, пересекающиеся на соответствующей пересадочной станции, причем сначала следуют описания пересадочных станций, расположенных на кольцевой линии, в порядке их расположения на ней. Описание каждого узла начинается с количества пересекающихся в нем линий, затем следуют номера линий.
Формат выходных данных
Выведите слово YES, если по описанию можно построить схему метро, и NO в противном случае.
| |
![]()
|
1/
1
|