| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Динамическое программирование: два параметра
Элементарная геометрия
Поверхность Земли в горной местности можно представить в виде ломаной линии. Вершины ломаной расположены в точках (x1, y1), (x2, y2),…,(xN, yN), при этом xi<xi+1.
Обычный горный маг находится в точке (x1, y1) и хочет попасть в точку (xN, yN). При этом он может перемещаться только пешком. Он может ходить по поверхности Земли (т.е. вдоль ломаной). А может сотворить в воздухе мост и пройти по нему. Мост может соединять две вершины ломаной: мост не может начинаться и заканчиваться не в вершине ломаной, и мост не может проходить под землей (в том числе не может быть туннелем в горе), но мост может каким-то своим участком проходить по поверхности земли. Длина моста не может быть больше R. Суммарно маг может построить не более K мостов.
Какое наименьшее расстояние придется пройти магу, чтобы оказаться в точке (xN, yN).
Входные данные
Вводится сначала натуральное число N (2≤N≤100). Затем водится натуральное число K (1≤K≤100) — максимальное количество мостов. Далее вводится целое число R (0≤R≤10000) — максимальная возможная длина моста. Далее вводятся координаты (x1, y1), (x2, y2),…,(xN, yN). Все координаты – целые числа, не превышающие по модулю 10000, для всех i от 1 до N–1: xi<xi+1.
Выходные данные
Выведите одно число — минимальную длину пути, которую придется пройти магу (как по земле, так и по мостам). Ответ выведите не менее чем с 5 цифрами после десятичной точки.
| |
![]()
|
2/
2
|
|
Темы:
Динамическое программирование: два параметра
Динамическое программирование по подстрокам
Билл пытается компактно представить последовательности прописных символов от A до Z с помощью упаковки повторяющихся подпоследовательностей внутри них. Например, один из способов представить последовательность AAAAAAAAAABABABCCD - это 10(A)2(BA)B2(C)D. Он формально определяет сжатые последовательности символов и правила перевода их в несжатый вид следующим образом:
- Последовательность, содержащая один символ от A до Z, является упакованной. Распаковка этой последовательности даёт ту же последовательность из одного символа.
- Если S и Q - упакованные последовательности, то SQ - также упакованная последовательность. Если S распаковывается в S', а Q распаковывается в Q', то SQ распаковывается в S'Q'.
- Если S - упакованная последовательность, то X(S) - также упакованная последовательность, где X - десятичное представление целого числа, большего 1. Если S распаковывается в S', то X(S) распаковывается в S', повторённую X раз.
Следуя этим правилам, легко распаковать любую заданную упакованную последовательность. Однако Биллу более интересен обратный переход. Он хочет упаковать заданную последовательность так, чтобы результирующая сжатая последовательность содержала наименьшее возможное число символов.
Ограничения: длина исходной последовательности от 1 до 100.
Входные данные
В первой строке находится последовательность символов от A до Z.
Выходные данные
В единственной строке выводится упакованная последовательность наименьшей длины, которая распаковывается в заданную последовательность. Если таких последовательностей несколько, можно выводить любую.
| |
![]()
|
1/
1
|
|
Темы:
Динамическое программирование: два параметра
Динамическое программирование в играх
Однокопеечные монетки разложены в стопки (в стопках может быть различное количество монет), а стопки поставлены на столе в ряд слева направо. Двое противников по очереди делают ходы. Ход состоит в том, что один из игроков берет слева несколько стопок подряд, не меньше одной, но и не больше, чем перед этим взял его соперник. Первый игрок своим первым ходом берет не более K стопок. Игра заканчивается, когда стопок не остается. Требуется найти максимальное число монет, которое может получить первый участник после окончания игры, если второй игрок тоже старается ходить так, чтобы получить как можно больше монет.
Входные данные
В первой строке находится сначала число стопок N, за ним идут N чисел, задающих количество монет в стопках слева направо, а затем число K. Все числа в строке разделены пробелами.
Ограничения: 1 <= N <= 180, 1 <= K <= 80, количество монет в стопке - не менее 1 и не более 20 000.
Выходные данные
Вывести одно число - максимальное количество монет, которое заведомо может получить первый игрок, как бы ни играл второй.
| |
![]()
|
55/
13
|
ID 55128.
SMS
Темы:
"Длинная" арифметика
Динамическое программирование: два параметра
Сообщения SMS сотового телефона MOBILA составлены из прописных латинских букв. Если буква первая на кнопке, нужно нажать эту кнопку один раз, чтобы добавить букву в сообщение. Если буква вторая - нужно нажать кнопку дважды и т.д. Так, чтобы набрать слово "SMS", нужно нажать
(PQRS)(PQRS)(PQRS)(PQRS)(MNO)(PQRS)(PQRS)(PQRS)(PQRS)
Чтобы ввести две буквы, находящиеся на одной кнопке, нужно между нажатиями клавиши сделать паузу. Например, чтобы ввести сообщение "AA", нужно нажать
(ABC)(пауза)(ABC)
Если на кнопке три буквы, то, как только такая кнопка нажата три раза, последняя буква добавляется в сообщение немедленно, а следующие нажатия той же кнопки относятся к следующей букве сообщения. Аналогично, если на кнопке четыре буквы, то после четырёх нажатий в сообщение будет добавлена последняя буква. То есть последовательность нажатий
(ABC)(ABC)(ABC)(ABC)(пауза)(ABC)
соответствует сообщению "CAA". К сожалению, сотовые телефоны этой модели давно не производятся, и остался только один такой телефон. Он может произвольно вставлять и игнорировать паузы во время ввода сообщения, что может привести к некоторым изменениям в сообщениях. Например, введя MOSCOWQUARTERFINAL, можно получить вместо этого OMSCMNWQTTARTERPDEINAL. Вы получили SMS-сообщение и знаете, что оригинальное сообщение содержало N букв. Чтобы определить вероятность угадывания оригинального сообщения, найдите число возможных сообщений, которые могли превратиться в то, которое Вы получили.
Входные данные
В первой строке задана длина оригинального сообщения N. Вторая строка содержит полученное SMS-сообщение. 1 <= N <= 80, полученное сообщение состоит только из прописных латинских букв, длина полученного сообщения - от 1 до 80 букв.
Выходные данные
Вывести число сообщений из N букв, которые, будучи набранными на на этом телефоне, могут превратиться в данное сообщение.
| |
![]()
|
8/
1
|
|
Темы:
Динамическое программирование: два параметра
Дано N целых чисел A1, A2, ..., AN. Требуется найти количество различных значений сумм вида k1A1 + k2A2 + ... + kNAN.
(1 <= N <= 500, 0 <= Ai <= 100, 0 <= ki <= 1, все числа целые.)
Входные данные:
В первой строке находится число N, во второй - A1, A2, ..., AN через пробел.
Выходные данные:
Вывести одно число - количество различных значений сумм.
| |
![]()
|
3/
2
|
|
Темы:
Динамическое программирование: два параметра
N гангстеров собираются в ресторан. i-й гангстер приходит в момент времени T и имеет богатство Pi. Дверь ресторана имеет K + 1 степень открытости, они обозначаются целыми числами из интервала [0, K]. Степень открытости двери может изменяться на единицу в единицу времени, то есть дверь может открыться на единицу, закрыться на единицу или остаться в том же состоянии. В начальный момент времени дверь закрыта (степень открытости 0). i-й гангстер заходит в ресторан, только если дверь открыта специально для него, то есть когда степень открытости двери соответствует его полноте Si. Если в момент, когда гангстер подходит к ресторану, степень открытости двери не соответствует его полноте, он уходит и больше не возвращается. Ресторан работает в интервале времени [0, T]. Требуется собрать гангстеров с максимальным суммарным богатством в ресторане, открывая и закрывая дверь соответствующим образом.
Входные данные
В первой строке находятся числа N, K, T, во второй - T1, T2, ..., TN, в третьей - P1, P2, ..., PN. в четвёртой - S1, S2, ..., SN. Числа в строках разделены пробелами. 1 <= N <= 100, 1 <= K <= 100, 1 <= T <= 30 000, 0 <= Ti <= T, 1 <= Pi <= 300, 1 <= Si <= K, все числа целые.
Выходные данные
Вывести одно число - максимальное суммарное богатство гангстеров, попавших в ресторан. Если зайти не удалось никому, вывести 0.
| |
![]()
|
2/
2
|
|
Темы:
Динамическое программирование: два параметра
Перебор с отсечением
Известный частный сыщик поставил чашку с чаем на специальную подогревающую подставку, питающуюся от USB-порта его компьютера, и приступил к обдумыванию очередного запутанного преступления. Через пару часов раздумий он понял, что для разгадки этого дела достаточно определить, была ли на месте преступления шахматная доска.
Недавно он получил по электронной почте фотографию места преступления. Подозрительный фрагмент (тот, на котором изображен предмет, похожий на шахматную доску) уже был скопирован в отдельный файл, но вдруг выяснилось, что, поскольку фотография была сжата с потерей качества, некоторые пиксели на ней из белых или черных стали серыми. Таким образом, определение того, является ли сфотографированный предмет шахматной доской, стало намного более сложным.
Все усложняется тем, что на фотографию могла попасть не вся шахматная доска, а лишь ее часть. Например, на приведенном рисунке на фотографию попала часть доски, у которой каждое поле имеет длину стороны, равную трем пикселям.
Помогите частному сыщику в расследовании преступления. Напишите программу, которая определит, может ли заданный фрагмент фотографии быть изображением части шахматной доски, и, если может, восстановит изображение шахматной доски до сжатия.
Шахматная доска — это квадрат, разбитый на \(x^2\) (для некоторого \(x\)) равных квадратов — полей. Стороны полей параллельны сторонам изображения. Длина стороны каждого поля шахматной доски выражается целым числом пикселей. Все пиксели, принадлежащие одному полю, покрашены в один и тот же цвет — черный или белый. При этом соседние поля (поля, имеющие общую сторону) покрашены в различные цвета.
Формат входных данных
Первая строка содержит два целых числа: \(m\) и \(n\) — размеры фрагмента фотографии в пикселях (\(1 \le m, n \le 250\)).
Следующие \(m\) строк содержат по \(n\) символов каждая, \(j\)-й символ \(i\)-й строки соответствует пикселю с координатами \((i, j)\). Символ <<.>> (точка) означает белый пиксель, символ <<*>> — черный, символ <<?>> — серый.
Формат выходных данных
Если заданный фрагмент фотографии может быть изображением части шахматной доски, выведите слово <<YES>>. После этого выведите \(m\) строк по \(n\) символов в каждой. Они должны содержать изображение соответствующей части шахматной доски в том же формате, что и во входных данных, только серые пиксели должны быть заменены на белые или черные. Если решений несколько, выведите любое.
В противном случае выведите слово <<NO>>.
| |
![]()
|
1/
1
|
|
Темы:
Динамическое программирование: два параметра
Родители подарили мальчику Пете очень много одинаковых кубиков. Наиболее интересным сооружением из кубиков Петя счел двусторонние лесенки.
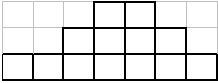
В основании (нижнем ряду) такой лесенки расположено N
кубиков, а каждый следующий ряд кубиков укладывается на предыдущий так, что один кубик укладывается ровно на один нижестоящий кубик, а по крайней мере на самый правый и самый левый кубики предыдущего ряда новые кубики не кладутся (чтобы получилась ступенька).
Петя поручил старшему брату подсчитать, сколько можно построить различных лесенок, состоящих из ровно K
рядов кубиков, в основании которых лежит ровно N
кубиков. При этом, если одну лесенку можно получить из другой путем зеркального отображения, то они все равно считаются различными.
Входные данные
Вводятся два числа N и K (1≤N≤100, 1≤K≤100).
Выходные данные
Выведите одно число – количество различных лесенок. Гарантируется, что правильный ответ не будет превышать 1018.
| |
![]()
|
3/
2
|
|
Темы:
Динамическое программирование: два параметра
Новый учитель математики ввел в школе оригинальную систему оценки учеников – рейтинговую. На каждом уроке школьнику предлагалось выполнить задание, состоящее из нескольких задач. После этого учитель увеличивал рейтинг школьника на число, равное отношению количества решенных им сегодня задач к количеству задач, решенных им на прошлом занятии. Например, если сегодня ученик решил 5 задач, а вчера – две, то к его рейтингу сегодня прибавится = 2.5. Изначально рейтинг равен нулю; он начинает увеличиваться со второго дня. Если в один из дней какой-то ученик не решал ни одной задачи, то учитель объявлял его полной бездарностью и переводил в другой класс (с облегченным изучением математики), поэтому каждый день все ученики старались решить хотя бы одну задачу.
Школьники быстро обнаружили, что для получения наибольшего рейтинга им далеко не всегда нужно решать все задачи. Им известно, сколько задач учитель будет давать в каждый из дней. Помогите им определить, в какой день сколько задач следует решить, чтобы в итоге получить наибольший рейтинг.
Входные данные
В первой строке вводится одно натуральное число N (1 ≤ N ≤ 1 000) – количество уроков, которые провел в школе учитель до того, как его уволили.
В следующей строке содержатся числа a1, a2, …, aN– количество задач, которые учитель предложил школьникам на первом, втором, …, N-м уроках соответственно (1 ≤ ai ≤ 100).
Выходные данные
В первой строке выведите максимальный рейтинг, который может получить школьник за N дней, с точностью не менее 0.001.
Во второй строке выведите N чисел – количество задач, которые должен решить школьник в каждый из дней. Если вариантов несколько, выведите один любой из них.
| |
![]()
|
12/
4
|
|
Темы:
Динамическое программирование: два параметра
Сколько целых последовательностей длины N, A = (A1,…,AN), удовлетворяют всем приведенным ниже условиям?
1) 1 <= Ai <= M (1 <= i <= N)
2)\(\sum\limits_{i=1}^NA_i \le K\)
Входные данные
На вход подается строка, содержащая три целых числа N, M (1 <= N, M <= 50), K (N <= K <= NM).
Выходные данные
Выведите на ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
2 3 4
|
6
|
(1,1) (1,2) (1,3) (2,1) (2,2) (3,1) |
| |
![]()
|
7/
3
|
|
Темы:
Динамическое программирование
Динамическое программирование: два параметра
Популярная сеть быстрого питания «McDuck's» открыла новый филиал в Берляндии. В ресторане установлено k плит. Для того чтобы приготовить бургер, надо жарить котлету в течение минуты на одной из плит, поэтому ресторан может готовить не более k бургеров в минуту.
Известно, что в «McDuck's» придут n клиентов. i-й из них придёт в момент времени ti, закажет xi бургеров и будет готов заплатить за них ci бурлей. Каждый клиент готов ждать заказ в течение w минут и, если через w минут после прихода он не получил xi бургеров, он не заплатит ничего. При этом каждый клиент готов получать только свежие бургеры, то есть только те, котлеты для которых были поджарены не раньше времени ti. Из-за таких сложных требований ресторан не всегда сможет выполнить все заказы всех клиентов.
Менеджеров ресторана заинтересовало, какую максимальную прибыль может получить «McDuck's». Помогите им ответить на этот непростой вопрос. Можно считать, что на готовку бургеров не расходуется никаких денег.
Входные данные
В первой строке содержатся три целых числа n, k и w (1 ≤ n ≤ 100000, 1 ≤ k ≤ 10, 1 ≤ w ≤ 60) — число клиентов, число плит и время ожидания клиента, соответственно.
Следующие n строк содержат описания клиентов, состоящие из трёх целых чисел — ti, xi, ci (1 ≤ ti, xi, ci ≤ 109) — время (в минутах) прихода i-го клиента, число бургеров, которые он закажет и число бурлей, которые он готов заплатить, соответственно. Клиенты перечислены в порядке возрастания времени прихода, то есть для любого i > 1 верно, что ti−1 ≤ ti.
Выходные данные
В единственной строке выведите одно число — максимальную прибыль ресторана.
Примечание
В первом тестовом примере первую котлету можно поставить жариться в момент времени 0 и тогда в момент времени 1 она будет готова и её можно будет дать в бургере первому клиенту. В момент времени 1 можно поставить жариться ещё одну котлету, она будет готова в момент времени 2 и её можно будет дать в бургере второму клиенту.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 1 1
1 1 5
1 1 7 |
12 |
| 2 |
3 2 2
1 6 8
2 5 10
3 4 4 |
12 |
| |
![]()
|
12/
2
|
|
Темы:
Динамическое программирование: два параметра
Миша установил на свой телефон новую игру «Мемтест 2к17». В ней предусмотрены ежедневные награды за посещение. Награды бывают n уровней. Тип награды зависит от награды за предыдущий день, а именно:
если игрок в предыдущий день не посещал игру, то за сегодняшнее посещение он получит награду уровня 1;
если игрок в предыдущий день зашёл в игру и получил награду уровня k ( k ≠ n ), то за сегодняшнее посещение он получит награду уровня k + 1 ;
если игрок в предыдущий день зашёл в игру и получил награду уровня n , то за сегодняшнее посещение он получит награду уровня 1.
На Форуме для Крутых Программистов Миша выяснил, что награды каждого из уровней составляют соответственно a 1 , a 2 , ..., a n золотых монет.
Через m дней состоится турнир по «Мемтест 2к17», к которому Миша хочет собрать как можно больше золотых монет. Помогите ему спланировать посещения игры на протяжении m дней, оставшихся до турнира. Найдите наибольшее количество золотых монет, которое он сможет получить за счёт ежедневных наград в этот период. Можно считать, что игра установлена в первый из этих m дней, то есть до этого Миша в неё ни разу не заходил.
Входные данные
Первая строка входных данных содержит натуральные числа n и m ( 1 ≤ n , m ≤ 1000 ) — количества уровней наград и дней до турнира.
Вторая строка входных данных содержит n целых чисел a 1 , a 2 , ..., a n ( 1 ≤ a i ≤ 1000 ), где a i — величина награды i -го уровня в золотых монетах.
Выходные данные
Выведите одно натуральное число — наибольшее количество золотых монет, которое Миша сможет получить до турнира.
Примечание
В первом тесте из примера Мише выгодно заходить в игру каждый день. Тогда он получит 1 + 2 + 4 = 7 золотых монет.
Во втором тесте из примера Мише выгодно заходить в игру в первый и третий день, получив в каждый из них по 4 монеты, тогда в сумме он получит 8 монет.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3
1 2 4 |
7 |
| 2 |
3 3
4 2 1 |
8 |
| |
![]()
|
52/
14
|
|
Темы:
Динамическое программирование: два параметра
Петя очень любит компьютерные игры. Недавно он обнаружил в интернете интересную ролевую игру. Управляя героем, надо искать магические артефакты и получать золото.
К сожалению, первый же квест в игре поставил Петю в тупик. Выполнив задание, он получил n магических артефактов, которые можно использовать для получения золота. Для каждого артефакта известна его ценность , для i -го артефакта она равна wi . Для получения золота артефакты можно активировать . Каждый артефакт можно активировать только один раз. Петя может активировать артефакты в произвольном порядке.
У героя, которым управляет Петя, есть магическая сила , исходно она равна нулю. Есть два способа активировать артефакт: с помощью магии и с помощью силы. Если активировать артефакт с ценностью w с помощью магии, то магическая сила героя увеличивается на w . Если же активировать артефакт с ценностью w с помощью силы, то герой получает xw золотых монет, где x — магическая сила героя в момент активации артефакта.
Например, если герой Пети получил 4 артефакта с ценностями 1, 1, 2 и 2, то можно получить 9 золотых монет, действуя следующим образом. Сначала надо активировать с помощью магии по одному артефакту с ценностью 1 и 2. После этого магическая сила героя равна 3, теперь можно активировать с помощью силы оставшиеся артефакты и получить 3 и 6 золотых монет, соответственно.
Помогите Пете определить, какое максимальное количество золотых монет он может получить, активировав артефакты в правильном порядке оптимальным образом.
Входные данные
Первая строка входных данных содержит единственное число n — количество магических артефактов ( 1 ≤ n ≤ 100 ).
Вторая строка входных данных содержит n чисел w1 , w2 , ..., wn — ценности артефактов ( 1 ≤ wi ≤ 100 ).
Выходные данные
Выведите максимальное возможное число золотых монет, которые можно получить с помощью магических артефактов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 1 2 2 |
9 |
| |
![]()
|
24/
10
|
|
Темы:
Динамическое программирование: два параметра
Дана прямоугольная доска N × M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить только так, как показано на рисунке:
Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.
Входные данные
Во входной строке находятся два натуральных числа N и M (\(1 <= N,\ M <= 15\)).
Выходные данные
Выведите единственное число количество способов добраться конём до правого нижнего угла доски.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 4 |
2 |
| 2 |
7 15 |
13309 |
| |
![]()
|
530/
214
|
|
Темы:
Динамическое программирование: два параметра
Дана прямоугольная доска N × M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить ТОЛЬКО на две клетки вниз и на одну клетку вправо, либо на две клетки вправо и на одну клетку вниз (смотри рисунок).
Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.
Входные данные
Во входной строке находятся два натуральных числа N и M (\(1 <= N,\ M <= 50\)).
Выходные данные
Выведите единственное число количество способов добраться конём до правого нижнего угла доски.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 4 |
2 |
| |
![]()
|
1048/
447
|
|
Темы:
Рекурсия
Динамическое программирование
Динамическое программирование: два параметра
Задача на реализацию
У Фермера Джона круглый амбар. Амбар состоит из кольца из n комнат, пронумерованных 1…n по периметру (3≤n≤1,000). Каждая комната имеет двери в две соседние комнаты и одну дверь во внешний мир.
ФД хочет разместить ровно ri коров в комнате i (1≤ri≤1,000,000). Он планирует открыть k внешних дверей (1≤k≤7), через которые коровы будут входить в амбар. Каждая корова затем идёт по часовой стрелке, пока не добредёт до нужной комнаты. ФД хочет открыть двери так, чтобы все коровы вместе прошли как можно меньшее расстояние. Коровы предварительно могут собраться как им выгоднее перед этими незакрытыми дверями (эти перемещения не входят в общее расстояние, учитываемое в задаче). Определите минимальное суммарное расстояние, которое придётся пройти коровам, если ФД наилучшим образом выберет какие k открыть.
ФОРМАТ ВВОДА:
Первая строка ввода содержит n и k. Последующие n строк содержат r1…rn.
ФОРМАТ ВВОДА:
Выведите минимальное суммарное расстояние пройденное коровами.
| Ввод |
Вывод |
|
6 2
2
5
4
2
6
2
|
14 |
ФД может открыть двери 2 и 5. 11 коров войдут в двери 2 и пройдут суммарное расстояние 8 чтобы попасть в комнаты 2,3,4. 10 коров войдут в дверь 5 и пройдут общее расстояние 6, чтобы попасть в комнаты 5,6,1.
| |
![]()
|
2/
1
|
|
Темы:
Динамическое программирование
Динамическое программирование: два параметра
Комбинаторика
Фермер Джон придумал игру для своих коров
Она играется на решётке R*C (2 <= R <= 750, 2 <= C <= 750), где каждый квадрат помечен целым числом от 1 до K (1 <= K <= R*C). Коровы выполняют последовательность прыжков, начиная в левом верхнем квадрате и заканчивая в правом нижнем квадрате и прыжок является корректным если и только если:
1) Вы прыгаете на квадрат c другим числом
2) Квадрат, куда Вы прыгаете, как минимум на одну строку ниже квадрата, в котором Вы сейчас стоите
3) Квадрат, в который Вы прыгаете как минимум на одну колонку правее квадрата, в котором Вы сейчас стоите
Пожалуйста, помогите коровам вычислить количество возможных различных последовательностей корректных прыжков из левого верхнего квадрата в правый нижний.
INPUT FORMAT:
Первая строка ввода содержит целые числа R, C, K. Каждая из следующих R строк содержит C целых чисел, каждое в интервале 1..K.
OUTPUT FORMAT:
Выведите количество различных способов пропрыгать из левого верхнего угла в правый нижний, по модулю 1000000007.
| Ввод |
Вывод |
|
4 4 4
1 1 1 1
1 3 2 1
1 2 4 1
1 1 1 1
|
5 |
| |
![]()
|
25/
5
|
|
Темы:
Строки
Динамическое программирование
Динамическое программирование: два параметра
Комбинаторика
Ферма Джона представлена решёткой N×N полей (1≤N≤500). Каждое поле представлено символом латинского алфавита. Например:
ABCD
BXZX
CDXB
WCBA
Каждый день корова Беси прогуливается из верхнего левого угла в правый нижний, каждый раз двигаясь на один шаг вправо или вниз. Беси записывает в строку буквы, по которым прошлась. Она огорчится, если у неё получится палиндром (слово, которое читается одинаково слева направо и справа налево), поскольку тогда она запутается, в каком направлении двигалась.
Пожалуйста, помогите Беси определить количество различных маршрутов которыми она может получить палиндромы. Различные пути, которыми получаются одинаковые палиндромы учитывать множество раз. Выведите свой ответ по модулю 1,000,000,007.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, и последующие N строк содержат N строк решётки, описывающей поля. Каждая строка содержит N символов в интервале A..Z.
ФОРМАТ ВЫВОДА:
Выведите количество различных путей Беси, формирующих палиндромы по модулю 1,000,000,007.
| Ввод |
Вывод |
|
4
ABCD
BXZX
CDXB
WCBA
|
12 |
Беси может сделать следующие палиндромы:
1 x "ABCDCBA"
1 x "ABCWCBA"
6 x "ABXZXBA"
4 x "ABXDXBA"
| |
![]()
|
4/
0
|
|
Темы:
Динамическое программирование
Динамическое программирование: два параметра
В зоомагазине нужно расставить в один ряд клетки с кошками и собаками. В ряд помещается N клеток, при этом есть одно ограничение: нельзя ставить подряд три клетки с животными одного вида (иначе они передерутся). Предполагается, что в магазине есть неограниченное количество клеток с кошками и собаками. Определите, сколькими безопасными способами можно расставить N клеток в ряд.
Входные данные
Входная строка содержит одно натуральное число – количество клеток в ряду N .
Выходные данные
Программа должна вывести количество безопасных способов расстановки N клеток в ряд.
| |
![]()
|
66/
47
|
|
Темы:
Динамическое программирование: два параметра
Динамическое программирование по подстрокам
Задан шаблон, состоящий из круглых скобок и знаков вопроса. Требуется определить, сколькими способами можно заменить знаки вопроса круглыми скобками так, чтобы получилось правильное скобочное выражение.
Входные данные
Вводится строка, которая содержит заданный шаблон длиной не более 80 символов.
Выходные данные
Выведите искомое количество способов. Исходные данные будут таковы, что это количество не превзойдет 2·109.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
????(? |
2 |
| |
![]()
|
305/
115
|
|