Динамическое программирование

ID 60878. Гигантский дракон

Канеки смотрит на неориентированный граф на плоскости из \(n\) вершин и \(m\) ребер. В этом графе ему интересно найти самого большого дракона.

Назовем сегментом дракона три ребра графа \(AL\), \(AB\) и \(AR\), имеющие общую вершину \(A\), и обладающие следующими свойствами:

• \(0 < \measuredangle (BAL) < 45^\circ\) и направление поворота от \(\overrightarrow{AB}\) к \(\overrightarrow{AL}\) — по часовой стрелке;

• \(0 < \measuredangle (BAR) < 45^\circ\) и направление поворота от \(\overrightarrow{AB}\) к \(\overrightarrow{AR}\) — против часовой стрелки;

• \(|AB| \geqslant |AL|\) и \(|AB| \geqslant |AR|\), то есть \(AB\) — максимальное по длине из трех ребер.

При выполнении всех указанных условий вершины \(A\) и \(B\) называются началом и концом сегмента, а ребра \(AL\), \(AB\) и \(AR\) — левой лапой, основанием и правой лапой сегмента, соответственно.

Определим дракона как последовательность сегментов, в которой

• начало первого сегмента \(A_1\), также называемое головой дракона, находится в вершине \(S\);

• \(A_{i} = B_{i-1}\) для всех \(i > 1\), то есть начало каждого следующего сегмента совпадает с концом предыдущего;

• \(\left|\measuredangle \left(\overrightarrow{A_{i-1} B_{i-1}}, \overrightarrow{A_i B_i}\right)\right| < 45^\circ\), то есть угол между векторами оснований соседних сегментов строго меньше \(45^\circ\);

• \(\left|\measuredangle \left(\overrightarrow{A_1 A_i}, \overrightarrow{A_i B_i}\right)\right| < 45^\circ\), то есть угол между вектором от головы дракона \(A_1\) до начала сегмента и основанием сегмента строго меньше \(45^\circ\).

Обратите внимание, что здесь углы взяты по модулю, то есть каждый следующий сегмент может быть повернут относительно предыдущего на менее чем \(45^\circ\) как по, так и против часовой стрелки.

Мощностью дракона будем считать сумму квадратов длин оснований его сегментов, то есть \(\sum |A_i B_i|^2\). В заданном графе помогите Канеки найти дракона максимальной мощности с головой в вершине \(S\).

Формат входных данных
В первой строке входных данных даны три числа \(n, m, S\) (\(2 \leqslant n \leqslant 2\cdot 10^5\); \(1 \leqslant m \leqslant 4\cdot 10^5\); \(1 \leqslant S \leqslant n\)) — количество вершин и ребер в заданном графе и номер вершины, являющейся головой дракона.

В следующих \(n\) строках дано описание вершин графа. Каждая строка содержит два целых числа \(x_i\) и \(y_i\) — координаты \(i\)-й вершины (\(0 \leqslant x_i, y_i \leqslant 10^9\)). Гарантируется, что все вершины графа различны, то есть не существует двух вершин, обе координаты которых совпадают.

Далее следует пустая строка.

В следующих \(m\) строках дано описание ребер графа. Каждая строка содержит два целых числа \(u_i\) и \(v_i\) — номера вершин, соединенных \(i\)-м ребром (\(1 \leqslant u_i, v_i \leqslant n\); \(u_i \neq v_i\)). Гарантируется, что граф не содержит кратных ребер.

Формат выходных данных
В первой строке выходных данных выведите два числа \(k\) и \(ans\) — количество сегментов в драконе, имеющем максимальную мощность, и само значение его мощности.

В следующих \(k\) строках выведите описание сегментов в том порядке, в котором они образуют дракона. В качестве описания сегмента \(i\) выведите номера вершин \(L_i\), \(B_i\) и \(R_i\).

Будем считать, что дракон может состоять только из вершины \(S\). В таком случае количество сегментов и его мощность следует считать нулями.

Замечание
Графы, данные в первом, втором и третьем тесте условий, выглядят следующим образом.

• В первом тесте в качестве максимального дракона можно взять весь граф целиком;

• Во втором тесте ни одна тройка ребер не может быть взята в сегмент, так как не выполняется одно из обязательных условий;

• В третьем тесте максимальный дракон состоит из двух сегментов с основаниями \(9 \to 5\) и \(5 \to 1\) с лапами \((9 \to 8, 9 \to 7)\) и \((5 \to 3, 5 \to 2\)).

ID 60138. Простоватые числа

Назовём число простоватым, если произведение цифр этого числа в десятичной системе счисления является простым числом. Например, простоватым является число 12, а число 29 не является.

Требуется посчитать количество простоватых чисел от \(l\) до \(r\).

Напомним, что целое число \(p > 1\) называется простым, если оно имеет ровно два делителя: \(1\) и \(p\).

Формат входных данных
Первая строка содержит одно целое число \(l\) (\(1 \le l \le 10^{100\,000}\)).

Вторая строка содержит одно целое число \(r\) (\(l \le r \le 10^{100\,000}\)).

Обратите внимание, что числа во вводе не помещаются в стандартные типы данных для целых чисел в большинстве языков программирования, в частности, в C++. Необходимо каким-либо специальным образом считывать входные данные, например, в виде строки.

Формат выходных данных
Выведите количество простоватых чисел от \(l\) до \(r\).

ID 59851. Интересные числа

Будем назвать натуральное число интересным, если в его десятичной записи первая цифра совпадает с последней.

Дано число \(n\). Найдите количество интересных чисел, не превышающих \(n\).

Формат входных данных
На ввод подается целое число \(n\) (\(1 \le n \le 10^{18}\)).

Обратите внимание, что для считывания этого числа вам может понадобиться 64-битный тип данных (<<long long>> в C++, <<long>> в Java, <<int64>> в Паскале).

Формат выходных данных
Выведите одно целое число — количество интересных натуральных чисел, не превышающих \(n\).

ID 55454. Не в билетах счастье, а в их количестве

Люди, покупающие какие-либо билеты, часто пытаются понять, на сколько счастливый билет им попался. При этом определения счастья бывают различные. В общественном транспорте Кирова для нумерации билетов используются числа от 1 до n. Витя считает билет счастливым, если его номер делится на сумму его цифр. Помогите Вите определить количество счастливых билетов.

Входные данные
На вход подается число n (1 ≤ n ≤ 10¹²).

Выходные данные
Выведите количество счастливых билетов в диапазоне от 1 до n.

ID 55169. Формирование поезда

Компания, занимающаяся железнодорожными перевозками, получила заказ сформировать поезд, состоящий из определённого числа вагонов. Проблема в том, что у компании есть вагоны, выпущенные в разное время, так что каждый из вагонов может иметь один из двух видов сцеплений на каждом конце. У компании также есть один локомотив.

Сцепления и для локомотива, и для вагонов обозначены буквой A или B. Повернуть вагон или локомотив противоположной стороной невозможно.

Дана информация о вагонах и локомотиве. Требуется найти число способов сформировать разные поезда заданной длины из имеющихся видов вагонов. Дополнительным требованием является то, что тип сцеплений на каждом конце состава должен соответствовать типу сцеплений локомотива.

Поезда считаются различными, если при их сравнении от одного конца к другому выявляется хотя бы одно отличие.

Пример 1. Пусть у компании есть вагоны AA, AA, AB, BA, BA и локомотив AB. В поезде должно быть 4 вагона. Из данных вагонов можно сформировать только два различных поезда: BAAAABBA и BAABBAAA. Локомотив можно присоединить к поезду как с левого (используя сцепление B), так и с правого конца (используя сцепление A).

Пример 2. Пусть у компании есть только по одному вагону каждого типа (AA, AB, BA, BB) и локомотив AA, а поезд должен состоять из трёх вагонов. Существует три способа сформировать поезд: AAABBA, ABBAAA и ABBBBA.

Входные данные
В первой строке через пробел N - число вагонов, находящихся в распоряжении компании, и K - требуемая длина поезда в вагонах. Вторая строка описывает тип сцеплений локомотива. Следующие N строк описывают типы сцеплений вагонов. Описания даны как AB, AA, BB или BA.

Ограничения: 1 <= K <= N <= 40.

Выходные данные
В первой строке выводится слово "YES", если можно сформировать хотя бы один поезд, или "NO" - в противном случае.

Если поезд сформировать возможно, во второй строке должно указываться число способов это сделать.

ID 54499. Игра "Даты"

Играют двое. Задаётся какая-то дата 2020 года. Каждый игрок на своём ходе называет более позднюю дату, увеличивая на 1 или 2 либо день в месяце, либо месяц, но не то и другое сразу. При этом сочетание дня и месяца должно оставаться датой. Игрок, назвавший 31 декабря, проигрывает. Оба играют наилучшим образом. Исходя из заданной даты вывести, кто выиграет.

Входные данные
В первой строке находятся числа, обозначающие день и месяц.

Выходные данные
Вывести 1, если выигрывает первый (начинающий) игрок, или 2 - в противном случае.

ID 52269. Загадка у костра

Однажды Юрик оказался в лесу у костра, где собрались \(n\) человек. Оказалось, что некоторые из них знакомы друг с другом. Для удобства пронумеруем людей целыми числами от \(1\) до \(n\). Обозначим как \(d_i\) количество людей, сидящих у костра, с которыми знаком \(i\)-й человек. Неожиданно оказалось, что два человека с номерами \(i\) и \(j\) (\(i \ne j\)) знакомы друг с другом тогда и только тогда, когда \(d_i = d_j\).

Вернувшись домой, Юрик задумался, какое минимальное количество пар людей могли быть знакомы, чтобы выполнялось это условие?

Формат входных данных
Единственная строка содержит одно целое число \(n\) (\(1 \le n \le 5\,000\)) — количество людей.

Формат выходных данных
Выведите одно целое число — минимальное количество пар знакомых людей.

Замечание
Рассмотрим первый пример из условия. Возможны следующие варианты:

1. Любые два человека знакомы друг с другом. В этом случае количество пар знакомых людей равно \(\frac{4 \cdot 3}{2} = 6\).

2. Некоторые три человека попарно знакомы друг с другом, четвертый человек не знаком ни с кем. В этом случае количество пар знакомых людей равно \(3\).

ID 50984. Ребрендинг

Костя и Женя — создатели группы <<Бумага>> — после выпуска легендарного альбома решили создать новое музыкальное объединение <<дневные грузчики>>, для этого им нужно найти двух новых людей.

Они пригласили на кастинг \(n\) человек. Кастинг продлится \(q\) дней. В \(i\)-й из дней Костя и Женя хотят найти двух человек на отрезке с \(l_i\) по \(r_i\), которые больше всего подходят их объединению. Так как <<дневные грузчики>> занимаются современным искусством,  музыкальные навыки им не важны, и они смотрят лишь на внешние признаки: им хочется, чтобы разница роста двух людей была как можно меньше.

Помогите им, и для каждого дня укажите минимальную разницу роста людей с кастинга на данном отрезке!

Формат входных данных
В первой строке вам дано два числа \(n, q\) (\(2 \leqslant n \leqslant 4 \cdot 10^5, 1 \leqslant q \leqslant 10^6\)) — количество людей, которые пришли на кастинг, а также количество дней кастинга.

Во второй строке вам даны \(n\) чисел \(a_1, a_2, a_3, \ldots, a_n\) (\(1 \leqslant a_i \leqslant n\)) — рост каждого из кандидатов.

Также гарантируется, что все \(a_i\) различны.

В следующих \(q\) строках даны по \(2\) числа \(l_i, r_i\) (\(1 \leqslant l_i < r_i \leqslant n\)) — отрезок людей для рассмотрения в \(i\)-й день кастинга.

Формат выходных данных
Выведите \(q\) строк. В \(i\)-й строке должна быть минимальная разница роста между двумя кандидатами на отрезке в \(i\)-й день кастинга.

Примечание
В первом примере минимальная разность на отрезке \([1, 2]\) составляет \(2\) (\(3 - 1 = 2\)), на отрезке \([2, 3]\) – \(1\), на отрезке \([1, 3]\) также \(1\).

В третьем примере минимальную разность на отрезке \([4, 6]\) составляют числа \(3, 5\) (\(5 - 3 = 2\)). На отрезке \([1, 2]\) минимальную разность имеют числа \(2, 6\) (\(6 - 2 = 0\)). На отрезке \([3, 6]\) минимальную разность имеют числа \(1, 3\) (\(3 - 1 = 2\)). На отрезке \([1, 3]\) минимальную разность образуют числа \(1, 2\) (\(2 - 1 = 1\)).

ID 50982. Велепин и маркетинг

Знаменитый писатель Велепин очень продуктивен. Совсем недавно он подписал контракт с известным изданием, и теперь за \(i\)-й год ему нужно написать \(k_i\) романов. Для него это вообще не проблема: он может сколько угодно писать о самураях, космосе, пустоте, насекомых и оборотнях.

У него есть \(n\) постоянных читателей, каждый из которых в \(i\)-й год прочитает один из \(k_i\) романов, выпущенных Велепиным. Читатели очень любят обсуждать новинки, поэтому \(j\)-й из них будет доволен в течение года, если такой же роман, как и он, прочитают как минимум \(a_j\) человек, включая его самого.

Издание, с которым подписал контракт Велепин, очень современно: у него есть возможность контролировать, какое произведение прочитает каждый из поклонников. Оно не хочет издавать романы просто так, поэтому хотя бы один экземпляр каждого романа должен попасть в руки читателя. Издание надеется выиграть награду <<Издание \(q\)-летия>>, поэтому отдел маркетинга хочет узнать, какое максимальное количество постоянных читателей можно сделать довольными в течение каждого года, оптимально распределяя романы между ними. Так как в отделе маркетинга нет никого, кто мог бы это сделать, он обратился к вам за помощью.

Формат входных данных
В первой строке дано одно целое число \(n\) \((2 \leqslant n \leqslant 300\,000)\) — количество постоянных читателей Велепина.

Во второй строке дано \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) \((1 \leqslant a_j \leqslant n)\) — количество людей, которые должны читать тот же роман, что и \(j\)-й, чтобы он был доволен.

В третьей строке дано одно целое число \(q\) (\(1 \leqslant q \leqslant 300\,000\)) — количество лет, которые нужно проанализировать.

В каждой из следующих \(q\) строк дано по одному целому числу \(k_i\) \((2 \leqslant k_i \leqslant n)\) — количество романов, которые Велепин должен написать в \(i\)-й год.

Формат выходных данных
Выведите \(q\) строк, в каждой из них ровно одно число — максимальное количество человек, которые могут быть довольны в \(i\)-й год, если Велепин выпустит \(k_i\) романов.

В первом примере в первый год оптимальным является разделение \(1, 1, 1, 2, 2\) (первый роман читают первые три человека, а два последних — второй). Во второй год оптимальным решением является \(1, 1, 2, 2, 3\) (первый роман читает первый и второй человек, второй роман читает третий и четвертый человек, третий роман читает пятый человек). В третий год оптимальным будет разбиение \(1, 2, 2, 4, 3\). Соответственно количество довольных людей по годам будет \(5, 5, 3\).

ID 50980. Московские гориллы

Зимой обитателям Московского зоопарка очень скучно, в частности, это касается горилл. Вы решили развлечь их и принесли в зоопарк перестановку \(p\) длины \(n\).

Напомним, что перестановкой длины \(n\) называется последовательность целых чисел от \(1\) до \(n\), в которой каждое такое число встречается ровно один раз. Например, последовательности \([3, 1, 2]\) и \([1, 4, 2, 3]\) являются перестановками, а последовательности \([3, 4]\) и \([1, 2, 2, 3]\) нет.

У горилл помимо вашей оказалась и своя перестановка \(q\) длины \(n\). Они предложили вам посчитать количество пар целых чисел \(l, r\) (\(1 \le l \le r \le n\)), таких что \(\operatorname{MEX}([p_l, p_{l+1}, \ldots, p_r])=\operatorname{MEX}([q_l, q_{l+1}, \ldots, q_r])\).

Вы не хотите отказать гориллам, поэтому попытаетесь решить эту задачу.

\(\operatorname{MEX}\) последовательности — это минимальное целое положительное число, отсутствующее в этой последовательности. Например, \(\operatorname{MEX}([1, 3]) = 2\), \(\operatorname{MEX}([5]) = 1\), \(\operatorname{MEX}([3, 1, 2, 6]) = 4\).

Формат входных данных
Первая строка содержит одно целое число \(n\) (\(1 \le n \le 2 \cdot 10^5\)) — длину перестановок.

Вторая строка содержит \(n\) целых чисел \(p_1, p_2, \ldots, p_n\) (\(1 \le p_i \le n\)) — элементы перестановки \(p\).

Третья строка содержит \(n\) целых чисел \(q_1, q_2, \ldots, q_n\) (\(1 \le q_i \le n\)) — элементы перестановки \(q\).

Формат выходных данных
Выведите одно целое число — ответ на задачу.

Обратите внимание, что ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать и с типом int.

ID 50976. Лабиринт

Маленький Влад решил создать собственную компьютерную игру. Игра будет проходить на карте, состоящей из комнат, соединённых коридорами. По каждому коридору можно будет передвигаться в обе стороны. Кроме того, Влад планирует создать карту, в которой коридоров будет ровно на один меньше, чем комнат, а также между любой парой комнат можно будет пройти, используя только коридоры. Для того, чтобы пройти игру, игроку необходимо выполнять квесты.

Все квесты в игре имеют одинаковую структуру. Пусть на карте расположены \(m\) комнат. Тогда каждый квест задаётся парой комнат \(u\) и \(v\) (\(1 \le u \le v \le m\)). Для прохождения этого квеста игроку нужно переместиться из комнаты \(u\) в комнату \(v\). Для усложнения игры в каждой комнате, через которую пройдёт игрок (включая начальную и конечную комнату) необходимо решить загадку. Влад называет сложностью квеста минимальное количество загадок, которые надо решить, чтобы его пройти. В частности, сложность квеста, у которого начальная и конечная комната совпадает, равна \(1\), а сложность квеста, в котором начальная и конечная комнаты соединены коридором равна \(2\). Также Влад называет квест трудным, если не существует квеста с большей сложностью, чем данный.

Интересностью игры Влад называет количество трудных уровней. Влад решил создать игру с интересностью ровно \(n\). Поскольку Владу сложно придумывать новые загадки, помогите ему составить карту с минимальным числом комнат, которое может быть в игре с интересностью \(n\).

Формат входных данных
В первой строке задано целое число \(n\) (\(1 \le n \le 500\)) — требуемое количество трудных уровней.

Формат выходных данных
В первой строке выведите целое число \(m\) — минимальное количество комнат на карте.

В следующих \(m - 1\) строках выведите через пробел пары целых чисел \(u\) и \(v\), обозначающие коридор, между комнатами \(u\) и \(v\).

Если подходящих карт с минимальным числом комнат несколько, выведите любую из них.

Примечание
В первом примере карта выглядит так:

На этой карте есть 10 квестов. Обозначим за (u, v) квест, который начинается в комнате с номером u и заканчивается в комнате с номером v. Сложность квестов (1, 1), (2, 2), (3, 3) и (4, 4) равна 1, сложность квестов (1, 2), (1, 3) и (1, 4) равна 2, а сложность квестов (2, 3), (2, 4) и (3, 4) равна 3. Таким образом, трудными квестами являются квесты (2, 3), (2, 4) и (3, 4). Трудных квестов 3, значит интересность игры на данной карте равна 3.

Во втором тестовом примере карта выглядит так:

На этой карте есть 4 трудных квеста (2, 5), (2, 6), (3, 5) и (3, 6). Их сложность равна 4.

В третьем тестовом примере карта выглядит так:

На этой карте есть 5 трудных квестов (2, 8), (3, 8), (4, 8), (5, 8), (6, 8) со сложностью 4.

ID 50975. Оптимизация акции

В сети магазинов <<Мир>> при оплате карточкой Weeza действует акция. При оплате покупки, состоящей не менее чем из \(10\) товаров, плата за самый дешевый товар не берется. Если товаров не меньше 20, то не оплачиваются уже два самых дешевых товара и т.д.

Например, при одновременной покупке \(17\) товаров, покупатель потратит сумму денег равную стоимости только \(16\) самых дорогих из них, а при покупке \(20\) и \(37\) товаров придется заплатить только за \(18\) и \(34\) самых дорогих товара, соответственно.

Миша хочет купить в магазине <<Мир>> \(n\) дисков с альбомами его любимой музыкальной группы. Подобрав подходящие диски, Миша выложил их на ленту в супермаркете в некотором порядке. Так как Миша не только меломан, но и математик, он понял, что ему, возможно, удастся сэкономить, если платить не за все \(n\) товаров одновременно, а разбить их на несколько покупок и оплатить каждую покупку отдельно. Миша решил привлекать к себе как можно меньше внимания и, в частности, не менять порядок товаров на ленте. Таким образом, Миша может только разбивать товары на ленте на группы подряд идущих и платить за каждую группу в отдельности.

Миша, конечно, математик, но вот с арифметикой у него всегда были проблемы. Помогите Мише и скажите, за какую минимальную стоимость он сможет купить \(n\) дисков, разбивая товары на ленте на группы подряд идущих товаров и оплачивая каждую группу отдельно. При этом разные группы могут быть разной длины.

Формат входных данных
В первой строке находится одно число \(n\) (\(1 \leq n \leq 100\,000\)) — количество дисков на ленте.

Следующая строка содержит \(n\) чисел \(a_i\) (\(1 \leq a_i \leq 10^9\)) — стоимости дисков в порядке расположения на ленте.

Формат выходных данных
Выведите наименьшую возможную стоимость покупки всех дисков с учетом акции при оптимальном разбиении дисков на группы.

В первом примере Мише в любом случае придется оплатить все диски, так как суммарное количество товаров меньше \(10\).

Во втором тестовом примере оптимально во время первой покупки оплатить первые два диска, а за остальные диски заплатить во время второй покупки. Тогда не придется заплатить за диск стоимостью \(9\).

ID 50866. Модообразная последовательность

Даны два целых числа \(x\) и \(y\). Назовем последовательность \(a\) длины \(n\) модообразной, если \(a_1=x\), и для всех \(1 < i \le n\) значение \(a_{i}\) равно либо \(a_{i-1} + y\), либо \(a_{i-1} \bmod y\). Здесь \(x \bmod y\) обозначает остаток от деления \(x\) на \(y\).

Определите, существует ли модообразная последовательность длины \(n\), сумма элементов которой равна \(S\), и если существует, то найдите любую такую последовательность.

Формат входных данных
Первая и единственная строка содержит четыре целых числа \(n\), \(x\), \(y\) и \(S\) (\(1 \le n \le 200\,000\), \(0 \le x \le 200\,000\), \(1 \le y \le 200\,000\), \(0 \le S \le 200\,000\)) — длина последовательности, параметры \(x\) и \(y\), и необходимая сумма элементов последовательности.

Формат выходных данных
Если искомая последовательность существует, выведите в первой строке <<Yes>> (без кавычек). Далее, во второй строке выведите \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) через пробел — элементы последовательности \(a\). Если подходящих последовательностей несколько, выведите любую из них.

Если же последовательность не существует, выведите в единственной строке <<No>>.

Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки <<yEs>>, <<yes>>, <<Yes>> и <<YES>> будут приняты как положительный ответ.

Замечание
В первом примере условиям удовлетворяет последовательность \([8, 11, 2, 5, 2]\). Таким образом, \(a_1 = 8 = x\), \(a_2 = 11 = a_1 + 3\), \(a_3 = 2 = a_2 \bmod 3\), \(a_4 = 5 = a_3 + 3\), \(a_5 = 2 = a_4 \bmod 3\).

Во втором примере первый элемент последовательности должен равняться \(5\), поэтому последовательность \([2, 2, 2]\) не подходит.

ID 50692. Сумма

Задано целое положительное число \(n\). Требуется найти число способов представить его в виде суммы нечетных слагаемых. При этом разбиения, отличающиеся только порядком слагаемых, считаются одинаковыми.

Например, число 6 можно представить следующими способами: \(1+1+1+1+1+1\), \(1+1+1+3\), \(3+3\), \(1+5\).

Формат входных данных
На вход подается число \(n\) (\(1 \le n \le 1000\)).

Формат выходных данных
Выведите число способов представить \(n\) в виде суммы нечетных слагаемых.

ID 50576. Сумма минимумов

У Саши есть блокнот, состоящий из \(n\) листочков, пронумерованных от 1 до \(n\). На \(i\)-м листочке написано целое число \(a_i\).

Аня собирается разорвать блокнот на \(k\) частей, для этого она выбирает \(k-1\) число \(1 \le r_1 < r_2 < \ldots < r_{k-1} < n\) и разрывает блокнот так, что листки с 1 по \(r_1\)-й оказываются в первой части, листки с \((r_1+1)\)-го по \(r_2\)-й оказываются во второй части, и т.д., последняя \(k\)-я часть содержит листки с \((r_{k-1}+1)\)-го по \(n\)-й.

После того, как Аня разорвет блокнот, Саша найдет минимальное число в каждой из получившихся частей и сложит их. Аня хочет разорвать блокнот таким образом, чтобы получившаяся сумма была как можно больше. Помогите ей выбрать способ разорвать блокнот, чтобы максимизировать сумму минимальных значений.

Формат входных данных
Первая строка ввода содержит два числа: \(n\) и \(k\) (\(2 \le k \le n \le 300\)). Вторая строка содержит \(n\) целых чисел: \(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 10^9\)).

Формат выходных данных
На первой строке выведите максимальное значение суммы, которое удастся достичь Ане. На второй строке выведите значения \(r_1, r_2, \ldots, r_{k-1}\), которые ей необходимо выбрать. Если вариантов разорвать блокнот, чтобы максимизировать искомую сумму несколько, выведите любой из них.

Примечание
В приведенном примере Аня разорвала блокнот на части \([1, 10, 2]\), \([8]\), \([9]\), \([3, 5, 4]\) и \([7, 6]\). Искомая сумма равна \(1 + 8 + 9 + 3 + 6 = 27\).

ID 50563. Трамвай

Вася идет из школы домой вдоль проспекта, по которому ходят трамваи. Мама считает, что ему после школы полезно дышать свежим воздухом, поэтому настаивает, чтобы не менее \(K\) метров он прошел пешком. Вася при этом хочет попасть домой как можно быстрее (обязательно выполнив требование мамы).

Вдоль проспекта расположено \(N\) трамвайных остановок, которые находятся в точках \(a_1, a_2, \ldots, a_N\) (все координаты задаются в метрах). Школа находится около 1-й остановки, а дом — около остановки номер \(N\). Мальчик идет пешком со скоростью \(v\) метров в минуту. Трамвай едет со скоростью \(w\) метров в минуту (временем стоянки трамвая на остановках пренебрежем). В нулевой момент времени и далее с интервалом \(T\) минут от первой остановки в сторону Васиного дома отправляются трамваи. Вася выходит из школы также в момент времени 0. Сесть в трамвай и выйти из него можно только на остановке. При этом, если Вася приходит на остановку раньше трамвая, на который хочет сесть, то ему придется подождать, пока тот не подъедет. Вася идет пешком и едет на трамвае только в направлении от школы к дому.

Напишите программу, которая определит, когда Вася сможет оказаться дома.

Формат входных данных

Сначала вводится число \(N\) — количество остановок (\(1 \leqslant N \leqslant 2000\)). Далее заданы координаты остановок \(a_1, a_2, \dots, a_N\) (\(0 \leqslant a_1 < a_2 < \ldots < a_N \leqslant 10^9\)). Далее вводится интервал движения трамваев \(T\) (\(1 \leqslant T \leqslant 2000\)). Затем расстояние, не меньше которого Вася должен пройти пешком \(K\) (\(0 \leqslant K \leqslant 2000\)). Затем заданы скорости Васи \(v\) и трамвая \(w\) (\(1 \leqslant v \leqslant w \leqslant 10\,000\)). Все вводимые числа целые. \(K\) не превышает длины пути от школы до дома.

Формат выходных данных
В первую строку выведите не менее чем с пятью знаками после десятичной точки одно число — минимальное время, когда Вася сможет оказаться дома, пройдя пешком не менее \(K\) метров. Далее нужно вывести информацию о пути Васи. Занумеруем промежутки между соседними остановками числами от 1 до \(N-1\) (то есть промежуток между первой и второй остановками имеет номер 1, между второй и третьей — 2 и так далее). Следующая строка должна содержать количество промежутков, пройденных Васей пешком. Далее выведите номера этих промежутков в возрастающем порядке.

ID 50276. Непростые разбиения

Рассмотрим разбиения целого положительного числа \(n\) в сумму целых положительных чисел. Будем называть разбиение непростым, если слагаемые в нем упорядочены по неубыванию, причем среди слагаемых нет простых чисел.

Например, для \(n=5\) существует два непростых разбиения: \(1+1+1+1+1\) и \(1+4\).

Задано число \(n\). Выведите все его непростые разбиения на слагаемые.

Формат входных данных
На вход подается число \(n\) (\(1 \le n \le 70\)).

Формат выходных данных
Выведите все непростые разбиения \(n\) на слагаемые. Слагаемые разделяйте знаком <<+>>. Не выводите пробелы. Разбиения можно вывести в любом порядке.

ID 48921. Пазл

Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.

Школьники Алиса и Ибрагим — лучшие друзья. У Ибрагима скоро день рождения, и по этому поводу Алиса решила подарить ему новый пазл. Пазл можно представить в виде матрицы из \(2\) строк и \(n\) столбцов, каждый элемент которой \(0\) или \(1\). За один ход можно поменять местами два элемента, стоящие в соседних клетках.

Более формально, будем считать, что строки матриц пронумерованы сверху вниз от \(1\) до \(2\), а столбцы — слева направо от \(1\) до \(n\). Обозначим клетку на пересечении строки \(x\) и столбца \(y\) за \((x, y)\). Будем считать две клетки \((x_1, y_1)\) и \((x_2, y_2)\) соседними, если \(|x_1 - x_2| + |y_1 - y_2| = 1\).

Алисе не нравится, какой рисунок образуют клетки пазла в данный момент. Она придумала свой рисунок, с которым и планирует подарить Ибрагиму новый пазл, но для этого нужно привести пазл в соответствующее состояние.

В конце учебного года у Алисы очень плотное расписание, и она не хочет тратить на эту задачу много времени. Помогите Алисе найти минимальное количество ходов, за которое она может получить свой рисунок, или скажите, что это невозможно.

Формат входных данных
В первой строке вводится одно целое число \(n\) (\(1 \leq n \leq 200\,000\)) — количество столбцов в пазле.

Следующие две строки описывают рисунок, образованный пазлом в данный момент. В каждой строке вводятся \(n\) целых чисел, каждое из которых равно \(0\) или \(1\).

Следующие две строки описывают желаемый рисунок Алисы в том же формате.

Формат выходных данных
Если Алиса не ошиблась и её рисунок можно получить, найдите и выведите минимальное необходимое количество ходов, иначе выведите \(-1\).

В первом примере из условия подойдет следующая последовательность обменов:

\((2, 1), (1, 1)\)

\((1, 2), (1, 3)\)

\((2, 2), (2, 3)\)

\((1, 4), (1, 5)\)

\((2, 5), (2, 4)\)

Можно показать, что меньшим числом обменов обойтись нельзя, поэтому ответ равен \(5\).

Во втором примере из условия никакая последовательность ходов не приводит пазл к нужному виду.

ID 47746. Фишки-палочки

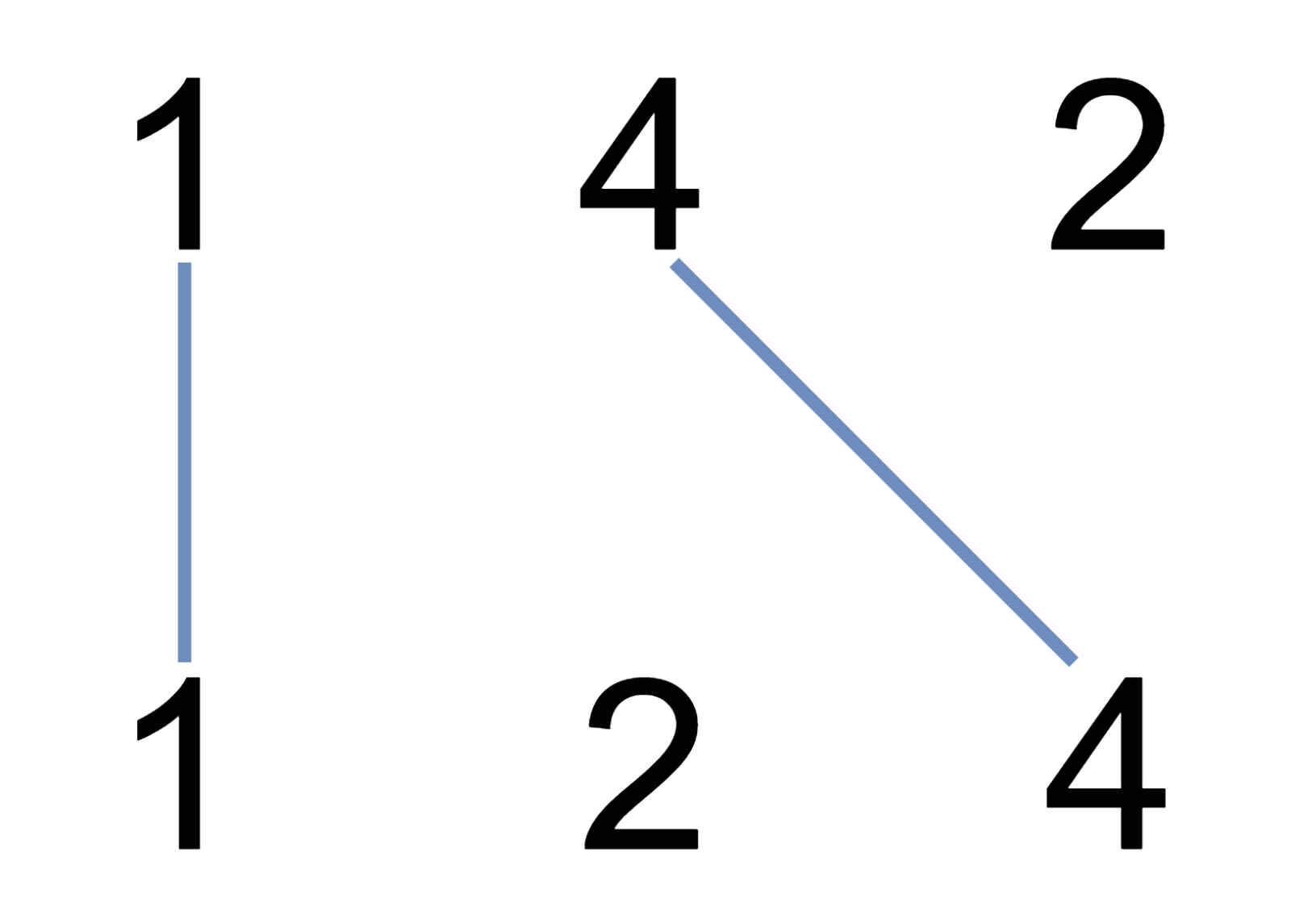
Алиса и Громозека играют в фишки-палочки. У каждого из них есть набор фишек, на каждой фишке записано одно целое число. Каждый из них  выкладывает свои фишки вдоль двух параллельных горизонтальных линий. Следующим шагом Алиса соединяет палочкой две фишки, расположенные на разных горизонтальных линиях, то есть соединяет одну свою фишку с одной из фишек Громозеки по следующим правилам:

1. числа, на фишке Алисы и на фишке Громозеки равны;
2. соединяющая палочка не должна пересекать другие палочки;
3. две палочки не могут указывать на одну и ту же фишку.

Далее, Громозека считает сколько палочек выложила Алиса. После этого, Алиса убирает свои палочки и фишки соединяет Громозека по тем же правилам. Выигрывает тот, кто выложит по данным правилам больше всего палочек. 

Вас, как наблюдателя за этой игрой, просят определить максимальное количество палочек, которые можно выложить по указанным правилам.


Входные данные
Первая строка входных данных содержит число n - количество фишек Алисы. Вторая строка содержит n чисел nums1i - числа на фишках Алисы, в том порядке, в котором она их выложила. Третья строка содержит число m - количество фишек Громозеки. Четвертая строка содержит m чисел nums2j - числа на фишках Громозека, в том порядке, в котором он их выложил. 

Ограничения

• 1 <= n, m <= 500
• 1 <= nums1[i], nums2[j] <= 2000

Выходные данные
Выведите одно число - максимальное количество палочек, которые можно выложить по указанным в условии задачи правилам игры.

Примечание
Рисунок к первому тестовому примеру

ID 47744. Айвен собирает кристаллы

Юный волшебник Айвен отправляется в волшебный лес, чтобы набрать  волшебных кристаллов. Каждый кристалл, растущий в данном лесу, обладает своей массой. Айвен имеет рюкзак, который может выдержать определенный вес M. Айвен хочет использовать свой рюкзак по максимуму и набрать  кристаллов такое количество, чтобы суммарно их вес равнялся в точности весу, который может выдержать его рюкзак. 
Вам стали известны массы кристаллов, которые растут в волшебном лесу. Выведите "YES",  если Айвен сможет набрать кристаллов суммарным весом ровно M, иначе выведите "NO".