| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Динамическое программирование
Деревья
Вычислительная геометрия
Канеки смотрит на неориентированный граф на плоскости из \(n\) вершин и \(m\) ребер. В этом графе ему интересно найти самого большого дракона.
Назовем сегментом дракона три ребра графа \(AL\), \(AB\) и \(AR\), имеющие общую вершину \(A\), и обладающие следующими свойствами:
-
\(0 < \measuredangle (BAL) < 45^\circ\) и направление поворота от \(\overrightarrow{AB}\) к \(\overrightarrow{AL}\) — по часовой стрелке;
-
\(0 < \measuredangle (BAR) < 45^\circ\) и направление поворота от \(\overrightarrow{AB}\) к \(\overrightarrow{AR}\) — против часовой стрелки;
-
\(|AB| \geqslant |AL|\) и \(|AB| \geqslant |AR|\), то есть \(AB\) — максимальное по длине из трех ребер.
При выполнении всех указанных условий вершины \(A\) и \(B\) называются началом и концом сегмента, а ребра \(AL\), \(AB\) и \(AR\) — левой лапой, основанием и правой лапой сегмента, соответственно.
Определим дракона как последовательность сегментов, в которой
-
начало первого сегмента \(A_1\), также называемое головой дракона, находится в вершине \(S\);
-
\(A_{i} = B_{i-1}\) для всех \(i > 1\), то есть начало каждого следующего сегмента совпадает с концом предыдущего;
-
\(\left|\measuredangle \left(\overrightarrow{A_{i-1} B_{i-1}}, \overrightarrow{A_i B_i}\right)\right| < 45^\circ\), то есть угол между векторами оснований соседних сегментов строго меньше \(45^\circ\);
-
\(\left|\measuredangle \left(\overrightarrow{A_1 A_i}, \overrightarrow{A_i B_i}\right)\right| < 45^\circ\), то есть угол между вектором от головы дракона \(A_1\) до начала сегмента и основанием сегмента строго меньше \(45^\circ\).
Обратите внимание, что здесь углы взяты по модулю, то есть каждый следующий сегмент может быть повернут относительно предыдущего на менее чем \(45^\circ\) как по, так и против часовой стрелки.
Мощностью дракона будем считать сумму квадратов длин оснований его сегментов, то есть \(\sum |A_i B_i|^2\). В заданном графе помогите Канеки найти дракона максимальной мощности с головой в вершине \(S\).
Формат входных данных
В первой строке входных данных даны три числа \(n, m, S\) (\(2 \leqslant n \leqslant 2\cdot 10^5\); \(1 \leqslant m \leqslant 4\cdot 10^5\); \(1 \leqslant S \leqslant n\)) — количество вершин и ребер в заданном графе и номер вершины, являющейся головой дракона.
В следующих \(n\) строках дано описание вершин графа. Каждая строка содержит два целых числа \(x_i\) и \(y_i\) — координаты \(i\)-й вершины (\(0 \leqslant x_i, y_i \leqslant 10^9\)). Гарантируется, что все вершины графа различны, то есть не существует двух вершин, обе координаты которых совпадают.
Далее следует пустая строка.
В следующих \(m\) строках дано описание ребер графа. Каждая строка содержит два целых числа \(u_i\) и \(v_i\) — номера вершин, соединенных \(i\)-м ребром (\(1 \leqslant u_i, v_i \leqslant n\); \(u_i \neq v_i\)). Гарантируется, что граф не содержит кратных ребер.
Формат выходных данных
В первой строке выходных данных выведите два числа \(k\) и \(ans\) — количество сегментов в драконе, имеющем максимальную мощность, и само значение его мощности.
В следующих \(k\) строках выведите описание сегментов в том порядке, в котором они образуют дракона. В качестве описания сегмента \(i\) выведите номера вершин \(L_i\), \(B_i\) и \(R_i\).
Будем считать, что дракон может состоять только из вершины \(S\). В таком случае количество сегментов и его мощность следует считать нулями.
Замечание
Графы, данные в первом, втором и третьем тесте условий, выглядят следующим образом.
-
В первом тесте в качестве максимального дракона можно взять весь граф целиком;
-
Во втором тесте ни одна тройка ребер не может быть взята в сегмент, так как не выполняется одно из обязательных условий;
-
В третьем тесте максимальный дракон состоит из двух сегментов с основаниями \(9 \to 5\) и \(5 \to 1\) с лапами \((9 \to 8, 9 \to 7)\) и \((5 \to 3, 5 \to 2\)).
| |
![]()
|
1/
1
|
|
Темы:
Вычислительная геометрия
В городе N есть \(m\) асфальтированных дорог, \(i\)-я дорога представляет собой отрезок между двумя точками \(A_{i}\) и \(B_{i}\) с координатами \((x^{A}_{i}, y^{A}_{i})\) и \((x^{B}_{i}, y^{B}_{i})\) соответственно.
В рамках тестирования новой технологии, которая позволяет переместить дорогу, мэр города N может демонтировать ровно одну любую дорогу и построить в любом месте ровно одну новую дорогу из полученного при демонтаже асфальта, при этом длина новой дороги должна не превосходить длину демонтированной дороги.
Проанализировав бюджет города, мэр понял, что в будущем он сможет обслуживать ровно три асфальтированные дороги.
Поэтому в рамках программы благоустройства мэр хочет выбрать три дороги, которые останутся асфальтированными, а также, возможно, переложить одну из них. Остальные асфальтовые дороги придется превратить в грунтовые. После этого три получившиеся дороги должны образовывать связный асфальтированный участок, то есть между любыми двумя асфальтированными точками должно быть можно добраться по асфальтированным дорогам.
Теперь мэр хочет понять, сколькими способами можно успешно завершить благоустройство города N: выбрать три дороги, чтобы выполнялись описанные условия.
Формат входных данных
В первой строке входных данных дано целое число \(m\) — количество асфальтированных дорог в городе (\(3 \leq m \leq 100\)).
Далее даны \(m\) строк. В \(i\)-й строке записаны четыре целых числа: \(x^{A}_{i}\), \(y^{A}_{i}\), \(x^{B}_{i}\), \(y^{B}_{i}\) — координаты точек \(A_{i}\) и \(B_{i}\) начала и конца \(i\)-й дороги соответственно.
Все координаты точек целые и по абсолютному значению не превосходят \(10^4\). Конечные точки любой дороги различны.
Формат выходных данных
В единственной строке выходных данных выведите одно целое число \(k\) — количество способов выбрать три дороги так, чтобы можно было успешно завершить благоустройство города N.
В примере из условия, чтобы успешно завершить благоустройство города N, можно выбрать три дороги одним из трех способов:
-
дороги \(\{1, 2, 3\}\) с координатами \((1, 1)-(2, 3)\), \((1, 3)-(2, 1)\), \((3, 1)-(4, 3)\) соответственно, и переложить дорогу \(3\), например, на новые координаты \((1, 4)-(2, 2)\)
-
дороги \(\{1, 2, 4\}\) с координатами \((1, 1)-(2, 3)\), \((1, 3)-(2, 1)\), \((2, 6)-(3, 6)\) соответственно, и переложить дорогу \(4\), например, на новые координаты \((1, 2)-(2, 2)\)
-
дороги \(\{2, 3, 4\}\) с координатами \((1, 3)-(2, 1)\), \((3, 1)-(4, 3)\), \((2, 6)-(3, 6)\) соответственно, и переложить дорогу \(4\), например, на новые координаты \((2, 1)-(3, 1)\)
Иллюстрация к способу a)
Перекладывание \(3\)-й дороги с координат \((3, 1)-(4, 3)\) на новые координаты \((1, 4)-(2, 2)\)
Иллюстрация к способу b)
Перекладывание \(4\)-й дороги с координат \((2, 6)-(3, 6)\) на новые координаты \((1, 2)-(2, 2)\)
Иллюстрация к способу c)
Перекладывание \(4\)-й дороги с координат \((2, 6)-(3, 6)\) на новые координаты \((2, 1)-(3, 1)\)
| |
![]()
|
3/
3
|
|
Темы:
Вычислительная геометрия
Рассматриваемые пирамиды имеют треугольник в основании, то есть являются тетраэдрами. Требуется по заданным длинам рёбер пирамиды найти её объём.
Ограничения: длины рёбер - целые положительные числа, не превосходящие 1000.
Входные данные
В первой строке находятся 6 чисел через пробел - длины рёбер пирамиды ABCD. Порядок рёбер: AB, AC, AD, BC, BD, CD.
Выходные данные
Вывести одно вещественное число с четырьмя знаками после запятой - объём пирамиды.
| |
![]()
|
1/
1
|
|
Темы:
Вычислительная геометрия
По координатам вершин многоугольника требуется найти координаты его центра тяжести. Стороны многоугольника друг с другом не соприкасаются (за исключением соседних - в вершинах) и не пересекаются. Площадь многоугольника не равна нулю.
Ограничения: число вершин 3 <= N <= 100 000, координаты вершин в декартовой системе координат целые и по модулю не превосходят 20 000.
Входные данные
В первой строке находится число N, в следующих N строках - пары чисел - координаты точек. Если соединить точки в данном порядке, а также соединить первую и последнюю точки, получится заданный многоугольник.
Выходные данные
Вывести два числа с двумя знаками после запятой - координаты центра тяжести.
| |
![]()
|
1/
1
|
|
Темы:
Вычислительная геометрия
На поверхности планеты, являющейся шаром радиусом R, заданы две точки своими широтой и долготой. Найти минимальную длину пути по поверхности этой планеты из одной точки в другую.
Входные данные
В первой строке находится число R, во второй строке заданы широта и долгота первой точки, в третьей строке - широта и долгота второй точки. Широта в градусах от -90 до 90, долгота в градусах от -180 до 180, 100 <= R <= 10 000, все числа вещественные.
Выходные данные
Вывести длину пути с двумя знаками после запятой.
| |
![]()
|
1/
1
|
|
Темы:
Вычислительная геометрия
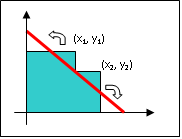
На плоскости дана геометрическая фигура "лестница". Она имеет N ступенек, которые заданы положительными координатами. Каждая ступень имеет свою высоту и ширину. Требуется найти прямую, которая отсекает от некоторых ступеней "лестницы" треугольники так, что из полученных фигур можно сложить прямоугольный треугольник такой же площади, что и исходная фигура. Разрешается, чтобы отсекаемые от ступеней треугольники соприкасались только вершинами (но не сторонами).
Формат входных данных:
В первой строке дано число 0 <= N <= 1000. Далее записаны N строк. Каждая строка содержит два целых чисел через пробел 0 < xi, yi < 106 - координаты вершины i-й ступени (ступени перечисляются в порядке сверху вниз, слева направо).
Формат выходных данных:
Ответ содержит одну строку: два числа через пробел - высота и ширина получившегося прямоугольного треугольника. Если существует несколько решений, то вывести любое. Результат выводится с точностью до четырех десятичных знаков после запятой. В случае, когда решение отсутствует, вывести два ноля через пробел
Примечание
| |
![]()
|
1/
1
|
|
Темы:
Вычислительная геометрия
Элементарная геометрия
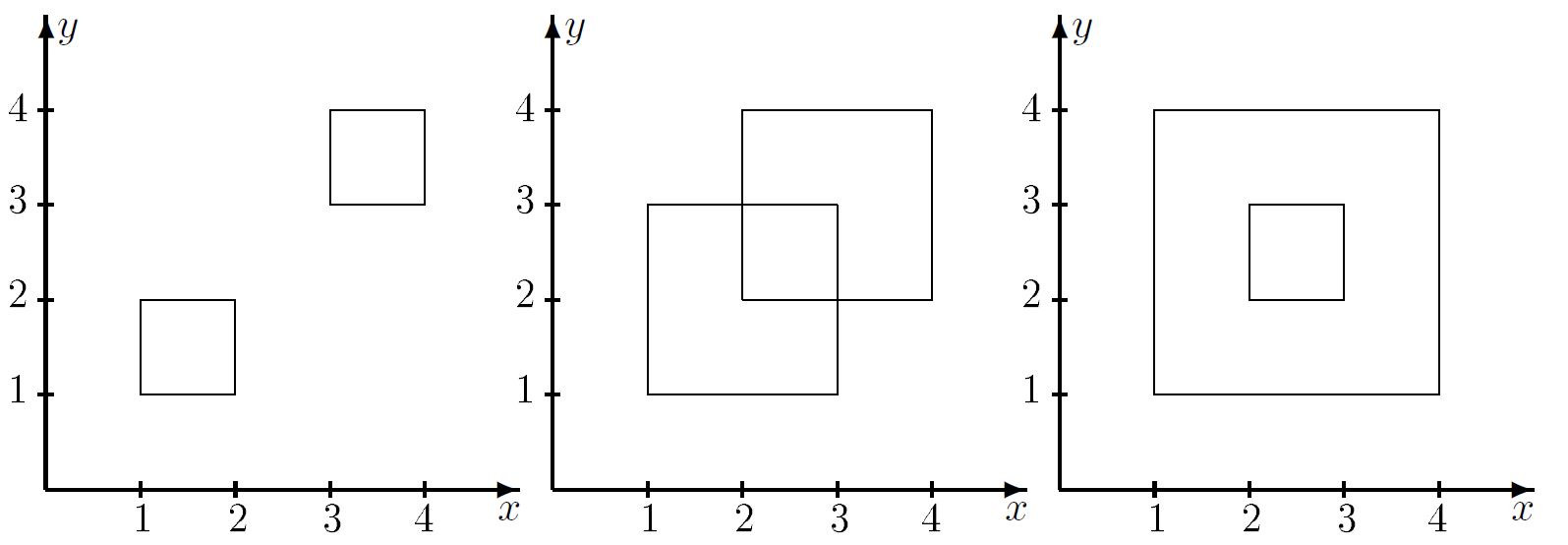
Петя нарисовал на клетчатом листке бумаги красивый рисунок прямоугольной формы. Его младшему брату Васе тоже захотелось порисовать, поэтому он вырезал из того же листка бумаги другой прямоугольник. При этом он не делал лишних разрезов, то есть в результате в листке осталась прямоугольная дырка. Кроме того, линии разреза не проходили (даже частично) по границам рисунка Пети. Более того, по границам рисунка не проходили даже продолжения линий разреза.
Ваша задача – по данным о расположении рисунка и прямоугольной дырки определить, испортил ли Вася рисунок старшего брата, другими словами, есть ли на вырезанном Васей прямоугольнике хотя бы маленький фрагмент рисунка Пети.
Формат входных данных
Вам даны 8 целых чисел - \(x_1, y_1, x_2, y_2, x_3, y_3, x_4, y_4\), где \((x_1, y_1)\) - координаты левого нижнего угла рисунка Пети, \((x_2, y_2)\) - координаты правого верхнего угла рисунка. Аналогично, \((x_3, y_3)\) - координаты левого нижнего угла вырезанного Васей прямоугольника, \((x_4, y_4)\) - координаты правого верхнего угла вырезанного прямоугольника. Гарантируется, что данные прямоугольники невырождены (\(x_1 < x_2\), \(y_1 < y_2\) и аналогичные неравенства для второго набора координат). Листок был не очень большим, поэтому каждое число по модулю не превосходит \(10^4\).
Формат выходных данных
Выведите YES, если Вася испортил рисунок, и NO в противном случае.
Примечание
| |
![]()
|
18/
4
|
|
Темы:
Вычислительная геометрия
Однажды злой волшебник Сарумян поглядел в видеочат и узрел там систему из N зеркал. Долго думал он, прежде чем внутренний голос подсказал ему, что система не простая. Он понял, что если посмотреть на эту систему под некоторым углом, и увидеть заданную точку А через все N зеркал (то есть так, чтобы его взгляд отразился через каждое из них ровно по одному разу, а потом попал в точку A), то откроются ему все тайны интернета.
Однако светлые силы не дремали и через агентурную сеть выяснили все про этот видеочат.
Требуется написать программу, которая подсказала бы светлым силам, под каким углом нужно посмотреть на систему зеркал, чтобы узнать все тайны интернета.
Входные данные:
В первой строке входного файла записано одно число – количество зеркал (0<N≤10). В следующей строке записаны координаты (x и y, где ось x направлена вправо, ось y – вверх) исходной точки (откуда надо смотреть на зеркала) и точки A. Далее в N строках записана информация о зеркалах – по четыре числа, обозначающие координаты начала и конца зеркала. Отражающая поверхность расположена на левой стороне зеркала (если смотреть от первой точки в направлении второй). С обратной стороны зеркала прозрачны.
Причем выполняются следующие ограничения:
• Все координаты вещественны и по модулю не превосходят 10000
• Никакие зеркала не пересекаются
• Конечная и начальная точки не лежат ни на одном из зеркал
Выходные данные:
В первую строку выходного файла необходимо записать YES, если решение существует, и NO, если нет. Если решение есть, то во вторую строку надо записать угол в градусах (с точностью до шести знаков после запятой), под которым нужно смотреть на зеркала. Угол отсчитывается против часовой стрелки от оси Ox и лежит в пределах от 0 до 360 градусов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
0 0
0 5
1 0 1 2
-1 4 –1 2 |
YES
51.340192 |
| |
![]()
|
5/
2
|
|
Темы:
Вычислительная геометрия
Задача на реализацию
Мальчик Вася очень любит геометрию. Кроме того, ему очень нравится забивать гвозди в доску. Сегодня он изучает свою любимую металлическую пластину, которую он собирается прибить к деревянной доске.
Пластина имеет форму, ограниченную многоугольником без самопересечений и самокасаний. В первой вершине многоугольника пластина имеет маленькую петлю.
Сначала Вася кладет пластину на доску, лежащую на горизонтальном столе, и прибивает ее гвоздем к пластине через петлю в первой вершине. Вбитый гвоздь жестко закрепляет положение первой вершины, однако позволяет пластине вращаться вокруг нее.
Теперь Вася хочет забить в доску еще один гвоздь, который бы ограничил вращение пластины, но он еще не решил куда. Он наметил m возможных позиций, куда он хотел бы забить гвоздь, и для каждой из них хочет узнать, на какой угол он сможет поворачивать свою пластину, если забьет в доску гвоздь в этой точке. При этом как только пластина касается гвоздя, дальше ее поворачивать нельзя.
Формат входных данных
В первой строке входного файла задано число n (3 ≤ n ≤ 2 000) — количество вершин многоугольника. В следующих n строках заданы координаты вершин многоугольника в порядке обхода. В следующей строке задано число m (1 ≤ m ≤ 2 000) — количество точек, которые Вася рассматривает как возможные положения второго гвоздя. В следующих m строках заданы координаты этих точек. Все эти точки находятся снаружи от исходного положения пластины. Все координаты во входном файле целые и не превосходят 106 по модулю.
Формат выходных данных
Выходной файл должен содержать m строк. В i-й строке выведите два вещественных числа αi и βi , где αi — максимальный угол в градусах, на который можно повернуть пластину по часовой стрелке, если Вася забьет гвоздь в i-ю точку, а βi — максимальный угол в градусах ,на который в этом случае можно повернуть пластину против часовой стрелки. Если гвоздь не мешает пластине поворачиваться, выведите αi = βi = 360. Ответ считается верным, если его абсолютная или относительная погрешность относительно правильного не превосходит 10−6 .
| Ввод |
Вывод |
4
0 0
-3 -3
0 -6
3 -3
3
-8 0
-2 0
2 -1 |
360.000000000000 360.000000000000
45.000000000000 225.000000000000
251.565051177078 18.434948822922 |
Пояснение
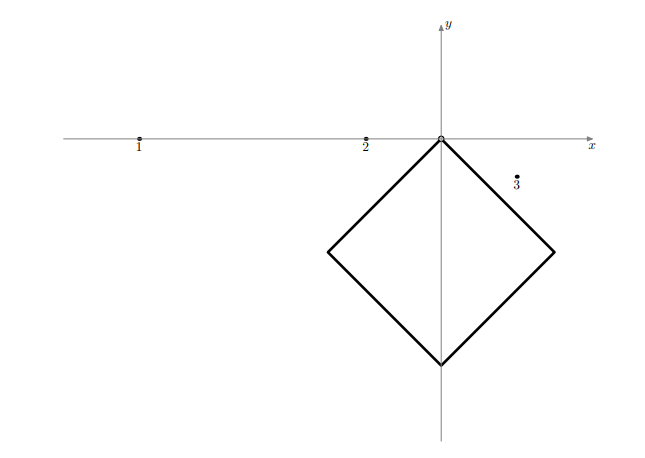
На рисунке выше изображен тест из примера. Прямоугольник показывает начальное положение пластины.
Точками показаны позиции, в которые Вася планирует забить гвоздь.
Гвоздь, забитый в первую точку, не мешает пластине поворачиваться.
Гвоздь, забитый во вторую точку, позволяет повернуть пластину на 45 гр. по часовой стрелке или на 225 гр. против часовой стрелки.
| |
![]()
|
4/
0
|
|
Темы:
Тернарный поиск
Вычислительная геометрия
Министерство дорожного транспорта решило построить себе новый офис. Поскольку министр регулярно выезжает с инспекцией наиболее важных трасс, было решено, что офис министерства не должен располагаться слишком далеко от них.
Наиболее важные трассы представляют собой прямые на плоскости. Министерство хочет выбрать такое расположение для своего офиса, чтобы максимум из расстояний от офиса до трасс был как можно меньше.
Требуется написать программу, которая по заданному расположению наиболее важных трасс определяет оптимальное расположение дома для офиса министерства дорожного транспорта.
Входные данные
Первая строка входного файла содержит одно целое число n — количество наиболее важных трасс (1 ≤ n ≤ 104 ).
Последующие n строк описывают трассы. Каждая трасса описывается четырьмя целыми числами x1, y1, x2 и y2 и представляет собой прямую, проходящую через точки (x1, y1) и (x2, y2) . Координаты заданных точек не превышают по модулю 104. Точки (x1 , y1) и (x2 , y2) ни для какой прямой не совпадают.
Выходные данные
Выходной файл должен содержать два разделенных пробелом вещественных числа: координаты точки, в которой следует построить офис министерства дорожного транспорта. Координаты по модулю не должны превышать 109, гарантируется, что хотя бы один такой ответ существует. Если оптимальных ответов несколько, необходимо выведите любой из них.
Ответ должен иметь абсолютную или относительную погрешность не более 10−6, что означает следующее. Пусть максимальное расстояние от выведенной точки до некоторой трассы равно x, а в правильном ответе оно равно y. Ответ будет засчитан, если значение выражения | x − y | / max(1, |y| ) не превышает 10−6.
| Ввод |
Вывод |
|
4
0 0 0 1
0 0 1 0
1 1 2 1
1 1 1 2
|
0.5000000004656613 0.4999999995343387 |
|
7
376 -9811 376 -4207
6930 -3493 6930 -8337
1963 -251 1963 -5008
-1055 9990 -684 9990
3775 -348 3775 1336
7706 -2550 7706 -8412
-9589 8339 -4875 8339
|
4040.9996151750674 12003.999615175067 |
Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2011, 2 день, Задача D
| |
![]()
|
19/
1
|
|
Темы:
Динамическое программирование
Вычислительная геометрия
Структуры данных
В коровий кёрлинг вовлечены две команды, каждая из которых двигает N тяжёлых камней (3 <= N <= 50,000) по льду. В конце игры имеется 2N камней на льду, каждый из которых расположен в различной точке
плоскости.
Подсчёт очков в коровьем кёрлинге ведётся следующим образом:
Камень считается «захваченным», если он содержится внутри треугольника, по углам которого находятся камни противника (камень, который находится на границе такого треугольника, также считается захваченным). Счёт команды есть количество камней команды противника, которые «захвачены».
Вычислите финальный счёт матча по коровьему кёрлингу, по заданному расположению всех камней.
INPUT FORMAT:
* Строка 1: Целое число N.
* Строки 2..1+N: Каждая строка содержит 2 целых числа, указывающих x и y координаты камня команды A (каждая координата лежит в диапазоне -40,000 .. +40,000).
* Строки 2+N..1+2N: Каждая строка содержит 2 целых числа, указывающих x и y координаты камня команды B (каждая координата лежит в диапазоне -40,000 .. +40,000).
OUTPUT FORMAT:
* Строка 1: Два разделённых пробелом целых числа, представляющих счета команд A и B
SAMPLE:
| Ввод |
Вывод |
4
0 0
0 2
2 0
2 2
1 1
1 10
-10 3
10 3 |
1 2 |
INPUT DETAILS:
У каждой команды по 4 камня.
Команда A имеет камни (0,0), (0,2), (2,0), (2,2).
Команда B имеет камни (1,1), (1,10), (-10,3), (10,3).
OUTPUT DETAILS:
Команда A захватила камень противника в точке (1,1).
Команда B захватила камни противника в точках (0,2) и (2,2).
| |
![]()
|
/
|
|
Темы:
Вычислительная геометрия
Фермер Джон нуждается в вашей помощи. Он решил построить изгородь в форме прямой, чтобы ограничить движение своих коров. Он рассматривает несколько вариантов размещения изгороди и с вашей помощью хочет определить наиболее подходящий. Подходящим считается вариант, когда все коровы находятся по одну сторону изгороди. Изгородь не считается подходящей, если хоть одна корова расположена на изгороди. ФД будет задавать вам вопросы про варианты изгороди, на которые вы должны отвечать YES, если изгородь подходит и NO, в противном случае.
Кроме того, ФД может добавить новых коров в стадо. С того момента, как корова добавлена, она должна быть по одну сторону от изгороди со всеми другими коровами.
Входные данные
Первая строка ввода содержит N (1 <= N <= 100000) и Q (1 <= Q <= 100000) разделённые одним пробелом. Это, соответственно, начальное количество коров в стаде и количество запросов.
Следующие N строк описывают начальное положение стада. Каждая строка содержит два целых числа x и x (разделённые пробелом), представляющие позицию очередной коровы.
Оставшиеся Q строк содержат запросы, либо добавляющие новую корову в стадо, либо проверяющие изгородь на применимость. Строка вида 1 x y означает, что новая корова добавляется в стадо на позицию x y. Строка вида 2 A B C означает, что ФД хочет проверить изгородь, описываемую прямой Ax+By=C.
Все позиции коров уникальны (-109 <= x, x <= 109). Кроме того, -109 <= A, B <= 109 и -1018 <= C <= 1018. Никогда не будет изгороди с A = B = 0.
Выходные данные
Для каждой изгороди выведите YES, если она подходит и NO, в противном случае.
| Ввод |
Вывод |
|
3 4
0 0
0 1
1 0
2 2 2 3
1 1 1
2 2 2 3
2 0 1 1
|
YES
NO
NO
|
Прямая 2x + 2y = 3 оставляет начальные 3 коровы по одну сторону. Однако корова (1,1) на другой стороне, поэтому после её добавления такая изгородь уже не подходит. Прямая Y=1 не подходит, поскольку коровы (0,1) и (1,1) находятся на ней.
Предупреждение: ввод-вывод для этой задачи очень большой. В С++ можно использовать scanf или ios_base::sync_with_stdio(false). В Java надо не использовать java.util.Scanner. Не делайте flush вывода (например? используя std::endl) после каждого запроса.
| |
![]()
|
1/
0
|
|
Темы:
Вычислительная геометрия
Новый градоначальник города Глупова решил с целью пополнения бюджета и экономии горючего провести кампанию борьбы с левым уклоном и левыми рейсами. Для этого он запретил водителям выполнять левые повороты, установив штраф за каждый поворот налево в размере одного миллиона (разворот поворотом налево не считается).
От тяжелого прошлого Глупову достались улицы, которые могут пересекаться под любыми углами. Градоначальник приказал установить компьютерную систему тотальной слежки, которая следит за каждым автомобилем, записывая его координаты каждый раз, когда тот меняет направление движения (включая начальную и конечную точки пути).
Требуется написать программу, вычисляющую по записанной последовательности координат автомобиля штраф, который должен быть взыскан с водителя.
Входные данные
В первой строке вводится целое число N - количество записанных пар координат (\(1 <= N <= 1000\)). В каждой из следующих N строк записана очередная из этих пар (вещественные числа).
Выходные данные
Выведите суммарный штраф водителя в миллионах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
0 0
1 0
1 1
2 1
|
1 |
| |
![]()
|
906/
196
|
|
Темы:
Вычислительная геометрия
Фрекен Бок находится в точке \(A(x_a, y_a)\) и, глядя прямо на Малыша, стоящего в точке \(B(x_b, y_b)\) задает вопрос: «В каком ухе у меня жужжит?». Естественно, у грозной домоправительницы жужжит в ухе, потому что в точке \(C(x_c, y_c)\) завис Карлсон со включенным мотором. Определите, какой ответ Малыша будет правильным.
Входные данные
С клавиатуры вводятся координаты точек A, B и С. Исходные данные являются целыми числами, по модулю не превышающими 1000.
Выходные данные
Выведите слово LEFT (заглавными буквами), если у домоправительницы жужжит в левом ухе, RIGHT – если в правом, BOTH – если жужжание и в левом и в правом одинаково.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
0 0 1 0 0 1 |
LEFT |
| |
![]()
|
819/
353
|
|
Темы:
Вычислительная геометрия
Входные данные
Шесть чисел – координаты точки и координаты начала и конца вектора.
Выходные данные
Одна строка “ YES”, если точка принадлежит лучу, определяемому вектором, и “ NO” в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 0 4 2 4 5 |
NO |
| |
![]()
|
2068/
559
|
|
Темы:
Вычислительная геометрия
Элементарная геометрия
Входные данные
Шесть чисел – координаты трёх вершин треугольника.
Выходные данные
Одно число – величина площади треугольника.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1 2 4 3 2 |
2.50000 |
| |
![]()
|
1926/
659
|
Темы:
Вычислительная геометрия
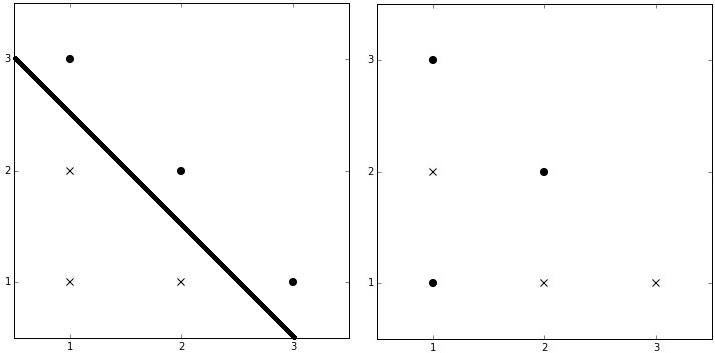
В машинном обучении часто возникает задача линейной классификации объектов, когда классы объектов разделяются между собой линейной поверхностью. Например, у нас есть информация о количестве дней с момента регистрации аккаунта в социальной сети и количество отправленных сообщений за последний
день, а также информация о том, является ли этот аккаунт спам-ботом. Возраст аккаунта мы можем взять за X координату точки, а количество сообщений за Y
коордианату. Задача классификации состоит в том, чтобы провести какую-либо прямую так, чтобы объекты одного типа находились по одну сторону этой прямой, а объекты другого типа по другую.
При наличии такой прямой мы сможем пронозировать тип даже незнакомого объекта по известному возрасту аккаунта и количеству отправленных сообщений в зависимости от того, с какой стороны от прямой оказался объект. Естественно, в реальных данных могут быть ошибки измерений или необычные объекты и провести такую прямую не всегда возможно, потому что, например, объект первого типа может случйно попасть в скопление объектов второго типа и отделить его прямой невозможно.
Вам необходимо по информации о параметрах и типе объектов определить, существует ли прямая, которая однозначно разделеят классы объектов. Прямая не должна проходить ни через один объект.
Формат входных данных
В этой задаче входной файл содержит несколько тестовых блоков.
В первой строке задано число T количество тестовых блоков (1 <= T <= 100).
Каждый тестовый блок состоит из числа N количество описанных объектов (1 <= N <= 2000).
В следующих N строках содержится описания объектов, состоящие из трех целых чисел X, Y , Type (0 <= X, Y <= 107 , 0 <= Type <= 1).
Формат выходных данных
Выведите T слов "YES" или "NO" по одному в строке для каждого из тестовых блоков. "YES" необходимо выводить если разделение на классы возможно, "NO" если невозможно.
Система оценки
Решения, верно работающие при T <= 10, N <= 100, будут набирать не менее половины баллов.
|
Ввод |
Вывод |
2
6
1 1 1
1 2 1
1 3 0
2 1 1
2 2 0
3 1 0
6
1 3 0
2 2 0
1 2 1
3 1 1
2 1 1
1 1 0 |
YES
NO |
| |
![]()
|
26/
2
|
|
Темы:
Вычислительная геометрия
На протяжении многих лет Вася работает программистом в одной очень большой и очень из- вестной компании. Эта компания обеспечивает своих сотрудников всем необходимым для приятной и плодотворной работы: бесплатными обедами, транспортом от дома до места работы и многим, многим другим. И вот в один прекрасный солнечный день Вася понял, что ему очень наскучил вид из окна его офиса, и ему нужно, чтобы за окном было что-то новое и прекрасное. А что может быть лучше чудесного горного пейзажа? Придя к этой мысли, Вася попросил своего менеджера подобрать себе новый офис с красивым видом на горы.
В той местности, где располагается офис Васи, каждая гора принадлежит некоторой горной цепи. Так как Васе хочется, чтобы вид из окна его офиса был идеальным, то он попросил подобрать себе такой офис, чтобы никакие две горные цепи, видимые из окна, не пересекались. Менеджер Васи нашел прекрасный новый офис, из которого видно N горных цепей, но он никак не может определить, понравится ли Васе вид из окна этого офиса. Помогите ему!
Более формально, вид из окна офиса представляет собой набор горных цепей, пронумерованных от 1 до N, где горная цепь с номером i представляет собой ломаную на плоскости из li звеньев с вершинами в точках (xi,j , yi,j ), причем для любых i, j выполнено xi,j < xi,j+1.
Кроме этого, окно в офисе имеет фиксированную ширину, поэтому все горные цепи начинаются и заканчиваются на одной вертикали, то есть существуют такие числа A и B, что для любого номера i горной цепи выполнено xi,0 = A, xi,li = B.
Отметим, что из определения горной цепи следует, что для любого значения абсциссы A <= x <= B на ломаной с номером i существует единственная точка (x, yi(x)) с этим значением абсциссы, при- надлежащая этой ломаной. Будем говорить, что горная цепь i находится строго выше горной цепи j в точке x, если выполнено строгое неравенство yi(x) > yj (x).
Естественно считать, что цепь под номером i пересекается с цепью под номером j, если су- ществуют такие два значения абсциссы x1, x2, что цепь i находится строго выше цепи j в точке x1, но при этом цепь j находится строго выше цепи i в точке x2, то есть выполнены неравенства yi(x1) > yj (x1) и yj (x2) > yi(x2). Обратите внимание на поясняющие рисунки, расположенные в примечании к задаче.
Вам необходимо определить, подойдет ли подобранный офис Васе, и, если нет, то найти любую пару пересекающихся горных цепей.
Формат входных данных
В первой строке входных данных через пробел идут два целых числа: A и B (−109<=A < B<=109 ).
Во второй строке входных данных находится единственное число N — количество горных цепей, видимых из окна подобранного менеджером Васи офиса (1 <= N <= 100 000).
Далее следуют описания N горных цепей. В первой строке i-го описания содержится число li => 1 — количество звеньев ломаной, из которых состоит соответствующая горная цепь. В следую- щих li + 1 строках описания содержатся два целых числа — координаты (xi,j , yi,j ) вершин ломаной (0 <= j <= li). Суммарное число звеньев всех ломаных не превосходит 200 000.
Гарантируется, что для каждой горной цепи вершины соответствующей ей ломаной идут во входных данных в порядке возрастания абсциссы, причем для любого i выполнено xi,0 = A, xi,li = B.
Формат выходных данных
Если же офис подходит Васе, то есть никакие две горные цепи из входных данных не пересека- ются, в единственной строке выходных данных выведите слово "Yes" (без кавычек).
Иначе выведите в первой строке слово "No" (без кавычек), а на следующей строке выведите два числа — номера двух пересекающихся горных цепей. Горные цепи нумеруются согласно их появлению во входных данных, начиная с 1.
Примеры
| Ввод |
Вывод |
-3 3
2
1
-3 2
3 1
2
-3 2
0 4
3 2 |
Yes |
0 4
2
3
0 3
1 3
3 1
4 1
1
0 2
4 2 |
No
1 2 |
Замечание
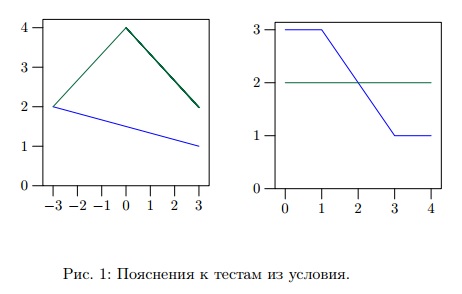
Напоминаем, что абсциссой точки называется её x-координата, а ординатой — её y-координата. В первом примере хотя ломаные и касаются друг друга в точке (−3, 2), но, согласно данному выше определению, они не пересекаются. Во втором примере в точке x1 = 1 одна ломаная выше другой, а в точке x2 = 3 — наоборот, то есть горные цепи пересекаются.
| |
![]()
|
25/
1
|
|
Темы:
Вычислительная геометрия
Свершилось чудо! Наконец-то вышел долгожданный Half-Life 3, о котором мечтали миллионы людей по всему миру! Вася тоже с нетерпением ждал продолжения легендарной серии, и даже не ел в школьной столовой целый месяц, чтобы ему хватило на покупку этого шедевра! Единственная проблема, которая стоит у него на пути - огромное домашнее задание по алгебре. В классе он прошёл новую тему - прямые, и теперь ему нужно сделать аж N задач на построение прямой через 2 точки. Но ведь так хочется поиграть, а на следующий день рассказывать друзьям, какой же там классный графон... Поэтому он попросил Вас, своего друга, помочь ему.
Входные данные
В первой строке вводятся координаты первой точки (X1, Y1), (\(-50 <= X_1, Y_1 <= 50\)).
Во второй строке вводятся координаты второй точки (X2, Y2), (\(-50 <= X_2, Y_2 <= 50\)).
Выходные данные
В единственной строке выведите подряд 3 целых числа: коэффициенты a, b, c уравнения прямой.
Примечание: если у вас не заходит задача, но вы уверены, что всё правильно - попробуйте умножить все коэффициенты на -1. Задача предполагает, что вы использовали формулы, взятые с лекции/теории.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
-1 -1
1 1
|
-2 2 0 |
| |
![]()
|
135/
70
|
|
Темы:
Вычислительная геометрия
В плоской стране наступила очередная зима, и нужно срочно переводиться на зимнее время! Проблема в том, что стрелка городских часов (единственная, кстати), находящихся в начале координат, очень-очень тяжёлая, и поэтому рабочие хотят узнать, в какую сторону крутить стрелку будет быстрее. Чтобы упростить вам задачу, они уже посчитали, куда указывает стрелка и куда она должна указывать. Помогите им!
Входные данные
В первой строке задаётся точка, куда указывает стрелка. Она задаётся координатами X1 и Y1 (\(-10 <= X_1, Y_1 <= 10\)).
Во второй строке задаётся точка, куда должна указывать стрелка. Она задаётся координатами X2 и Y2 (\(-10 <= X2, Y2 <= 10\)).
Координаты задаются вещественным типом.
Выходные данные
В единственной строке выведите "Clockwise", если стрелку нужно крутить по часовой стрелке, "Counter-clockwise", если её нужно крутить против часовой стрелки, и "Doesn't matter", если это займёт одинаковое время, в какую сторону её бы не крутили. Выводить фразы следует без кавычек.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 0
-1 1
|
Counter-clockwise |
| |
![]()
|
876/
230
|
|