| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Идеи
Многоугольники. Выпуклые оболочки
Недавно в город приехал известный цирк. Всего в этом цирке \(n\) акробатов, и в этот раз в честь проведения СПбКОШП 2022 они подготовили особенный номер.
Известно, что \(i\)-й акробат имеет рост \(a_i\) и вес \(b_i\). Любые три акробата могут собраться вместе и показать необычный трюк. Если трюк показывают акробаты с номерами \(i\), \(j\) и \(k\), то эффектность трюка оценивается как \(a_i b_j + a_j b_k + a_k b_i\).
Тренер акробатов считает упорядоченную тройку акробатов \((i, j, k)\) хорошей, если эффектность их трюка будет не меньше, чем если они расположатся в обратном порядке \((k, j, i)\).
Для номера тренер хочет расположить всех \(n\) акробатов в один ряд так, чтобы любая тройка подряд идущих акробатов была хорошей. Помогите ему с этой нелегкой задачей!
Формат входных данных
В первой строке ввода дано целое число \(n\) — количество акробатов в цирке (\(3 \leqslant n \leqslant 1000\)).
В \(i\)-й из следующих \(n\) строк через пробел даны целые числа \(a_i\) и \(b_i\) — рост и вес \(i\)-го акробата (\(1 \leqslant a_i, b_i \leqslant 10^9\)).
Формат входных данных
Выведите через пробел \(n\) различных целых чисел от \(1\) до \(n\) — номера акробатов в том порядке, в котором их стоит расположить в ряду.
| |
![]()
|
6/
3
|
|
Темы:
Многоугольники. Выпуклые оболочки
Фен шуй – это древняя китайская практика размещения предметов в пространстве для достижения гармонии. В ней говорится, что пол не должен быть пустым, поэтому Фил разместил на полу два одинаковых круглых ковра (по фен шуй надо избегать прямых линий и острых углов).
К сожалению, ими нельзя покрыть пол комнаты полностью, так как она имеет форму выпуклого многоугольника. Фил хочет минимизировать непокрытую часть пола, располагая ковры оптимальным образом.
Помогите ему расположить два ковра в комнате так, чтобы общая покрытая площадь была максимальна. Ковры можно накладывать друг на друга, но их нельзя загибать и резать.
.png)
Входные данные
Первая строка входных данных содержит два целых числа n и r — число углов в комнате (3 ≤ n ≤ 100) и радиус ковров (1 ≤ r ≤ 1000, оба ковра имею один и тот же радиус). Следующие n строк содержат по два числа xi и yi — координаты i-го угла \((–1000 \le x_i; y_i \le 1000)\) . Углы описаны в порядке обхода комнаты по часовой стрелке. Координаты углов различны и соседние стены не коллинеарны.
Выходные данные
Выведите \(x_1, y_1, x_2, y_2\), где(\(x_1, y_1\)) и (\(x_2, y_2\)) обозначаю центры ковров. Координаты должны иметь точность не менее 4 цифр после точки. Выведите любое оптимальное расположение. Входные данные гарантируют, что решение существует (Фил не стал бы покупать ковер, который не помещается в комнату).
| |
![]()
|
1/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
Есть замок — точка (0,0). Замок окружен несколькими непересекающимися заборами, каждый представляет из себя выпуклый многоугольник.
Есть также М захватчиков, известны их координаты. Захватчики не умеют перелезать через заборы. Захватчика будем считать опасным, если он находится внутри внешнего забора. Требуется вычислить суммарную площадь области, куда опасные захватчики могут добраться без пересечения заборов.
Если захватчик находится на границе забора, то считается, что он может добраться до той части, которая находится внутри, и не может добраться до той, которая снаружи.
Входные данные
8 первой строке задано число N (1≤N≤100000). Далее следуют описания N заборов. Каждое описание начинается с числа K, далее следуют К строк, содержащих по два числа X и Y — координаты вершин (0≤X,Y≤2⋅106). Вершины каждого многоугольника перечисляются в порядке обхода против часовой стрелки. Гарантируется, что точка (0,0) лежит внутри каждого забора.
Далее следует число M (0≤M≤100000) — количество захватчиков. В следующих М строках заданы координаты захватчиков.
Суммарное число вершин во всех многоугольниках не превосходит 100000.
Все вводимые числа являются целыми.
Выходные данные
Выведите единственное число — общую захваченную площадь с шестью знаками после десятичной точки.
| |
![]()
|
11/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
На плоскости заданы N точек своими декартовыми координатами. Найти минимальный периметр многоугольника, содержащего все эти точки. Гарантируется, что искомый многоугольник имеет ненулевую площадь.
Входные данные
В первой строке находится число N, далее - N строк с парами координат. 3 <= N <= 1000, -10 000 <= xi, yi <= 10 000, все числа целые, все точки различны.
Выходные данные
Вывести одно число - длину периметра с одним знаком после запятой.
| |
![]()
|
2/
2
|
|
Темы:
Многоугольники. Выпуклые оболочки
Многоугольник на плоскости задан целочисленными координатами своих N вершин в декартовой системе координат. Требуется найти площадь многоугольника. Стороны многоугольника не соприкасаются (за исключением соседних - в вершинах) и не пересекаются.
Входные данные
В первой строке находится число N. В следующих N строках находятся пары чисел - координаты точек. Если соединить точки в данном порядке, а также первую и последнюю точки, получится заданный многоугольник. 3 <= N <= 50 000, координаты вершин целые и по модулю не превосходят 20 000.
Выходные данные
Вывести одно число - площадь многоугольника. Его следует округлить до ближайшего числа с одной цифрой после запятой.
| |
![]()
|
2/
2
|
|
Темы:
Многоугольники. Выпуклые оболочки
Сканирующая прямая
Множество на плоскости называется выпуклым, если вместе с любыми двумя точками оно содержит также и отрезок, соединяющий эти точки. Минимальное по включению выпуклое множество, содержащее заданное множество точек \(X\), называется выпуклой оболочкой множества \(X\).
В этой задаче вам требуется найти выпуклую оболочку множества точек, принадлежащих заданному набору углов.
Углом называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Эта точка называется вершиной угла.
На рисунке слева приведены два угла, на рисунке справа изображена их выпуклая оболочка.
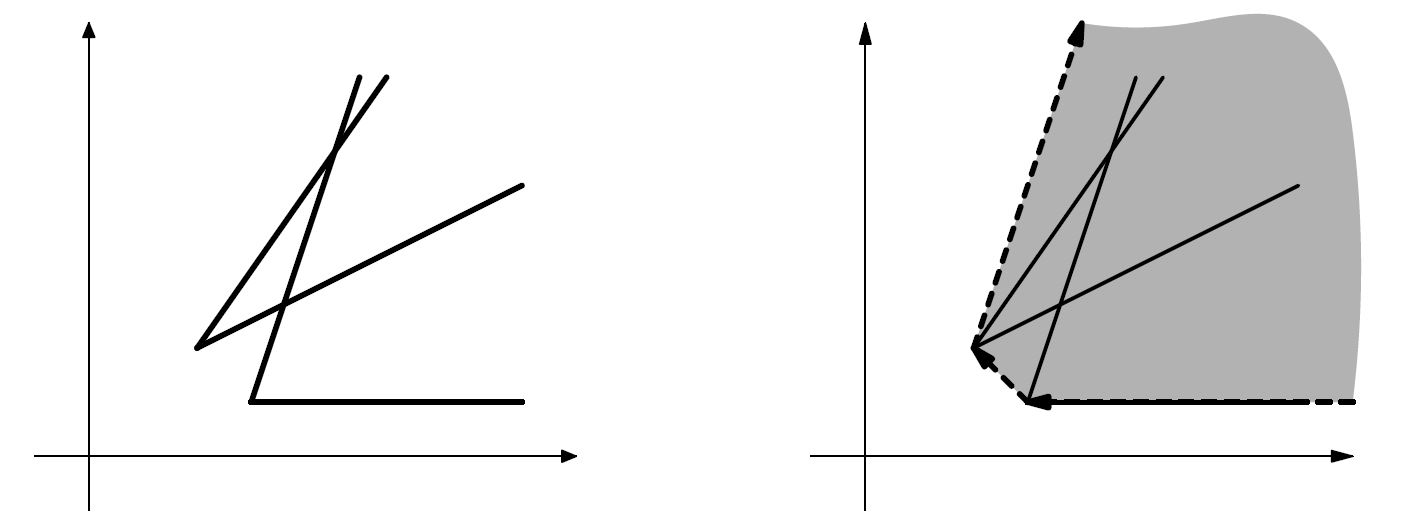
Формат входных данных
Первая строка содержит число \(n\) — количество углов (\(1 \le n \le 1000\)). Каждая из следующих \(n\) строк описывает углы. Каждый угол описывается координатами трех точек: вершины и двух отличных от вершины точек — по одной на каждом из лучей. Все координаты целые и не превышают \(10^4\) по абсолютной величине. Величина угла находится в диапазоне от 0 до 180 градусов, не включительно.
Формат выходных данных
Выведите границу выпуклой оболочки в виде последовательности направленных лучей, прямых и отрезков. Никакие два объекта в выходном файле не должны лежать на одной прямой. Все отрезки должны иметь длину больше нуля. Объекты должны быть перечислены в таком порядке, чтобы начало каждого следующего совпадало с концом предыдущего. Все числа должны быть целыми и не превосходить \(10^5\) по абсолютной величине. При проходе вдоль описанной границы выпуклая оболочка углов должна быть справа.
На первой строке выведите \(l\) — количество объектов в ответе. Следующие \(l\) строк должны содержать описание объектов. Объекты описываются следующим образом:
-
Отрезок: <<segment \(x_1\) \(y_1\) \(x_2\) \(y_2\)>>, где \((x_1, y_1)\) и \((x_2, y_2)\) — концы отрезка, отрезок считается направленным от \((x_1, y_1)\) к \((x_2, y_2)\).
-
Луч, направленный от начала: <<outray \(x_1\) \(y_1\) \(x_2\) \(y_2\)>>, где \((x_1, y_1)\) — начало луча, а \((x_2, y_2)\) — произвольная точка на луче, отличная от начала.
-
Луч, направленный к началу: <<inray \(x_1\) \(y_1\) \(x_2\) \(y_2\)>>, где \((x_2, y_2)\) — начало луча, а \((x_1, y_1)\) — произвольная точка на луче, отличная от начала.
-
Прямая: <<line \(x_1\) \(y_1\) \(x_2\) \(y_2\)>>, где \((x_1, y_1)\) и \((x_2, y_2)\) — две точки на прямой, причем при движении вдоль прямой в ее направлении точка \((x_1, y_1)\) следует ранее точки \((x_2, y_2)\).
Если выпуклой оболочкой является вся плоскость, то выведите \(l = 0\).
| |
![]()
|
1/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
Рассмотрим выпуклый многоугольник, вершины которого лежат в точках плоскости с целыми координатами. Требуется разбить его на треугольники с вершинами в точках с целыми координатами, каждый из которых имел бы площадь 1/2, либо выяснить, что это сделать невозможно.
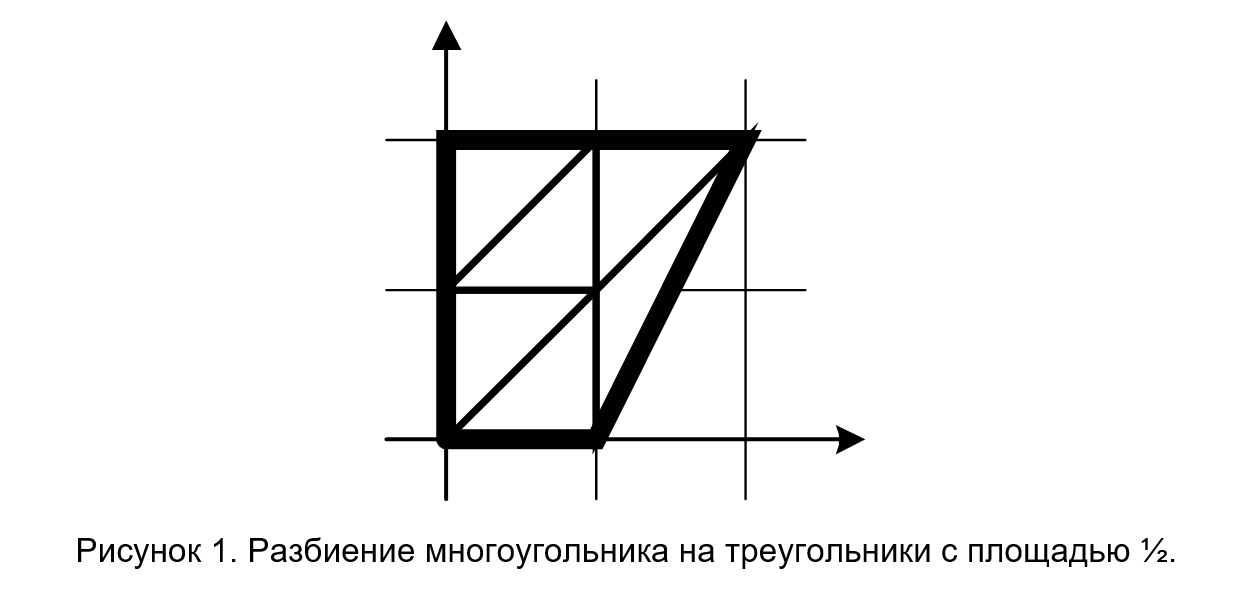
Входные данные
В первой строке вводится число N - количество вершин многоугольника (1 <= N <= 10). Следующие N строк содержат координаты вершин многоугольника в порядке обхода их по часовой стрелке. Все координаты - целые неотрицательные числа, не превышающие 10. Никакие три последовательные вершины многоугольника не лежат на одной прямой.
Выходные данные
Если выполнить разбиение указанным образом невозможно, выведите единственное число - 0. В противном случае выведите несколько строк, содержащих по 6 чисел каждая. Количество строк должно быть равно количеству треугольников в найденном разбиении. Числа в каждой строке должны представлять собой координаты вершин соответствующего треугольника - x1, y1, x2, y2, x3, y3. Площадь каждого треугольника должна быть 1/2. Порядок перечисления треугольников и вершин в каждом из треугольников может быть произвольным. Если допустимых разбиений несколько, выведите любое.
| |
![]()
|
1/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
Элементарная геометрия
Будем говорить, что для наблюдателя лес является дремучим, если из своего текущего положения наблюдатель видит только деревья. Вам дана карта леса и координаты точки, в которой находится наблюдатель. Требуется определить, кажется ли лес дремучим данному наблюдателю.
На карте леса все деревья изображаются кругами. При этом в лесу бывают сросшиеся деревья (изображения таких деревьев на карте пересекаются), также одно дерево может находиться внутри другого. Точка, в которой стоит наблюдатель, не лежит внутри или на границе ни одного из деревьев.
Входные данные
Cначала вводится целое число N - количество деревьев (1≤N≤50000). Затем идут два числа, задающих координаты наблюдателя. Затем идет N троек чисел, задающих деревья (первые два числа тройки задают координаты центра, а третье - радиус). Все координаты задаются точно и выражаются вещественными числами, по модулю не превосходящими 100000 и записанными не более чем с 2 знаками после десятичной точки.
Выходные данные
В первой строке выведите сообщение YES, если лес является дремучим, и NO - иначе. Во втором случае во вторую строку необходимо вывести координаты точки, глядя в направлении которой наблюдатель не видит деревьев (то есть луч, вдоль которого смотрит наблюдатель, не проходит внутри деревьев и не касается ни одного из деревьев). Координаты нужно вывести не менее, чем с 3 знаками после десятичной точки. Координаты не должны превышать 300000. Расстояние между выданной точкой и наблюдателем должно быть не меньше 1.
| |
![]()
|
3/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
На плоскости нарисовали прямоугольник, после чего его разрезали прямыми. Напишите программу, которая вычислит, сколько из полученных кусков исходного прямоугольника имеют треугольную форму.
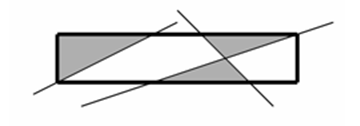
Входные данные
Сначала вводятся два положительных числа X, Y, задающих координаты правого верхнего угла прямоугольника. Прямоугольник расположен в системе координат так, что левый нижний его угол имеет координаты 0,0 и стороны параллельны осям координат.
Далее записано целое число N - количество разрезов (1≤N≤200). Далее описываются сами разрезы. Все разрезы делались вдоль прямых. Каждая прямая, соответствующая разрезу, задается тремя числами A, B, C такими, что все точки (x,y) этой прямой (и только они) удовлетворяют уравнению Ax+By+C=0 (при этом всегда A2+B2>0).
Все вводимые числа (кроме N) вещественные, заданы с двумя знаками после десятичной точки и не превышают 104. Никакие две прямые не совпадают между собой и не содержат сторон прямоугольника. Каждый разрез проходит через точки внутри исходного прямоугольника.
Выходные данные
Выведите одно целое число - количество частей исходного прямоугольника, имеющих треугольную форму.
| |
![]()
|
1/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
K членов Жюри Десятой Всероссийской олимпиады школьников по информатике решили отметить столь круглую годовщину в одном из лучших ресторанов на Невском проспекте. На десерт вниманию Жюри предложили торт, имеющий форму прямоугольной призмы с выпуклым N-угольником в основании. Жюри вооружается десертными ножами и собирается справедливо разделить торт на K частей равного объема. Ножами можно проводить прямые вертикальные разрезы от одной границы торта до другой; различные разрезы могут иметь общие точки лишь в своих концевых вершинах.
Напишите программу, помогающую членам Жюри построить требуемые K-1 разрезов.
Входные данные
В первой строке входных данных содержатся два целых числа K и N (1 <= K, N <= 50). Далее следуют N пар вещественных чисел - координаты последовательно расположенных вершин N-угольника.
Выходные данные
Каждый из K-1 разрезов в выходных данных должен быть представлен четверкой вещественных чисел с не менее чем 10 знаками после запятой - координатами концов соответствующего разреза. Все числа должны быть разделены пробелами и/или символами перевода строки.
| |
![]()
|
1/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
Даны N точек. Требуется построить круг минимального радиуса такой, чтобы этот круг целиком покрывал все точки (допустимо, чтобы некоторые точки лежали на границе круга).
Входные данные
Сначала вводится число N - количество точек, 3<=N<=100000. Далее идут N пар чисел, задающих координаты точек. Координаты - вещественные числа.
Выходные данные
Выведите три числа - координаты центра и радиус искомого круга. Если решений несколько, выведите любое из них.
| |
![]()
|
4/
3
|
|
Темы:
Многоугольники. Выпуклые оболочки
Задан многоугольник и точка. Нужно определить, лежит ли точка внутри этого многоугольника. В этой задаче многоугольник невыпуклый.
Входные данные
Сначала вводится число N (3<=N<=100). Далее идут N пар вещественных чисел, задающих координаты вершин многоугольника. Последние два вещественных числа задают координаты точки.
Выходные данные
Выведите сообщение YES, если точка лежит внутри многоугольника, или NO, если нет. Гарантируется, что точка не лежит на границе многоугольника.
| |
![]()
|
2/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
Задан многоугольник и точка. Нужно определить, лежит ли точка внутри этого многоугольника. В этой задаче многоугольник выпуклый.
Решите задачу быстрым методом
Входные данные
Сначала вводится число N (3<=N<=100). Далее идут N пар вещественных чисел, задающих координаты вершин многоугольника. Последние два вещественных числа задают координаты точки.
Выходные данные
Выведите сообщение YES, если точка лежит внутри многоугольника, или NO в противном случае. Гарантируется, что точка не лежит на границе многоугольника.
| |
![]()
|
3/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
На плоскости задан многоугольник координатами вершин в порядке их обхода. Многоугольник не обязательно выпуклый. Требуется найти его площадь.
Входные данные
Сначала вводится число N - количество вершин многоугольника (3<=N<=100), затем N пар целых чисел, задающих координаты его вершин.
Выходные данные
Выведите площадь многоугольника не меньше, чем с 3 знаками после десятичной точки.
| |
![]()
|
4/
4
|
|
Темы:
Многоугольники. Выпуклые оболочки
В саду растут деревья. У каждого есть цена и длина. Чтобы построить забор какой-то длины L, нужно срубить деревьев с суммарной длиной L или больше. Нужно, срубив некоторые деревья, построить забор вокруг оставшихся. При этом нужно потратить как можно меньше денег. Если таких способов несколько, нужно выбрать тот, в котором деревьев рубится меньше. Если и таких несколько, выведите любой. Деревья считаются имеющими нулевой радиус.
Входные данные
Во входном файле записано число деревьев N (2 <= N <= 14), а затем каждое дерево описано четырьмя числами xi, yi, vi, li - координаты (целые от -10000 до 10000), цена и длина (от 0 до 10000).
Выходные данные
В выходной файл выведите номера деревьев, которые необходимо срубить, а также излишек срубленного материала. Формат выходных данных - см. примеры выходных файлов.
| |
![]()
|
2/
0
|
|
Темы:
Динамическое программирование по профилю
Многоугольники. Выпуклые оболочки
Король Полигонии Трианг IV помешан на реформах. Чтобы войти в мировую историю, он решил провести территориальную реформу в своей стране. Страна Полигония имеет форму простого многоугольника, то есть ее граница не имеет самопересечений и самокасаний. В Полигонии большую роль играют внутренние диагонали — отрезки, соединяющие вершины государственной границы и полностью проходящие по территории страны, не касаясь границы. При этом форма Полигонии такова, что никакие две внутренние диагонали не лежат на одной прямой.
Вместо традиционного деления государства на административные округа король Трианг IV решил разделить свою страну на административные треугольники внутренними диагоналями. Для сокращения управляющего аппарата король повелел подготовить такой план деления страны, в котором количество административных треугольников будет минимальным.
Требуется написать программу, выполняющую деление Полигонии внутренними диагоналями на минимально возможное число административных треугольников.
Формат входных данных
В первой строке входных данных задается число N (3 ≤ N ≤ 20) — количество вершин многоугольника, образующего границу Полигонии. В следующих N строках находятся по 2 целых числа, по абсолютной величине не превосходящих 10 000 — координаты вершин в порядке обхода многоугольника против часовой стрелки. Гарантируется, что никакие три последовательные вершины многоугольника не лежат на одной прямой, и он не имеет самопересечений и самокасаний. Также гарантируется, что никакие две диагонали, содержащиеся внутри многоугольника, не лежат на одной прямой.
Формат выходных данных
В первую строку выведите наименьшее количество административных треугольников, на которое можно разбить Полигонию.
Во вторую строку выведите количество различных внутренних диагоналей K, с помощью которых можно произвести данное разбиение.
В каждую из следующих K строк выведите 4 целых числа — координаты начала и конца соответствующей диагонали разбиения, полностью лежащей внутри многоугольника и не проходящей по его границе.
Если искомых разбиений несколько, выведите любое из них.
Примеры
| № |
Входные данные |
Выходные данные |
Рисунок к тесту |
| 1 |
4
0 0
1 0
1 1
0 1 |
2
1
1 1 0 0 |
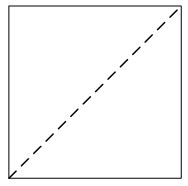 |
| 2 |
10
-6 0
0 2
6 0
3 3
6 4
2 4
0 6
-2 4
-6 4
-3 3 |
4
3
2 4 -2 4
0 2 3 3
-3 3 0 2 |
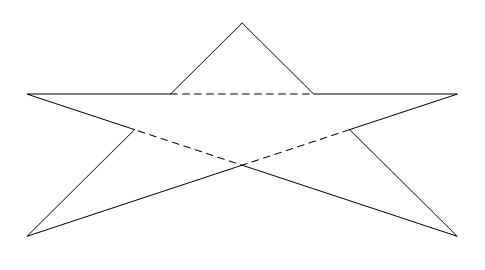 |
| |
![]()
|
4/
1
|
|
Темы:
Многоугольники. Выпуклые оболочки
На плоскости даны N точек. Вам требуется построить выпуклую оболочку данного множества точек. Выведите два числа: периметр и площадь.
Входные данные
Первая строка содержит количество точек N, 1≤N≤10000. Каждая из последующих N строк содержит два целых числа – координаты xi и yi. Все числа по модулю не превосходят 104.
Выходные данные
Вывести два числа: периметр и площадь выпуклой оболочки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
0 0
3 4
3 1
6 0 |
16.0000000000
12.0000000000 |
| |
![]()
|
27/
3
|
|
Темы:
Многоугольники. Выпуклые оболочки
Входные данные
В первой строке вводятся три целых числа – N (3≤N≤100000) и координаты точки. Далее в N строках задается по паре целых чисел – координаты очередной вершины простого многоугольника в порядке обхода по или против часовой стрелки.
Выходные данные
Выведите одну строку: “YES”, если заданная точка содержится в приведённом многоугольнике или на его границе, и “NO” в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 2 3
1 1
10 2
2 8 |
YES |
| |
![]()
|
484/
48
|
|
Темы:
Многоугольники. Выпуклые оболочки
Входные данные
В первой строке вводится одно число N (3≤N≤100000). Далее в N строках задается по паре чисел – координаты очередной вершины простого многоугольника в порядке обхода по или против часовой стрелки.
Выходные данные
Выведите одну строку: “YES”, если приведённый многоугольник является выпуклым, и “NO” в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 0
0 1
1 0 |
YES |
| 2 |
6
0 0
0 2
1 2
1 1
2 1
2 0 |
NO |
| |
![]()
|
957/
165
|
|
Темы:
Элементарная геометрия
НОД и алгоритм Евклида
Многоугольники. Выпуклые оболочки
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Формат входных данных
В первой строке содержится N (3 ≤N ≤1000) – число вершин многоугольника. В последующих N строках идут координаты (Xi, Yi) вершин многоугольника в порядке обхода по часовой стрелке. Xi и Yi - целые числа, по модулю не превосходящие 1000000.
Формат выходных данных
Вывести одно число – искомое число точек.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
-1 -1
-1 1
1 1
1 -1 |
1 |
| 2 |
3
0 0
0 2
2 0
|
0 |
| |
![]()
|
12/
4
|
|