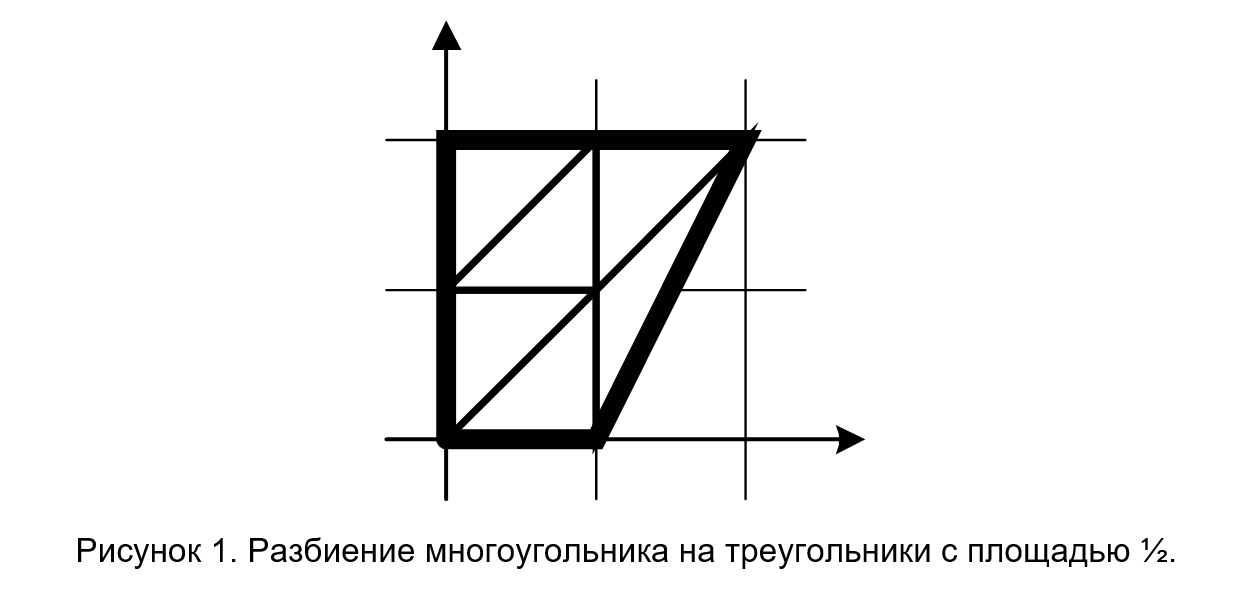
Рассмотрим выпуклый многоугольник, вершины которого лежат в точках плоскости с целыми координатами. Требуется разбить его на треугольники с вершинами в точках с целыми координатами, каждый из которых имел бы площадь 1/2, либо выяснить, что это сделать невозможно.
 Входные данные
Входные данные
В первой строке вводится число N - количество вершин многоугольника (1 <= N <= 10). Следующие N строк содержат координаты вершин многоугольника в порядке обхода их по часовой стрелке. Все координаты - целые неотрицательные числа, не превышающие 10. Никакие три последовательные вершины многоугольника не лежат на одной прямой.
Выходные данные
Если выполнить разбиение указанным образом невозможно, выведите единственное число - 0. В противном случае выведите несколько строк, содержащих по 6 чисел каждая. Количество строк должно быть равно количеству треугольников в найденном разбиении. Числа в каждой строке должны представлять собой координаты вершин соответствующего треугольника - x
1, y
1, x
2, y
2, x
3, y
3. Площадь каждого треугольника должна быть 1/2. Порядок перечисления треугольников и вершин в каждом из треугольников может быть произвольным. Если допустимых разбиений несколько, выведите любое.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
0 0
0 2
2 2
1 0
|
2 2 0 1 1 2
0 1 0 2 1 2
0 0 0 1 1 1
0 1 2 2 1 1
2 2 1 0 1 1
1 0 0 0 1 1
|