Элементарная геометрия

Дан набор точек. Напишите программу, которая считает количество соседей у заданной точки в радиусе eps

Формат входных данных
Первая строка: n eps — количество точек и радиус (n - натуральное, не превышает 100 , eps - вещественное)
Следующие n строк: x y — координаты точек (целые числа, по модулю не превышают 100)
Последняя строка: qx qy — точка запроса (целые числа, по модулю не превышают 100). 
Гарантируется, что заданная точка находится в заданном наборе точек.

Формат выходных данных
Одно число — количество соседей (не считая саму точку)

Город имеет форму круга радиуса R с центром в точке (0,0).
Сеть метро состоит из N линий метро (часть линий или все проходят через город).
Линия метро - ломаная из отрезков прямых, вершины которых имеют целочисленные координаты. Линия метро не имеет самопересечений и может быть замкнутой. Во всех точках с целочисленными координатами, через которые проходят линии метро расположены станции метро .
Для каждой точки с целочисленными координатами определим параметр вес вершины. Вес вершины — это количество станций метро, расстояние до которых не более 1 (длины клетки).
Город разбит на кварталы. Квартал — это единичная клетка с целочисленными координатами вершин, хотя бы одна из которых находящаяся строго внутри города.
Для каждого квартала определим параметр доступность. Доступность квартала равна сумме весов вершин квартала (вершина квартала может быть вне города)
Найдите значение "доступности" для каждого квартала. Для каждой полученной "доступности" определите число кварталов, имеющих эту доступность.
Входные данные
В первой строке заданы значения R, N (4<R<201, 0<N<1001)
В следующих N строках заданы описания линий метро.
Каждая линия описывается следующим образом:
первое число в строке M равно количеству вершин ломаной, далее даны координаты вершин (по два числа на вершину).
Замкнутые ломаные определяются тем, что координаты начальной и конечной вершины совпадают.
Выходные данные
В первой строке выведите число K - количество различных значений "доступности" (включая нулевую).
В следующих K строках выведите по два числа - значение "доступности" и число кварталов, имеющих такое значение "доступности"

Примеры:

 

 

№	Входные данные	Выходные данные	Примечание
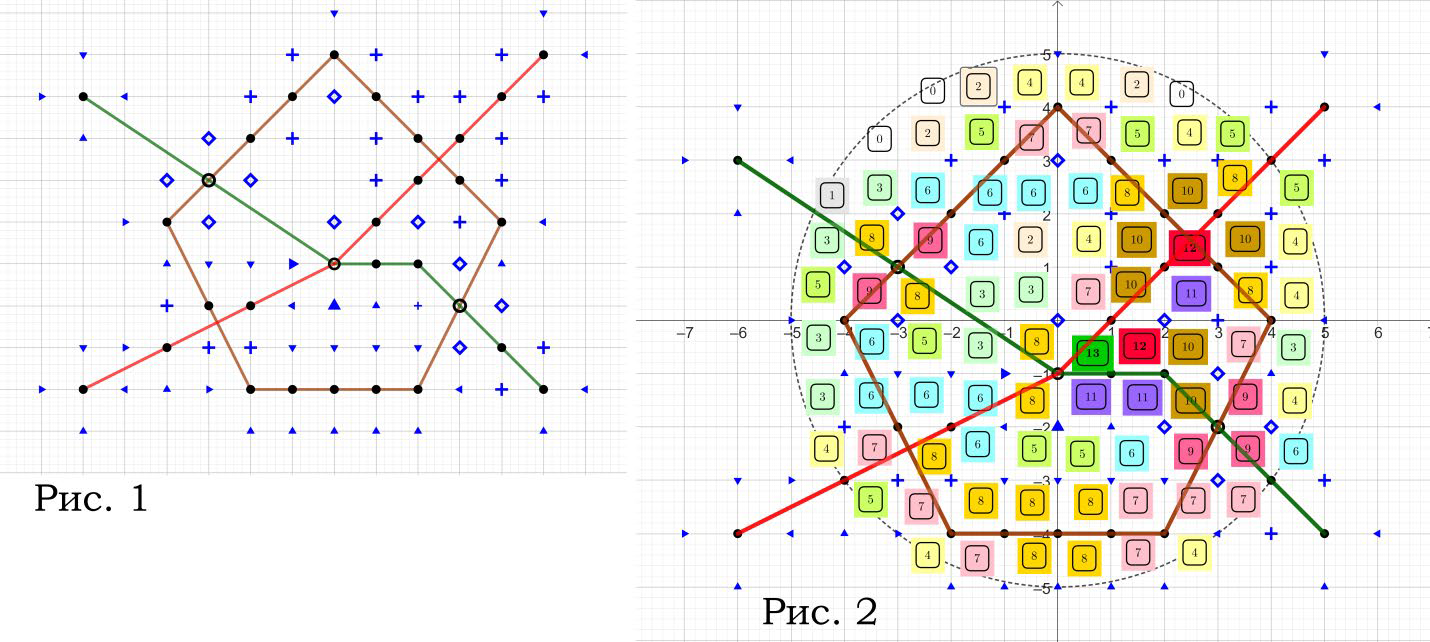
1	5 3 6 2 -4 -2 -4 -4 0 0 4 4 0 2 -4 4 -6 3 0 -1 2 -1 5 -4 3 5 4 0 -1 -6 -4	14 0 3 1 1 2 4 3 8 4 10 5 9 6 12 7 11 8 13 9 5 10 6 11 3 12 2 13 1	Город (рис. 1,2) расположен в круге радиуса 5 с центром в точке (0,0). Сеть метро состоит из 6 линий метро (2 радиальных, 1 кольцевая): 6 2 -4 -2 -4 -4 0 0 4 4 0 2 -4 - кольцевая линия из 5 звеньев, 16 станций 4 -6 3 0 -1 2 -1 5 -4 - радиальная линия из 3 звеньев, 8 станций 3 5 4 0 -1 -6 -4 - радиальная линия из 2 звеньев, 9 станций Есть три пересадки ( в вершинах (-3,1), (0,-1), (3,-2)) На рис.1 отмечены вершины, которые не являются станциями и имеют не нулевой вес (треугольник - вес 1, крестик - вес 2, ромб - вес 3) На рис.2 для всех городских кварталов указано значение параметра доступности квартала.

 

Саша и Маша живут в разных домах одного района. Их дома находятся возле пруда в форме квадрата. Однажды глава района предложил жителям нарисовать тропинки, которые они хотели бы видеть в своём районе, чтобы в дальнейшем проложить их. Потому ребята решили рассчитать самый короткий маршрут, который может быть, чтобы пройти от одного дома к другому. На изображении ниже представлен вариант расположения пруда и двух домов ребят (зелёная точка и оранжевая). Требуется рассчитать, какое самое кратчайшее расстояние требуется им преодолеть, чтобы оказаться друг у друга в гостях.


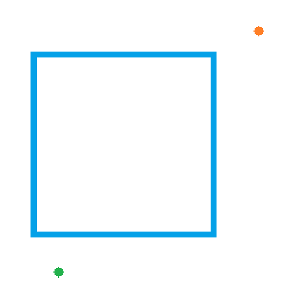
Примечание:

• дома могут находиться как по разные стороны пруда, так и поодну;
• требуется рассчитать ответ с точностью до десятых (если ответполучился целый, то выводить всегда после запятой один знак);
• передвигаться можно только по прямым, но не дугам;
• стороны пруда всегда параллельны осям OX и OY;
• точки, обозначающие дома могут лежать на границе пруда, и передвигать по границе пруда разрешено. 

Формат входных данных
На первой строке подаются параметры пруда через пробел a, x1, y1 (1 <= a <= 1000; -1000 <= x1,y1 <= 1000), где x1,y1 – координаты левого верхнего угла пруда.
На второй строке подаются координаты дома Маши в виде точки xm, ym (-1000 <= xm, ym <= 1000).
На третьей строке подаются координаты дома Саши в виде точки xs, ys (-1000 <= xs, ys <= 1000).
Все числа - целые.
Формат выходных данных
Выведите на одной строке самое кратчайшее расстояние, которое можно пройти от дома Маши к дому Саши. Ответ представляет собой всегда вещественное число с одним знаком после запятой. Если ответ получился больше, то округлить до одного знака после запятой (было 4.5764, стало 4.6).

 

Тимофею на день рождения родители подарили металлоискатель. Естественно, наутро мальчик отправился на поиски клада. Он предположил, что когда-то давно кто-то мог обронить золотую монету на древней прямой дороге и для облегчения поиска придумал систему координат. Ось абсцисс OX направлена вдоль дороги, а ось ординат OY направлена вверх.
Устройство работает следующим образом: на его индикаторе выставляется натуральное число r и если ровно на этом расстоянии имеется золотой предмет, то загорается зелёная лампочка.
Сначала юный кладоискатель выставил число r1 в точке x = 0, затем отошёл в точку с абсциссой x = a и выставил число r2, как показано на рисунке. Новичкам везёт, оба раза загорелась зелёная лампочка. Определите координаты потерянной когда-то давно золотой монетки.

Формат входных данных
Программа получает на вход три целых числа a, r1 и r2, записанных в отдельных строках (1 ≤ a, r₁, r₂ ≤ 10⁹ ).
Формат выходных данных
Выведите в двух строках два числа – координаты сокровища (сначала — абсциссу, потом — ординату). Значение ординаты должно быть не положительным (монетка не может висеть в воздухе). Гарантируется, что входные данные таковы, что ответ существует и обе координаты монеты будут целыми числами.

Замечание
Рисунок соответствует примеру из условия.

Даны:

1.  круг, заданный тремя числами  (r, x0, y0) - радиус и координаты центра окружности,
2.  прямоугольник, заданный четырьмя числами (x1, y1, x2, y2), где (x1, y1) — это координаты нижнего левого угла, а (x2, y2) — это координаты верхнего правого угла прямоугольника. Стороны прямоугольника параллельны осям координат.

Напишите программу, которая выводит true, если круг и прямоугольник пересекаются, иначе - false. Другими словами, проверьте, существует ли хотя бы одна точка (xi, yi), которая принадлежит как кругу, так и прямоугольнику одновременно.

Формат входных данных
В первой строке задаются три целых числа: r, x0, y0
Во второй строке четыре целых числа: x1, y1, x2, y2

Ограничения:

• 1 <= radius <= 2000
• -104 <= xCenter, yCenter <= 104
• -104 <= x1 < x2 <= 104
• -104 <= y1 < y2 <= 104

Формат выходных данных
Выведите True, если круг и прямоугольник пересекаются, иначе - False.

«Кто ходит в гости по утрам, тот поступает мудро…»

Пятачок и Винни-Пух каждое утро ходят пить чай в гости к Кролику. Естественно, самым коротким путем.

К сожалению, однажды Винни-Пуху пришла в голову идея вырыть ловушку для Слонопотама. Самое обидное, что они с Пятачком ее даже вырыли. Поэтому теперь каждое утро, идя в гости к Кролику, они боятся в нее провалиться.

Напишите программу, которая посчитает длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика.

Ловушка для Слонопотама представляет собой яму абсолютно круглой формы. Путь является безопасным, если он не проходит по ловушке (но может проходить по ее границе).

Формат входных данных

Во входном файле записаны сначала координаты домика Винни-Пуха X_В Y_В, затем — координаты домика Кролика X_К Y_К, а затем — координаты центра и радиус ловушки X_Л Y_Л R_Л. Все координаты — целые числа из диапазона от –32000 до 32000. Радиус ловушки — натуральное число, не превышающее 32000.

Домики Винни-Пуха и Кролика не могут находиться внутри ловушки, но могут находиться на ее границе.

Формат выходных данных

Выведите в выходной файл одно число — длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика с тремя знаками после точки.

Заданы коэффициенты уравнения прямой ax + by + c = 0 и координаты точки A (xa, ya). Найдите точку B, которая является отражением точки A относительно заданной прямой.

Формат входных данных

В начале с клавиатуры вводятся коэффициенты уравнения прямой a, b, c, затем координаты точки A. Исходные данные являются целыми числами, по модулю не превышающими 1000

Формат выходных данных

Выведите координаты точки B с точностью до пятого знака после запятой.

В новом торговом центре проектируется вращающаяся дверь, которая на виде сверху представляет собой круг, разделенный на 4 равные части. Владельцы торгового центра знают, что самый большой товар, который у них будет продаваться, упаковывается в прямоугольные коробки шириной a,  длиной b и высотой c. При этом транспортировать такую коробку можно только поставив ее на одну из граней. Определите, какой минимальный радиус должен быть у вращающейся двери, чтобы покупатель мог унести такой товар (высота двери может быть сколь угодно большой). Считается, что покупатель при попытке унести коробку действует самым очевидным для себя способом - размещает коробку так, чтобы угол один из углов коробки оказался в углу между створками двери. Размерами покупателя можно пренебречь.

Формат входных данных
C клавиатуры вводятся натуральные числа a, b и c, не превосходящие 10000.

Формат выходных данных
Выведите минимально необходимый радиус двери с точностью не менее 5 знаков после запятой.

Винни Пух и Пятачок отправились воровать мед у пчел, и, в очередной раз влипли в неприятности. Пятачку опять потребовалось выстрелить из своего охотничьего ружья и пробить воздушный шарик, на котором Винни Пух поднялся к дуплу за медом. При этом желательно попасть именно в шарик, не задев медведя. Вычислите оптимальную позицию для стрельбы.

Поскольку Винни Пух очень любит покушать, то в данной задаче (да и не только в задаче) примем его за сферу радиуса  P. Центр медведя находится на высоте Hp над уровнем земли. Строго над медведем , находится еще одна сфера, радиуса S – воздушный шарик; центр шарика находится на высоте Hs над уровнем земли. Центры обеих сфер находятся на одной вертикальной прямой.  По понятным причинам гарантируется, что сферы не пересекаются J, однако могут касаться.

Считая, что ружье стреляет строго по прямой, вычислите минимальное расстояние L, на которое Пятачок должен отойти от места взлета, чтобы успешно поразить шарик. Шарик считается пораженным, если траектория пули хотя бы касается его поверхности; при этом если траектория пули касается медведя, то он считается невредимым.

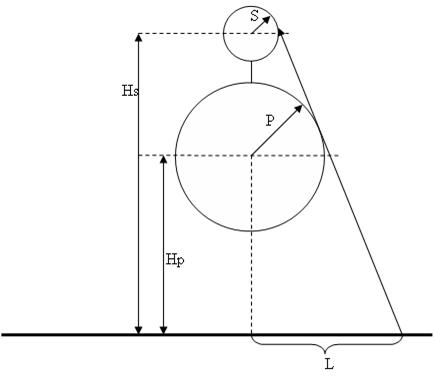
Формат входных данных

C клавиатуры вводятся положительные целые числа P, Hp, S и Hs, не превосходящие 10000.

Формат входных данных

Выведите минимальное расстояние от точки взлета, с которого можно поразить шарик из ружья с точностью не менее 5 знаков после запятой.

В рамках проекта по улучшению городской инфраструктуры вам необходимо провести анализ распределения зеленых насаждений (деревьев, кустарников и т.д.) вокруг новых жилых комплексов. Область вокруг жилых комплексов на плане города ограничена окружностью. Внутрь одной области, ограниченной окружностью, могут попадать несколько жилых комплексов. 

У вас есть массив points, где points[i] = [xi, yi] — координаты i-го зеленого насаждения на двумерной карте города.

Также у вас есть массив queries, где queries[j] = [xj, yj, rj] описывает j-ю круговую зоны, в которой необходимо оценить количество зеленых насаждений.

Для каждого запроса queries[j] вычислите количество зеленых насаждений, находящихся внутри j-й круговой зоны. Точки, находящиеся на границе зоны, также считаются входящими в эту зону.

Верните массив answer, где answer[j] — это количество зеленых насаждений в j-й круговой зоне.
 

В пространстве с прямоугольной системой координат находятся два куба. Про них известно следующее:

• сторона каждого куба равна 2, 
• центр (т.е. центр симметрии) каждого куба совпадает с началом данной системы координат,
• координаты вершин >первого куба A₁A₂A₃A₄A₅A₆A₇A₈ следующие: A₁(1, 1, 1), A₂(1, –1, 1), A₃(–1, –1, 1), A₄(–1, 1, 1), A₅(1, 1, –1), A₆(1, –1, –1), A₇(–1, –1, –1), A₈(–1, 1, –1), 
• вершины второго куба B₁B₂B₃B₄B₅B₆B₇B₈ пронумерованы так, что путем поворота кубы можно совместить, и при этом совместятся соответствующие их вершины (A₁ и B₁, A₂ и B₂, … , A₈ и B₈)
• координаты вершин второго куба даны во входном файле.

Требуется найти объем пересечения (т.е. общей части) этих кубов.

Входные данные
Во входных данных записаны 8 троек действительных чисел – координаты вершин второго куба B₁B₂B₃B₄B₅B₆B₇B₈.

Выходные данные
В выходной файл выведите одно число – искомый объем пересечения кубов. Ответ не должен отличаться от верного более чем на 0.00001.

Пользователь просматривает таблицу в Internet Explorer и пользуется для прокрутки изображения колесиком на мышке. При этом все изображение сдвигается вверх или вниз на T пикселов. Пользователю очень не нравится, когда курсор мыши оказывается на горизонтальных линиях, разделяющих строки таблицы. Поэтому он хочет выбрать такое положение для курсора мыши на экране, чтобы в процессе прокрутки до конца таблицы курсор как можно меньшее число раз пересекался с линиями таблицы.

При этом если в каком-то положении курсор оказывается на двух линиях таблицы, то это считается за два пересечения курсора с линиями таблицы. Если какую-то линию курсор мыши пересекает в двух положениях (то есть, например, высота курсора 10 пикселей, а при прокрутке таблица сдвигается на 7 пикселей, тогда курсор мыши может оказываться на одной линии в двух состояниях прокрутки), то это также считается за два пересечения.

Экран монитора имеет разрешение по вертикали U пикселей. Координаты введены так, что самые верхние точки экрана имеют координату 0, а нижние — координату U–1.

Курсор мыши имеет высоту H пикселов. Расположением курсора считается самая верхняя точка курсора. Таким образом, если мы говорим, что он расположен, например, в точке с координатами 0 на экране, то его изображение расположено в точках с координатами от 0 до H–1. Курсор мыши всегда целиком помещается на экране, то есть допустимыми координатами для его расположения являются координаты от 0 до U–H.>

Таблица, которую просматривает пользователь, имеет высоту L пикселов и состоит из N–1 строки, и, следовательно, в ней N горизонтальных линий, которые имеют координаты X₁, X₂, …, X_N. При этом 0=X₁<X₂<X₃<…<X_N=L–1.

В начальный момент времени таблица расположена так, что линия, имеющая координату 0 в таблице отображается в 0-й строке пикселов монитора. Далее при прокрутке таблица каждый раз сдвигается на T пикселов (то есть в 0-й строке монитора оказывается строка пикселов, имеющая в таблице координату T, координату 2T и т.д.). Так происходит до тех пор, пока на экране не окажется нижняя линия таблицы (которая имеет координату XN). После этого дальнейшая прокрутка не происходит (если изначально X_N<U, то прокрутка вообще не происходит).

Входные данные
Во входном файле задано сначала разрешение монитора по вертикали U, затем высота курсора мыши H, затем шаг прокрутки T. Далее задана высота таблицы L. Далее задано количество разделительных линий в таблице N, и координаты X₁, X₂,…,X_N, где расположены эти линии относительно начала таблицы.

Ограничения

• 10<U<512
• 1<H<U
• 1<T<U
• 2<N<200000
• 0=X₁<X₂<…<X_N=L–1≤10⁹.

Выходные данные
В выходной файл выведите сначала координату, в которой нужно расположить курсор мыши, а затем количество пересечений курсора мыши с линиями таблицы. В случае, если существует несколько начальных положений курсора мыши, выведите любое из них.

На плоскости задано N векторов – направленных отрезков, для каждого из которых известны координаты начала и конца (вектор, у которого начало и конец совпадают, называется нуль-вектором, можно считать, что нуль-вектор лежит на любой прямой, которая через него проходит). Введем следующие три операции над направленными отрезками на плоскости:

1) Направленные отрезки ненулевой длины, лежащие на пересекающихся прямых, можно заменить на их сумму, причем единственным образом. В этом случае отрезки переносятся вдоль своих прямых так, чтобы их начала совпадали с точкой пересечения прямых, и складываются по правилу сложения векторов (правилу параллелограмма, при этом началом результирующего вектора является точка пересечения прямых).

2) Направленные отрезки, лежащие на одной прямой, также можно заменить на их сумму. Для этого один из отрезков (любой) нужно перенести в начало второго из них и сложить по правилу сложения векторов на прямой:

Это правило применимо и в случае, когда один из векторов, или даже оба, являются нуль-векторами.

Заметим, что если складываемые векторы противоположно направлены и имеют одну и ту же длину, то результатом их сложения является нуль вектор.

3) В любой точке плоскости можно породить два противоположно направленных отрезка равной (в том числе и нулевой) длины:

Будем говорить, что две системы векторов эквивалентны, если от одной системы можно перейти к другой с помощью конечной последовательности перечисленных выше операций.

Требуется получить любую систему векторов, эквивалентную заданной, состоящую из как можно меньшего числа векторов.

Входные данные
В первой строке записано число N – количество заданных векторов (1 < N ≤ 1000). В каждой из следующих N строк через пробел записаны четыре числа, обозначающие координаты начала и конца каждого из векторов соответственно. Все координаты – целые числа, по модулю не превосходящие 1000.

Выходные данные
В первой строке следует записать число M – количество векторов в полученной системе (1 ≤ M ≤ N). В каждой из следующих M строк через пробел должны находиться четыре числа, обозначающие координаты начала и конца каждого из векторов соответственно. Все координаты – вещественные числа, записанные с 6 цифрами после точки.

В саду Бена расположено n ульев. Некоторые из них соединены друг с другом или с домом Бена прямыми дорожками. Бен гуляет только по дорожкам, переходя с одной на другую только возле очередного улья. Ни дом Бена, ни какой-либо улей не расположены на дорожке, соединяющей другие два улья. Дорожки организованы таким образом, что Бен может дойти от дома до любого улья только единственным способом.

Каждую неделю Бен делает обход ульев. Он начинает от своего дома и идет по дорожкам, посещая каждый улей по крайней мере один раз, минимизируя при этом общий путь. Сын Бена решил помочь своему стареющему отцу и проложить еще одну прямую дорожку между двумя ульями, так чтобы путь Бена от дома через все ульи с возвращением к дому стал как можно короче. Она, как и старые дорожки, проходить мимо дома или другого улья не должна.

Входные данные
На вход сначала подается число n — количество ульев (1≤n≤200).

Введем координаты так, что дом Бена будет располагаться в точке (0, 0). В следующих n строках входных данных записаны координаты ульев в саду Бена. Они не превосходят 10000 по абсолютному значению. Никакие два улья не совпадают, и нет ульев, расположенных в точке (0, 0). Будем считать, что они пронумерованы от 1 до n.
Следующие n строк описывают дорожки — каждая дорожка описывается номерами объектов, которые она соединяет. Дом Бена имеет номер 0.

Выходные данные
Выведите два числа — номера объектов, которые надо соединить дополнительной дорожкой. Если требуемой прямой дорожки, сокращающей общий путь Бена не существует, то выведите –1.

Дано N точек на плоскости, их надо покрасить в черный и белый цвета.

При этом должны присутствовать точки обоих цветов и должна существовать прямая, по одну сторону от которой все точки черные, по другую белые.

Требуется посчитать количество раскрасок, удовлетворяющих этим условиям.

Входные данные
В первой строке задано число 2≤N≤300. В следующих N строках заданы координаты точек.

Выходные данные
Выведите единственное число - количество различных раскрасок.

Джо - электрик-ковбой. Как у всех ковбоев у него есть лассо, как всем электрикам ему иногда приходиться залезать на столбы, и как все он ленив.

Вот и сейчас ему поручили проверить два стоящих на расстоянии d друг от друга столба высоты h₁ и h₂ соответственно. Чтобы убедиться, что все хорошо, Джо должен побывать на вершинах обоих столбов.

Электрик-ковбой посещает столбы следующим образом: сначала он выбирает один из столбов и просто взбирается на него. Выполнив все работы на вершине, он спускается по этому столбу на некоторую высоту (возможно до самой земли), достает свое лассо и цепляется им за некоторую точку второго столба (это может быть произвольная точка). После этого Джо прыгает и двигается вниз по дуге окружности с центром в точке, за которую зацепилось лассо, пока не достигнет либо другого столба, либо земли.

При этом если от начальной позиции электрика до конца его полета высота изменяется более чем на l, то ковбой набирает слишком большую скорость, больно ударяется и попадает в больницу, так и не выполнив работу. Поэтому Джо всегда аккуратно выбирает параметры прыжка.

Если в результате прыжка Джо оказался на земле, он подходит к другому столбу и взбирается на него. Если же Джо оказался на столбе, то он взбирается на вершину из той точки, в которой он оказался.



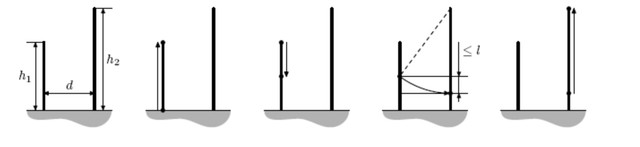
Джо просит вас помочь ему выполнить работу, сообщив какое минимальное расстояние ему придется лезть вверх по столбам.

Входные данные
Входной файл содержит четыре положительных целых числа: d, h₁, h₂ и l - расстояние между столбами, высоту первого и второго столбов и максимальный допустимый перепад высот при прыжке, соответственно. Все числа во входном файле не превышают 10⁶.

Выходные данные
Выведите ответ с максимальной возможной точностью. Ответ будет проверяться с точностью до 10⁻⁵.