| Условие задачи | | Прогресс | Попытки, все/успешные |
ID 55691.
Клад
Темы:
Динамическое программирование на графах
Комбинаторика
Однажды Юрик оказался в лесу у костра, где собрались \(n\) человек. Оказалось, что некоторые из них знакомы друг с другом. Для удобства пронумеруем людей целыми числами от \(1\) до \(n\). Обозначим как \(d_i\) количество людей, сидящих у костра, с которыми знаком \(i\)-й человек. Неожиданно оказалось, что два человека с номерами \(i\) и \(j\) (\(i \ne j\)) знакомы друг с другом тогда и только тогда, когда \(d_i = d_j\).
Вернувшись домой, Юрик задумался, какое минимальное количество пар людей могли быть знакомы, чтобы выполнялось это условие?
Формат входных данных
Единственная строка содержит одно целое число \(n\) (\(1 \le n \le 5\,000\)) — количество людей.
Формат выходных данных
Выведите одно целое число — минимальное количество пар знакомых людей.
Рассмотрим первый пример из условия. Возможны следующие варианты:
-
Любые два человека знакомы друг с другом. В этом случае количество пар знакомых людей равно \(\frac{4 \cdot 3}{2} = 6\).
-
Некоторые три человека попарно знакомы друг с другом, четвертый человек не знаком ни с кем. В этом случае количество пар знакомых людей равно \(3\).
| |
![]()
|
1/
1
|
|
Темы:
Динамическое программирование на графах
Приехав в Хоббитанию, белый маг Гэндальф принялся рассказывать Бильбо последние новости из Средиземья. Больше всего впечатлительного хоббита поразил рассказ о Большом огромном коллайдере - только представить себе гигантских размеров кольцо, зарытое под землей!
Вдохновленный рассказом мага, Бильбо решил смастерить собственный коллайдер прямо у себя в норе. До начала строительства нора представляет собой множество комнат, причем некоторые пары комнат соединены коридорами. Как это принято у хоббитов, из любой комнаты в любую другую можно добраться по коридорам ровно одним способом.
Бильбо хочет прокопать новые коридоры в норе, но так как копать будут только Фродо и сам Бильбо (не Гэндальф же!) , есть возможность прокопать только один или два новых коридора.
После этого последовательность из нескольких комнат будет названа коллайдером. При этом должны быть выполнены следующие условия: первая комната в этой последовательности соединена коридором со второй, вторая - с третьей, и так далее, наконец, последняя комната последовательности должна быть соединена с первой. Кроме того, каждая комната может входить в эту последовательность не более одного раза.
Помогите Бильбо выбрать такие один или два новых коридора, чтобы коллайдер имел максимальную возможную длину, то есть состоял из максимального возможного числа комнат.
Входные данные
В первой строке входного файла содержится целое число n (3≤n≤100000) - число комнат в норе Бильбо.
В следующих n−1 строках содержатся по два целых числа - номера комнат, соединенных коридорами. Комнаты нумеруются от 1 до n.
Выходные данные
В первую строку выходного файла выведите максимально возможное число комнат в коллайдере.
На следующих одной или двух строках выведите пары номеров комнат, между которыми следует прокопать новые коридоры.
Если существует несколько возможных планов строительства коллайдера максимальной длины, выведите любой из них.
Примечание
В первом примере коллайдер состоит из комнат с номерами 1, 2, 3 и 4 (именно в этом порядке), во втором примере - 1, 3, 2, 4.
| |
![]()
|
1/
0
|
ID 54942.
Реки
Темы:
Динамическое программирование на графах
Почти все Королевство Байтленд покрыто лесами и реками. Малые реки сливаются в более крупные реки, которые, в свою очередь, сливаются друг с другом; в конечном счете, все реки сливаются вместе в одну большую реку. Большая река впадает в море вблизи города Байттаун.
В Байтленде имеется n лесозаготовительных поселков, каждый из которых расположен вблизи какой-либо реки. В настоящее время в Байттауне находится большая пилорама, которая обрабатывает все деревья, срубленные в Королевстве. Деревья сплавляются вниз по рекам от поселков, где они срублены, к пилораме в Байттауне. Король Байтленда решил поставить k дополнительных пилорам в поселках, чтобы уменьшить стоимость сплава деревьев. После установки пилорам деревья не обязательно должны сплавляться в Байттаун, а могут быть обработаны на ближайшей пилораме, находящейся ниже по течению рек. Очевидно, что деревья, срубленные в окрестности поселка с пилорамой, вообще не сплавляются по рекам.
Необходимо отметить, что реки в Байтленде не разветвляются. Из этого следует, что для каждого поселка существует единственный путь сплава деревьев вниз по течению рек от него в Байттаун.
Королевские счетоводы подсчитали количество деревьев, срубаемых в каждом поселке за год. Вам необходимо определить, в каких поселках следует установить пилорамы, чтобы минимизировать общую стоимость сплава деревьев за год. Стоимость сплава одного дерева составляет один цент за каждый километр пути.
Задание
Напишите программу, которая:
<> * читает из стандартного ввода количество поселков, количество дополнительных пилорам, которые будут установлены, количество срубленных в каждом поселке деревьев и описание рек,
*вычисляет минимальную стоимость сплава деревьев после установки дополнительных пилорам,
*выводит результат в стандартный вывод.
Входные данные
Первая строка входных данных содержит два целых числа: n — количество поселков, не считая Байттауна (2 ≤ n ≤ 100), и k
— количество дополнительных пилорам, которые будут установлены (1 ≤ k ≤ 50 и k ≤ n). Поселки нумеруются числами 1 , 2 ,...., n , а Байттаун имеет номер 0.
Каждая из последующих n строк содержит три целых числа, разделенных одним пробелом. Строка i + 1 содержит:
wi — количество деревьев, срубаемых в поселке i за год (0 ≤ wi ≤ 10 000),
vi — ближайший поселок (либо Байттаун) вниз по реке от поселка i (0 ≤ vi ≤ n),
di — расстояние (в километрах) по реке от поселка i до поселка vi (1 ≤ di ≤ 10 000).
Гарантируется, что суммарная стоимость сплава всех деревьев к пилораме в Байттауне не превосходит 2 000 000 000 центов в год.
В 50% тестов число n не превосходит 20.
Выходные данные
Первая и единственная строка выходных данных должна содержать одно целое число: минимальную стоимость сплава (в центах).
Пояснения
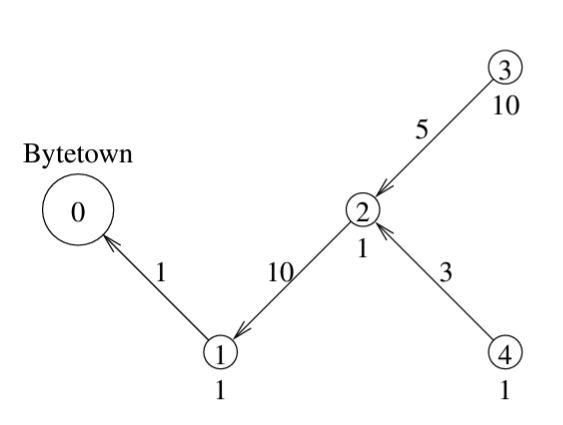
Рисунок сверху иллюстрирует входные данные примера. Номера поселков указаны внутри кругов. Числа под кругами обозначают количество деревьев, срубаемых вблизи данного поселка. Числа над стрелками указывают длины рек.
Пилорамы должны быть установлены в поселках 2 и 3.
| |
![]()
|
1/
1
|
|
Темы:
Динамическое программирование на графах
Эвристические методы
Сверхсекретный завод, расположенный высоко в горах, занимается изготовлением новейших систем контроля торсионных полей – нанокристаллов. Нанокристалл состоит из нескольких атомов, некоторые из которых попарно связаны сверхпрочными торсионными связями.
Нанокристалл стабилен, если между любыми двумя его атомами можно построить соединяющую их цепочку связей, возможно с использованием других атомов. Например, из четырех атомов A, B, C и D, в котором между собой связаны пары A - B, A - C, B - C и B - D, стабилен. Если же, например, в нанокристалле из данных четырех атомов связаны только пары A - B и C - D, то кристалл нестабилен, поскольку, например, A и C не соединены никакой цепочкой связей.
Для любой пары атомов стабильного нанокристалла определена их взаимная удаленность – минимальная длина цепочки из связей, которая их соединяет. Например, рассмотрим описанный выше нанокристалл. Взаимная удаленность атомов A и B равна единице (они соединены напрямую), а взаимная удаленность C и D равна двум (они соединены цепочками C - B - D и C - A - B - D, длина кратчайшей цепочки равна двум).
Важнейшей характерикой стабильного нанокристалла является его емкость. Емкость нанокристалла равна сумме взаимных удаленностей всех пар его атомов. Например, емкость нанокристалла равна 8.
Недавно на завод поступил заказ – разработать стабильный нанокристалл заданной емкости c. При этом как число атомов в нанокристалле, так и число связей может быть произвольным. Помогите ученым разработать такой кристалл!
Входные данные
На вход программы поступает число c (1<c<10 000).
Выходные данные
В первой строке выведите два целых числа n и m – количество атомов и связей в разработанном нанокристалле, соответственно. Будем считать, что атомы нанокристалла пронумерованы от 1 до n. Следующие m строк должны содержать по два целых числа – пары атомов, которые следует соединить торсионными связями. Если решений несколько, выведите любое.
Если искомого нанокристалла не существует, выведите в первой и единственной строке выходных данных два нуля.
| |
![]()
|
2/
2
|
|
Темы:
"Длинная" арифметика
Динамическое программирование на графах
Широкое распространение в стандартных библиотеках многих языков программирования получила реализация сбалансированных деревьев на основе так называемых красно-черных деревьев. В данной задаче вам предлагается посчитать количество красно-черных деревьев заданной формы.
Напомним, что двоичным деревом называется набор вершин, организованных в виде дерева. Каждая вершина имеет не более двух детей, один из которых называется левым, а другой — правым. Как левый, так и правый ребенок, а также оба могут отсутствовать.
Если вершина \(Y\) — ребенок вершины \(X\), то говорят, что вершина \(X\) является родителем вершины \(Y\). У каждой вершины дерева, кроме одной, есть ровно один родитель. Единственная вершина, не имеющая родителя, называется корнем дерева.
Соединим каждую вершину кроме корня с ее родителем. Заметим, что для каждой вершины существует ровно один путь, ведущий в нее от корня.
Двоичное дерево называется красно-черным, если каждая его вершина раскрашена в красный либо в черный цвет, причем выполняются следующие условия:
-
если вершина красная, то ее родитель — черный;
-
количество черных вершин на пути от корня до любой вершины, у которой отсутствует хотя бы один ребенок, одно и то же.
Примеры двоичного дерева, вершины которого раскрашены в два цвета, приведены на следующем рисунке.
Если считать закрашенные вершины черными, а незакрашенные — красными, то дерево на рисунке (а) является красно-черным деревом, а деревья на рисунках (б) и (в) — нет. Для дерева на рисунке (б) нарушается первое свойство — у красной вершины 5 родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство — на пути от корня до вершины 1 одна черная вершина, а, например, на пути от корня до вершины 3 — две.
Для заданного двоичного дерева подсчитайте число способов раскрасить его вершины в черный и красный цвет так, чтобы оно стало красно-черным деревом.
Формат входных данных
Первая строка содержит число \(n\) — количество вершин в дереве (\(1 \le n \le 1000\)).
Пусть вершины дерева пронумерованы числами от \(1\) до \(n\). Следующие \(n\) строк содержат по два числа — для каждой вершины заданы номера ее левого и правого ребенка. Если один из детей отсутствует, то вместо его номера записан ноль. Гарантируется, что входные данные корректны, то есть набор чисел действительно задает двоичное дерево.
Формат выходных данных
Выведите одно число — количество способов раскрасить вершины заданного во входном файле двоичного дерева в красный и черный цвета так, чтобы оно стало красно-черным деревом.
Все допустимые способы раскрасить вершины дерева из первого примера приведены на следующем рисунке.
| |
![]()
|
1/
1
|
|
Темы:
Динамическое программирование на графах
Сегодня Игорь получил долгожданное разрешение на проведение эксперимента по изучению протекания химических реакций в магнитном поле. При этом используются две установки — генератор магнитного поля и манипулятор, соединяющий реагенты.
Эксперимент разбит на некоторое количество этапов, при этом некоторые из них могут быть выполнены только после завершения определенного набора других этапов. Правда известно, что хотя бы один способ проведения эксперимента существует. На каждом этапе Игорь должен управлять ровно одной из двух установок — либо генератором, либо манипулятором.
Игорь очень дорожит своим временем, и поэтому он хочет провести эксперимент, совершив наименьшее количество перемещений между пультами управления установками. Помогите ему узнать, в каком порядке следует выполнять этапы, чтобы этого добиться.
Формат входных данных
На первой строке записано целое число \(n\) — количество этапов эксперимента (\(1 \le n \le 100\)).
Следующие \(n\) строк содержат описание этапов. Пронумеруем этапы от 1 до \(n\) в некотором произвольном порядке. Тогда \(i\)-я из этих строк описывает \(i\)-й этап. Каждый этап описывается последовательностью целых чисел. Первое число равно нулю, если на этом этапе Игорь управляет генератором, и единице, если он управляет манипулятором. Затем записано целое число \(r_i\) — количество этапов, которые должны быть выполнены перед выполнением данного. За ним следуют номера этих этапов — \(r_i\) различных целых чисел в диапазоне от 1 до \(i - 1\).
Формат выходных данных
На первой строке выведите минимальное количество перемещений, которые придется совершить Игорю. На второй строке выведите перестановку чисел от 1 до \(n\) — последовательность, в которой следует выполнять этапы. Если решений несколько, выведите любое.
| |
![]()
|
2/
1
|
|
Темы:
Динамическое программирование на графах
Бор
На одном из телеканалов каждую неделю проводится следующая лотерея. В течение недели участники делают свои ставки. Каждая ставка заключается в назывании какого-либо M-значного числа в системе счисления с основанием K (то есть, по сути, каждый участник называет M цифр, каждая из которых лежит в диапазоне от 0 до K−1). Ведущие нули в числах допускаются.
В некоторый момент прием ставок на текущий розыгрыш завершается, и после этого ведущий в телеэфире называет выигравшее число (это также M-значное число в K-ичной системе счисления). После этого те телезрители, у кого первая цифра их числа совпала с первой цифрой числа, названного ведущим, получают выигрыш в размере A1 рублей. Те, у кого совпали первые две цифры числа — получают A2 рублей (при этом если у игрока совпала вторая цифра, но не совпала первая, он не получает ничего). Аналогично угадавшие первые три цифры получают A3 рублей. И так далее. Угадавшие все число полностью получают Am рублей. При этом если игрок угадал t первых цифр, то он получает At рублей, но не получает призы за угадывание t−1, t−2 и т.д. цифр. Если игрок не угадал первую цифру, он не получает ничего.
Напишите программу, которая по известным ставкам, сделанным телезрителями, находит число, которое должна назвать телеведущая, чтобы фирма-организатор розыгрыша выплатила в качестве выигрышей минимальную сумму. Для вашего удобства ставки, сделанные игроками, уже упорядочены по неубыванию.
Входные данные
В первой строке задаются числа N (количество телезрителей, сделавших свои ставки, 1 ≤ N ≤ 100000), M (длина чисел 1 ≤ M ≤ 10) K (основание системы счисления 2 ≤ K ≤ 10). В следующей строке записаны M чисел A1, A2, ..., AM, задающих выигрыши в случае совпадения только первой, первых двух,... , всех цифр (1 ≤ A1 ≤ A2 ≤ ... ≤ AM ≤ 100000). В каждой из следующих N строк записано по одному M-значному K-ичному числу. Числа идут в порядке неубывания.
Выходные данные
В первой строке выведите искомое число (если решений несколько — выведите любое из них), а во второй строке — сумму, которую при назывании телеведущей первого числа придется выплатить в качестве выигрыша.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10 3 2
1 3 100
000
000
001
010
100
100
100
100
110
111 |
011
6 |
| 2 |
1 1 10
100
0 |
1
0 |
| |
![]()
|
4/
2
|
|
Темы:
Динамическое программирование на графах
Эн идет в свой Грибной лес собирать грибы.
В Грибном лесу m ориентированных дорожек, соединяющих n деревьев. На каждой дорожке растут грибы. Когда Эн проходит по дорожке, он собирает все грибы на этой дорожке. Однако, в Грибном лесу такая плодородная почва, что грибы растут с фантастической скоростью. Новые грибы вырастают, как только Эн заканчивает собирать грибы на дорожке. А именно, после того, как Эн проходит по дорожке в i-й раз, вырастает на i грибов меньше, чем было до этого прохода. Таким образом, если на дорожке изначально было x грибов, то Эн соберет x грибов в первый проход, x - 1 гриб во второй, x - 1 - 2 гриба в третий и так далее. Однако, количество грибов не может стать меньше 0.
Например, пусть изначально на дорожке росло 9 грибов. Тогда количество грибов, которое соберет Эн, равно 9, 8, 6 и 3 для проходов с первого по четвертый. Начиная с пятого прохода и далее Эн ничего не сможет собрать с этой дорожки (но все еще может по ней ходить).
Эн решил начать от дерева s. Какое максимальное количество грибов он может собрать, передвигаясь только по описанным дорожкам?
Входные данные:
Первая строка содержит два целых числа n и m (1 ≤ n ≤ 300000, 0 ≤ m ≤ 300000) — количество деревьев и количество ориентированных дорожек в Грибном лесу, соответственно.
Каждая из следующих m строк содержит три целых числа x, y и w (1 ≤ x, y ≤ n, 0 ≤ w ≤ 108), описывающих дорожку, которая ведет от дерева x к дереву y с w грибами изначально. Возможны дорожки, которые ведут от дерева к нему же, а также несколько дорожек, соединяющих одну и ту же пару деревьев.
Последняя строка содержит одно целое число s (1 ≤ s ≤ n) — начальную позицию Эна.
Выходные данные:
Выведите одно целое число — максимальное число грибов, которое может собрать Эн на своем пути.
Примеры:
| Входные данные |
Выходные данные |
2 2
1 2 4
2 1 4
1 |
16 |
3 3
1 2 4
2 3 3
1 3 8
1 |
8 |
Пояснения:
В первом примере Эн может три раза пройти по кругу и собрать 4 + 4 + 3 + 3 + 1 + 1 = 16 грибов. После этого не будет грибов, которые Эн может собрать.
Во втором примере Эн может пойти к дереву 3 и собрать 8 грибов на дорожке от дерева 1 до дерева 3.
| |
![]()
|
202/
15
|
|
Темы:
Динамическое программирование на графах
Дан граф из n вершин и m ориентированных ребер. В каждой вершине записана некоторая строчная латинская буква.
Определим величину пути как наибольшее количество раз, которое какая-то буква встречалась на этом пути. Например, если буквы на пути образуют строку «abaca», то величина этого пути равна 3.
Ваша задача — найти путь с наибольшей величиной.
Входные данные:
Первая строка содержит два целых числа n, m (1 ≤ n, m ≤ 200000), означающих, что в графе n вершин и m ориентированных ребер.
Вторая строка содержит строку s, состоящую только из строчных латинских букв. Символ номер i — это буква, записанная в вершине номер i.
Далее следуют m строк. Каждая из этих строк содержит два целых числа x, y (1 ≤ x, y ≤ n), описывающих ориентированное ребро из x в y. Обратите внимание, x может быть равно y, и могут быть несколько ребер между x и y.
Кроме того, граф может быть несвязным.
Выходные данные:
Выведите одно число — максимальную величину пути. Если существуют пути со сколь угодно большой величиной, выведите -1.
Примеры:
| Входные данные |
Выходные данные |
5 4
abaca
1 2
1 3
3 4
4 5 |
3 |
6 6
xzyabc
1 2
3 1
2 3
5 4
4 3
6 4 |
-1 |
10 14
xzyzyzyzqx
1 2
2 4
3 5
4 5
2 6
6 8
6 5
2 10
3 9
10 9
4 6
1 10
2 8
3 7 |
4 |
| |
![]()
|
108/
55
|
|
Темы:
Динамическое программирование на графах
Дан ориентированный взвешенный ациклический граф. Требуется найти в нем кратчайший путь
из вершины s в вершину t.
Входные данные:
Первая строка входного файла содержит четыре целых числа n, m, s и t - количество вершин, ребер графа, начальная и конечная вершина соответственно (1 <= n <= 100000; 0 <= m <= 200000; 1 <= s, t <= n).
Следующие m строк содержат описания ребер по одной на строке.
Ребро номер i описывается тремя целыми числами bi, ei и wi - началом, концом и длиной ребра соответственно (1 <= bi, ei <= n; |wi| <= 1000).
Граф не содержит циклов и петель.
Выходные данные:
Первая строка выходного файла должна содержать одно целое число - длину кратчайшего пути из s в t.
Если пути из s в t не существует, выведите "Unreachable".
Примеры:
| Входные данные |
Выходные данные |
2 1 1 2
1 2 -10 |
-10 |
2 1 2 1
1 2 -10 |
Unreachable |
| |
![]()
|
416/
96
|
|
Темы:
Динамическое программирование
Динамическое программирование на графах
Алгоритмы на графах
Обход в глубину
В тридесятом государстве есть N деревень. Некоторые пары деревень соединены дорогами. В целях экономии, “лишних” дорог нет, т.е. из любой деревни в любую можно добраться по дорогам единственным образом.
Новейшие исследования показали, что тридесятое государство находится в сейсмически опасной зоне. Поэтому глава государства захотел узнать, какой именно ущерб может принести его державе землетрясение. А именно, он хочет узнать, какое минимальное число дорог должно быть разрушено, чтобы образовалась изолированная от остальных группа ровно из P деревень такая, что из любой деревни из этой группы до любой другой деревни из этой группы по-прежнему можно будет добраться по неразрушенным дорогам (группа изолирована от остальных, если никакая неразрушенная дорога не соединяет деревню из этой группы с деревней не из этой группы).
Вы должны написать программу, помогающую ему в этом.
Формат входных данных
Первая строка входного файла содержит два числа: N и P (1 ≤ P ≤ N ≤ 150). Все остальные строки содержат описания дорог, по одному на строке: описание дороги состоит из двух номеров деревень (от 1 до N), которые эта дорога соединяет. Все числа во входном файле разделены пробелами и/или переводами строки.
Формат выходных данных
В выходной файл выведите единственное число — искомое количество дорог.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3 2
1 2
3 2 |
1 |
|
| 2 |
11 6
1 2
1 3
1 4
1 5
2 6
2 7
2 8
4 9
4 10
4 11 |
2 |
группа деревень (1, 2, 3, 6, 7, 8) окажется изолированной от остальных, если разрушить дороги 1–4 и 1–5. |
| |
![]()
|
11/
1
|
|
Темы:
Динамическое программирование на графах
Обход в глубину
Система непересекающихся множеств
Гурман Яблочков работает редактором известного гастрономического издания. Он разъезжает по всему миру, дегустируя новые изыски именитых шеф-поваров самых фешенебельных ресторанов высокой кухни. У Яблочкова есть свой фирменный способ ревью: в каждом заведении Яблочков заказывает два набора блюд в разные дни. Все заказанные блюда разные, так как Яблочков не любит есть одно и то же. Для каждой пары блюд из разных наборов он точно помнит, какое из них лучше по его ощущениям, или что они одинаковы по вкусовым качествам. Затем гурман оценивает каждое блюдо положительным целым числом.
Однажды, во время очередной ревизии, ресторан кельтской средневековой кухни «Пуассон», подающий суп из каштанов с пихтой, теплый содовый хлеб, пряный лимонный пирог и другую народную еду, очень приятно удивил гурмана своим разнообразным меню, и эксперт заказал слишком много. Поэтому ему нужна помощь в оценке блюд.
Гурман в первый день дегустировал набор из n блюд, во второй день набор из m блюд. Он составил таблицу ощущений a размером nm, в которой описал свои впечатления. Если по мнению эксперта блюдо i из первого набора лучше блюда j из второго набора, то aij равно « > », в противоположном случае aij равно « < ». Блюда также могут быть равны по уровню, тогда aij равно « = ».
Теперь Яблочков хочет, чтобы вы помогли ему оценить каждое блюдо в наборах целым положительным числом. Так как Яблочков очень строгий дегустатор, то постарается оценить блюда так, чтобы максимальная из оценок была как можно меньше. В то же время Яблочков очень справедливый, поэтому никогда не оценивает блюда так, чтобы это шло вразрез с его ощущениями. Другими словами, если aij равно « < », то оценка блюда i из первого набора должна быть меньше оценки блюда j из второго набора, если aij равно « > », то должна быть больше, а если aij равно « = », то должна совпадать.
Помогите Яблочкову выставить оценки каждому блюду из обоих наборов так, чтобы это согласовывалось с его ощущениями, или определите, что это невозможно.
Входные данные
В первой строке заданы два целых числа n и m (1 ≤ n, m ≤ 1000 ) — количества блюд в каждый из двух дней.
Каждая из следующих n строк содержит строку из m символов. j-й символ в i-й строке задаёт значение aij. Все строки состоят только из символов « < », « > » и « = ».
Выходные данные
В первой строке выведите « Yes » (без кавычек), если можно сделать корректную оценку всем блюдам и « No » (без кавычек), если иначе.
В случае, если сделать корректную оценку можно, во второй строке выведите n целых чисел — оценки блюд первого набора, а в третьей строке m целых чисел — оценки блюд второго набора.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3 4
>>>>
>>>>
>>>> |
Yes
2 2 2
1 1 1 1 |
Все блюда первого дня лучше всех блюд второго дня. Значит, самой высокой оценкой будет 2 для всех блюд первого дня. |
| 2 |
3 3
>>>
<<<
>>> |
Yes
3 1 3
2 2 2 |
|
| 3 |
3 2
==
=<
== |
No |
Таблица противоречива: нет ни одного набора оценок, который удовлетворял бы ей. |
| |
![]()
|
11/
4
|
|
Темы:
Динамическое программирование на графах
Древовидные структуры данных
Рассмотрим сеть из N (2≤N≤100) вершин, помеченных 1…N. Каждая вершина обозначена как посылатель, получатель или ни то, ни другое. Количество посылателей S равно количеству получателей (S≥1).
Связи между двумя вершинами в сети могут быть описаны как список направленных ребер каждое в виде i→j, обозначающее, что вершина i может передать информацию вершине j. Интересно, что все эти рёбра удовлетворяют свойству i<j, кроме K которые удовлетворяют свойству i>j (0≤K≤2). Нет циклов (ребер вида i→i).
Описание схемы маршрутизации состоит из множества S направленных путей от посылателей к получателям таких, что никакие два из этих путей не имею общую конечную точку. То есть пути соединяют различных посылателей с различными получателями. Путь от посылателя s к получателю r может быть описан как последовательность вершин
s=v0→v1→v2→?→ve=r
такая что направленные ребра vi→vi+1 существуют для всех 0≤i<e. Одна вершина может появиться более чем один раз в одном и том же пути.
Посчитайте количество различных схем маршрутизации, таких, что каждое направленное ребро проходится ровно один раз. Поскольку ответ может быть очень большим, выводите его по модулю 109+7. Гарантируется, что существует хотя бы одна схема маршрутизации, удовлетворяющая ограничениям.
Каждый ввод содержит T (1≤T≤20) тестов, которые требуется решать независимо. Гарантируется, что сумма N2 всех тестов не превысит 2⋅104.
Входные данные:
Первая строка содержит T, количество тестов.
Первая строка каждого теста содержит целые числа N и K. Заметим, что S не определяется явно во вводе.
Вторая строка каждого теста содержит строку длины N. i-ый символ строки равен S если i-ая вершина посылатель, R - если i-ая вершина - получатель, . - если i-ая вершина - ни то, ни другое. Количества символов R и S равны. Есть хотя бы один символ S.
Каждая из N последующих строк теста содержит битовую строку из N нулей и единиц. j-ый бит в i-ой строке равен 1, если существует направленное ребро от вершины i к вершине j, и 0 в протвном случае. Поскольку петель нет, на главной диагонали все нули. Более того имеется ровно K единиц ниже главной диагонали.
Последовательные тесты разделены пустыми строками для читабельности.
Выходные данные:
Для каждого теста выведите количество схем маршрутизации таких, что каждое ребро проходится ровно один раз, по модулю 109+7. Гарантируется, что существует хотя бы одна валидная схема маршрутизации.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
2
8 0
SS....RR
00100000
00100000
00011000
00000100
00000100
00000011
00000000
00000000
13 0
SSS.RRRSS.RR.
0001000000000
0001000000000
0001000000000
0000111000000
0000000000000
0000000000000
0000000000000
0000000001000
0000000001000
0000000000110
0000000000000
0000000000000
0000000000000 |
4
12 |
Для первого теста ребра таковы 1→3,2→3,3→4,3→5,4→6,5→6,6→7,6→8.
Имеется четыре схемы маршрутизации:
1→3→4→6→7,2→3→5→6→8
1→3→5→6→7,2→3→4→6→8
1→3→4→6→8,2→3→5→6→7
1→3→5→6→8,2→3→4→6→7
Для второго теста 1→4,2→4,3→4,4→5,4→6,4→7,8→10,9→10,10→11,10→12.
Одна из возможных схем маршрутизации:
1→4→5
2→4→7
3→4→6
8→10→12
9→10→11
В общем случае посылатели {1,2,3} могут маршрутизироваться некоторой перестановкой получателей {5,6,7}, и посылатели {8,9} могут маршрутизироваться некоторой перестановкой получателей {11,12} давая ответ 6 ⋅ 2=12.
|
| 2 |
2
5 1
SS.RR
00101
00100
10010
00000
00000
6 2
S....R
001000
000100
010001
000010
001000
000000 |
3
1 |
Для первого теста, ребра 1→3,1→5,2→3,3→1,3→4.
имеется три схемы маршрутизации:
1→3→1→5, 2→3→4
1→3→4, 2→3→1→5
1→5, 2→3→1→3→4
Для второго теста 1→3,2→4,3→2,3→6,4→5,5→3.
Имеется только одна схема мартшрутизации: 1→3→2→4→5→3→6. |
| 3 |
5
3 2
RS.
010
101
100
4 2
.R.S
0100
0010
1000
0100
4 2
.SR.
0000
0011
0100
0010
5 2
.SSRR
01000
10101
01010
00000
00000
6 2
SS..RR
001010
000010
000010
000010
100101
000000 |
2
1
2
6
24 |
|
| |
![]()
|
1/
1
|