Рассмотрим таблицу, состоящую из N строк и M столбцов. Если в каждой ячейке такой таблицы стоит целое число, назовем такую таблицу целочисленной матрицей. Скажем, что эта матрица кратна чиcлу p, если все числа в ее ячейках кратны p.
Рассмотрим теперь суммы элементов матрицы по строкам и столбцам соответственно. Обозначим сумму чисел i-й строки за Hi, а сумму чисел j-го столбца за Vj. Упорядоченный набор чисел (H
1, H
2, …, H
N, V
1, V
2, …, V
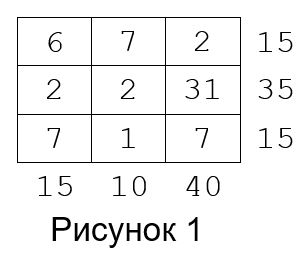
M) назовем профилем матрицы. Скажем, что матрица почти кратна p, если все числа, входящие в ее профиль, кратны p. Почти кратная 5 матрица и ее профиль изображены на рисунке 1.
Если две матрицы A и B имеют одинаковый размер, причем элемент, стоящий на пересечении i-й строки и j
-го столбца в матрице A отличается от соответствующего элемента матрицы B не более чем на p, скажем, что A отличается от B не более чем на p. Скажем, что матрица B похожа на матрицу A относительно числа p, если
1. отличается от не более чем на p
2. профили B и A совпадают.
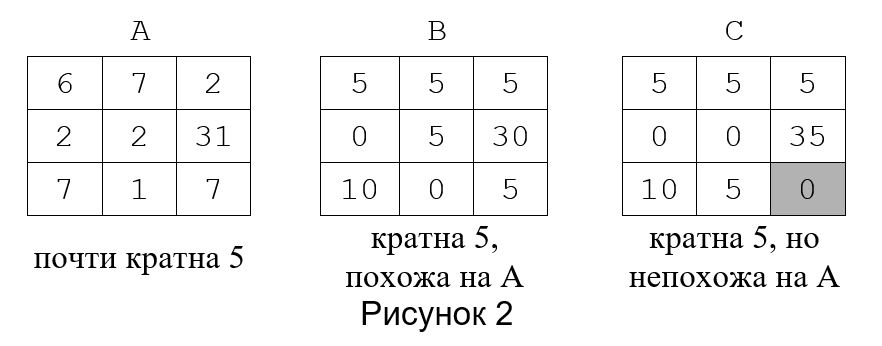
На рисунке 2 изображены две похожие относительно числа 5 матрицы, первая из них почти кратна 5, а вторая кратна 5. Третья матрица на рисунке 2 тоже кратна 5, но непохожа на первую (хотя похожа на вторую).
Дано число p и почти кратная p матрица A. Ваша задача - найти такую матрицу B, чтобы она была кратна p и похожа на A относительно p.
Входные данные
В первой строке входных данных задаются целые числа p (1 <= p <= 10), N и M (1 <= N, M <= 30). Следующие N строк содержат по M целых неотрицательных чисел, не превышающих 1000, которые являются элементами исходной матрицы A.
Выходные данные
Выведите матрицу B по строкам - сначала M элементов первой строки, затем M элементов второй, и т. д. Разделяйте числа пробелами и/или переводами строк. Заботиться о красивом форматировании таблицы не надо. Если искомой матрицы не существует, выведите единственное число - "-1". Если решений несколько, выведите любое из них.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 3 3
1 2 3
2 3 1
3 1 2
|
3 0 3
0 3 3
3 3 0
|