Задача: В школу на велосипеде

Петя любит ездить в школу на велосипеде. Но ездить на велосипеде по тротуарам запрещено, а ездить по дороге опасно. Поэтому Петя ездит только по специальным велосипедным дорожкам. К счастью, и Петин дом, и Петина школа находятся в непосредственной близости от таких дорожек.

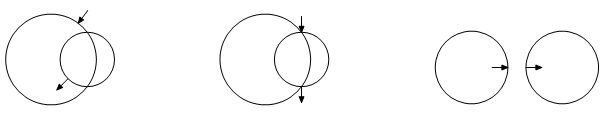
В городе, где живет Петя, есть ровно две велосипедных дорожки. Каждая дорожка имеет форму окружности. В точках их пересечения можно переехать с одной дорожки на другую.

Петя знает точку, в которой он заезжает на дорожку, и точку, в которой следует съехать, чтобы попасть в школу. Петю заинтересовал вопрос: какое минимальное расстояние ему следует проехать по дорожкам, чтобы попасть из дома в школу.

Входные данные
Будем считать, что в городе введена прямоугольная декартова система координат.

Первые две строки входных данных описывают велосипедные дорожки. Каждая из них содержит по три целых числа – координаты центра окружности, которую представляет собой соответствующая дорожка, и ее радиус. Координаты и радиус не превышают 200 по абсолютной величине, радиус – положительное число. Гарантируется, что дорожки не совпадают.

Следующие две строки содержат по два вещественных числа – координаты точки, где Петя заезжает на дорожку, и точки, в которой Петя съезжает с дорожки. Гарантируется, что каждая из точек с высокой точностью лежит на одной из дорожек (расстояние от точки до центра одной из окружностей отличается от ее радиуса не более, чем на 10^-8). Точки могут лежать как на одной дорожке, так и на разных.

Выходные данные
Выведите  минимальное расстояние, которое следует проехать Пете по велосипедным дорожкам, чтобы попасть из дома в школу. Ответ должен отличаться от правильного не более, чем на 10^-4.

Если доехать из дома до школы по велосипедным дорожкам невозможно, выведите  число -1.

Ваш ответ: