| | | |
|
Дейкстра: восстановление пути
Алгоритм Дейкстры
Дан ориентированный взвешенный граф. Найдите кратчайший путь от одной заданной вершины до другой.
Формат входных данных
В первой строке содержатся три числа: N, S и F (1≤N≤100, 1≤S, F≤N), где N – количество вершин графа, S – начальная вершина, а F – конечная. В следующих N строках вводится по N чисел, не превосходящих 100, – матрица смежности графа, где -1 означает отсутствие ребра между вершинами, а любое неотрицательное число – присутствие ребра данного веса. На главной диагонали матрицы записаны нули.
Формат выходных данных
Требуется вывести последовательно все вершины одного (любого) из кратчайших путей, или одно число -1, если пути между указанными вершинами не существует.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 2 1
0 1 1
4 0 1
2 1 0 |
2 3 1
|
| |
![]()
|
|
Заправки-2
Алгоритм Дейкстры
В стране N городов, некоторые из которых соединены между собой дорогами. Для того, чтобы проехать по одной дороге, требуется один бак бензина. Помимо этого у вас есть канистра для бензина, куда входит столько же топлива, сколько входит в бензобак.
В каждом городе бак бензина имеет разную стоимость. Вам требуется добраться из первого города в N-й, потратив как можно меньшее денег.
В каждом городе можно заправить бак, заправить бак и канистру или же перелить бензин из канистры в бак. Это позволяет экономить деньги, покупая бензин в тех городах, где он стоит дешевле, но канистры хватает только на одну заправку бака!
Формат входных данных
В первой строке вводится число N (1<=N<=100), в следующей строке идет N чисел, i-е из которых задает стоимость бензина в i-м городе (всё это целые числа из диапазона от 0 до 100). Затем идет число M – количество дорог в стране, далее идет описание самих дорог. Каждая дорога задается двумя числами – номерами городов, которые она соединяет. Все дороги двухсторонние (то есть по ним можно ездить как в одну, так и в другую сторону), между двумя городами всегда существует не более одной дороги, не существует дорог, ведущих из города в себя.
Формат выходных данных
Требуется вывести одно число – суммарную стоимость маршрута или -1, если добраться невозможно.
| |
![]()
|
|
Домой на электричках
Алгоритм Дейкстры
Одна из команд-участниц олимпиады решила вернуться домой на электричках. При этом ребята хотят попасть домой как можно раньше. К сожалению, не все электрички идут от города, где проводится олимпиада, до станции, на которой живут ребята. И, что еще более обидно, не все электрички, которые идут мимо их станции, останавливаются на ней (равно как вообще, электрички останавливаются далеко не на всех станциях, мимо которых они идут).
Все станции на линии пронумерованы числами от 1 до N. При этом станция номер 1 находится в городе, где проводится олимпиада, и в момент времени 0 ребята приходят на станцию. Станция, на которую нужно попасть ребятам, имеет номер E.
Напишите программу, которая по данному расписанию движения электричек вычисляет минимальное время, когда ребята могут оказаться дома.
Формат входных данных
Во входных данных записаны сначала числа N (2 ≤ N ≤ 100) и E (2 ≤ E ≤ N). Затем записано число M (0 ≤ M ≤ 100), обозначающее число рейсов электричек. Далее идет описание M рейсов электричек. Описание каждого рейса электрички начинается с числа Ki (2 ≤ K ≤ N) — количества станций, на которых она останавливается, а далее следует Ki пар чисел, первое число каждой пары задает номер станции, второе — время, когда электричка останавливается на этой станции (время выражается целым числом из диапазона от 0 до 109). Станции внутри одного рейса упорядочены в порядке возрастания времени. В течение одного рейса электричка все время движется в одном направлении — либо от города, либо к городу.
Формат выходных данных
Выведите одно число — минимальное время, когда ребята смогут оказаться на своей станции. Если существующими рейсами электричек они добраться не смогут, выведите –1.
| |
![]()
|
|
Алгоритм Дейкстры за O(M logN)
Алгоритм Дейкстры
Напишите программу, которая будет находить расстояния в неориентированном взвешенном графе с неотрицательными длинами ребер, от указанной вершины до всех остальных. Программа должна работать быстро для больших разреженных графов.
Формат входных данных
В первой строке входных данных задано число NUM — количество различных запусков алгоритма Дейкстры (на разных графах). Далее следуют NUM блоков, каждый из которых имеет следующую структуру.
Первая строка блока содержит два числа N и M, разделенные пробелом — количество вершин и количество ребер графа. Далее следуют M строк, каждая из которых содержит по три целых числа, разделенные пробелами. Первые два из них в пределах от 0 до N–1 каждое и обозначают концы соответствующего ребра, третье — в пределах от 0 до 20000 и обозначает длину этого ребра. Далее, в последней строке блока, записанное единственное число от 0 до N–1 — вершина, расстояния от которой надо искать.
Количество различных графов в одном тесте NUM не превышает 5. Количество вершин не превышает 60000, рёбер — 200000.
Формат выходных данных
Выведите на стандартный выход (экран) NUM строк, в каждой из которых по Ni чисел, разделенных пробелами — расстояния от указанной начальной вершины взвешенного неориентированного графа до его 0-й, 1-й, 2-й и т. д. вершин (допускается лишний пробел после последнего числа). Если некоторая вершина недостижима от указанной начальной, вместо расстояния выводите число 2009000999 (гарантировано, что все реальные расстояния меньше).
| |
![]()
|
|
Кратчайший путь (AB)
Алгоритм Дейкстры
Вам дано описание дорожной сети страны. Ваша задача – найти длину кратчайшего пути между городами А и B.
Формат входных данных
Сеть дорог задана во входном файле следующим образом: первая строка содержит числа N и K (1<=N<=100000, 0<=K<=300000), где K – количество дорог. Каждая из следующих K строк содержит описание дороги с двусторонним движением – три целых числа ai, bi и li (1aibiN, 1li106). Это означает, что имеется дорога длины li, которая ведет из города ai в город bi. В последней строке находятся два числа А и В – номера городов, между которыми надо посчитать кратчайшее расстояние (1<=A,B<=N )
Формат выходных данных
Вы должны вывести в выходной файл единственное число – расстояние между требуемыми городами. Если по дорогам от города А до города В доехать невозможно, выведите –1.
| |
![]()
|
|
Проложи дорогу
Алгоритм Дейкстры
Правительство некоторой всем известной страны решило глобально перестроить дорожную систему – оно уже успело разрушить все дороги, и теперь нужно выстроить дорожную сеть заново. Новые двусторонние дороги можно строить между любыми двумя городами, и стоимость постройки дороги равна расстоянию между соответствующими городами. Однако в некоторых случаях ландшафт позволяет построить дорогу за другую цену, такие пары городов называются особыми. Правительство решило первым делом соединить два главных города данной страны – А и Б. Вам поручили разработать план постройки дорог, при котором суммарная стоимость всех построенных дорог будет минимально возможной, и при этом по построенным дорогам можно будет добраться из города А в город Б.
Формат входных данных
Первая строка содержит число N – количество городов в стране (\(1\leq N\leq10^4\)). Каждая из последующих N строк содержит по два целых числа, xi и yi – координаты соответствующего города (\(|x|, |y| \leq 10^6\) ). Далее содержится число M – количество особых пар городов (\(0\leq M \leq min(10^4, N(N-1)/2)\). Далее в M строках содержится описание особых дорог, каждое состоит из трех целых чисел: u, v – пара различных городов, между которыми проходит особая дорога, и w – стоимости постройки соответствующей дороги (\(1 \leq u,v \leq N, 0 \leq w \leq 10^6\)). В последней строке содержатся номера городов А и Б (от 1 до N).
Формат выходных данных
Выведите одно число – искомую минимальную длину. Ваш ответ должен отличаться от правильного не более чем на 10−5.
| |
![]()
|
|
Транспортировка
Алгоритм Дейкстры
Бинарный поиск по ответу
К очередной Летней компьютерной школе было решено подготовить кружки как для школьников, так и для всех преподавателей.
Имея привычку делать важные дела в самый последний момент, дизайнер закончил работу над макетом за два дня до начала школы. Ещё день уйдёт у завода-изготовителя на то, чтобы изготовить кружки и нанести на них изображение. Нато, чтобы довезти кружки от завода-изготовителя до ЛКШ,остаётся всего 24 часа.
Заказ на 10000000 экземпляров кружек (а именно столько заказали организаторы), конечно же, за один рейс не увезти. Однако, за первый рейс хочется привезти максимальное количество кружек. Для перевозки был заказан один большегрузный автомобиль. Но есть один нюанс: на некоторых дорогах установлено ограничение на вес автомобиля. Поэтому если автомобиль нагрузить кружками под завязку, то, возможно, не удастся воспользоваться самым коротким маршрутом, а придётся ехать в объезд. Может случиться даже так, что из-за этого грузовик не успеет доехать до лагеря вовремя, а этого допустить никак нельзя. Итак, сколько же кружек можно погрузить в автомобиль, чтобы успеть привезти этот ценный груз вовремя, и не нарушая правил дорожного движения?
Формат входных данных
В первой строке находятся числа n (1≤n≤500) и m - количество узловых пунктов дорожной схемы и количество дорог, соответственно. В следующих m строках находится информация о дорогах. Каждая дорога описывается в отдельной строке следующим образом. Сначала указаны номера узловых пунктов, которые соединяются данной дорогой, потом время, которое тратится на проезд по этой дороге, и, наконец, максимальный вес автомобиля, которому разрешено ехать по этой дороге. Известно, что все дороги соединяют различные пункты, причем для каждой пары пунктов есть не более одной дороги, непосредственно их соединяющей. Все числа разделены одним или несколькими пробелами.
Узловые пункты нумеруются числами от 1 до n. При этом завод по производству кружек имеет номер 1, а ЛКШ - номер n. Время проезда по дороге задано в минутах и не превосходит 1440 (24 часа). Ограничение на массу задано в граммах и не превосходит одного миллиарда. Кроме того, известно, что одна кружка весит 100 грамм, а пустой грузовик - 3 тонны.
Формат выходных данных
Выведите одно число - максимальное количество кружек, которое можно привезти за первый рейс, потратив не более 24часов.
| |
![]()
|
|
Защищенное соединение
Алгоритм Дейкстры
В свете недавних новостей о прослушке каналов связи, два непримиримых интернет-гиганта Урагании <<Laim.UR>> и <<Xenda>> решили подписать соглашение об установлении защищенного канала связи между дата-центрами друг друга. В Урагании \(n\) городов, но, к сожалению, ни в одном городе нет дата-центров обоих гигантов. Поэтому для формирования защищенного канала придется прокладывать междугородние линии связи.
Специалисты компаний определили \(m\) пар городов, которые можно соединить, проложив сегмент канала связи, и оценили стоимость создания такого сегмента для каждой из этих пар.
Результирующий канал может состоять из нескольких сегментов. Он должен начинаться в одном из городов, где находится дата-центр первой компании, может проходить через промежуточные города и должен заканчиваться в городе, где находится дата-центр второй компании.
Теперь необходимо определить минимальную стоимость защищенного канала, соединяющего два дата-центра компаний.
Формат входных данных
В первой строке находятся целые числа \(n\) и \(m\) (\(2 \le n \le 5\,000\), \(1 \le m \le 10^5\)) — количество городов и количество пар городов, которые можно соединить сегментом канала связи.
Во второй строке находятся \(n\) целых чисел \(a_i\) (\(0 \le a_i \le 2\)). Если \(a_i = 0\), то в \(i\)-м городе нет дата-центра ни одного из гигантов. Если \(a_i = 1\), то в \(i\)-м городе есть дата-центр <<Laim.UR>>, а если \(a_i = 2\), то в \(i\)-м городе находится дата-центр <<Xenda>>. Гарантируется, что среди этих чисел есть как минимум одна единица и одна двойка.
В каждой из следующих \(m\) строк находится по три целых числа — \(s_i\), \(t_i\) и \(c_i\), которые означают, что города \(s_i\) и \(t_i\) (\(1 \le s_i, t_i \le n\), \(s_i \ne t_i\)) можно соединить сегментом канала связи стоимостью \(c_i\) (\(1 \le c_i \le 10^5\)). Каждую пару городов можно соединить не более чем одним сегментом канала.
Формат выходных данных
Если соединить защищенным каналом связи два дата-центра разных интернет-гигантов возможно, то выведите в выходной файл три числа: \(x\), \(y\) и \(d\), означающие, что между городами \(x\) и \(y\) возможно провести канал связи суммарной стоимостью \(d\). В городе \(x\) должен находиться дата-центр <<Laim.UR>>, в городе \(y\) — дата-центр <<Xenda>>. Если существует несколько оптимальных ответов, выведите любой. Если провести искомый канал невозможно, выведите \(-1\).
В первом примере оптимально построить канал связи из двух сегментов: \(3-2\) и \(2-4\).
| |
![]()
|
|
Дейкстра
Алгоритм Дейкстры
Дан ориентированный взвешенный граф. Найдите кратчайшее расстояние от одной заданной вершины до другой.
Формат входных данных
В первой строке содержатся три числа: N, S и F (1≤ N≤ 100, 1≤ S, F≤ N), где N – количество вершин графа, S – начальная вершина, а F – конечная. В следующих N строках вводится по N чисел, не превосходящих 100, – матрица смежности графа, где -1 означает отсутствие ребра между вершинами, а любое неотрицательное число – присутствие ребра данного веса. На главной диагонали матрицы записаны нули.
Формат выходных данных
Требуется вывести искомое расстояние или -1, если пути между указанными вершинами не существует.
| |
![]()
|
|
Заправки
Алгоритм Дейкстры
В стране N городов, некоторые из которых соединены между собой дорогами. Для того, чтобы проехать по одной дороге, требуется один бак бензина. В каждом городе бак бензина имеет разную стоимость. Вам требуется добраться из первого города в N-ый, потратив как можно меньшее денег. Покупать бензин впрок нельзя.
Формат входных данных
В первой строке вводится число N (1≤N≤100), в следующей строке идет N чисел, i-ое из которых задает стоимость бензина в i-ом городе (всё это целые числа из диапазона от 0 до 100). Затем идет число M – количество дорог в стране, далее идет описание самих дорог. Каждая дорога задается двумя числами – номерами городов, которые она соединяет. Все дороги двухсторонние (то есть по ним можно ездить как в одну, так и в другую сторону), между двумя городами всегда существует не более одной дороги, не существует дорог, ведущих из города в себя.
Формат выходных данных
Требуется вывести одно число – суммарную стоимость маршрута или -1, если добраться невозможно.
| |
![]()
|
|
Автобусы
Алгоритм Дейкстры
Между некоторыми деревнями края Васюки ходят автобусы. Поскольку пассажиропотоки здесь не очень большие, то автобусы ходят всего несколько раз в день.
Марии Ивановне требуется добраться из деревни d в деревню v как можно быстрее (считается, что в момент времени 0 она находится в деревне d).
Формат входных данных
Сначала вводится число N – общее число деревень (1 <= N <= 100), затем номера деревень d и v, за ними следует количество автобусных рейсов R (0 <= R <= 10000). Далее идут описания автобусных рейсов. Каждый рейс задается номером деревни отправления, временем отправления, деревней назначения и временем прибытия (все времена – целые от 0 до 10000). Если в момент t пассажир приезжает в какую-то деревню, то уехать из нее он может в любой момент времени, начиная с t.
Формат выходных данных
Выведите минимальное время, когда Мария Ивановна может оказаться в деревне v. Если она не сможет с помощью указанных автобусных рейсов добраться из d в v, выведите -1.
| |
![]()
|
|
Файловый менеджер
Алгоритм Дейкстры
Быстрая сортировка
Способы задания графа
Петя работает над очень большим проектом. Проект содержит N файлов. В процессе работы Пете часто приходится просматривать и редактировать файлы. Для ускорения работы Петя использует файловый менеджер Fur Manager, который отображает список имен файлов проекта в некотором порядке.
В текущей версии Fur Manager’a для перемещения по списку имен файлов есть следующие возможности:
можно нажать клавишу вниз, при этом курсор перемещается на следующий файл в списке, для последнего файла следующим считается первый;
можно нажать клавишу вверх, при этом курсор перемещается на предыдущий файл в списке, для первого файла предыдущим считается последний;
можно нажать клавишу Alt и, удерживая ее, набрать последовательность латинских букв. После этого клавишу Alt следует отпустить, и в этот момент курсор переместится на ближайший файл, имя которого начинается c заданной последовательности символов. Ближайший файл — это файл, на который можно переместиться за наименьшее количество нажатий клавиши вниз. Если заданная последовательность является началом имени текущего файла, или файла, имя которого начинается с этой последовательности, не существует, то курсор останется на месте.
Первая и вторая из описанных возможностей файлового менеджера требуют по одному нажатию клавиши, а третья — одного нажатия (нажатие клавиши Alt) плюс количество нажатий, равное длине набранной последовательности латинских букв.
Файлы пронумерованы от 1 до N в порядке их следования. После загрузки Fur Manager’а курсор находится на первом файле.
Петя знает, что ему сначала придется редактировать файл с номером a1, затем с номером a2 и так далее, а последним — файл с номером ak. В последовательности a1, a2, ..., ak один и тот же номер может встречаться несколько раз. При каждом перемещении от одного файла к другому Петя хочет нажимать как можно меньше клавиш.
Требуется написать программу, которая выдает искомую последовательность нажатий клавиш.
Входные данные
В первой строке входных данных содержится целое число N (1 ≤ N ≤ 1000) — количество файлов в проекте.
В следующих N строках записаны имена файлов, по одному в каждой строке. Файлы перечислены в том порядке, в котором они отображаются файловым менеджером. Имена состоят только из строчных латинских букв. Длина каждого имени не превосходит 2000 символов. Все имена файлов различны.
Далее в следующей строке записано целое число k (1 ≤ k ≤ 10).
Последняя строка входных данных содержит k целых чисел a1, a2, ..., ak (1 ≤ ai ≤ N) — номера редактируемых файлов. Редактирование файлов выполняется в том порядке, в котором они встречаются в последовательности a1, a2, ..., ak.
Выходные данные
Выведите описание искомой последовательности нажатий клавиш в виде k блоков информации:
первый блок информации описывает перемещение от файла с номером 1 к файлу с номером a1;
второй блок информации описывает перемещение от файла с номером a1 к файлу с номером a2;
…
k-ый блок информации описывает перемещение от файла с номером ak–1 к файлу с номером ak.
Каждый блок информации выглядит следующим образом.
В первой строке блока записывается число L — наименьшее количество нажатий клавиш, необходимое для перемещения от очередного файла последовательности к следующему.
Следующие L строк блока описывают нажимаемые клавиши. Каждая из строк содержит описание одной клавиши:
если нажимается клавиша вниз, то в строке записывается слово down;
если нажимается клавиша вверх, то в строке записывается слово up;
если нажимается клавиша Alt, то в строке записывается слово Alt;
при нажатии клавиши с латинской буквой выводится соответствующая ей латинская буква.
Если существует несколько оптимальных способов перемещения, то требуется вывести любой из них.
| Ввод |
Вывод |
|
6
a
b
c
d
e
f
4
4 3 1 6
|
2
Alt
d
1
up
2
Alt
a
1
up
|
| |
![]()
|
|
В школу на велосипеде
Алгоритм Дейкстры
Элементарная геометрия
Петя любит ездить в школу на велосипеде. Но ездить на велосипеде по тротуарам запрещено, а ездить по дороге опасно. Поэтому Петя ездит только по специальным велосипедным дорожкам. К счастью, и Петин дом, и Петина школа находятся в непосредственной близости от таких дорожек.
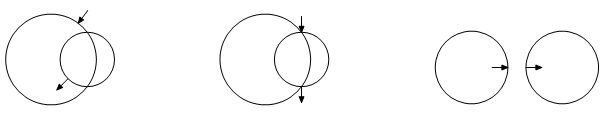
В городе, где живет Петя, есть ровно две велосипедных дорожки. Каждая дорожка имеет форму окружности. В точках их пересечения можно переехать с одной дорожки на другую.
Петя знает точку, в которой он заезжает на дорожку, и точку, в которой следует съехать, чтобы попасть в школу. Петю заинтересовал вопрос: какое минимальное расстояние ему следует проехать по дорожкам, чтобы попасть из дома в школу.
Входные данные
Будем считать, что в городе введена прямоугольная декартова система координат.
Первые две строки входных данных описывают велосипедные дорожки. Каждая из них содержит по три целых числа – координаты центра окружности, которую представляет собой соответствующая дорожка, и ее радиус. Координаты и радиус не превышают 200 по абсолютной величине, радиус – положительное число. Гарантируется, что дорожки не совпадают.
Следующие две строки содержат по два вещественных числа – координаты точки, где Петя заезжает на дорожку, и точки, в которой Петя съезжает с дорожки. Гарантируется, что каждая из точек с высокой точностью лежит на одной из дорожек (расстояние от точки до центра одной из окружностей отличается от ее радиуса не более, чем на 10-8). Точки могут лежать как на одной дорожке, так и на разных.
Выходные данные
Выведите минимальное расстояние, которое следует проехать Пете по велосипедным дорожкам, чтобы попасть из дома в школу. Ответ должен отличаться от правильного не более, чем на 10-4.
Если доехать из дома до школы по велосипедным дорожкам невозможно, выведите число -1.
| |
![]()
|
|
Военный поход
Алгоритм Дейкстры
В одном феодальном государстве средневековой Европы было \(n\) городов и \(m\) дорог, каждая из которых соединяла некоторые два города. Каждая дорога принадлежала правителю одного из городов (не обязательно одного из тех, которые она соединяла). Однажды правитель города S решил объявить войну правителю города T. Перед ним сразу же встала нелегкая задача: как довести армию до города T.
Правитель каждого города требует плату за проход войск через его город. Кроме того, правитель города S может перемещать войска только по дорогам, которые принадлежат ему. При этом он может купить любую дорогу у ее владельца за определенную плату (даже если владелец — правитель города T). К сожалению, все деньги из казны города S были потрачены на предыдущий неудачный военный поход, поэтому сначала правителю придется продать некоторые свои дороги (разумеется, после этого он не сможет провести по ним войска).
Помогите правителю выяснить, какие дороги следует продать, а какие купить, чтобы довести войска от города S до города T и оплатить проход через все промежуточные города. Все операции продажи и покупки дорог надо осуществить до начала похода, пока правители других городов не догадались о воинственных намерениях правителя города S.
Формат входных данных
Первая строка содержит целые числа \(n\) и \(m\) — количество городов и дорог соответственно (\(2 \le n \le 2\,000\), \(1 \le m \le 50\,000\)). Города нумеруются от 1 до \(n\), города S и T имеют номера 1 и \(n\) соответственно.
Следующие \(n\) строк содержат под одному целому числу \(r_i\) — плату за проезд через город \(i\) (\(0 \le r_i \le 10\,000\), \(r_1 = r_n = 0\)).
Следующие \(m\) строк содержат описания дорог. Дорога описывается четырьмя целыми числами: \(a_i\), \(b_i\), \(p_i\) и \(c_i\). Здесь \(a_i\) и \(b_i\) — номера городов, которые соединяет дорога, \(p_i\) — номер города, правителю которого она принадлежит, \(c_i\) — ее стоимость (\(a_i \ne b_i\), \(1 \le c_i \le 10\,000\)). По дороге можно перемещаться в обоих направлениях. Любые два города соединены не более чем одной дорогой.
Формат выходных данных
На первой строке выведите список дорог, которые нужно продать в следующем формате: сначала число дорог, а затем их номера. Дороги нумеруются с единицы в том порядке, в котором они заданы во входных данных. На второй строке выведите список дорог, которые нужно купить, в том же формате. На третьей строке выведите маршрут похода — номера городов в порядке следования войска. Если решений несколько, выведите любое.
Если решения нет, выведите в выходной файл число \(-1\).
| |
![]()
|
|
Свет
Алгоритм Дейкстры
Элементарная геометрия
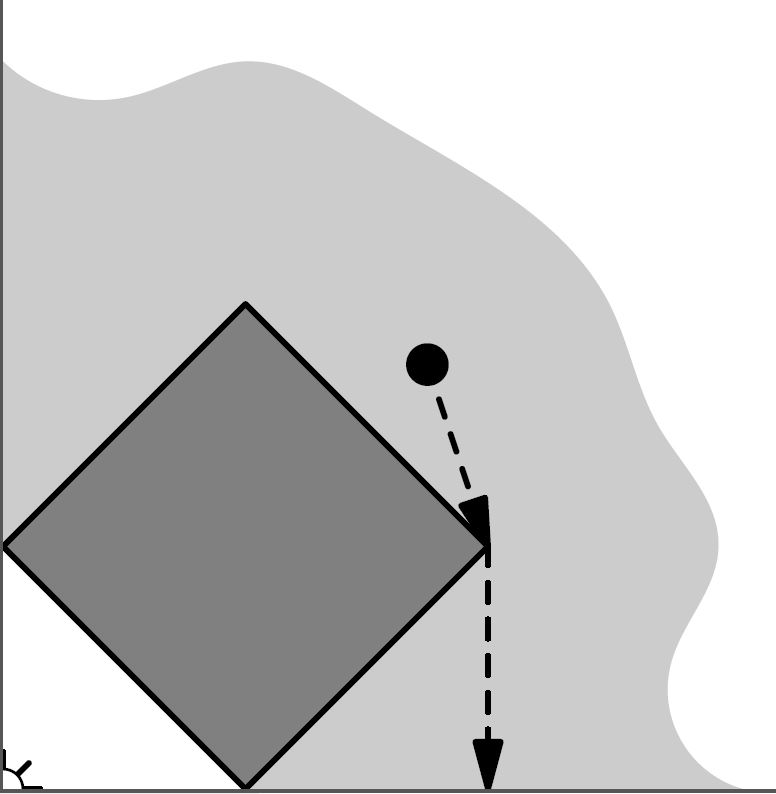
В точке (0, 0) координатной плоскости расположена лампочка, которая представляет собой точечный источник света. Неподалеку от лампочки находится дом Пети, который представляет собой выпуклый многоугольник с N вершинами. Сам Петя находится в точке с координатами (x, y).
Петя хочет увидеть свет. Для этого ему необходимо оказаться в такое точке, что отрезок, соединяющей ее с началом координат, не пересекается с домом Пети (но может его касаться, в частности, проходить вдоль стороны многоугольника дома).
Петя может перемещаться по плоскости со скоростью v. Разумеется, Петя не может проходить сквозь дом (хотя он может двигаться по его границе).
Выясните, какое минимальное время требуется Пете, чтобы оказаться в освещенной точке.
Входные данные
В первой строке вводятся координаты Пети – два неотрицательных вещественных числа, не превышающих 1000, и его скорость v – вещественное число, 10-2≤ v≤ 104.
Вторая строка содержит N – число вершин в многоугольнике, задающем Петин дом ( 3≤N≤100). Далее в N строках вводится по два вещественных числа – координаты вершин многоугольника в порядке их обхода против часовой стрелки. Все координаты неотрицательны и не превышают 1000.
Гарантируется, что входные данные корректны, в частности, многоугольник выпуклый, и никакие три его последовательные вершины не лежат на одной прямой. Также гарантируется, что и Петя, и лампочка находятся снаружи от многоугольника, в частности, не находятся на его границе. Расстояние от точки, где находится Петя, до многоугольника и от начала координат до многоугольника не меньше 10-2, расстояние от Пети до начала координат не меньше 10-2.
Выходные данные
Выведите минимальное время, за которое Петя сможет попасть в освещенную точку. Ваш ответ должен отличаться от правильного не более чем на 10-4.
| |
![]()
|
|
Витрина
Алгоритм Дейкстры
Обход в ширину
Зал супермаркета имеет форму прямоугольника размером M x N, в котором расставлены витрины размером 1 x 1. Стороны витрин параллельны стенам супермаркета, а расстояния от витрин до стен – целые числа.
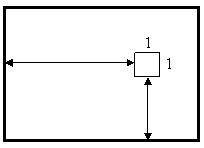
В супермаркет привезли новую супервитрину размером K x 1 и выгрузили в одном из углов супермаркета. Требуется передвинуть ее в противоположный угол супермаркета. При этом ее нельзя поворачивать, а можно лишь передвигать параллельно стенам супермаркета. Напишите программу, которая по плану супермаркета поможет определить, какое наименьшее количество витрин нужно убрать, чтобы передвинуть супервитрину.

Входные данные
В первой строке вводятся три натуральных числа M, N и K (M, N ≤ 100, K ≤ M). Начальное и конечное расположение супервитрины такие, как указано на верхнем рисунке. В следующей строке записано целое неотрицательно число V – количество витрин (0 ≤ V ≤ N*M). В следующих V строках входных данных содержатся различные пары целых неотрицательных чисел, характеризующие положения витрин. Первое число (от 0 до M–1) – расстояние от левой стены супермаркета до витрины, второе (от 0 до N–1) – расстояние от нижней стены до витрины (см. нижний рисунок). Гарантируется, что там, где изначально поставили супервитрину, других витрин нет.
Выходные данные
В первой строке выведите минимальное количество витрин, которые необходимо убрать. Во второй строке выведите возможный маршрут передвижения супервитрины: одну строку из заглавных латинских букв, обозначающих следующее:
U – на 1 вверх,
D – на 1 вниз,
L – на 1 влево,
R – на 1 вправо.
Количество символов в строке не должно превышать N x M
.
Если возможных маршрутов несколько, то выведите любой из них.
| |
![]()
|
|
Левый лабиринт
Динамическое программирование на таблицах
Алгоритм Дейкстры
Обход в ширину
В спортзале размером NxM метров построили современный аттракцион под названием "Левый лабиринт". Для этого на полу спортзала с интервалом в 1 метр начертили линии, параллельные стенам спортзала. Таким образом, спортзал разбили на NxM клеток. Дальше некоторые из этих клеток покрасили в черный цвет.
Аттракцион заключается в том, что участника ставят в некоторой клетке спортзала и просят как можно быстрее добежать до некоторой другой клетки. При этом накладываются следующие условия:
- Участнику запрещено ходить по черным клеткам.
- Придя в какую-то клетку, участник может пойти либо прямо, либо налево, либо направо (если в соответствующем направлении клетка не покрашена в черный цвет): ходить назад, а также ходить по диагонали запрещается.
- За все время пути участнику разрешается повернуть направо (то есть пойти из текущей клетки направо относительно того, откуда он пришел в данную клетку) не более K раз.
- В начальной клетке участник может встать лицом в ту сторону, в какую ему захочется. С какой стороны участник прибежит в конечную клетку также не важно.
Известно, что на то, чтобы перебежать из клетки в соседнюю, участник тратит ровно 1 секунду. Требуется вычислить минимальное время, за которое участник сможет достичь конечной клетки.
Входные данные
Во входном файле сначала записано число K — количество разрешенных поворотов направо (целое число из диапазона от 0 до 5), затем записаны числа N и M, задающие размеры спортзала — натуральные числа, не превышающие 20. Далее записано N строк по M чисел в каждой. Число 0 обозначает непокрашенную клетку, число 1 — покрашенную, число 2 — клетку, откуда стартует участник и число 3 — клетку, куда нужно добежать (клетки, помеченные 2 и 3 являются непокрашенными). В лабиринте всегда есть ровно одна начальная клетка и ровно одна клетка, в которую нужно попасть.
Выходные данные
В выходной файл выведите минимальное время, за которое можно добраться в конечную клетку. Если попасть в конечную клетку с соблюдением всех условий нельзя, выведите –1.
| |
![]()
|
|
Олимпиада по алхимии
Алгоритм Дейкстры
В государстве алхимиков есть N населённых пунктов, пронумерованных числами от 1 до N, и M дорог. Населённые пункты бывают двух типов: деревни и города. Кроме того, в государстве есть одна столица (она может располагаться как в городе, так и в деревне). Каждая дорога соединяет два населённых пункта, и для проезда по ней требуется Ti минут. В столице было решено провести 1-ю государственную командную олимпиаду по алхимии. Для этого во все города из столицы были отправлены гонцы (по одному гонцу на город) с информацией про олимпиаду.
Напишите программу, которая посчитает, в каком порядке и через какое время каждый из гонцов доберётся до своего города. Считается, что гонец во время пути не спит и нигде не задерживается.
Входные данные
Во входных данных сначала записаны 3 числа N, M, K — количество населенных пунктов, количество дорог и количество городов (2≤N≤1000, 1≤M≤10000, 1≤K≤N). Далее записан номер столицы C (1≤C≤N). Следующие K чисел задают номера городов. Далее следуют M троек чисел Si, Ei, Ti, описывающих дороги: Si и Ei — номера населенных пунктов, которые соединяет данная дорога, а Ti — время для проезда по ней (1≤Ti≤100).
Гарантируется, что до каждого города из столицы можно добраться по дорогам (возможно, через другие населенные пункты).
Выходные данные
Выведите K пар чисел: для каждого города должен быть выведен его номер и минимальное время, когда гонец может в нем оказаться (время измеряется в минутах с того момента, как гонцы выехали из столицы). Пары должны быть упорядочены по времени прибытия гонца.
| |
![]()
|
|
66169
Алгоритм Дейкстры
Одна очень известная компания Я&Ко захотела создать сеть доставок из ресторанов и кафе по всему городу, притом доставку производили бы мини-поезда. Главной проблемой стала логистика – как добраться из точки отправления в точку назначения самым быстрым способом. Но так как мини-поезда представляли собой только прототип, то в них был очень плохо проработан аккумулятор, что заставило компанию подумать про эту проблему тщательнее.
Я&Ко решили проложить рельсы между всеми точками доставки и по некоторым рельсам пустить зарядку, чтобы мини-поезда могли ехать и заряжаться. Компания решила устроить среди всех программистов, кто сможет решить их задачу, соревнование. Далее выбрать победителя, но как, пока неизвестно.
Задача состоит в следующем – есть известная карта маршрутов в городе, которая представлена в виде направленного взвешенного графа с возможными циклами. На каждом ребре графа даны значения времени перемещения между связанными вершинами и заряжает рельс или нет на этом маршруте.
За 1 минуту по рельсам зарядки мини-поезд заряжается на 10%. Если он зарядился, но всё ещё в пути на зарядных рельсах, то его заряд составляет 100%.
Для простоты расчёта количество минут мини-поезда после съезда с рельсов округляется вверх к ближайшему целому (например, поезд максимально может проехать 30 минут, что означает его 100% заряда, на рельс он заехал, когда у него осталось заряда на 10 минут, пусть время в пути по рельсу составило 4 минуты, значит зарядился он на 40%, что составляет 12 минут, потому после съезда с зарядного рельса у него останется запас хода на 10 + 12 = 22 минуты.
Задача – найти минимальное время, за которое мини-поезд сможет доехать до клиента со стартовой точки, если точно известно, что он это сделать сможет.
Входные данные
на первой строке подаются два целых числа (1 <= N,M <= 1000), где N – количество вершин графа, M - количество рёбер.
на второй строке подаётся целое число T (1 <= T <= 100), где T – время, которое может проехать полностью заряженный мини-поезд;
на третьей строке подаются через пробел два целых числа – номер стартовой вершины и номер конечной вершины;
далее на M строках подаются рёбра графа через пробел с указанием зарядный рельс на данном пути или нет (0 – не зарядный, 1 – зарядный) (<откуда> <куда> <время в пути> <признак зарядного рельса>).
Выходные данные
выведите на первой строке количество минут, которое понадобится мини-поезду, чтобы полностью доехать до клиента (конечной точки) в виде одного целого числа.
Примечание
•робот изначально заряжен на 100%.
| |
![]()
|