| | | |
|
Игра в камушки
Игры и выигрышные стратегии
Маша и Даша играют в игру с N (\(1<=N<=10^5\)) кучками камушков, где i-ая кучка содержит ai камешков (\(1<=i<=N\), \(1<=a_i<=10^6\)). Они ходят по очереди, первой ходит Маша.
- Сначала Маша выбирает некоторое положительное число
s1 и удаляет s1 камешков из некоторой кучки, в которой есть не менее s1 камешков.
- Затем Даша выбирает некоторое положительное число
s2 такое, что s2 делится на s1 и удаляет s2 камешков из некоторой кучки, содержащей не менее s2 камешков.
- Затем Маша выбирает некоторое положительное число
s3, которое делится на s2 и удаляет s3 камешков из некоторой кучки, в которой есть не менее s3 камешков.
- В общем случае
si, количество камешков, которое убирается на ходу i, должно быть делителем si+1.
Проигрывает тот, кто не может сделать ход.
Вычислите количество способов, которыми Маша может удалить камешки на первом ходу для того, чтобы гарантировать себе победу (то есть существет стратегия, используя которую Маша победит вне зависимости от ходов Даши). Два способа удаления камешков называются различными, если они удаляют различное количество камушков или они удаляют камешки из различных кучек.
Входные данные
Первая строка содержит N.
Вторая строка содержит N разделённых одиночными пробелами целых чисел a1,…,aN.
Выходные данные
Выведите количество способов, которыми Маша может удалить камушки на первом ходу, чтобы гарантировать себе выигрыш.
Для вычислений используйте 64-ное целое например, "long long" в C/C++.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
1
7 |
4 |
Маша выбирает 4, 5, 6, 7 камушков из одной кучи и игра закончится сразу. |
| 2 |
6
3 2 3 2 3 1 |
8 |
Маша выиграет, если удалит 2 или 3 камушка из любой кучи. Затем игроки будут по очереди брать одно и то же количество камушков, но Маша сделает последний ход. |
| |
![]()
|
|
LinkedList's Bizarre Adventure
Игры и выигрышные стратегии
Простые игры
Древовидные структуры данных
В двусвязном списке, он же LinkedList, каждый элемент может быть связан максимум с двумя другими элементами — с предыдущим элементом (если он есть) и со следующим элементом (если он есть).
Билли и Рикардо проходят стажировку в компании FlexDex в группе поддержки внутреннего анонимного форума с возможностью деанонимизации. Для представления последовательных сообщений в теме необходимо использовать список, где элементами будут являться эти сообщения, и два товарища решили написать свою быструю реализацию двусвязного списка FlexList.
Но у них что-то пошло не так — в их списке новое сообщение может связываться не только с первым или последним сообщением, как должно быть, а с любым из уже существующих сообщений.
Если представить каждое сообщение как вершину графа, а связи между сообщениями как ребра графа, то гарантируется, что этот граф будет неориентированным, связным и ацикличным.
Говорится, что граф является корректным графом, если в этом графе у каждой вершины не более двух вершин, связанных с ней ребром. Изначально же FlexList связи между сообщениями могут выглядеть в виде любого связного ацикличного графа, не обязательно корректного.
Билли и Рикардо не растерялись и решили, что будут вручную исправлять все неясности в ходе работы программ, которые используют их изобретение. Тимлид дал им тестовый пример для проверки кода. Они получили на этом примере граф связей и вручную делают из него корректный граф, ведь связи между сообщениями в корректном двусвязном списке могут представлять собой только корректный граф.
Это выглядит так — сначала Билли проверяет, что граф корректный. Если это не так, то он выбирает и удаляет некоторый лист (вершина, у которой есть ровно одна связь с другими вершинами), и отдает граф Рикардо, затем Рикардо делает то же самое и отдает граф Билли, и так продолжается до тех пор, пока кто-то не получит от товарища корректный граф. Как только один из двух друзей получает такой граф, то тут же показывает его тимлиду, с надеждой на похвалу и повышение в должности.
Каждый хочет получить первым такой граф. Кто первым попадет к тимлиду, если оба товарища удаляют листья оптимально для себя?
Входные данные
В первой строке содержится одно целое число n (1 ≤ n ≤ 300000) — число сообщений в примере тимлида. Следующие n−1 строк задают связи между сообщениями. Каждая из них содержит два целых числа ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi), которые показывают, что сообщения с номерами ai и bi связаны.
Выходные данные
Выведите "Billy" (без кавычек), если первым попадет к тимлиду Билли, иначе выведите "Ricardo" (без кавычек).
Примечание
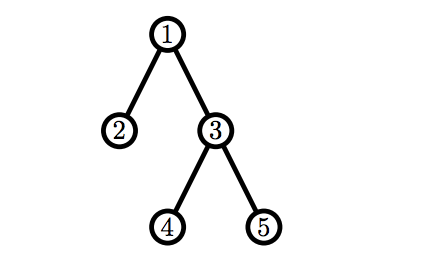
В первом примере Билли первым ходом может удалить одну из вершин с номерами 2, 4 или 5, так как они являются листьями. Он не будет удалять вершину с номером 4 или 5, так как в таком случае он передаст Рикардо корректный граф и проиграет. Значит, он удалит вершину 2. В свою очередь, Рикардо может удалить вершины 1, 4 или 5, и, в любом случае, Билли получит от него корректный граф.
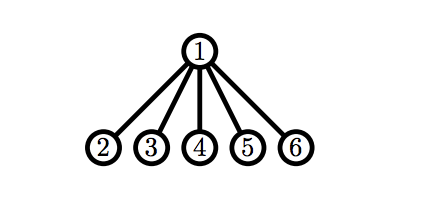
Во втором примере у Билли сразу есть корректный граф.
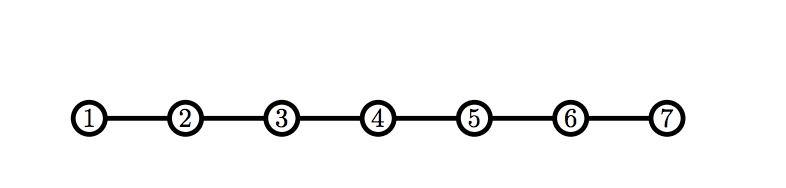
В третьем примере можно показать, что вне зависимости от ходов Билли, Рикардо получит корректный граф первым.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 2
1 3
3 4
3 5 |
Billy |
| 2 |
7
1 2
2 3
3 4
4 5
5 6
6 7 |
Billy |
| 3 |
6
1 2
1 3
1 4
1 5
1 6 |
Ricardo |
| |
![]()
|
|
Игра со строками
Бор
Обход в глубину
Игры и выигрышные стратегии
Дана игра для двоих игроков со строками.
Задан набор, состоящий из n непустых строк. Во время игры два игрока вместе строят слово, изначально это слово пустое. Игроки ходят по очереди. За свой ход игрок должен дописать в конец слова одну букву так, чтобы полученное слово было префиксом хотя бы одной строки из заданного набора. Проигрывает тот, кто не может сделать ход.
По задданому набору строк определите, кто будет победителем, если оба игрока будут играть оптимально.
Входные данные:
Первая строка содержит целое число n (1 ≤ n ≤ 105).
Каждая из n следующих строк содержит непустую строку из заданного набора. Суммарная длина всех строк из набора не превышает 105. Все строки из набора состоят только из строчных латинских букв.
Выходные данные:
Если победит игрок, который ходит первым, то выведите «First», иначе выведите «Second» (кавычки выводить не нужно).
Примеры:
| Входные данные |
Выходные данные |
3
a
b
c |
First |
1
ab |
Second |
| |
![]()
|
|
Сетевая игра
Игры и выигрышные стратегии
Петя и Вася нашли на чердаке остатки рыболовной сети своего деда. Часть веревок давно сгнила, и сеть распалась на большое число кусков, каждый из которых состоит не более чем из 50 веревочек единичной длины.
Так как использовать по назначению остатки данной сети было уже нельзя, братья разложили один из найденных кусков на прямоугольном столе так, что веревочки оказались параллельны сторонам стола, и стали играть в следующую игру.
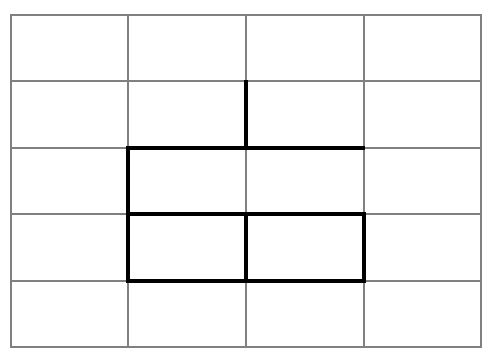
Братья делают ходы по очереди, Петя ходит первым. Своим ходом игрок находит веревочку, являющуюся стороной некоторой целой единичной квадратной ячейки сети (все четыре образующие ее веревочки целы), и перерезает выбранную веревочку. Проигрывает тот из братьев, который не может сделать очередной ход.Требуется написать программу, которая по описанию куска сети на столе определяет, может ли Петя выиграть при любой игре Васи, и если да, то какой первый ход он должен для этого сделать.
Формат входных данных
В первой строке входных данных задается число N (1 ≤ N ≤ 50) — количество веревочек единичной длины, из которых состоит кусок сети. Следующие N строк содержат по две пары целых чисел — координаты концов веревочек. Каждая четверка чисел описывает отрезок единичной длины, параллельный одной из осей координат.
Координаты всех точек неотрицательны и не превосходят 50.
Формат выходных данных
Первая строка выходных данных должна содержать число 1, если Петя может выиграть при любой игре Васи, и число 2, если нет. В случае выигрыша Пети вторая строка должна содержать номер веревочки, которую он должен перерезать первым ходом. Если возможных выигрышных ходов несколько, выведите любой. Веревочки пронумерованы, начиная с 1, в том порядке, в котором они заданы во входных данных.
Примечание
В примере во второй строке выведено два числа. Это сделано для иллюстрации того, какие именно веревочки можно разрезать. Вам требуется вывести любую одну из них.
| |
![]()
|