Перестановка

У Беси есть N (3≤N≤40)любимых точек на 2D-решётке, никакие три из которых не коллинеарны. Для каждого 1≤i≤N, i-ая точка задаётся двумя целочисленными координатами x_i и y_i (0≤x_i,y_i≤10⁴).
Беси рисует некоторые отрезки между точками следующим образом:

Она выбирает некоторую перестановку p₁,p₂,…,p_N из N точек
Она рисует отрезки между p₁ и p₂, p₂ и p₃, p₃ и p₁.
Затем для каждого целого i от 4 до N по порядку, она рисует отрезки прямых от p_i до p_j для всех j<i так, этот отрезок не пересекает никакой из ранее нарисованных отрезков (вне конечных точек)
Беси заметила, что для каждого i она нарисовала ровно три новых отрезка. Вычислите количество перестановок, которые Беси могла выбрать на шаге 1, которые удовлетворяют этому свойству по модулю 10⁹+7.

Входные данные: 
Первая строка содержит N.
Каждая из последующих N строк содержит два разделённых пробелом целых числа x_i и y_i.

Выходные данные: 
Количество перестановок по модулю 10⁹+7.
 

Примеры

№	Входные данные	Выходные данные	Пояснение
1	4 0 0 0 4 1 1 1 2	0	Никакая перестановка не сработает.
2	4 0 0 0 4 4 0 1 1	24	Все перестановки работают.
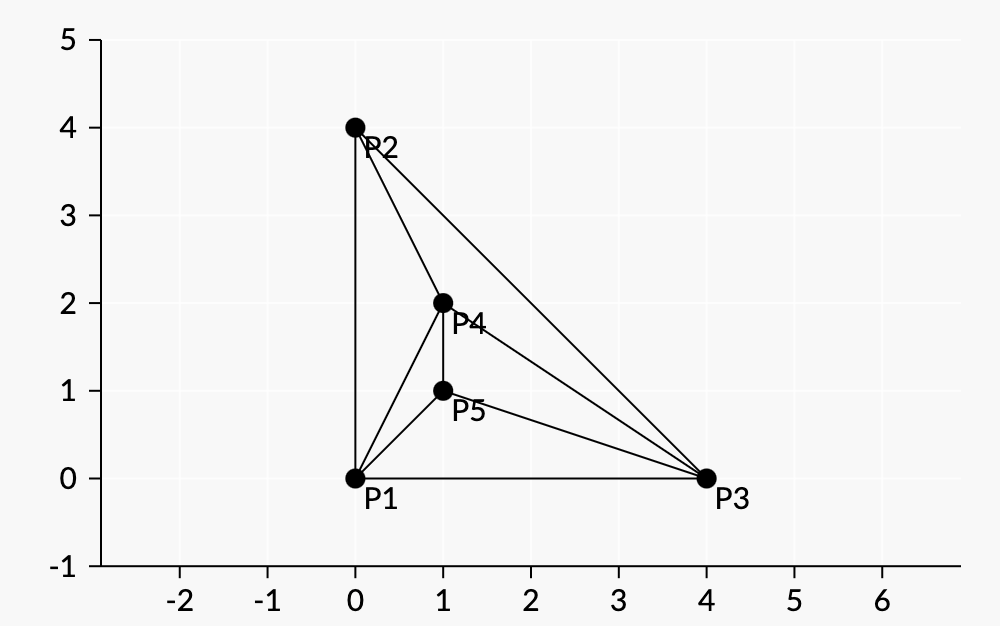
3	5 0 0 0 4 4 0 1 1 1 2	96	Одна из перестановок, удовлетворяющих свойству - (0,0),(0,4),(4,0),(1,2),(1,1). Для этой перстановки Сначала она рисует отрезки между каждой парой (0,0),(0,4), и (4,0). Затем она рисует отрезки от (0,0), (0,4), и (4,0) до (1,2). Наконец, она рисует отрезки от (1,2), (4,0), и (0,0) до (1,1). Рисунок: Перестановка не удовлетворяет свойству, если её первые четыре точки (0,0)(0,0), (1,1)(1,1), (1,2)(1,2), и (0,4)(0,4) в некотором порядке.

MTN DEW

Примеры

Опасные отходы

Счетовод - 1

У исполнителя Счетовод две команды, которым присвоены номера:
1. прибавь A
2. умножь на B
Программа для Счетовода – это последовательность команд. Сколько есть программ, которые число S преобразуют в число F?
Гарантируется, что имеется хотя бы одна программа, которая получает из числа S число F.

Входные данные
Программа получает на вход четыре числа: A, B, S, F (1 <= A, B <= 10, 1 <= S <= 100, 1 <= F <= 10³)

Выходные данные
Выведите ответ на задачу. Гарантируется, что ответ не превышает 263.
 

Примеры

Счетовод - 3

У исполнителя Счетовод три команды, которым присвоены номера:
1. прибавь A
2. прибавь B
3. умножь на С
Программа для Счетовода – это последовательность команд. Сколько есть программ, которые число S преобразуют в число F?
Гарантируется, что имеется хотя бы одна программа, которая получает из числа S число F.

Входные данные
Программа получает на вход четыре числа: A, B, С, S, F (1 <= A, B, C <= 10, 1 <= S <= 10, 1 <= F <= 100, A и B - различные числа)

Выходные данные
Выведите ответ на задачу. Гарантируется, что ответ не превышает 263.
 

Примеры

Счетовод - 5

У исполнителя Счетовод две команды, которым присвоены номера:
1. прибавь 1
2. увеличь каждый разряд числа на 1

Первая команда увеличивает число на 1, вторая - увеличивает каждый разряд числа на 1, если он не равен 9. 
Например, число 45 с помощью команды 2 превратится в 56, а 49 в 59 (так как младший разряд равен 9 и он остается без изменений).
Программа для Счетовода – это последовательность команд.
Сколько существует программ, которые число S преобразуют в число F? 


Входные данные
Программа получает на вход два числа (каждое число записано в отдельной строке): S и F ( 1 <= S <= 100, 10 <= F <= 1000, S < F). 

Выходные данные
Выведите ответ на задачу. Гарантируется, что ответ не превышает 263.
 
 

Примеры

Счетовод - 6

У исполнителя Счетовод две команды, которым присвоены номера:
1. прибавь A
2. прибавь B
3. умножь на С
Первая из них увеличивает на A число на экране, вторая увеличивает число на экране на B, третья умножает число на экране на С. Программа для Счетовода – это последовательность команд. Сколько существует таких программ, которые исходное число S преобразуют в число F и при этом траектория вычислений программы содержит число num1 и число num2?

Гарантируется, что имеется хотя бы одна программа, которая получает из числа S число F, A не равно B.

Входные данные
Программа получает на вход семь чисел в следующем порядке: A, B, C, S, F, num1, num2 (1<= A,B,C <= 10, 1 <= S <= 100, 1 <= F <= 10³, S <= num1 < num2 <= F). Каждое число вводится с новой строки.

Выходные данные
Выведите ответ на задачу. Гарантируется, что ответ не превышает 263.
 

Примеры

Счетовод - 8

У исполнителя Счетовод две команды, которым присвоены номера:
1. прибавь A
2. умножь на B
3. умножь на С
Первая из них увеличивает на A число на экране, вторая умножает число на экране на B, третья умножает число на экране на С. Программа для Счетовода – это последовательность команд. Сколько существует таких программ, которые исходное число S преобразуют в число F и при этом траектория вычислений программы содержит число num и не содержит число misnum?

Гарантируется, что имеется хотя бы одна программа, которая получает из числа S число F, B не равно C.

Входные данные
Программа получает на вход семь чисел в следующем порядке: A, B, C, S, F, num, misnum (1<= A <= 10, 2 <= B,C <= 10, 1 <= S <= 100, 1 <= F <= 10³, S <= num < misnum <= F). Каждое число вводится с новой строки.

Выходные данные
Выведите ответ на задачу. Гарантируется, что ответ не превышает 263.
 

Примеры

Рекурсия итеративно - 2

Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 7, если n < 7,
F(n) = n + 1 + F(n­ –2), если n ≥ 7.

По заданным числам A и B вычислите значение выражения F(A) – F(B)?

Входные данные
А и B вводятся с клавиатуры (2000 <= A, B <= 5000). Каждое число в отдельной строке.

Выходные данные
Выведите ответ на задачу.
 

Примеры

Средняя последовательность

Рассмотрим неубывающую последовательность s₁, ..., s_n + 1 ( s_i <= s_i + 1 для 1 <= i <= n ). Последовательность m₁, ..., m_n, в которой каждый член определен как m_i = ½ * ( s_i + s_i + 1 ) для 1 <= i <= n, назовем “средней последовательностью” для последовательности s₁, ... s_n + 1. Например, средняя последовательность для последовательности 1, 2, 2, 4 есть 1.5, 2, 3. Заметим, что элементы средней последовательности могут быть дробными числами. Тем не менее, в данной задаче используются только те средние последовательности, в которых все числа целые. Для заданной неубывающей последовательности из n целых чисел m1, ..., mn необходимо вычислить количество всех неубывающих последовательностей из n + 1 целых чисел s₁, ..., s_n + 1, для которых заданная последовательность m₁, ..., m_n является средней последовательностью.

Задание
Напишите программу, которая:

• читает из стандартного ввода неубывающую последовательность целых чисел;
• вычисляет количество всех неубывающих последовательностей целых чисел, для которых заданная последовательность является средней последовательностью;
• выводит ответ в стандартный вывод.

Входные данные
Первая строка стандартного ввода содержит одно целое число n (2 <= n <= 5000000). Оставшиеся n строк содержат значения последовательности m₁, ..., m_n. Строка i + 1 содержит одно целое число mi (0 <= mi <= 1000000000).

Выходные данные
Ваша программа должна вывести в стандартный вывод ровно одно целое число – количество всех неубывающих последовательностей целых чисел, для которых входная последовательность является средней последовательностью.

Простая последовательность

Вычислите n-й член последовательности, заданной формулами:

a_2n = a_n + a_n-1,
a_2n+1 = a_n – a_n-1,
a₀ = a₁ = 1.

Входные данные
Вводится одно натуральное число n (1≤n≤1000).

Выходные данные
Вывести одно число a_n.

Треугольник Паскаля

Треугольник Паскаля строится следующим образом. Первая строка состоит из одного числа, равного единице. Каждая следующая содержит на одно число больше, чем предыдущая. Первое и последнееиз этих чисел равны 1, а все остальные вычисляются как сумма числа, стоящего в предыдущей строке над ним и числа, стоящего в предыдущей же строке слева от него.

Входные данные
Вводится одно число N (0<=N<=30).

Выходные данные
Вывести N строк треугольника Паскаля (числа выводятся через пробел).

Непизанские кролики (2024-2025, 11)

Дана блок-схема алгоритма, реализованного в виде рекурсивно вызываемой функции:

Известно, что 𝐴, 𝐵 и 𝐶 - натуральные числа и что 𝐴 < 𝐵 < 𝐶.
Петя вызывает эту функцию, передавая ей в качестве входного параметра натуральное число. Известно, что для некоторого 𝑘 функция возвращает следующие значения:
𝐹(𝑘) = 50890368413;
𝐹(𝑘 + 1) = 93601980590;
𝐹(𝑘 + 2) = 172160883161.
Определите значения 𝐴, 𝐵 и 𝐶, при которых это возможно. Если таких вариантов несколько, выберите вариант с наименьшей суммой 𝐴, 𝐵 и 𝐶. В ответе введите в указанном порядке значения 𝐴, 𝐵 и 𝐶, разделённые пробелом.
 

Moo

Коровы придумали новую игру “Moo”. Они стоят в ряд, где каждая корова отвечает за то, чтобы назвать конкретную букву как можно быстрей.
Последовательность букв определена до бесконечности. Ее начало представлено ниже:
m o o m o o o m o o m o o o o m o o m o o o m o o m o o o o o
Эта последовательность проще всего описывается рекурсивно. Пусть S(0) будет последовательность из трех символов "m o o". S(k) получается конкатенацией: копии последовательности S(k-1), затем “m o … o” c k+2 символами ‘o’ и затем еще одна копия последовательности S(k-1). Например:
S(0) = "m o o" S(1) = "m o o m o o o m o o" S(2) = "m o o m o o o m o o m o o o o m o o m o o o m o o"
Очевидно, так можно построить строку любой длины и эта строка используется для игры в “Moo”.
Беси, которая про себя думает, что она умная корова, хочет предсказать, Каким будет символ на позиции N – ‘m’ или ‘o’. Помогите ей!
PROBLEM NAME: moo
Формат входных данных
* Строка 1: Одно целое число N (1 <= N <= 10^9).
Формат выходных данных
* Строка 1: Единственная строка вывода должна содержать один символ, ‘m’ или ‘o’.

Последовательность(2)

Каждый член последовательности десятичных цифр d¹, d², d³..., начиная с четвёртого, равен последней цифре суммы трёх предыдущих. По заданным d¹, d², d³ найти N-й член последовательности.

Ограничения: 1 <= N <= 10¹⁵.

Входные данные
В первой строке находятся цифры d₁, d₂, d₃, разделённые пробелами, во второй - число N.

Выходные данные
Вывести одну цифру - d_N.

Строки Фибоначчи

Строку Фибоначчи F(K) для натуральных чисел K определим так: F(1) = 'A', F(2) = 'B', F(K) = F(K - 1) + F(K - 2) при K > 2, где "+" означает конкатенацию строк. Требуется найти количество вхождений строки S, состоящей из символов A и B, в строку Фибоначчи F(N).

Ограничения: длина S от 1 до 25, 1 <= N <= 45.

Примечание. Длина F(45) равна 1 134 903 170.

Входные данные
В первой строке содержится число N, во второй - строка S.

Выходные данные
Выводится одно число - количество вхождений строки S в строку Фибоначчи F(N).

N-е число Фибоначчи

Последовательность Фибоначчи определяется так: \(f_0 = 0, f_1 = 1, ..., f_n = f_{n-1}+f_{n-2}\).

По данному числу n определите n-е число Фибоначчи fn.

Примеры