| Условие задачи | | Прогресс |
|
Темы:
Система непересекающихся множеств
Древовидные структуры данных
Минимальный каркас
Беси расположена на сети из N (2≤N≤105) вершин помеченных 1…N и 2N порталов помеченных 1…2N. Каждый портал соединяет две различных вершины u и v (u≠v). Множество порталов может соединять некоторую пару вершин.
Каждая вершина v соседняя для четырёх различных порталов. Список порталов вершины v задаётся как pv=[pv,1,pv,2,pv,3,pv,4].
Ваше текущее положение может быть представлено упорядоченной парой (current vertex,current portal); то есть парой (v,pv,i) где 1≤v≤N и 1≤i≤4. Вы можете использовать одну из следующих операций для изменения своего текущего положения:
Изменить текущую вершину перемещением через текущий портал.
Переключить текущий портал. В каждой вершине первые два портала в списке объединены в пару и последние два портала в списке также объединены в пару. Поэтому если Ваше текущее состояние (v,pv,2), то Вы можете переключиться чтобы использовать портал (v,pv,1) и обратно. Аналогично, если Ваше текущее положение (v,pv,3) Вы можете переключиться на портал (v,pv,4) и обратно. никакие другие переключения не разрешены (например, Вы не можете переключиться с портала pv,2 на портал) pv,4).
Всего имеется 4N различных состояний. К несчастью, может не оказаться, что что любое состояние достижимо из любого с помощью последовательности заданных операций. Поэтому, за цену cv (1≤cv≤1000) мунов вы можете сделать перестановку списка порталов соседних вершине v, в любом желаемом Вами порядке. После этого первые два портала в списке объединяются в одну пару, а последние два портала - в другую пару.
Например, если Вы переставить порталы вершины v в порядке [pv,3,pv,1,pv,2,pv,4], Это означает. что если Вы в вершине v,
Если Вы в портале pv,1, Вы можете переключиться на портал pv,3 и обратно
Если Вы в портале pv,2, Вы можете переключиться на портал pv,4 и обратно
Теперь Вы не можете переключаться с портала pv,1 на pv,2, или с портала pv,3 на портал pv,4 и обратно.
Вычислите минимальное количество мунов, требуемых для модификации сети таким образом, чтобы сделать достижимым каждое состояние из каждого состояния. Гарантируется, что тестовые данные сконструированы таким образом, что существует хотя бы один способ такой модификации сети.
Входные данные:
Первая строка содержит N.
Каждая из следующих N строк описывает вершину. Строка v+1 содержит 5 разделённых одиночными пробелами целых чисел cv,pv,1,pv,2,pv,3,pv,4.
Гарантируется, что для каждой v все pv,1,pv,2,pv,3,pv,4 различны, и каждый портал появляется в списках ровно двух вершин.
Выходные данные:
Одна строка содержит минимальное количество мунов требуемых для модификации сети чтобы сделать возможным достижимость каждого состояния из другого состояния.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5
10 1 4 8 9
11 1 2 5 6
12 9 10 2 3
3 4 3 6 7
15 10 8 7 5 |
13 |
Достаточно сделать перестановку списков вершин 1 и 4. Это требует c1+c4=13 мунов. Перестановки такие: p1=[1,9,4,8] и p4=[7,4,6,3]. |
| |
![]()
|
|
Темы:
Динамическое программирование на графах
Древовидные структуры данных
Рассмотрим сеть из N (2≤N≤100) вершин, помеченных 1…N. Каждая вершина обозначена как посылатель, получатель или ни то, ни другое. Количество посылателей S равно количеству получателей (S≥1).
Связи между двумя вершинами в сети могут быть описаны как список направленных ребер каждое в виде i→j, обозначающее, что вершина i может передать информацию вершине j. Интересно, что все эти рёбра удовлетворяют свойству i<j, кроме K которые удовлетворяют свойству i>j (0≤K≤2). Нет циклов (ребер вида i→i).
Описание схемы маршрутизации состоит из множества S направленных путей от посылателей к получателям таких, что никакие два из этих путей не имею общую конечную точку. То есть пути соединяют различных посылателей с различными получателями. Путь от посылателя s к получателю r может быть описан как последовательность вершин
s=v0→v1→v2→?→ve=r
такая что направленные ребра vi→vi+1 существуют для всех 0≤i<e. Одна вершина может появиться более чем один раз в одном и том же пути.
Посчитайте количество различных схем маршрутизации, таких, что каждое направленное ребро проходится ровно один раз. Поскольку ответ может быть очень большим, выводите его по модулю 109+7. Гарантируется, что существует хотя бы одна схема маршрутизации, удовлетворяющая ограничениям.
Каждый ввод содержит T (1≤T≤20) тестов, которые требуется решать независимо. Гарантируется, что сумма N2 всех тестов не превысит 2⋅104.
Входные данные:
Первая строка содержит T, количество тестов.
Первая строка каждого теста содержит целые числа N и K. Заметим, что S не определяется явно во вводе.
Вторая строка каждого теста содержит строку длины N. i-ый символ строки равен S если i-ая вершина посылатель, R - если i-ая вершина - получатель, . - если i-ая вершина - ни то, ни другое. Количества символов R и S равны. Есть хотя бы один символ S.
Каждая из N последующих строк теста содержит битовую строку из N нулей и единиц. j-ый бит в i-ой строке равен 1, если существует направленное ребро от вершины i к вершине j, и 0 в протвном случае. Поскольку петель нет, на главной диагонали все нули. Более того имеется ровно K единиц ниже главной диагонали.
Последовательные тесты разделены пустыми строками для читабельности.
Выходные данные:
Для каждого теста выведите количество схем маршрутизации таких, что каждое ребро проходится ровно один раз, по модулю 109+7. Гарантируется, что существует хотя бы одна валидная схема маршрутизации.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
2
8 0
SS....RR
00100000
00100000
00011000
00000100
00000100
00000011
00000000
00000000
13 0
SSS.RRRSS.RR.
0001000000000
0001000000000
0001000000000
0000111000000
0000000000000
0000000000000
0000000000000
0000000001000
0000000001000
0000000000110
0000000000000
0000000000000
0000000000000 |
4
12 |
Для первого теста ребра таковы 1→3,2→3,3→4,3→5,4→6,5→6,6→7,6→8.
Имеется четыре схемы маршрутизации:
1→3→4→6→7,2→3→5→6→8
1→3→5→6→7,2→3→4→6→8
1→3→4→6→8,2→3→5→6→7
1→3→5→6→8,2→3→4→6→7
Для второго теста 1→4,2→4,3→4,4→5,4→6,4→7,8→10,9→10,10→11,10→12.
Одна из возможных схем маршрутизации:
1→4→5
2→4→7
3→4→6
8→10→12
9→10→11
В общем случае посылатели {1,2,3} могут маршрутизироваться некоторой перестановкой получателей {5,6,7}, и посылатели {8,9} могут маршрутизироваться некоторой перестановкой получателей {11,12} давая ответ 6 ⋅ 2=12.
|
| 2 |
2
5 1
SS.RR
00101
00100
10010
00000
00000
6 2
S....R
001000
000100
010001
000010
001000
000000 |
3
1 |
Для первого теста, ребра 1→3,1→5,2→3,3→1,3→4.
имеется три схемы маршрутизации:
1→3→1→5, 2→3→4
1→3→4, 2→3→1→5
1→5, 2→3→1→3→4
Для второго теста 1→3,2→4,3→2,3→6,4→5,5→3.
Имеется только одна схема мартшрутизации: 1→3→2→4→5→3→6. |
| 3 |
5
3 2
RS.
010
101
100
4 2
.R.S
0100
0010
1000
0100
4 2
.SR.
0000
0011
0100
0010
5 2
.SSRR
01000
10101
01010
00000
00000
6 2
SS..RR
001010
000010
000010
000010
100101
000000 |
2
1
2
6
24 |
|
| |
![]()
|
|
Темы:
Игры и выигрышные стратегии
Простые игры
Древовидные структуры данных
В двусвязном списке, он же LinkedList, каждый элемент может быть связан максимум с двумя другими элементами — с предыдущим элементом (если он есть) и со следующим элементом (если он есть).
Билли и Рикардо проходят стажировку в компании FlexDex в группе поддержки внутреннего анонимного форума с возможностью деанонимизации. Для представления последовательных сообщений в теме необходимо использовать список, где элементами будут являться эти сообщения, и два товарища решили написать свою быструю реализацию двусвязного списка FlexList.
Но у них что-то пошло не так — в их списке новое сообщение может связываться не только с первым или последним сообщением, как должно быть, а с любым из уже существующих сообщений.
Если представить каждое сообщение как вершину графа, а связи между сообщениями как ребра графа, то гарантируется, что этот граф будет неориентированным, связным и ацикличным.
Говорится, что граф является корректным графом, если в этом графе у каждой вершины не более двух вершин, связанных с ней ребром. Изначально же FlexList связи между сообщениями могут выглядеть в виде любого связного ацикличного графа, не обязательно корректного.
Билли и Рикардо не растерялись и решили, что будут вручную исправлять все неясности в ходе работы программ, которые используют их изобретение. Тимлид дал им тестовый пример для проверки кода. Они получили на этом примере граф связей и вручную делают из него корректный граф, ведь связи между сообщениями в корректном двусвязном списке могут представлять собой только корректный граф.
Это выглядит так — сначала Билли проверяет, что граф корректный. Если это не так, то он выбирает и удаляет некоторый лист (вершина, у которой есть ровно одна связь с другими вершинами), и отдает граф Рикардо, затем Рикардо делает то же самое и отдает граф Билли, и так продолжается до тех пор, пока кто-то не получит от товарища корректный граф. Как только один из двух друзей получает такой граф, то тут же показывает его тимлиду, с надеждой на похвалу и повышение в должности.
Каждый хочет получить первым такой граф. Кто первым попадет к тимлиду, если оба товарища удаляют листья оптимально для себя?
Входные данные
В первой строке содержится одно целое число n (1 ≤ n ≤ 300000) — число сообщений в примере тимлида. Следующие n−1 строк задают связи между сообщениями. Каждая из них содержит два целых числа ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi), которые показывают, что сообщения с номерами ai и bi связаны.
Выходные данные
Выведите "Billy" (без кавычек), если первым попадет к тимлиду Билли, иначе выведите "Ricardo" (без кавычек).
Примечание
В первом примере Билли первым ходом может удалить одну из вершин с номерами 2, 4 или 5, так как они являются листьями. Он не будет удалять вершину с номером 4 или 5, так как в таком случае он передаст Рикардо корректный граф и проиграет. Значит, он удалит вершину 2. В свою очередь, Рикардо может удалить вершины 1, 4 или 5, и, в любом случае, Билли получит от него корректный граф.
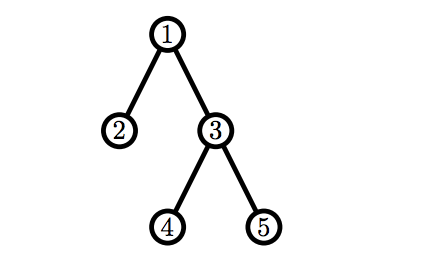
Во втором примере у Билли сразу есть корректный граф.
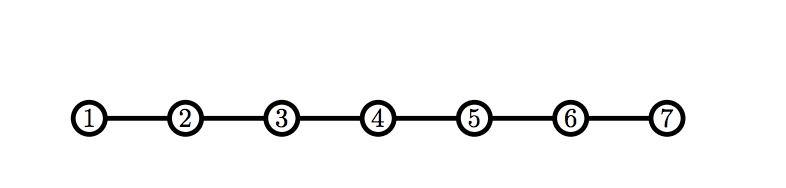
В третьем примере можно показать, что вне зависимости от ходов Билли, Рикардо получит корректный граф первым.
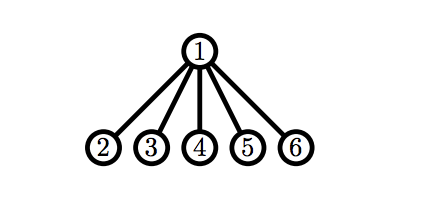
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 2
1 3
3 4
3 5 |
Billy |
| 2 |
7
1 2
2 3
3 4
4 5
5 6
6 7 |
Billy |
| 3 |
6
1 2
1 3
1 4
1 5
1 6 |
Ricardo |
| |
![]()
|