|
Схема игры
Перебор
Разбиения
В тактике футбола одним из основных понятий является схема игры. Она определяет, сколько из десяти полевых игроков будут играть в защите, сколько — в полузащите и сколько — в нападении.
Например, схема игры 5-3-2 означает, что в команде пять защитников, три полузащитника и два нападающих. В соответствии с современными представлениями на схему игры накладываются следующие ограничения: должно быть не менее одного и не более пяти защитников, не менее одного и не более пяти полузащитников и не более трех нападающих. Отметим, что нападающих может в команде и не быть совсем. Будем рассматривать только такие схемы.
Будем считать, что футбольное поле имеет длину 120 метров и ширину 80 метров. Введем на нем прямоугольную декартову систему координат таким образом, как показано на рисунке. Ворота рассматриваемой нами команды находятся слева.
Будем также считать, что игрок в некоторый момент времени находится в линии полузащиты, если он находится на расстоянии не более 20 метров от центральной линии. Соответственно, игрок находится в линии защиты, если он находится не более чем в 40 метрах от «своей» лицевой линии, и в линии нападения, если находится не более чем в 40 метрах от «чужой» лицевой линии.
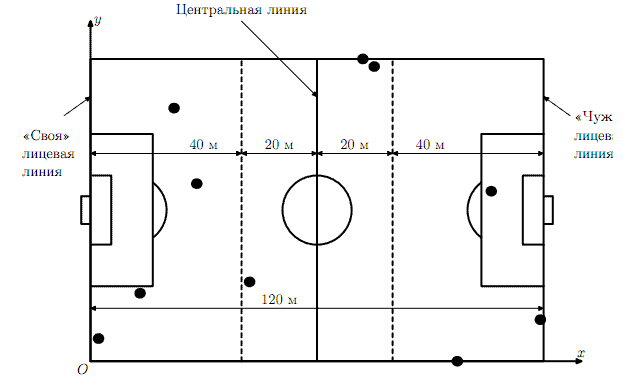
Например, в ситуации, изображенной на рисунке, в линии защиты находятся четыре игрока, в линии полузащиты — три, в линии нападения — также три.
В процессе игры некоторые игроки могут перемещаться из одной линии в другую. В этой задаче будем считать, что возможно перемещение из полузащиты в защиту (и обратно) и из полузащиты в нападение (и обратно). Таким образом, игрок, который в соответствии со схемой игры является защитником, не может оказаться в линии нападения, и наоборот — игрок, который в соответствии со схемой игры является нападающим, не может оказаться в линии защиты. Кроме этого, в соответствии с установкой тренера из каждой линии в каждую могло перейти не более двух игроков.
Ваша задача состоит в том, чтобы написать программу, которая по положениям игроков в некоторый момент времени найдет все возможные схемы игры, при которых в течение игры могло возникнуть такое расположение игроков.
Входные данные
Входной файл содержит десять строк, содержащих по два целых числа xi и yi каждая, — координаты каждого из игроков команды (0 ≤ xi ≤ 120, xi ≠ 40, xi ≠ 80, 0 ≤ yi ≤ 80).
Выходные данные
В первой строке выходного файла выведите k — число схем игры, по которым может играть команда. В последующих k строках в произвольном порядке выведите описание каждой из этих схем. Следуйте формату данных, приведенному в примере.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
97 0
13 18
2 6
119 11
42 21
72 80
75 78
106 45
22 67
28 47 |
9
2-5-3
3-5-2
3-4-3
4-5-1
4-4-2
4-3-3
5-4-1
5-3-2
5-2-3 |
| |
![]()
|
|
Разбиение на невозрастающие слагаемые, лексикографический порядок
Рекурсия
Разбиения
Дано натуральное число N. Рассмотрим его разбиение на натуральные слагаемые. Два разбиения, отличающихся только порядком слагаемых, будем считать за одно, поэтому можно считать, что слагаемые в разбиении упорядочены по невозрастанию.
Входные данные
Задано единственное число N. (N ≤ 40)
Выходные данные
Необходимо вывести все разбиения числа N на натуральные слагаемые в лексикографическом порядке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 |
1 1 1 1 1
2 1 1 1
2 2 1
3 1 1
3 2
4 1
5 |
| |
![]()
|