| | | |
|
Кинотеатр
Динамическое программирование: последовательности
X мальчиков и Y девочек пошли в кинотеатр и купили билеты на подряд идущие места в одном ряду. Напишите программу, которая выдаст, как нужно сесть мальчикам и девочкам, чтобы рядом с каждым мальчиком сидела хотя бы одна девочка, а рядом с каждой девочкой — хотя бы один мальчик.
Входные данные
Вводятся два числа — X и Y (оба числа натуральные, не превосходящие 100).
Выходные данные
Выведите какую-нибудь строку, в которой будет ровно X символов B (обозначающих мальчиков) и Y символов G (обозначающих девочек), удовлетворяющую условию задачи. Пробелы между символами выводить не нужно. Если рассадить мальчиков и девочек согласно условию задачи невозможно, выведите строку NO SOLUTION.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 5 |
BGBGBGBGBG |
| 2 |
5 3 |
BGBGBBGB |
| 3 |
100 1 |
NO SOLUTION |
| |
![]()
|
|
НВП на отрезке
Динамическое программирование: последовательности
Нам дана числовая последовательность a1, ..., an . Напишите программу, отвечающую на запросы вида "найти длину наибольшей строго возрастающей подпоследовательности, все элементы которой находятся на отрезке с li-ого по ri-ый элемент".
Подпоследовательностью последовательности a1 , ..., an называется последовательность, которую можно получить путем удаления нескольких элементов ai (относительный порядок оставшихся элементов менять запрещается). Так, например, последовательность (2, 4) является подпоследовательностью последовательности (1, 2, 3, 4, 5) (можно удалить элементы 1, 3 и 5 ), а последовательность (5, 1) - нет.
Входные данные
В первой строке записано целое число n (1 <= n <= 3000 ) - число элементов в последовательности. Во второй строке записано n чисел, разделенных пробелами - элементы последовательности. Все элементы не превосходят по модулю 10 9. В третьей строке записано одно целое число q (1 <= q <= 10 5) - количество запросов. В следующих q строках описаны запросы. Описание i -ого запроса - два числа li и rj (1 <= l i <= r i <= n) , записанные через пробел.
Выходные данные
Выведите q чисел - ответы на запросы. Числа следует выводить по одному на строке в том же порядке, в котором запросы описаны во вводе.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
3 3 -5 7 4 9
6
1 4
1 2
2 3
1 5
3 5
2 5 |
2
1
1
2
2
2 |
| |
![]()
|
|
Little Difference
Динамическое программирование: последовательности
Конструктив
Little Lidia likes playing with numbers. Today she has a positive integer n, and she wants to decompose it to the product of positive integers.
Because Lidia is little, she likes to play with numbers with little difference. So, all numbers in decomposition should differ by at most one. And of course, the product of all numbers in the decomposition must be equal to n. She considers two decompositions the same if and only if they have the same number of integers and there is a permutation that transforms the first one to the second one.
Write a program that finds all decompositions, which little Lidia can play with today.
Input
The only line of the input contains a single integer n (1 ≤ n ≤ 1018).
Output
In first line output the number of decompositions of n, or −1 if this number is infinite. If number of decompositions is finite, print all of them one per line. In each line first print number ki of elements in decomposition. Then print ki integers in this decomposition in any order. Don’t forget that decompositions which are different only in order of elements are considered the same.
| Input |
Output |
| 12 |
3
1 12
3 2 3 2
2 4 3 |
| 1 |
-1 |
In the second example 1 can be represented as product of any number of ones.
| |
![]()
|
|
Упорядочите шарики
Динамическое программирование
Динамическое программирование: последовательности
При игре в новую игру (некоторый гибрид боулинга и бильярда) используется N шариков, пронумерованных числами от 1 до N. В начале игры эти шарики должны быть выложены в линию в порядке своих номеров. В процессе игры их порядок может меняться.
Для того, чтобы упорядочить шарики перед началом следующей партии, используется следующее устройство. Это устройство состоит из головки, которая, перемещаясь над шариками, может «засасывать» и «выплевывать» шарики. Чтобы получить большее представление об этом устройстве, представьте себе пылесос, который может засасывать шарики, перемешаться в нужное место, и там, включаясь на продув в обратном направлении, шарики «выплевывать».
При засасывании шарика все шарики, которые находились правее засасываемого, сдвигаются влево. «Выплюнуть» шарик можно между любыми двумя шариками (а также перед первым шариком или после последнего), тогда выплевываемый шарик вставляется между этими шариками, и все шарики, которые находятся правее вставляемого, сдвигаются вправо.
В устройство может быть одновременно засосано больше одного шарика, при этом при выплевывании шарика первым выплевывается последний засосанный шарик, затем - предпоследний и т.д. (т.е. устройство работает по принципу стека). Шарики выплевываются по одному, т.е. можно выплюнуть только один шарик, остальные оставив внутри устройства (при этом дальше можно как продолжать «выплевывать» шарики в том же или в другом месте, так и засасывать новые шарики).
Наиболее энергоемкой из описанных операций является операция засасывания шарика, поэтому хочется минимизировать количество именно таких операций.
Напишите программу, которая по данному начальному расположению шариков определит минимальное количество операций засасывания, которое нужно, чтобы расположить шарики в порядке их номеров.
Входные данные
Во входном файле задано сначала число N — количество шариков (1<= N <= 1000). Далее идет N чисел, задающих номера шариков в порядке слева направо в их текущем расположении (каждое число — от 1 до N, и каждое из чисел встречается в последовательности ровно один раз).
Выходные данные
В выходной файл выведите одно число — минимальное количество операций засасывания шарика, которое потребуется, чтобы расположить шарики в порядке их номеров.
Комментарии к примерам тестов
1.Можно засосать, например, шарик номер 2 и выплюнуть его между 1-м и 3-м шариком.
2. Можно действовать, например, так. Сначала засосем шарик номер 1, затем – шарик номер 2. Затем переместимся в начало и перед 4-м шариком выплюнем шарик (это будет шарик номер 2). Дальше засосем шарик номер 3, и выплюнем его между шариками 2 и 4. Дальше переместимся в начало и там выплюнем шарик номер 1. Впрочем, это не единственный возможный вариант упорядочения шариков в этом примере.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
2 1 3 |
1 |
| 2 |
4
4 3 2 1 |
3 |
| |
![]()
|
|
Наибольшая возрастающая подпоследовательность за O(n*log(n))
Динамическое программирование
Динамическое программирование: последовательности
Динамическое программирование: последовательности
Числовая последовательность задана рекуррентной формулой: ai+1=(k * ai + b) mod m. Найдите длину её наибольшей возрастающей подпоследовательности.
mod - операция вычисления остатка от деления
Входные данные
Программа получает на вход пять целых чисел: длину последовательности n (1≤n≤105), начальный элемент последовательности a1, параметры k, b, m для вычисления последующих членов последовательности (1≤m≤104, 0≤k<m, 0≤b<m, 0≤a1<m).
Выходные данные
Требуется вывести длину наибольшей возрастающей подпоследовательности данной последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 41 2 1 100
|
3
|
| |
![]()
|
|
Наибольшая возрастающая подпоследовательность за O(n*log(n))
Динамическое программирование
Динамическое программирование: последовательности
Динамическое программирование: последовательности
Числовая последовательность задана рекуррентной формулой: ai+1=(k * ai + b) mod m. Найдите длину её наибольшей возрастающей подпоследовательности.
mod - операция вычисления остатка от деления
Входные данные
Программа получает на вход пять целых чисел: длину последовательности n (1≤n≤105), начальный элемент последовательности a1, параметры k, b, m для вычисления последующих членов последовательности (1≤m≤104, 0≤k<m, 0≤b<m, 0≤a1<m).
Выходные данные
Требуется вывести длину наибольшей возрастающей подпоследовательности данной последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 41 2 1 100
|
3
|
| |
![]()
|
|
Кристаллы максимуса
Динамическое программирование
Динамическое программирование: последовательности
Задача о рюкзаке
 Максимус очень любит коллекционировать кристаллы. Среди всех кристаллов у него есть один самый любимый с магической силой равной Максимус очень любит коллекционировать кристаллы. Среди всех кристаллов у него есть один самый любимый с магической силой равной n. Также у него есть коллекция совершенных кристаллов. Совершенный кристалл - это кристалл, магическая сила которого равна квадрату натурального числа.
У Максимуса выдался свободный вечер, и он задумался: сколько нужно ему совершенных кристаллов, чтобы сумма их магических сил равнялась бы магической силе его любимого кристалла?
Квадратом натурального числа является число, которое получается умножением натурального числа на себя. Например, 1, 4 и 9 - это квадраты натуральных чисел, а 2, 3 и 5 - нет.
Ваша задача - помочь Максимусу найти минимальное количество совершенных кристаллов, сумма магических сил которых равна n.
Входные данные
Программа получает на вход натуральное число n (n < 104).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
12
|
3
|
12 = 4 + 4 + 4 |
| 2 |
13 |
2 |
13 = 4 + 9 |
| |
![]()
|
|
Магическая подпоследовательность Айвена
Динамическое программирование
Динамическое программирование: последовательности
Юный волшебник Айвен считает последовательность символов магической, если она является палиндромом (то есть читается одинаково как слева направо, так и справа налево). Айвену попалась в руки последовательность символов s. Он хочет удалить из нее любое (возможно нулевое) количество символов, чтобы получить из нее самую длинную магическую подпоследовательность.
Определите длину самой длинной магической подпоследовательности, которую сможет получить Айвен.
Входные данные
Программа получает на вход последовательность символов s (1<= |s| <= 1000), состоящую из строчных английских букв.
Выходные данные
Выведите одно число - длину самой длинной магической подпоследовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
bbbab
|
4
|
| |
![]()
|
|
Фишки-палочки
Динамическое программирование
Динамическое программирование: последовательности
Алиса и Громозека играют в фишки-палочки. У каждого из них есть набор фишек, на каждой фишке записано одно целое число. Каждый из них выкладывает свои фишки вдоль двух параллельных горизонтальных линий. Следующим шагом Алиса соединяет палочкой две фишки, расположенные на разных горизонтальных линиях, то есть соединяет одну свою фишку с одной из фишек Громозеки по следующим правилам:
- числа, на фишке Алисы и на фишке Громозеки равны;
- соединяющая палочка не должна пересекать другие палочки;
- две палочки не могут указывать на одну и ту же фишку.
Далее, Громозека считает сколько палочек выложила Алиса. После этого, Алиса убирает свои палочки и фишки соединяет Громозека по тем же правилам. Выигрывает тот, кто выложит по данным правилам больше всего палочек.
Вас, как наблюдателя за этой игрой, просят определить максимальное количество палочек, которые можно выложить по указанным правилам.
Входные данные
Первая строка входных данных содержит число n - количество фишек Алисы. Вторая строка содержит n чисел nums1i - числа на фишках Алисы, в том порядке, в котором она их выложила. Третья строка содержит число m - количество фишек Громозеки. Четвертая строка содержит m чисел nums2j - числа на фишках Громозека, в том порядке, в котором он их выложил.
Ограничения
1 <= n, m <= 5001 <= nums1[i], nums2[j] <= 2000
Выходные данные
Выведите одно число - максимальное количество палочек, которые можно выложить по указанным в условии задачи правилам игры.
Примечание
Рисунок к первому тестовому примеру
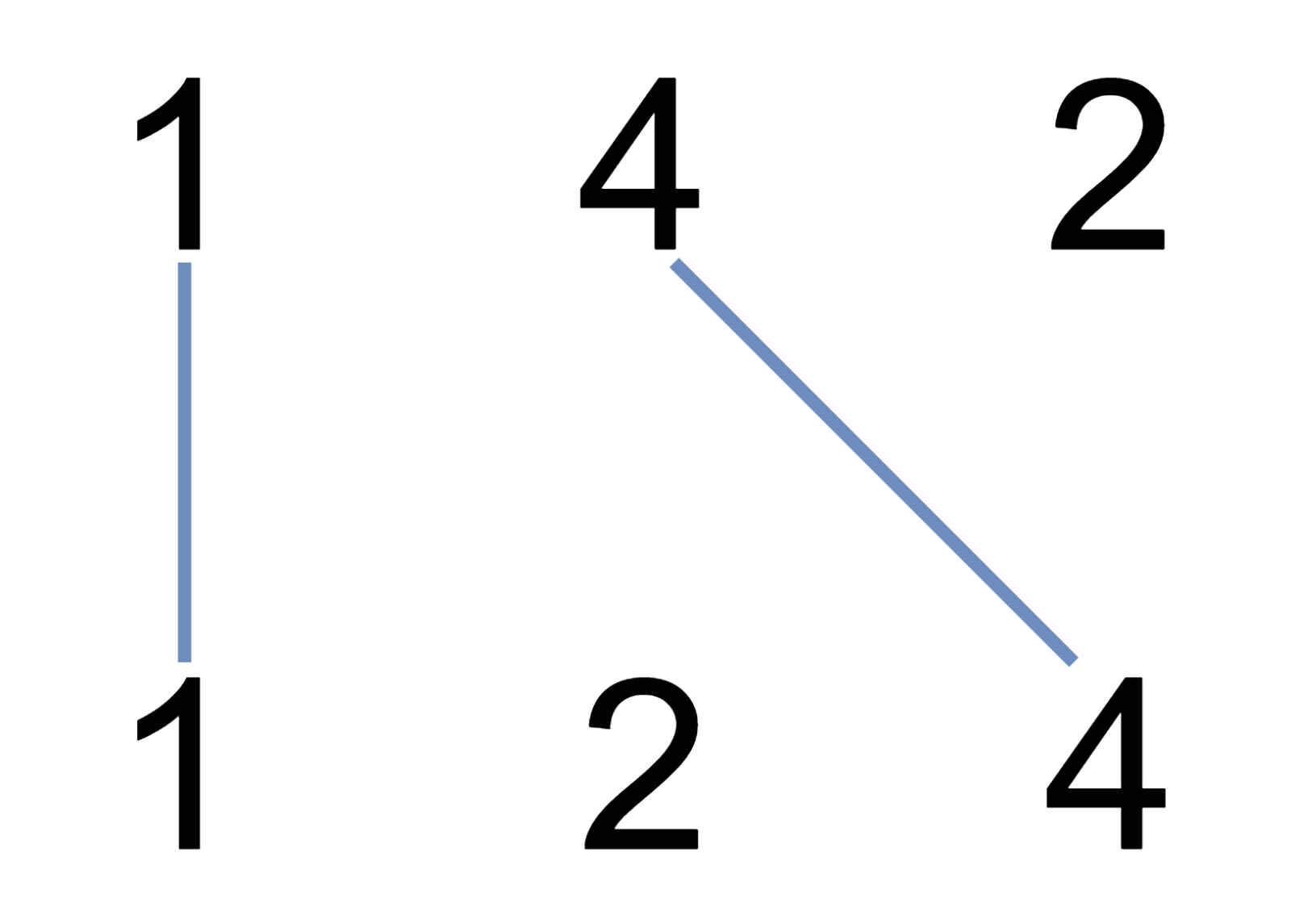
| |
![]()
|
|
Головоломка
Динамическое программирование: последовательности
Пете на день рождения подарили новую головоломку. Головоломка представляет собой цилиндр, состоящий из n круглых слоев, нанизанных на одну вертикальную ось. Каждый слой можно вращать независимо от других. Каждый слой разбит на n квадратиков, каждый из которых может быть либо черным, либо белым. В устойчивом состоянии квадратики соседних слоев находятся в точности друг под другом.
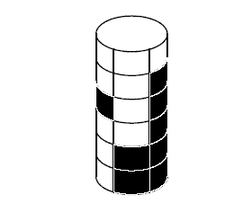
Для задания конфигурации головоломки удобно рассмотреть ее развертку - "разрезать" поверхность цилиндра вдоль вертикальной линии, проходящей по границам квадратиков, и обозначить черные клетки символом "1", а белые - символом "0". Пусть, например, одна из возможных разверток головоломки, приведенной на рисунке, следующая (на рисунке видно только первые три столбца этой развертки):
000110 001110 101000 001000 011111 011110
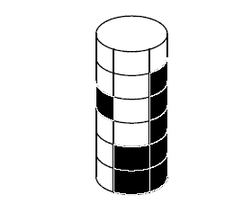
Задача решающего головоломку состоит в том, чтобы, поворачивая слои, добиться того, чтобы все вертикальные столбцы были различны. Например, головоломка приведенная выше, не решена, поскольку два из ее столбцов (четвертый и пятый на приведенной развертке) одинаковы. Если же повернуть нижний слой влево на один квадратик, развертка головоломки примет следующий вид:
000110 001110 101000 001000 011111 111100
Теперь все столбцы различны и, следовательно, головоломка решена.
Для того, чтобы решать головоломку было интереснее, на ее раскраску наложено дополнительное условие: нельзя повернуть один из слоев головоломки меньше, чем на полный оборот таким образом, что внешний вид головоломки останется тем же. Так, например, для n = 6 слой с раскраской "010101" не разрешается, поскольку при его повороте на 2 квадратика внешний вид головоломки не меняется.
По заданной развертке головоломки выясните, можно ли ее решить, и если да, то приведите пример развертки решенной головоломки.
Входные данные
В первой строке вводится число n - количество слоев в головоломке и количество квадратиков в одном слое (1 <= n <= 200). Следующие n
строк содержат по n символов, каждый из которых равен 0 или 1 - развертку головоломки.
Выходные данные
Если решить головоломку можно, в первой строке выведите слово "Yes". В этом случае следующие n строк должны содержать произвольную развертку решенной головоломки.
Если решить головоломку нельзя, выведите в первой и единственной строке выходных данных слово "No".
| |
![]()
|
|
Возрастающая подпоследовательность
Динамическое программирование: последовательности
Даны N целых чисел X1, X2, ..., XN. Требуется вычеркнуть из них минимальное количество чисел так, чтобы оставшиеся шли в порядке возрастания.
Входные данные
В первой строке находится число N. В следующей строке - N чисел через пробел. 1 <= N <= 10 000, 1 <= Xi <= 60 000.
Выходные данные
В первой строке выводится количество невычеркнутых чисел, во второй - сами невычеркнутые числа через пробел в исходном порядке. Если вариантов несколько, вывести любой.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 3 5 2 4
|
3
1 3 4
|
| |
![]()
|
|
Анаграммер
Динамическое программирование: последовательности
Анаграммер — специальное устройство для получения из слова его анаграмм (то есть слов, записанных теми же буквами, но в другом порядке). Это устройство умеет выполнять 2 операции:
- Взять очередную букву исходного слова и поместить ее в стек.
- Взять букву из стека и добавить ее в конец выходного слова.
Стек — это хранилище данных, которое работает по принципу "первый пришел — последний ушел". Стек можно представить себе в виде пирамидки. Когда мы добавляем букву в стек, это соответствует тому, что на стержень пирамидки сверху мы надеваем кольцо, на котором написана соответствующая буква. Когда берем букву из стека, то это соответствует тому, что мы снимаем со стержня верхнее кольцо, и смотрим, какая буква на нем написана.
Например, слово TROT в слово TORT может быть преобразовано анаграммером двумя различными последовательностями операций: 11112222 или 12112212.
Напишите программу, которая по двум заданным словам вычисляет количество различных последовательностей операций анаграммера, которые преобразуют первое из этих слов во второе, а также находит сами эти последовательности.
Входные данные
Первая строка входного файла содержит исходное слово, а вторая — слово, которое необходимо получить. Слова состоят только из заглавных латинских букв и имеют длину не более 50 символов. Оба слова имеют одинаковую длину. В этих строках не содержится пробелов.
Выходные данные
В первой строке выходного файла должно содержаться количество последовательностей операций анаграммера, с помощью которых можно преобразовать первое слово во второе.
Если это количество не превышает 1000, то в последующих строках должны содержаться сами последовательности. Каждая последовательность должна быть выведена на отдельной строке, и состоять из цифр 1 и 2 (указывающих порядок выполнения операций), выведенных без пробелов.
| |
![]()
|