| | | |
|
Определите порядок действий
Разбор выражений
Ученику второго класса рассказали правила, как нужно выполнять арифметические действия, чтобы вычислить значение арифметического выражения, состоящего из чисел, скобок и знаков арифметических операций + (сложение) и * (умножение). После этого ему дали упражнения — несколько задач, в которых требуется расставить порядок выполнения действий. Помогите ему.
Правила вычисления выражения, рассказанные ученику, звучат так. Если в выражении вообще нет скобок, то сначала выполняются все операции умножения слева направо, а затем — операции сложения также слева направо. Если же в выражении есть скобки, то находится самая левая пара скобок (открывающая и закрывающая), содержащая внутри себя бесскобочное выражение, которое может быть вычислено по вышеописанным правилам. Дальше это выражение (вместе со скобками) мысленно удаляется из выражения и заменяется числом – результатом. Если в выражении остались скобки, то процедура повторяется.
Напишите программу, которая для корректного выражения будет определять порядок выполнения арифметических действий. Поскольку сами числа в этой задаче нам будут не существенны, мы заменим их на знаки #.
Входные данные
Во входном файле записана одна строка, состоящая из символов #, +, *, (, ). Длина строки не превышает 250 символов. Строка соответствует правильному арифметическому выражению.
Выходные данные
В выходной файл нужно вывести ту же строку, заменив знаки операций + и * в ней натуральными числами, задающими порядок выполнения действий в соответствии с описанными правилами.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
#+#*# |
#2#1# |
| 2 |
#+#+(#+#) |
#2#3(#1#) |
| 3 |
#+(#+#*#)*#+# |
#4(#2#1#)3#5# |
| 4 |
#+#+#+#+#+#+#+#+#+#+# |
#1#2#3#4#5#6#7#8#9#10# |
| 5 |
#+#+(#+(#+#))+(#+#) |
#4#5(#2(#1#))6(#3#) |
| |
![]()
|
|
Дробь в LATEX-е
Разбор выражений
Разбор выражений
Издательская система LATEX предназначена для верстки сложных научно-технических текстов с большим количеством формул. Исходный файл для системы LATEX пишется на языке TEX и представляет собой текст документа, в который включены специальные символы и команды. Специальные символы и команды описывают размещение текста, в частности в математических формулах. Команда представляет собой последовательность латинских букв (регистр важен), перед которой стоит символ "\". Так, команда \frac предназначена для описания дроби, в которой числитель расположен над знаменателем. Рассмотрим простейшую структуру команды \frac.
Команда \frac имеет два параметра — числитель и знаменатель. Перед самой командой не обязательно ставить пробел. Следом за ключевым словом frac записываются числитель и знаменатель. Если числитель и знаменатель имеют длину более одного символа, они заключаются в фигурные скобки. Если числитель или знаменатель записываются одной буквой или цифрой, их можно не брать в фигурные скобки. Если числитель записывается одним символом, то он отделяется от \frac хотя бы одним пробелом. Если знаменатель записывается одним символом, то он не отделяется пробелом от числителя. Произвольное ненулевое количество пробелов считается синтаксически эквивалентным одному пробелу. Нельзя разделять пробелами на части ключевое слово \frac.
Дадим также формальное определение выражения для нашей задачи:
<выражение> ::= <элемент> | <элемент><выражение>
<элемент> ::= <дробь> | "{" <выражение> "}" | <другой математический элемент>
<дробь> ::= "\frac" <тело дроби>
<тело дроби> ::= <числитель><знаменатель>
<числитель> ::= <пробелы><непробельный символ> | [<пробелы>] "{" <выражение> "}"
<знаменатель> ::= <непробельный символ> | [<пробелы>] "{" <выражение> "}"
<другой математический элемент> ::= произвольная последовательность печатных символов, не содержащая фигурных скобок и подстроки "\frac"
<пробелы> ::= " " | " " <пробелы>
<непробельный символ> ::= произвольный печатный символ, за исключением " ", "", "{" и "}"
Здесь вертикальная черта | означает "или", заключенная в квадратные скобки часть может отсутствовать, а символы, записанные в кавычках обозначают самих себя. Печатный символ - любой символ с ASCII кодом от 32 (пробел) до 127. Например, выражение
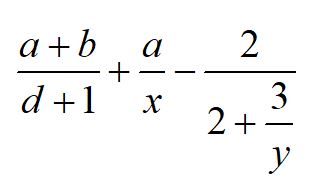
записывается на языке TEX как
\frac{a+b}{d+1}+\frac ax -\frac 2 {2+\frac{3}{y}}
Чтобы в печатаемом документе вывести формулу, необходимо вычислить ее высоту для используемого при печати шрифта. Шрифт определяет размеры S
- высоту отдельного символа и D
- высоту горизонтальной дробной черты. Значения S
и D
задаются целыми числами. Ваша задача - для заданного выражения на языке TEX вычислить высоту формулы.
Отметим, что если две дроби принадлежат одному выражению, то их дробные черты записываются на одном уровне, а если нет (например, относятся к числителям или знаменателям различных дробей), это свойство может и не выполняться. Чтобы проиллюстрировать применение этого правила, приведем два примера:
\frac{a+b}{\frac cd}+\frac{\frac ef}{g+h}
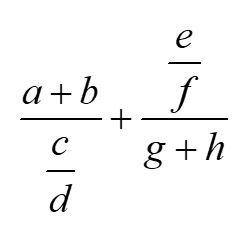
\frac{a+b+c}{\frac{\frac de}{g+h}}+\frac{i+j+k}{\frac{l+m}{\frac no}}
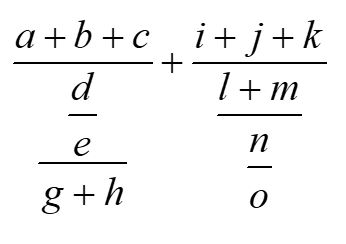
Входные данные
В первой строке вводятся целые положительные числа S и D (1 <= S, D <= 10000). Следующая строка содержит описание формулы на TEX-е, длина строки не более 200 символов. Гарантируется, что формула синтаксически корректна, то есть фигурные скобки образуют правильную скобочную последовательность и строка содержит только печатные символы. Все символы "", встречающиеся в строке относятся к некоторой командной последовательности (не обязательно \frac), можете считать, что все прочие командные последовательности задают символы, высота которых равна S. Числитель и знаменатель каждой дроби содержат хотя бы по одному символу, вся формула содержит хотя бы один символ.
Выходные данные
Выведите единственное число - высоту формулы.
| |
![]()
|
|
Дробь в LATEX-е
Разбор выражений
Разбор выражений
Издательская система LATEX предназначена для верстки сложных научно-технических текстов с большим количеством формул. Исходный файл для системы LATEX пишется на языке TEX и представляет собой текст документа, в который включены специальные символы и команды. Специальные символы и команды описывают размещение текста, в частности в математических формулах. Команда представляет собой последовательность латинских букв (регистр важен), перед которой стоит символ "\". Так, команда \frac предназначена для описания дроби, в которой числитель расположен над знаменателем. Рассмотрим простейшую структуру команды \frac.
Команда \frac имеет два параметра — числитель и знаменатель. Перед самой командой не обязательно ставить пробел. Следом за ключевым словом frac записываются числитель и знаменатель. Если числитель и знаменатель имеют длину более одного символа, они заключаются в фигурные скобки. Если числитель или знаменатель записываются одной буквой или цифрой, их можно не брать в фигурные скобки. Если числитель записывается одним символом, то он отделяется от \frac хотя бы одним пробелом. Если знаменатель записывается одним символом, то он не отделяется пробелом от числителя. Произвольное ненулевое количество пробелов считается синтаксически эквивалентным одному пробелу. Нельзя разделять пробелами на части ключевое слово \frac.
Дадим также формальное определение выражения для нашей задачи:
<выражение> ::= <элемент> | <элемент><выражение>
<элемент> ::= <дробь> | "{" <выражение> "}" | <другой математический элемент>
<дробь> ::= "\frac" <тело дроби>
<тело дроби> ::= <числитель><знаменатель>
<числитель> ::= <пробелы><непробельный символ> | [<пробелы>] "{" <выражение> "}"
<знаменатель> ::= <непробельный символ> | [<пробелы>] "{" <выражение> "}"
<другой математический элемент> ::= произвольная последовательность печатных символов, не содержащая фигурных скобок и подстроки "\frac"
<пробелы> ::= " " | " " <пробелы>
<непробельный символ> ::= произвольный печатный символ, за исключением " ", "", "{" и "}"
Здесь вертикальная черта | означает "или", заключенная в квадратные скобки часть может отсутствовать, а символы, записанные в кавычках обозначают самих себя. Печатный символ - любой символ с ASCII кодом от 32 (пробел) до 127. Например, выражение
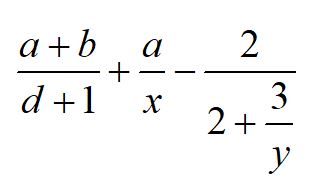
записывается на языке TEX как
\frac{a+b}{d+1}+\frac ax -\frac 2 {2+\frac{3}{y}}
Чтобы в печатаемом документе вывести формулу, необходимо вычислить ее высоту для используемого при печати шрифта. Шрифт определяет размеры S
- высоту отдельного символа и D
- высоту горизонтальной дробной черты. Значения S
и D
задаются целыми числами. Ваша задача - для заданного выражения на языке TEX вычислить высоту формулы.
Отметим, что если две дроби принадлежат одному выражению, то их дробные черты записываются на одном уровне, а если нет (например, относятся к числителям или знаменателям различных дробей), это свойство может и не выполняться. Чтобы проиллюстрировать применение этого правила, приведем два примера:
\frac{a+b}{\frac cd}+\frac{\frac ef}{g+h}
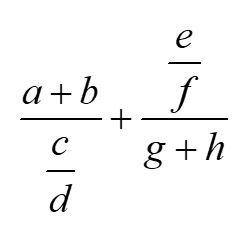
\frac{a+b+c}{\frac{\frac de}{g+h}}+\frac{i+j+k}{\frac{l+m}{\frac no}}
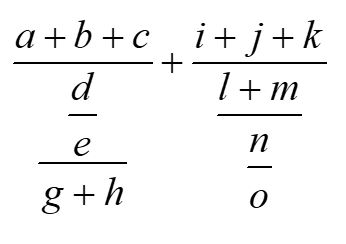
Входные данные
В первой строке вводятся целые положительные числа S и D (1 <= S, D <= 10000). Следующая строка содержит описание формулы на TEX-е, длина строки не более 200 символов. Гарантируется, что формула синтаксически корректна, то есть фигурные скобки образуют правильную скобочную последовательность и строка содержит только печатные символы. Все символы "", встречающиеся в строке относятся к некоторой командной последовательности (не обязательно \frac), можете считать, что все прочие командные последовательности задают символы, высота которых равна S. Числитель и знаменатель каждой дроби содержат хотя бы по одному символу, вся формула содержит хотя бы один символ.
Выходные данные
Выведите единственное число - высоту формулы.
| |
![]()
|
|
Химические реакции
Разбор выражений
Билл преподаёт химию в школе, он подготовил несколько тестов для учеников. Каждый тест состоит из химической формулы и нескольких возможных результатов реакции. Среди этих результатов ученики должны выбрать правильный. Билл хочет убедиться в том, что, вводя свои тесты в компьютер, он не допустил опечаток, благодаря которым ученики могли бы отбросить неверные ответы, просто подсчитав число химических элементов в левой и правой частях уравнения (в правильном уравнении химической реакции должно соблюдаться равенство).
Ваша задача - написать программу, которая поможет Биллу. Программа должна прочитать описание теста, состоящее из заданной левой части уравнения и нескольких возможных правых частей, и определить, равно ли количество химических элементов в каждой предложенной правой части уравнения количеству химических элементов в заданной левой части.
Билл формализовал задачу. И левая, и правая части уравнения представлены строкой символов без пробелов, состоящей из одной или более химических последовательностей, разделённых знаком плюс. Каждая последовательность имеет необязательный предшествующий целый множитель, относящийся ко всей последовательности, и несколько элементов. Каждый элемент может сопровождаться необязательным целым множителем, относящимся к нему. Элемент в этом уравнении может быть или отдельным химическим элементом, или целой последовательностью в круглых скобках. Каждый отдельный химический элемент представлен или одной прописной буквой, или прописной буквой, сопровождаемой строчной.
Ещё более формально, используя нотацию, аналогичную форме Бэкуса-Наура, можно написать:
- <формула> ::= [<число>] <последовательность> {"+" [<число>] <последовательность>}
- <последовательность> ::= <элемент> [<число>] {<элемент> [<число>]}
- <элемент> ::= <химический элемент> | "(" <последовательность> ")"
- <химический элемент> ::= <прописная буква> [<строчная буква>]
- <прописная буква> ::= "A".."Z"
- <строчная буква> ::= "a".."z"
- <число> ::= "1".."9" {"0".."9"}
Будем говорить, что каждый отдельный химический элемент встречается в формуле всего X раз, если X - сумма всех различных вхождений этого химического элемента, умноженных на все числа, относящиеся к ним. Например, в формуле C2H5OH+3O2+3(SiO2)
- C встречается всего 2 раза;
- H встречается всего 6 раз (5 + 1);
- O встречается всего 13 раз; (1 + 3 * 2 + 3 * 2);
- Si встречается всего 3 раза.
Все множители в формулах - целые числа не меньше 2, если заданы явно, или равны 1 - по умолчанию.
Входные данные
В первой строке находится формула - левая часть уравнения, во второй - одно число N - количество рассматриваемых правых частей, в каждой из следующих N строк - одна формула - предлагаемая правая часть уравнения.
Ограничения: 1 <= N <= 10, длина формулы не превосходит 100 символов, каждый отдельный химический элемент встречается всего не более 10 000 раз в каждой формуле.
Выходные данные
Для каждой из N заданных правых частей выведите одну строку вида
<формула левой части>==<формула правой части>
если общее количество вхождений каждого отдельного химического элемента в левую часть равно общему числу вхождений этого химического элемента в правую часть. В противном случае выведите:
<формула левой части>!=<формула правой части>
Здесь <формула левой части> должна быть замещена посимвольной копией формулы левой части, как она дана в первой строке входного файла, а <формула правой части> - замещена точной копией формулы правой части, как она дана во входном файле. В строках не должно быть пробелов.
| |
![]()
|
|
Добрый иероглиф
Разбор выражений
Когда археологи проводили раскопки в древних городах Майя, они обнаружили множество непонятных иероглифов. Пример иероглифа показан справа, он обозначает имя Кьак-у-пакал, это имя военного и религиозного лидера в древнем городе Майя Чичен-Итца (см. А.В.Восс, Г. Дж.Кремер Кьак-у-пакал, Хун-пик-токь и Коком). Этот иероглиф можно увидеть во многих местах древнего города.
Вообще говоря, иероглифы Майя не являются иероглифами в прямом смысле этого слова, а, скорее, являются композицией отдельных глифов. Все известные глифы занумерованы целыми числами от 1 до 9999. Учеными был разработан специальный язык, с помощью которого можно представлять иероглиф в виде обычного текста. Например, иероглиф Кьак-у-пакал кодируется как “((669:604).(586:(27:(534.534))))”.
Приведем формальную грамматику этого языка:
<block> ::= <glyph id>|'('<block>'.'<horizontal group>')'|'('<block>':'<vertical group>')'
<horizontal group> ::= <block>['.'<horizontal group>]
<vertical group> ::= <block>[':'<vertical group>]
Код иероглифа описывает процесс его составления. Глифы комбинируются горизонтально и вертикально (с помощью ':' и '.') в блоки, которые, в свою очередь, комбинируются во все большие и большие блоки, до тех пор, пока не будет достигнута нужная конфигурация.
Как обычно, в процессе реализации забыли о важной части — обратном восстановлении обычного текста в иероглиф. Это предстоит сделать вам.
Входные данные
Единственная строка входного файла содержит строку, описывающую иероглиф Майя в виде обычного текста. Длина строки не превышает 255 символов. Строка не содержит пробелов.
Выходные данные
Выведите текст, составленный из символов '+', '-', '|', ' ' (ASCII коды 43, 45, 124, 32), '0'..'9' и переводов строки. Все блоки одной группы должны иметь одинаковый размер. Номер глифа (glyph id) с одним пробелом перед ним, должен быть помещен в левый верхний угол блока. Вывод должен быть как можно короче. Гарантируется, что для всех тестов существует изображение, содержащее максимум 100 000 байт.
| |
![]()
|
|
D. Арифметическое выражение
дп
Разбор выражений
*2600
Определим арифметическое выражение (АВ) следующим образом. - Каждое неотрицательное целое число является АВ. Целые числа могут иметь лидирующие нули (например, 0000 и 0010 считаются допустимыми целыми числами).
- Если X и Y являются АВ, то «(X) + (Y)», «(X) - (Y)», «(X) * (Y)», и «(X) / (Y)» (без кавычек) тоже являются АВ.
- Если X является АВ, то « - (X)» и « + (X)» (без кавычек) тоже являются АВ.
Дана строка, состоящая из цифр («0» - «9») и символов «-», «+», «*», и «/». Ваша задача — посчитать количество арифметических выражений, таких, что после удаления из него всех скобок (символов «(» и «)»), это выражение становится эквивалентным данной строке. Так как ответ может быть очень большим, выведите его по модулю 1000003 (106 + 3). Выходные данные Выведите одно целое число — количество различных арифметических выражений, которые после удаления из них скобок становятся посимвольно равными данной строке, по модулю 1000003 (106 + 3). Примечание В первом примере возможны два арифметических выражения: ((1) + (2)) * (3)
(1) + ((2) * (3)) Во втором примере возможны три арифметических выражения: (03) + (( - (30)) + (40))
(03) + ( - ((30) + (40)))
((03) + ( - (30))) + (40) | |
![]()
|
|
B. Поймай переполнение!
Разбор выражений
реализация
Структуры данных
*1600
Задана функция \(f\), написанная на довольно примитивном языке. Функция принимает целое значение, которое сразу записывается в переменную \(x\). \(x\) — это целочисленная переменная, которая может принимать значения от \(0\) до \(2^{32}-1\). Функция содержит три типа команд: - for \(n\) — цикл for;
- end — каждая команда между «for \(n\)» и соответствующим «end» выполняется \(n\) раз;
- add — прибавляет 1 к \(x\).
После выполнения команд возвращается значение \(x\). Каждый «for \(n\)» имеет парный «end», поэтому гарантируется, что функция корректна. За «for \(n\)» может сразу следовать «end». «add» может быть расположен вне циклов for. Заметили, что команда «add» может переполнить значение \(x\)! Это значит, что значение \(x\) становится больше \(2^{32}-1\) после некоторой команды «add». Теперь запускается \(f(0)\), а ваша задача — узнать, корректно ли полученное значение \(x\) или переполнение сделает его некорректным. Если произошло переполнение, то выведите «OVERFLOW!!!», иначе выведите полученное значение \(x\). Выходные данные Если во время выполнения \(f(0)\) произошло переполнение, то выведите «OVERFLOW!!!», иначе выведите полученное значение \(x\). Примечание В первом примере первая команда «add» выполнится 1 раз, вторая — 150 раз и последняя — 10 раз. Обратите внимание, что за «for \(n\)» может сразу следовать «end» и что «add» может быть расположен вне циклов for. Во втором примере нет команд «add», поэтому полученное значение равно 0. В третьем примере команда «add» выполняется слишком много раз, что делает значение \(x\) больше \(2^{32}-1\). | |
![]()
|
|
F. Keep talking and nobody explodes – easy
битмаски
Перебор
Разбор выражений
This is an unusual problem in an unusual contest, here is the announcement: http://cf.m27.workers.dev/blog/entry/73543 You have the safe lock which consists of 5 decimal digits. If you rotate some digit, it increases by one, except 9 which becomes 0. Initially, the lock contains number \(x\). To unlock the safe you must do the following operations in order (and be careful, don't mix up if and else statements). If sum of digits on positions 1 and 4 is greater than 10, rotate digit on position 1 by 3 times, else rotate digit on position 4 by 8 times. If sum of digits on positions 3 and 2 is greater than 8, rotate digit on position 4 by 9 times, else rotate digit on position 5 by 8 times. If digit on position 3 is odd, rotate digit on position 3 by 3 times, else rotate digit on position 3 by 4 times. If digit on position 5 is greater than digit on position 2, rotate digit on position 4 by 1 times, else rotate digit on position 2 by 7 times. If digit on position 1 is odd, rotate digit on position 1 by 3 times, else rotate digit on position 3 by 5 times. If digit on position 4 is odd, rotate digit on position 4 by 7 times, else rotate digit on position 1 by 9 times. If digit on position 4 is greater than digit on position 1, rotate digit on position 4 by 9 times, else rotate digit on position 4 by 2 times. If digit on position 1 is greater than digit on position 3, rotate digit on position 2 by 1 times, else rotate digit on position 3 by 1 times. If digit on position 5 is greater than digit on position 3, rotate digit on position 4 by 5 times, else rotate digit on position 5 by 8 times. If sum of digits on positions 1 and 3 is greater than 8, rotate digit on position 4 by 5 times, else rotate digit on position 2 by 5 times. If digit on position 1 is greater than digit on position 4, rotate digit on position 4 by 3 times, else rotate digit on position 2 by 3 times. If sum of digits on positions 3 and 1 is greater than 9, rotate digit on position 2 by 9 times, else rotate digit on position 2 by 2 times. If sum of digits on positions 4 and 3 is greater than 10, rotate digit on position 4 by 7 times, else rotate digit on position 5 by 7 times. If digit on position 3 is greater than digit on position 2, rotate digit on position 3 by 2 times, else rotate digit on position 4 by 6 times. If digit on position 1 is greater than digit on position 3, rotate digit on position 1 by 9 times, else rotate digit on position 2 by 9 times. If digit on position 3 is odd, rotate digit on position 3 by 9 times, else rotate digit on position 1 by 5 times. If sum of digits on positions 3 and 5 is greater than 9, rotate digit on position 3 by 4 times, else rotate digit on position 3 by 9 times. If digit on position 3 is greater than digit on position 1, rotate digit on position 5 by 1 times, else rotate digit on position 5 by 7 times. If digit on position 1 is greater than digit on position 3, rotate digit on position 2 by 9 times, else rotate digit on position 4 by 6 times. If sum of digits on positions 2 and 3 is greater than 10, rotate digit on position 2 by 2 times, else rotate digit on position 3 by 6 times. Output Output the number after applying all operations. | |
![]()
|
|
E. BHTML+BCSS
*особая задача
поиск в глубину и подобное
Разбор выражений
*2200
В этой задаче речь пойдет о вымышленных языках BHTML и BCSS, которые слегка напоминают HTML и CSS. Внимательно ознакомьтесь с условием задачи, так как схожесть лишь отдаленная, а в задаче используются крайне упрощенные аналоги. Задан BHTML-документ, который похож на HTML, но значительно проще. Записывается он как последовательность открывающих и закрывающих тегов. Тег вида «<имятега>» называется открывающим, а тег вида «</имятега>» — закрывающим. Кроме того, есть самозакрывающиеся теги, которые записываются в виде «<имятега/>» и в этой задаче полностью эквивалентны «<имятега></имятега>». Все имена тегов в этой задаче — строки из строчных латинских букв, имеющие длину от 1 до 10 символов. Некоторые теги могут иметь одинаковые имена. Теги в документе образуют правильную скобочную последовательность, то есть из заданной последовательности можно получить пустую с помощью операций: - удалить любой самозакрывающийся тег «<имятега/>»,
- удалить пару открывающий-закрывающий тег, которые идут подряд (в таком порядке) и имеют одинаковые имена, то есть подстроку «<имятега></имятега>».
Например, вам может быть задан документ «<header><p><a/><b></b></p></header><footer></footer>», но не могут быть заданы документы «<a>», «<a></b>», «</a><a>» или «<a><b></a></b>». Очевидно, для каждого открывающего тега существует единственный парный закрывающий — каждая такая пара называется элементом. Самозакрывающийся тег — тоже элемент. Говорят, что один элемент вложен в другой, если теги первого находятся между тегами второго. Считается, что никакой элемент не вложен сам в себя. Например, в примере выше элемент «b» вложен в «header» и в «p», но не вложен в «a» и «footer», а также не вложен в самого себя («b»). Элемент «header» имеет три вложенных в него элемента, а «footer» — ноль. Правила BCSS нужны для назначения стилей при выводе элементов документов BHTML. Каждое правило записывается в виде последовательностей слов «x1 x2 ... xn». Под это правило попадают все такие элементы t, которые удовлетворяют пунктам из списка: - существует последовательность вложенных элементов с именами тегов «x1», «x2», ..., «xn» (то есть второй элемент вложен в первый, третий во второй и так далее),
- эта последовательность заканчивается элементом t.
Например, правилу «a b» удовлетворяют все такие элементы «b» для которых существует элемент «a», в который они вложены. Правилу «a b b c» удовлетворяют все такие элементы «c» для которых существует три элемента «a», «b», «b», что в цепочке «a»-«b»-«b»-«c» каждый очередной элемент вложен в предыдущий. Напишите программу, которая по заданному BHTML-документу и набору BCSS-правил определяет количество элементов, которые удовлетворяют каждому из правил. Выходные данные Выведите m строк, j-ая строка должна содержать количество элементов документа, которые соответствуют j-ому BCSS-правилу. Если таких элементов вообще нет, то выведите в строку 0. | |
![]()
|
|
H. Стек
*особая задача
Разбор выражений
реализация
*1800
Рассмотрим стек, который поддерживает выполнение двух типов действий: - Добавить заданное число в стек.
- Извлечь два числа из стека, произвести над ними арифметическую операцию (сложение или умножение) и добавить результат этой арифметической операции в стек.
Вам задана строка, описывающая последовательность действий над стеком. i-ый символ строки соответствует i-ому действию, которое надо выполнить: - Если i-й символ является цифрой, то нужно добавить в стек число, соответствующее этой цифре.
- Если i-й символ «+» или «*», то нужно выполнить арифметическую операцию, соответствующую этому символу.
Изначально стек пуст. Выведите число, которое окажется на вершине стека после выполнения всех заданных действий. Выходные данные Выведите единственное число — верхний элемент стека после выполнения заданных операций. Примечание В первом примере действия над стеком эквивалентны вычислению выражения (1+2)*3+6*6. Во втором примере используется только добавление чисел в стек, и ответом будет последнее добавленное число. | |
![]()
|
|
C. Попробуй поймай
Разбор выражений
реализация
*1800
Вася разрабатывает свой язык программирования VPL (Vasya Programming Language). Сейчас он занят созданием системы исключений. В его представлении система исключений должна функционировать следующим образом. Для обработки исключений используются try-catch-блоки. Работа с блоками осуществляется при помощи двух операторов: - Оператор try. Открывает новый try-catch-блок.
- Оператор catch(<тип_исключения>, <сообщение>). Закрывает еще не закрытый try-catch-блок, который был начат последним. Данный блок может быть активирован только исключением типа <тип_исключения>. При активации этого блока, на экран выводится <сообщение>. Если в данный момент не открыто ни одного try-catch-блока, то оператор catch использовать нельзя.
Исключения могут возникать в программе только в одном случае: при использовании оператора throw. Оператор throw(<тип_исключения>) создает исключение указанного типа. Пусть в результате вызова какого-то оператора throw в программе возникло исключение типа a. В этом случае активируется try-catch-блок такой, что оператор try этого блока описан в программе раньше, чем вызванный оператор throw, при этом оператору catch этого блока в качестве параметра передан тип исключения a, и оператор catch этого блока описан позже, чем вызванный оператор throw. Если таких try-catch-блоков несколько, активируется тот блок, описание оператора catch которого встречается раньше всех. Если ни один try-catch-блок не был активирован, то на экран выводится сообщение «Unhandled Exception». Для тестирования системы, Вася составил программу, в которой содержатся только операторы try, catch и throw, в одной строке находится не более одного оператора, во всей программе присутствует ровно один оператор throw. Ваша задача в том, чтобы по программе на VPL определить, какое сообщение будет выведено на экран. Выходные данные Выведите сообщение, которое будет написано на экране после выполнения заданной программы. Примечание В первом примере существует 2 try-catch блока, для которых оператор try описан раньше оператора throw, а оператор catch описан позже оператора throw: try-catch(BE,"BE in line 3") и try-catch(AE,"AE somewhere"). Тип исключения AE, а значит будет активирован второй блок, так как в операторе catch(AE,"AE somewhere") указан тип исключения AE, а в операторе catch(BE,"BE in line 3") указан тип BE. Во втором примере существует 2 try-catch блока, для которых оператор try описан раньше оператора throw, а оператор catch описан позже оператора throw: try-catch(AE,"AE in line 3") и try-catch(AE,"AE somewhere"). В данном случае оба блока могут быть активированы исключением типа AE, но будет активирован только блок try-catch(AE,"AE in line 3"), так как оператор catch(AE,"AE in line 3") описан раньше, чем catch(AE,"AE somewhere"). В третьем примере не существует блоков, способных обработать исключение типа CE. | |
![]()
|
|
J. Помогите, что значит быть «Based»
*особая задача
Конструктив
Перебор
Разбор выражений
реализация
сортировки
Выходные данные Если \(x = 1\), выдай код, который, типа, когда подаёшь ему два целых числа \(a\) и \(b\), он возвращает их сумму. Если \(x = 2\), напиши код, который принимает целое число \(a\) и возвращает его абсолютное значение, как будто волшебство, без всяких приколов. Если \(x = 3\), чекай это: сочини код, который берёт целое число \(n\) (\(1 \le n \le 50\)) и массив \(a\) из \(n\) различных целых чисел, а потом возвращает максимальное значение, вжух! Если \(x = 4\), бросай код, который берёт целое число \(n\) (\(1 \le n \le 50\)), массив \(a\) из \(n\) различных целых чисел и целое число \(k\) (\(1 \le k \le n\)), а потом выдаёт \(k\)-тое по величине значение в массиве. Врубился, братишка?! Примечание Загляни на страницу «Мои посылки» и оцени свой код, кликнув на его ID. Ты увидишь, насколько based или cringe он. | |
![]()
|
|
D. Язык программирования
Бинарный поиск
Перебор
Разбор выражений
реализация
*1800
Недавно Валерий познакомился с совершенно новым языком программирования. Больше всего в этом языке его привлекли шаблонные функции и процедуры. Напомним, что шаблонами называются средства языка, предназначенные для кодирования обобщённых алгоритмов, без привязки к некоторым параметрам (например, типам данных, размерам буферов, значениям по умолчанию). Валерий решил более подробно изучить шаблонные процедуры этого языка. Описание шаблонной процедуры состоит из имени процедуры и списка типов ее параметров. В качестве параметров шаблонных процедур могут использоваться параметры обобщенного типа T. Вызов процедуры состоит из имени процедуры и списка переменных-параметров. Назовем процедуру подходящей для данного вызова, если выполняются условия: - ее имя совпадает с именем вызванной процедуры;
- количество ее параметров совпадает с количеством параметров вызванной процедуры;
- типы ее параметров совпадают с соответствующими типами переменных в вызове процедуры. Тип параметра совпадает с типом переменной, если параметр имеет обобщенный тип T, либо типы переменной и параметра совпадают.
Вам дано описание некоторого набора шаблонных процедур. Также дан список переменных, используемых в программе, а также непосредственные вызовы процедур с использованием описанных переменных. Для каждого вызова от Вас требуется посчитать количество процедур, подходящих данному вызову. Входные данные В первой строке задано единственное целое число n (1 ≤ n ≤ 1000) — количество шаблонных процедур. Далее в n строках задано описание процедур, в следующем формате: «void procedureName (type_1, type_2, ..., type_t)» (1 ≤ t ≤ 5), где void — ключевое слово, procedureName — имя процедуры, type_i — тип очередного параметра. Типами параметров языка могут являться «int», «string», «double», а также ключевое слово «T», которое обозначает обобщенный тип. В следующей строке задано единственное целое число m (1 ≤ m ≤ 1000) — количество используемых переменных. Далее в m строках задано описание переменных, в следующем формате: «type variableName», где type — тип переменной, который может принимать значения «int», «string», «double», variableName — имя переменной. В следующей строке задано единственное целое число k (1 ≤ k ≤ 1000) — количество вызовов процедур. Далее в k строках заданы вызовы процедур в следующем формате: «procedureName (var_1, var_2, ..., var_t)» (1 ≤ t ≤ 5), где procedureName — имя процедуры, var_i — имя очередной переменной. В строках описания переменных, шаблонных процедур и их вызовов могут присутствовать пробелы в начале строки, в конце строки, перед и после скобок и запятых. Пробелы могут присутствовать до и после ключевого слова void. Длина каждой строки входных данных не превосходит 100 символов. Имена переменных и процедур являются непустыми строками из латинских строчных букв и цифр длиной не более 10 символов. Отметим, что это — единственное ограничение на имена переменных и процедур. В вызовах процедур используются только описанные переменные. Имена переменных различны. Никакие две процедуры не совпадают. Две процедуры совпадают, если они имеют одинаковые имена, а также упорядоченные наборы типов их параметров совпадают. Выходные данные В каждую из k строк выведите единственное число. Число в i-ой строке означает количество подходящих шаблонных процедур под i-ый вызов. Вызовы нумеруются в том порядке, в котором они заданы во входных данных. | |
![]()
|
|
C. Формуроса
дп
Разбор выражений
разделяй и властвуй
*2600
Байтляндский Институт Биологических Исследований (БИБИ) изучает свойства двух видов бактерий, названных 0 и 1. Даже под микроскопом бактерии этих двух видов очень трудно отличить. Вобщем-то, у ученых есть только один способ, который способен различать их — это растение под названием Формуроса. Если ученые поместят по образцу колоний бактерий на каждом листке Формуросы, активируется сложный процесс питания растения. Во время этого процесса цвет Формуросы изменится, в соответствии с, возможно, очень сложной логической формулой, включающей константы и операторы | (OR), & (AND) и ^ (XOR). Если результат подсчета формулы равен 0, то растение покраснеет, в противном случае посинеет. Например, если процесс питания Формуросы описывается формулой: (((?^?)|?)&(1^?)), то у Формуросы есть четыре листа (знаки «?» обозначают листья). Если мы положим образцы бактерий 0, 1, 0, 0 на соответствующие листья, результатом питательного процесса будет (((0^1)|0)&(1^0)) = 1, следовательно, растение посинеет. У ученых есть n колоний бактерий. Они не знают их типы; они знают наверняка только то, что не все колонии одного типа. Ученые хотят попытаться определить виды бактерий, с помощью нескольких экспериментов с Формуросой. Во время каждого эксперимента ученые должны поместить ровно по одному образцу на каждый лист растения. Тем не менее, они могут использовать несколько образцов из одной колонии в течение одного эксперимента; например, можно покрыть все листья растения бактериями из одной колонии! Смогут ли ученые определить вид каждой колонии, какими бы эти колонии ни были (если предположить, что не все колонии одинаковые)? Выходные данные Если всегда возможно определить вид каждой колонии, выведите «YES» (без кавычек). В противном случае выведите «NO» (без кавычек). | |
![]()
|
|
A. Скобочная последовательность
Разбор выражений
реализация
Структуры данных
*1700
Скобочной последовательностью называется строка, состоящая только из символов «(», «)», «[» и «]». Правильной скобочной последовательностью называется скобочная последовательность, которую можно преобразовать в корректное арифметическое выражение путем вставок между ее символами символов «1» и «+». Например, скобочные последовательности «()[]», «([])» — правильные (полученные выражения: «(1)+[1]», «([1+1]+1)»), а «](» и «[» — нет. Пустая строка является правильной скобочной последовательностью по определению. Подстрокой s[l... r] (1 ≤ l ≤ r ≤ |s|) строки s = s1s2... s|s| (где |s| — длина строки s) называется строка slsl + 1... sr. Пустая подстрока по определению считается подстрокой любой строки. Вам дана не обязательно правильная скобочная последовательность. Найдите ее подстроку, которая является правильной скобочной последовательностью и при этом содержит как можно больше скобок «[». Выходные данные В первой строке выведите единственное целое число — количество скобок «[» в оптимальной подстроке. Во второй строке выведите саму подстроку. Если существует несколько оптимальных подстрок выведите любую. | |
![]()
|
|
B. Азбука Борзе
Разбор выражений
реализация
*800
Сейчас в Берляндии популярна троичная система счисления. Для телеграфной передачи чисел, записанных в троичной системе счисления, используется азбука Борзе. Цифра 0 передается как «.», 1 как «-.», 2 как «--». Расшифровка кода Борзе чисел — очень важная и ответственная работа. Ваша задача — расшифровать заданное в коде Борзе троичное число. Выходные данные Выведите расшифровку заданного кода Борзе. Расшифрованное число может содержать лидирующие нули. | |
![]()
|
|
C. Список
Разбор выражений
реализация
сортировки
Строки
*1300
Компания «Bersoft» работает над новой версией своего самого известного текстового редактора, Bord 2010. В Bord, как и во многих других текстовых редакторах, должна быть реализована возможность печати многостраничных документов. Пользователь перечисляет через запятую (без пробелов) номера страниц документа, которые он хочет распечатать. Вам поручено написать часть программы, выполняющую «нормализацию» списка. На вход вашей программе подается список, который ввел пользователь. Ваша программа должна вывести этот список в формате l1-r1,l2-r2,...,lk-rk, где ri + 1 < li + 1 для всех i от 1 до k - 1, и li ≤ ri. Новый список должен содержать все страницы которые ввел пользователь и ничего больше. Повторные появлений одной и той же страницы в списке пользователя следует игнорировать. В случае, если для некоторого элемента i нового списка li = ri, этот элемент необходимо выводить как li, а не «li - li». Например, список 1,2,3,1,1,2,6,6,2 нужно вывести в виде 1-3,6. Выходные данные Выведите список в требуемом формате. | |
![]()
|
|
A. Вычисления в C*++
жадные алгоритмы
Разбор выражений
*2000
Язык C*++ похож на C++. Это сходство проявляется в том, что программы на C*++ порой ведут себя непредсказуемо и приводят к совершенно неожиданным эффектам. Например, представим себе арифметическое выражение на C*++, имеющее следующий вид: - expression ::= summand | expression + summand | expression - summand
- summand ::= increment | coefficient*increment
- increment ::= a++ | ++a
- coefficient ::= 0|1|2|...|1000
Например, 5*a++-3*++a+a++ — это корректное арифметическое выражение на C*++. Итак, мы имеем сумму, состоящую из нескольких слагаемых, разделенных знаками «+» или «-». Каждое слагаемое представляет собой выражение «a++» или «++a», умноженное на некоторый целый коэффициент. Если коэффициент опущен, то предполагается, что он равен 1. Вычисление такой суммы в C*++ происходит следующим образом. Сначала по очереди вычисляются все слагаемые, после этого происходит суммирование по обычным арифметическим правилам. Если слагаемое содержит «a++», то при его вычислении сначала происходит умножение значения переменной «a» на коэффициент, затем значение «a» увеличивается на 1. Если слагаемое содержит «++a», то действия над ним выполняются в обратном порядке: сначала — увеличение «a» на 1, затем — умножение на коэффициент. Порядок вычисления слагаемых может быть любым, поэтому иногда результат вычисления выражения совершенно непредсказуем! Ваша задача — найти наибольшее возможное его значение. Выходные данные Выведите единственное число — наибольшее возможное значение выражения. Примечание Рассмотрим второй пример. Сначала a = 3. Пусть сначала вычисляется первое слагаемое, потом — второе. Первое слагаемое получается равным 3, и значение a увеличивается на 1. При вычислении второго слагаемого значение a сначала еще раз увеличивается (становится равным 5). Значение второго слагаемого — 5, и в сумме получаем 8. При вычислении сначала второго, а потом первого слагаемого получаем, что оба слагаемых равны 4 и ответ тоже 8. | |
![]()
|
|
C. Email-адрес
Разбор выражений
реализация
*1300
Иногда email-адреса приходится диктовать по телефону. Точку обычно называют словом dot, а собаку at. В результате получается что-то вроде vasyaatgmaildotcom. Ваша задача — преобразовать это в корректный email-адрес ([email protected]). Известно, что корректный email-адрес содержит только символы . @ и маленькие латинские буквы, не начинается и не заканчивается точкой. Также, корректный email-адрес не начинается и не заканчивается собакой. Более того, email-адрес содержит ровно один символ @ но при этом может содержать любое (возможно, нулевое) количество точек. Требуется произвести серию замен, чтобы длина результата оказалась как можно меньше, и он являлся корректным email-адресом. При равенстве длин нужно вывести лексикографически минимальный результат. Всего возможно два варианта замены: dot можно заменить на точку, at можно заменить на собаку. Выходные данные Выведите кратчайший email-адрес, из которого могла быть получена указанная строка путем указанных выше замен. Если решений несколько, выведите лексикографически минимальное (лексикографическое сравнение строк реализует оператор < в современных языках программирования). Символы идут в таблице ASCII в следующем порядке: . @ ab...z | |
![]()
|
|
B. Анализ таблиц bHTML
Разбор выражений
*1700
В этой задаче используется крайне упрощенный вариант разметки таблиц средствами HTML. Пожалуйста, используйте условие как формальный документ. Строка определяет таблицу bHTML, если имеет вид:
TABLE ::= <table>ROWS</table>
ROWS ::= ROW | ROW ROWS
ROW ::= <tr>CELLS</tr>
CELLS ::= CELL | CELL CELLS
CELL ::= <td></td> | <td>TABLE</td>
Пробелы в грамматике заданы исключительно для наглядности, при записи таблиц они не используются. Иными словами, таблицы в bHTML очень похожи на обычные таблицы HTML в которых только участвуют теги «table», «tr», «td», все теги парные и таблица содержит хотя бы одну строку и хотя бы одну ячейку в каждой строке. Посмотрите тесты из условия в качестве примеров таблиц. Как видно, таблицы могут вкладываться друг в друга. Вам задана одна таблица (в которую, возможно, вложены другие). Вам надо написать программу, которая проанализирует все таблицы и найдет для каждой из них количество ее ячеек. Таблицы не обязаны быть прямоугольными. Выходные данные Выведите размеры всех таблиц во входных данных в порядке неубывания. | |
![]()
|
|
E. Ваня и скобки
дп
жадные алгоритмы
Перебор
Разбор выражений
реализация
Строки
*2100
Ваня делает домашнее задание по математике. У него есть выражение типа  , где x1, x2, ..., xn — цифры от 1 до 9, а знаком , где x1, x2, ..., xn — цифры от 1 до 9, а знаком  обозначается либо плюс '+' либо знак умножения '*'. Ване нужно поставить в этом выражении одну пару скобок так, чтобы максимизировать значение полученного выражения. обозначается либо плюс '+' либо знак умножения '*'. Ване нужно поставить в этом выражении одну пару скобок так, чтобы максимизировать значение полученного выражения. Выходные данные В первой строке выведите максимальное возможное значение выражения. Примечание Пояснение к первому тесту из условия. 3 + 5 * (7 + 8) * 4 = 303. Пояснение к второму тесту из условия. (2 + 3) * 5 = 25. Пояснение к третьему тесту из условия. (3 * 4) * 5 = 60 (также подходит множество других вариантов, например, (3) * 4 * 5 = 60). | |
![]()
|
|
C. Почта в корпорации
Разбор выражений
реализация
Структуры данных
*1700
Структура корпорации Бернефть имеет иерархический вид, то есть может быть представлена в виде дерева. Рассмотрим представление этой структуры в следующем виде: - employee ::= name. | name:employee1,employee2, ... ,employeek.
- name ::= имя сотрудника
То есть описание каждого сотрудника состоит из его имени, двоеточия, описаний всех его подчиненных, разделённых запятыми, и точки в конце. Если у сотрудника нет подчиненных, двоеточие в его описании отсутствует. Например, строка MIKE:MAX.,ARTEM:MIKE..,DMITRY:DMITRY.,DMITRY... является корректной записью структуры корпорации, в которой директор MIKE имеет подчиненных MAX, ARTEM и DMITRY. ARTEM имеет подчиненного, которого зовут MIKE, точно так же как и его начальника, а двоих подчиненных DMITRY зовут DMITRY, как и его самого. В корпорации Бернефть каждый сотрудник может переписываться только со своими подчиненными, причем не обязательно прямыми. Назовем неудобной ситуацию, когда человек с именем s пишет письмо другому человеку, которого так же зовут s. В приведенном выше примере есть 3 таких пары: одна с участием MIKE, и две для DMITRY (по одной на каждого его подчиненного). Ваша задача — по заданной структуре корпорации найти количество неудобных пар в ней.  Выходные данные Выведите одно число — количество неудобных ситуаций в корпорации. | |
![]()
|
|
E. Булева функция
битмаски
дп
Разбор выражений
*3000
В данной задаче рассматриваются булевы функции от четырех переменных A, B, С, D. Переменные A, B, C и D являются логическими и могут принимать значения 0 или 1. Будем задавать функцию с помощью следующей грамматики: <выражение> ::= <переменная> | (<выражение>) <оператор> (<выражение>) <переменная> ::= 'A' | 'B' | 'C' | 'D' | 'a' | 'b' | 'c' | 'd' <оператор> ::= '&' | '|' Здесь заглавными буквами A, B, C, D обозначаются переменные, а строчными — их отрицания. Например, если A = 1, то символу 'A' соответствует значение 1, а символу 'a' — значение 0. Символ '&' здесь соответствует операции логического И, символ '|' — операции логического ИЛИ. Вам дано выражение s, задающее функцию f, в котором некоторые операторы и переменные пропущены. Так же вам известны значения функции f(A, B, C, D) для некоторых n различных наборов значений переменных. Посчитайте количество способов восстановить пропущенные в выражении элементы так, чтобы получившееся выражение соответствовало известной информации о функии f в заданных наборах переменных. Так как величина результата может быть большой, выведите её остаток от деления на 109 + 7. Выходные данные В единственной строке выведите ответ на задачу. Примечание В первом примере двумя подходящими выражением являются 'C' и 'd'. Во втором примере выражения выглядят так: '(A)&(a)', '(A)&(b)', '(A)&(C)', '(A)&(D)'. | |
![]()
|
|
C. Название
Разбор выражений
*1600
Недавно Вася закончил писать книгу. Теперь перед ним стоит проблема выбора названия. Вася хочет, чтобы название было непонятным и загадочным, чтобы его книга выделялась на фоне других. Поэтому название должно представлять собой одно слово, в котором содержится хотя бы один раз каждая из k первых букв латинского алфавита, и не содержатся никакие другие. Так же название должно быть палиндромом, то есть читаться одинаково как слева направо, так и справа налево. Вася уже составил примерный вариант названия. Вам задан шаблон названия s, состоящий из маленьких латинских букв и знаков вопроса. Ваша задача — заменить в шаблоне все знаки вопроса на маленькие латинские буквы так, чтобы получившееся название соответствовало описанным выше требованиям. Каждый вопрос нужно заменить ровно одной буквой, удалять и добавлять новые символы в шаблон не разрешается. Если подходящих названий несколько, выберите первое в алфавитном порядке, чтобы Васина книга встречалась как можно раньше во всех каталогах. Выходные данные Если решения не существует, выведите IMPOSSIBLE. Иначе в единственной строке должно содержаться искомое название, соответствующее заданному шаблону. Это название должно быть палиндромом, и в нем могут встречаться только первые k букв латинского алфавита, причем каждая из этих k букв должна встречаться хотя бы один раз. Если подходящих названий несколько, выведите лексикографически наименьшее. Лексикографическое сравнение реализует оператор < в современных языках программирования. Строка a лексикографически меньше строки b, если существует такое i (1 ≤ i ≤ |s|), что ai < bi, а для любого j (1 ≤ j < i) aj = bj. |s| обозначает длину заданного шаблона. | |
![]()
|
|
C. Заменить до правильной скобочной последовательности
математика
Разбор выражений
Структуры данных
*1400
Вам задана строка s, состоящая из открывающих и закрывающих скобок четырех видов <>, {}, [], (). Все скобки делятся на два типа: открывающие и закрывающие. Разрешается заменить любую скобку на любую другую такого же типа. Например, скобку < можно заменить на скобку {, но нельзя заменить на скобку ) или >. Далее приводится стандартное определение правильной скобочной последовательности, с которым вы возможно уже знакомы. Определим правильную скобочную последовательность. Пустая строка считается таковой. Пусть строки s1 и s2 являются правильными скобочными последовательностями, тогда строки <s1>s2, {s1}s2, [s1]s2, (s1)s2 также являются правильными скобочными последовательностями. Например, строка "[[(){}]<>]" является правильной скобочной последовательностью, а строки "[)()" и "][()()" — нет. Определите наименьшее количество замен, необходимое для того, чтобы сделать строку s правильной скобочной последовательностью. Выходные данные Если получить правильную скобочную последовательность из строки s невозможно выведите слово Impossible. Иначе выведите наименьшее количество замен, необходимое для получения правильной скобочной последовательности из строки s. | |
![]()
|
|
B. Выражение
*особая задача
Разбор выражений
*1500
Задана строка вида «n#m», где «n» и «m» это цифры, а «#» это знак «+» или «-». Требуется вывести значение этого выражения. Выходные данные Выведите значение выражения. | |
![]()
|
|
F. Проверка домена
*особая задача
Разбор выражений
*2000
Данная задача не содержит сведений из реальных спецификаций, используйте текст условия задачи как формальный документ, недвусмысленно описывающий то, что надо сделать. Будем считать, что строка определяет имя домена, если она состоит из символов «a»-«z», «0»-«9» и точек. Никакие две точки не должны в имени домена идти подряд. Пусть точками вся строка разделяется на части — тогда последняя часть (самая правая) должна иметь длину 2 или 3. Начинаться и заканчиваться точкой имя домена не может. Определите, является ли заданная строка именем домена. Выходные данные Выведите «YES» или «NO» в зависимости от того, является ли заданная строка именем домена. | |
![]()
|
|
A. Ребус
жадные алгоритмы
Конструктив
математика
Разбор выражений
*1800
Вам дан ребус вида ? + ? - ? + ? = n, то есть состоящий из знаков вопроса, разделённых знаками «+» и «-», знака равенства и целого положительного числа n. Требуется заменить каждый из знаков вопроса на целое число от 1 до n так, чтобы равенство выполнялось. Выходные данные В первой строке выходных данных выведите «Possible» (без кавычек), если ребус имеет решение, и «Impossible» (без кавычек) в противном случае. Если решение ребуса существует, то во второй строке выведите ребус, в котором вопросики заменены на целые числа от 1 до n. Следуйте формату, используемому в примерах. | |
![]()
|
|
E. Проверка макросов
дп
Разбор выражений
реализация
*2600
Большинство программистов на C/C++ знают об отличных возможностях, предоставляемых директивами препроцессора #define, но также многим известны и проблемы, возникающие при их неаккуратном использовании. В данной задаче мы рассматриваем следующую модель конструкций #define (также называемых макросами). Каждый макрос имеет свои имя и значение. Объявляется он следующим образом: #define имя_макроса значение_макроса После этого объявления везде, где в программе встречается слово "имя_макроса" (как отдельный токен, т.е. как подстрока, окружённая неалфавитными символами), оно заменяется на "значение_макроса". В "значение_макроса" в рамках нашей модели может быть записано только какое-либо арифметическое выражение, содержащее переменные, четыре арифметических операции, скобки, а также имя ранее объявленных макросов (в этом случае замена производится по цепочке). Процесс замены макросов на их значения называется подстановкой. Одна из основных проблем, возникающих при использовании макросов — когда после выполнения подстановки получается арифметическое выражение, в котором из-за разных приоритетов операций может неожиданно измениться порядок вычисления. Рассмотрим это на следующем примере. Определим такую конструкцию #define: #define sum x + y и пусть далее в программе считается выражение "2 * sum". После подстановки макроса получится выражение "2 * x + y", вместо интуитивно ожидаемого "2 * (x + y)". Определим "подозрительной" ситуацию, когда после выполнения подстановки макроса порядок вычислений меняется, выходя за пределы какого-либо макроса. Соответственно, Ваша задача — по набору определений #define и заданному выражению определить, является это выражение подозрительным или нет. Определим это более формально. Выполним обычную подстановку макросов в заданном выражении. Кроме того, выполним "безопасную" подстановку макросов в выражение: окружив значение каждого макроса скобками; после этого, пользуясь арифметическими правилами раскрытия скобок, можно опустить некоторые скобки. Если при этом можно получить выражение, полностью совпадающее с результатом обычной подстановки (посимвольно, но игнорируя пробелы), то это выражение и система макросов считаются корректными, иначе — подозрительными. Примечание. В этом критерии операция деления рассматривается с математической точки зрения, а не в смысле языка C++ (в котором под ним подразумевается деление нацело). Например, в выражении "a*(b/c)" мы можем опустить скобки и получить выражение "a*b/c". Выходные данные Выведите строку "OK", если выражение корректно с точки зрения критерия, описанного в условии, иначе выведите "Suspicious". | |
![]()
|
|
B. SMS
жадные алгоритмы
Разбор выражений
Строки
*1600
Маленький морж Клычок, как и все современные моржи, любит общаться с помощью SMS. Однажды он столкнулся с проблемой, что при отправке больших текстов они разделяются на части по n символов (размер одного SMS сообщения), и разрываются целые предложения или даже слова! Клычку это не понравилось, и перед ним встала задача разбить текст на сообщения самостоятельно таким образом, чтобы ни одно предложение не было разбито на части при отправке, и количество SMS сообщений для отправки было бы минимальным. Если два подряд идущих предложения находятся в разных сообщениях, то пробел между ними можно не учитывать (Клычок этот пробел не набирает). Текст маленького моржа имеет следующий вид: TEXT ::= SENTENCE | SENTENCE SPACE TEXT
SENTENCE ::= WORD SPACE SENTENCE | WORD END
END ::= {'.', '?', '!'}
WORD ::= LETTER | LETTER WORD
LETTER ::= {'a'..'z', 'A'..'Z'}
SPACE ::= ' '
Под SPACE следует подразумевать символ пробела. Сколько же сообщений отправил Клычок? Выходные данные В первой и единственной строке выведите количество SMS сообщений, которое потребуется Клычку. Если разбить текст невозможно, выведите "Impossible" без кавычек. Примечание Рассмотрим третий пример. Текст будет разбит на 3 сообщения: "Hello!", "Do you like fish?" и "Why?". | |
![]()
|
|
D. Perse-script
*особая задача
Разбор выражений
*2300
Два друга решили создать язык программирования, назвали они его Perse-script. Важная часть языка — строки. Строки в Perse-script записываются в кавычках (") Например, "Hello" — константная строка. Но Hello — имя переменной или зарезервированное слово, которые мы не рассматриваем в этой задаче. Perse-script — функциональный язык, в нем нет операторов. Например, чтобы сложить два числа нужно написать sum(a,b), а не a+b. В языке есть несколько команд для работы со строками: - concat(x,y) возвращает конкатенацию («склейку») двух строк x и y. Например, concat("Hello","World") возвращает "HelloWorld".
- reverse(x) возвращает перевернутую строку x. Например, reverse("Hello") возвращает "olleH".
- substr(x,a,b) принимает строку x и два целых числа a и b (1 ≤ a ≤ b ≤ n, где n — длина строки x). Возвращает подстроку x с индекса a по индекс b, включительно. Например, substr("Hello",2,4) возвращает "ell".
- substr(x,a,b,c) — другая версия substr, которая получает подстроку с шагом c. c всегда положительно. Например, substr("HelloWorld",1,10,2) возвращает "Hlool". Более точно: изначально ответ пуст. Эта функция добавляет в ответ a-ый символ, а затем каждый c-ый считая от него, и так до b.
Вы собираетесь реализовать работу со строками в Perse-script. Дано выражение, выведите его результат. Гарантируется, что все функции в качестве аргументов содержат только константные строки, записанные в кавычках, и перечисленные выше строковые функции. Названия функций Perse-script регистронезависимы. Так, чтобы вызвать substr можно написать SUBsTr(). Но нельзя писать "hElLo" вместо "Hello". Для дальнейшего разъяснения смотрите примеры. Выходные данные В единственной строке выведите результат. Гарантируется, что ответ существует, и его длина не превосходит 104. Гарантируется, что ответ не является пустой строкой. | |
![]()
|
|
B. Анализ текстового документа
Разбор выражений
реализация
Строки
*1100
Современные текстовые редакторы обычно показывают некоторую информацию для текущего редактируемого документа — например, количество слов, количество страниц или количество знаков. В этой задаче вам предстоит реализовать похожую функциональность. Задана строка, состоящая только из: - прописных и строчных букв английского алфавита,
- символов подчёркивания (они используются в качестве разделителей),
- круглых скобок (как открывающих, так и закрывающих).
Гарантируется, что каждая открывающая скобка имеет парную закрывающую, идущую следом. Аналогично, каждая закрывающая скобка имеет парную открывающую, которая расположена до неё. Для каждой пары соответствующих скобок верно, что между ними нет каких-либо других скобок. Иными словами, каждая скобка в строке входит в пару «открывающая-закрывающая», и такие пары не вкладываются друг в друга. Например, допустимой строкой является: «_Hello_Vasya(and_Petya)__bye_(and_OK)». Словом называется нерасширяемая последовательность подряд идущих букв, то есть последовательность букв, такая что слева и справа от неё находится скобка или символ подчёркивания, или соответствующий символ отсутствует. Пример выше содержит семь слов: «Hello», «Vasya», «and», «Petya», «bye», «and» и «OK». Напишите программу, которая найдет: - длину самого длинного слова вне скобок (выведите 0, если слов вне скобок нет),
- количество слов внутри скобок (выведите 0, если слов внутри скобок нет).
Выходные данные Выведите два числа: - длину самого длинного слова вне скобок (выведите 0, если слов вне скобок нет),
- количество слов внутри скобок (выведите 0, если слов внутри скобок нет).
Примечание В первом примере слова «Hello», «Vasya» и «bye» записаны вне скобок, а слова «and», «Petya», «and» и «OK» — внутри. Обратите внимание, что слово «and» встречается дважды, и учитывать в ответе его тоже следует два раза. | |
![]()
|
|
B. Сумма чека
Разбор выражений
реализация
Строки
*1600
Василий вышел из магазина и ему стало интересно пересчитать сумму в чеке. Чек представляет собой строку, в которой названия покупок и их цены записаны подряд без пробелов. Чек имеет вид «name1price1name2price2...namenpricen», где namei (название i-го продукта) — это непустая строка длины не более 10, состоящая из строчных букв латинского алфавита, а pricei (цена i-го продукта) — это непустая строка, состоящая из точек и цифр. Продукты с одинаковым названием могут иметь разные цены. Цена каждого продукта записана в следующем формате. Если продукт стоит целое количество рублей, то копейки не пишутся. Иначе, после записи количества рублей к цене приписывается точка, за которой следом ровно двумя цифрами записаны копейки (если копеек менее 10, то используется лидирующий ноль). Также, каждые три разряда (от менее значимых к более значимым) в записи рублей разделяются точками. Лишние лидирующие нули недопустимы, запись цены всегда начинается с цифры и заканчивается цифрой. Например, записи цен: - «234», «1.544», «149.431.10», «0.99» и «123.05» являются корректными,
- «.333», «3.33.11», «12.00», «.33», «0.1234» и «1.2» не являются корректными.
Напишите программу, которая по содержимому чека найдет суммарную цену всех покупок. Выходные данные Выведите суммарную цену всех покупок строго в том же формате, в котором задаются цены покупок во входных данных. | |
![]()
|
|
E. Комментарии
поиск в глубину и подобное
Разбор выражений
реализация
Строки
*1700
Редкая статья в интернете обходится без возможности комментирования. Вот и на сайте, который написал Поликарп, у каждой статьи есть лента комментариев. Каждый комментарий на сайте Поликарпа — это непустая строка из строчных или прописных латинских букв. Комментарии имеют древовидную структуру, то есть у каждого комментария, кроме корневых (то есть комментариев самого верхнего уровня) есть ровно один родительский комментарий. При сохранении комментариев на жесткий диск Поликарп использует следующий формат. Каждый комментарий он записывает так: - сначала следует текст комментария;
- затем следует количество комментариев, для которых он является родительским (то есть тех, которые даны в ответ на этот комментарий);
- после этого следуют комментарии, для которых этот является родительским (запись комментариев происходит по такому же алгоритму).
Все элементы в записи выше разделяются единичными запятыми. Аналогично, комментарии первого уровня Поликарп записывает через запятую. Например, если комментарии имели вид:  то первый будет записан как «hello,2,ok,0,bye,0», второй как «test,0», а третий как «one,1,two,2,a,0,b,0». Вся ветка комментариев будет записана как: «hello,2,ok,0,bye,0,test,0,one,1,two,2,a,0,b,0». По заданной ветке комментариев в формате описанном выше выведите комментарии в другом формате: - сначала выведите d — максимальную глубину вложенности комментариев;
- затем выведите d строк, i-я из них соответствует комментариям вложенности i;
- для i-й строки выведите комментарии вложенности i в порядке их появления в записи Поликарпа, разделённые единичными пробелами.
Выходные данные Выведите комментарии в формате, описанном в условии. Для каждого уровня вложенности комментарии выводите в том же порядке, в котором они заданы во входных данных. Примечание Первый пример разобран в условии. | |
![]()
|
|
B. Стена Facetook
Разбор выражений
реализация
Строки
*1500
Facetook — широко известная социальная сеть. Недавно в ней появилась новая функция — стена с приоритетами. Эта функция позволяет сортировать всех ваших друзей по коэффициенту дружбы. Чем больше вы общаетесь с другом, тем больше будет его коэффициент дружбы. На коэффициент дружбы влияет 3 типа действий: - 1. человек X написал на стене человек Y ("X posted on Y's wall") — 15 очков;
- 2. человек X прокомментировал сообщение человека Y ("X commented on Y's post") — 10 очков;
- 3. человеку X понравилось сообщение человека Y ("X likes Y's post") — 5 очков.
X и Y — два различных имени. Каждое действие увеличивает коэффициент дружбы между X и Y (и наоборот) на данное количество очков (коэффициент дружбы между X и Y равен коэффициенту дружбы между Y и X). Вам дано n действий в формате, описанном выше. Выведите все различные имена, которые встречаются в списке действий, в отсортированном порядке в соответствие с коэффициентом дружбы с вами. Выходные данные Выведите m строк, где m — количество различных имен во входных данных (исключая вас). Каждая строка должна содержать ровно одно имя. Имена должны быть отсортированы в по убыванию коэффициента дружбы с вами (т. е. люди с большим коэффициентом дружбы должны идти раньше). Если два или больше человек имеют одинаковый коэффициент дружбы, выводите их в алфавитном (лексикографическом) порядке. Учтите, что нужно выводить все имена, присутствующие во входных данных (исключая вас), даже если человек имеет нулевой коэффициент дружбы с вами. Лексикографическое сравнение реализует оператор "<" в современных языках программирования. Строка a лексикографически меньше строки b, если либо a является префиксом b, либо существует такое i (1 ≤ i ≤ min(|a|, |b|)), что ai < bi, а для любого j (1 ≤ j < i) aj = bj, где |a| и |b| обозначают длины строк a и b соответственно. | |
![]()
|
|
F. Длинное число
математика
Разбор выражений
теория чисел
*3400
Рассмотрим следующую грамматику: - <expression> ::= <term> | <expression> '+' <term>
- <term> ::= <number> | <number> '-' <number> | <number> '(' <expression> ')'
- <number> ::= <pos_digit> | <number> <digit>
- <digit> ::= '0' | <pos_digit>
- <pos_digit> ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
Эта грамматика задаёт число в десятичной системе счисления по следующим правилам: - <number> задаёт себя,
- <number>-<number> (l-r, l ≤ r) задаёт число, полученное как конкатенация всех чисел от l до r, записанных без ведущих нулей. Например, 8-11 задает число 891011,
- <number>(<expression>) задаёт число, полученное как конкатенация <number> копий числа, задаваемого <expression>,
- <expression>+<term> задаёт число, полученное как конкатенация чисел, задаваемых <expression> и <term>.
Пример: 2(2-4+1)+2(2(17)) задаёт число 2341234117171717. Дано выражение, выведите остаток от деления числа, которое оно задаёт, на 109 + 7. Выходные данные В единственной строке выведите остаток от деления числа, задаваемого выражением, на 109 + 7. | |
![]()
|
|
B. Побитовая формула
битмаски
Перебор
поиск в глубину и подобное
Разбор выражений
реализация
*1800
Вася недавно прочитал о битовых операциях, которые используются в компьютерах: AND, OR и XOR. Он неплохо изучил их свойства и придумал новую игру. Изначально Вася выбирает разрядность m для своей игры, это значит, что все числа в игре будут состоять из m битов. Потом он просит Петю выбрать некоторое одно m-битное число. После этого Вася вычисляет значения n переменных. Каждой из переменных присваивается либо константное m-битное число, либо результат выполнения битовой операции, операндами которой могут являться уже определенные переменные или выбранное Петей число. После этого сумма очков, которую получает Петя, равна сумме значений всех переменных. Вася хочет узнать, какое число должен выбрать Петя, чтобы получить минимально возможное число очков, и какое число он должен выбрать, чтобы получить максимальное число очков. В обоих случаях, если у Пети есть несколько способов получить такую сумму, найдите минимальное число, которое он может выбрать. Выходные данные В первой строке выведите минимальное число, которое должен выбрать Петя, чтобы сумма значений всех переменных была минимальна, во второй строке — минимальное число, которое должен выбрать Петя, чтобы сумма значений всех переменных была максимальна. Оба числа выведите в виде двоичного m-битного числа. Примечание В первом тесте если Петя выбирает число 0112, то a = 1012, b = 0112, c = 0002, сумма их значений равна 8. Если же он выберет число 1002, то a = 1012, b = 0112, c = 1112, сумма их значений равна 15. Для второго теста минимальная и максимальная суммы переменных a, bb, cx, d и e равны 2 и не зависят от загаданного числа, поэтому минимальное число, которое может выбрать Петя — 0. | |
![]()
|
|
B. Библиотека виджетов
графы
дп
Разбор выражений
реализация
*2300
Вася пишет свою собственную библиотеку для построения графического пользовательского интерфейса. Свое детище Вася назвал VTK (VasyaToolKit). Одним из интересных аспектов данной библиотеки является упаковка виджетов друг в друга. Виджетом называется некоторый элемент графического интерфейса. Каждый виджет имеет ширину и высоту, и занимает некоторый прямоугольник на экране. В Васиной библиотеке любой виджет имеет тип Widget. Далее для простоты мы будем отождествлять виджет и его тип. Типы HBox и VBox — производные от типа Widget, поэтому тоже являются типами Widget. Виджеты HBox и VBox — особенные. Они могут хранить в себе другие виджеты. Оба эти виджета с помощью метода pack() могут вложить непосредственно в себя какой либо другой виджет. Виджеты типов HBox и VBox могут хранить в себе несколько других виджетов, в том числе несколько одинаковых — они просто будут отображены несколько раз. В результате выполнения метода pack() сохраняется только ссылка на вложенный виджет, то есть при изменении вложенного виджета, его изображение в виджете, в который он вложен, тоже изменится. Будем считать, что виджет a вложен в виджет b если существует цепочка виджетов a = c1, c2, ..., ck = b, k ≥ 2, для которых ci вложен непосредственно в ci + 1 для любого 1 ≤ i < k. В Васиной библиотеке не допускается ситуация, что виджет a вложен в виджет a (то есть в себя) — при попытке вложить виджеты друг в друга таким образом сразу же выдается ошибка. Также виджеты HBox и VBox имеют параметры border и spacing, которые задаются методами set_border() и set_spacing() соответственно. По умолчанию оба этих параметра равны 0.  На картинке выше видно каким образом виджеты упаковываются в HBox и VBox. При этом HBox и VBox автоматически меняют свой размер в зависимости от размеров вложенных виджетов. Сами HBox и VBox отличаются только тем, что в HBox виджеты упаковываются по горизонтали, а в VBox — по вертикали. При этом параметр spacing задает расстояние между соседними виджетами, а border — рамку вокруг всех вложенных виджетов нужной ширины. Вложенные виджеты располагаются ровно в том порядке, в котором для них был вызван метод pack(). Если внутри HBox или VBox нет ни одного вложенного виджета, то их размеры равны 0 × 0 вне зависимости от параметров border и spacing. Построение всех виджетов идет с помощью скриптового языка VasyaScript. Описание этого языка вы найдете в описании входных данных. Для контрольной проверки верности своего кода Вася просит написать вас программу, вычисляющую размеры всех виджетов по исходному коду на языке VasyaScript. Выходные данные Для каждого виджета в отдельной строке выведите через пробел его название, ширину и высоту. Строки должны быть упорядочены лексикографически по названию виджета. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). Примечание В первом примере виджеты располагаются следующим образом:  | |
![]()
|
|
D1. Hyperspace Jump (easy)
математика
Разбор выражений
*1400
The Rebel fleet is on the run. It consists of m ships currently gathered around a single planet. Just a few seconds ago, the vastly more powerful Empire fleet has appeared in the same solar system, and the Rebels will need to escape into hyperspace. In order to spread the fleet, the captain of each ship has independently come up with the coordinate to which that ship will jump. In the obsolete navigation system used by the Rebels, this coordinate is given as the value of an arithmetic expression of the form  . . To plan the future of the resistance movement, Princess Heidi needs to know, for each ship, how many ships are going to end up at the same coordinate after the jump. You are her only hope! Output Print a single line consisting of m space-separated integers. The i-th integer should be equal to the number of ships whose coordinate is equal to that of the i-th ship (including the i-th ship itself). Note In the sample testcase, the second and the third ship will both end up at the coordinate 3. Note that this problem has only two versions – easy and hard. | |
![]()
|