| | | |
|
Организация коров фермера Джона
Двоичное дерево поиска
Организация коров фермера Джона (UCFJ) направляет делегацию на Международную олимпиаду по овцеводству (IOI).
N коров участвуют в выборе делегации (1≤N≤2⋅105). Они стоят в ряд, и корова i имеет породу bi.
Делегация состоит из непрерывного интервала как минимум двух коров - то есть из коров l…r для целых l и r удовлетворяющих 1≤l<r≤N. две внешние коровы выбранного интервала называются "лидерами". Чтобы избежать конфликта между породами коров каждый лидер должен иметь породу отличающуюся от остальных коров делегации (лидеров и не лидеров).
Определите количество способов выбрать делегацию.
Входные данные:
Первая строка содержит N.
Вторая строка содержит N целых чисел b1,b2,…,bN, каждое в интервале [1,N].
Выходные данные:
Количество возможных делегаций, на отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
7
1 2 3 4 3 2 5 |
13 |
Каждая делегация соответствует одной из следующих пар лидеров:
(1,2),(1,3),(1,4),(1,7),(2,3),(2,4),(3,4),(4,5),(4,6),(4,7),(5,6),(5,7),(6,7). |
| |
![]()
|
|
Коллайдер
Двоичное дерево поиска
Задачи на моделирование
Физики проводят эксперимент для исследования частиц трёх типов: x, y и z. Они запускают в коллайдер пронумерованный ряд из n частиц. Во время эксперимента происходит воздействие на одну конкретную частицу, после чего частица исчезает с i-ого места ряда и моментально появляется на месте j. После её исчезновения номера частиц, стоящих правее, уменьшаются на 1, а после появления, номера частиц, стоящих правее, увеличиваются на 1. После определенного числа воздействий физики интересуются какая частица стоит на месте k. Напишите программу, которая поможет физикам.
Входные данные
В первой строке файла два целых числа: n – количество частиц и m — общее количество воздействий и вопросов (1 ≤ n ≤ 1000000, 1 ≤ m ≤ 15000). Во второй строке — последовательность из символов x, y и z длиной n. На каждой из следующих m строк (1 ≤ m ≤ 15000) описано воздействие или вопрос. Строка, в которой описано воздействие, начинается символом a и после пробела дается два целых числа из интервала [1; n]. Первое из них показывает начальное, а второе - конечное местоположение частицы во время воздействия. Строка, в которой описан вопрос, начинается символом q и после пробела дается одно целое число из интервала [1; n]. Оно указывает позицию, которая интересует физиков.
Выходные данные
Выведите столько строк, сколько вопросов во входном файле. В строке номер i надо записать ответ на вопрос i — название соответствующей частицы x, y или z.
Пояснения к примеру
Последовательность после первого воздействия – xxyyzxxzxzyyzyx, последовательность после второго воздействия – xxyxyzxxzxzyyzy, последовательность после третьего воздействия – xyxyxyzxxzxzyzy,
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
15 6
xzxyyzxxzxyyzyx
a 2 10
a 15 4
q 3
a 12 2
q 14
q 2 |
y
z
y |
| |
![]()
|
|
Река
Структуры данных
Двоичное дерево поиска
Двоичное дерево поиска
Двоичное дерево поиска
Корневая оптимизация
Декартово дерево
Во Флатландии протекает богатая рыбой река Большой Флат. Много лет назад река была поделена между n рыболовными предприятиями, каждое из которых получило непрерывный отрезок реки. При этом i-е предприятие, если рассматривать их по порядку, начиная от истока, изначально получило отрезок реки длиной ai .
С тех пор с рыболовными предприятиями во Флатландии k раз происходили различные события. Каждое из событий было одного из двух типов: банкротство некоторого предприятия или разделение некоторого предприятия на два.
При некоторых событиях отрезок реки, принадлежащий предприятию, с которым это событие происходит, делится на две части. Каждый такой отрезок имеет длину большую или равную 2. Деление происходит по следующему правилу. Если отрезок имеет четную длину, то он делится на две равные части. Иначе он делится на две части, длины которых различаются ровно на единицу, при этом часть, которая ближе к истоку реки, имеет меньшую длину.
При банкротстве предприятия происходит следующее. Отрезок реки, принадлежавший обанкротившемуся предприятию, переходит к его соседям. Если у обанкротившегося предприятия один сосед, то этому соседу целиком передается отрезок реки обанкротившегося предприятия. Если же соседей двое, то отрезок реки делится на две части описанным выше способом, после чего каждый из соседей присоединяет к своему отрезку ближайшую к нему часть.
При разделении предприятия отрезок реки, принадлежавший разделяемому предприятию, всегда делится на две части описанным выше способом. Разделившееся предприятие ликвидируется, и образуются два новых предприятия. Таким образом, после каждого события каждое предприятие владеет некоторым отрезком реки.
Министерство финансов Флатландии предлагает ввести налог на рыболовные предприятия, пропорциональный квадрату длины отрезка реки, принадлежащего соответствующему предприятию. Чтобы проанализировать, как будет работать этот налог, министр хочет по имеющимся данным узнать, как изменялась величина, равная сумме квадратов длин отрезков реки, принадлежащих предприятиям, после каждого произошедшего события.
Требуется написать программу, которая по заданному начальному разделению реки между предприятиями и списку событий, происходивших с предприятиями, определит, чему равна сумма квадратов длин отрезков реки, принадлежащих предприятиям, в начальный момент времени и после каждого события.
Формат входного файла
Первая строка входного файла содержит два целых числа: n и p — исходное количество предприятий (2 ≤ n ≤ 100 000) и номер подзадачи (0 ≤ p ≤ 4). Вторая строка входного файла содержит n целых чисел a1, a2, …, an — длины исходных отрезков реки. Третья строка входного файла содержит целое число k — количество событий, происходивших с предприятиями (1 ≤ k ≤ 100 000). Последующие k строк содержат описания событий, i-я строка содержит два целых числа: ei и vi — тип события и номер предприятия, с которым оно произошло. Значение ei = 1 означает, что предприятие, которое после всех предыдущих событий является vi-м по порядку, если считать с единицы от истока реки, обанкротилось, а значение ei = 2 означает, что это предприятие разделилось на два. Гарантируется, что значение vi не превышает текущее количество предприятий. Гарантируется, что если отрезок предприятия при банкротстве или разделении требуется поделить на две части, то он имеет длину большую или равную 2. Гарантируется, что если на реке осталось единственное предприятие, оно не банкротится.
Формат выходного файла
Выходной файл должен содержать (k + 1) целых чисел, по одному в строке. Первая строка должна содержать исходную сумму квадратов длин отрезков реки, а каждая из последующих k строк — сумму квадратов длин отрезков реки после очередного события.
Пример
Ввод:
4 0
3 5 5 4
5
1 1
2 1
1 3
2 2
1 3
Вывод:
75
105
73
101
83
113
Пояснение к примеру
Распределение отрезков реки между предприятиями после каждого события, описанного в примере, приведено на рисунке ниже.
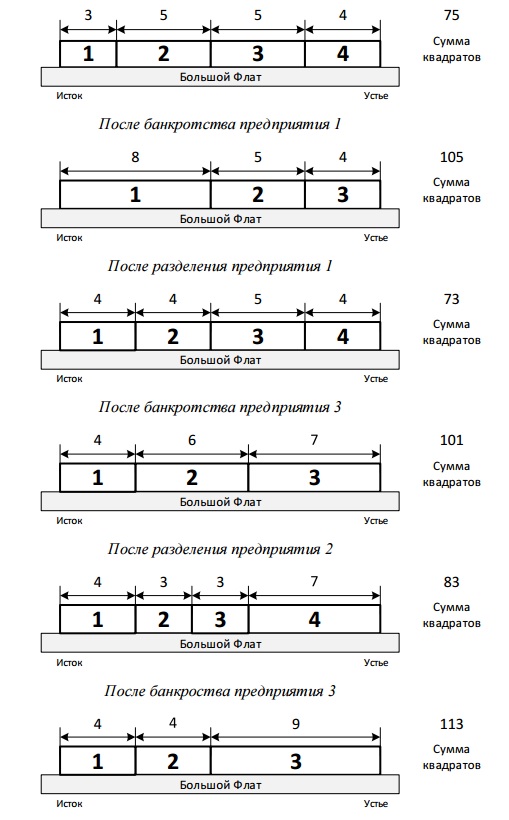
| |
![]()
|
|
Река
Структуры данных
Двоичное дерево поиска
Двоичное дерево поиска
Двоичное дерево поиска
Корневая оптимизация
Декартово дерево
Во Флатландии протекает богатая рыбой река Большой Флат. Много лет назад река была поделена между n рыболовными предприятиями, каждое из которых получило непрерывный отрезок реки. При этом i-е предприятие, если рассматривать их по порядку, начиная от истока, изначально получило отрезок реки длиной ai .
С тех пор с рыболовными предприятиями во Флатландии k раз происходили различные события. Каждое из событий было одного из двух типов: банкротство некоторого предприятия или разделение некоторого предприятия на два.
При некоторых событиях отрезок реки, принадлежащий предприятию, с которым это событие происходит, делится на две части. Каждый такой отрезок имеет длину большую или равную 2. Деление происходит по следующему правилу. Если отрезок имеет четную длину, то он делится на две равные части. Иначе он делится на две части, длины которых различаются ровно на единицу, при этом часть, которая ближе к истоку реки, имеет меньшую длину.
При банкротстве предприятия происходит следующее. Отрезок реки, принадлежавший обанкротившемуся предприятию, переходит к его соседям. Если у обанкротившегося предприятия один сосед, то этому соседу целиком передается отрезок реки обанкротившегося предприятия. Если же соседей двое, то отрезок реки делится на две части описанным выше способом, после чего каждый из соседей присоединяет к своему отрезку ближайшую к нему часть.
При разделении предприятия отрезок реки, принадлежавший разделяемому предприятию, всегда делится на две части описанным выше способом. Разделившееся предприятие ликвидируется, и образуются два новых предприятия. Таким образом, после каждого события каждое предприятие владеет некоторым отрезком реки.
Министерство финансов Флатландии предлагает ввести налог на рыболовные предприятия, пропорциональный квадрату длины отрезка реки, принадлежащего соответствующему предприятию. Чтобы проанализировать, как будет работать этот налог, министр хочет по имеющимся данным узнать, как изменялась величина, равная сумме квадратов длин отрезков реки, принадлежащих предприятиям, после каждого произошедшего события.
Требуется написать программу, которая по заданному начальному разделению реки между предприятиями и списку событий, происходивших с предприятиями, определит, чему равна сумма квадратов длин отрезков реки, принадлежащих предприятиям, в начальный момент времени и после каждого события.
Формат входного файла
Первая строка входного файла содержит два целых числа: n и p — исходное количество предприятий (2 ≤ n ≤ 100 000) и номер подзадачи (0 ≤ p ≤ 4). Вторая строка входного файла содержит n целых чисел a1, a2, …, an — длины исходных отрезков реки. Третья строка входного файла содержит целое число k — количество событий, происходивших с предприятиями (1 ≤ k ≤ 100 000). Последующие k строк содержат описания событий, i-я строка содержит два целых числа: ei и vi — тип события и номер предприятия, с которым оно произошло. Значение ei = 1 означает, что предприятие, которое после всех предыдущих событий является vi-м по порядку, если считать с единицы от истока реки, обанкротилось, а значение ei = 2 означает, что это предприятие разделилось на два. Гарантируется, что значение vi не превышает текущее количество предприятий. Гарантируется, что если отрезок предприятия при банкротстве или разделении требуется поделить на две части, то он имеет длину большую или равную 2. Гарантируется, что если на реке осталось единственное предприятие, оно не банкротится.
Формат выходного файла
Выходной файл должен содержать (k + 1) целых чисел, по одному в строке. Первая строка должна содержать исходную сумму квадратов длин отрезков реки, а каждая из последующих k строк — сумму квадратов длин отрезков реки после очередного события.
Пример
Ввод:
4 0
3 5 5 4
5
1 1
2 1
1 3
2 2
1 3
Вывод:
75
105
73
101
83
113
Пояснение к примеру
Распределение отрезков реки между предприятиями после каждого события, описанного в примере, приведено на рисунке ниже.

| |
![]()
|
|
Река
Структуры данных
Двоичное дерево поиска
Двоичное дерево поиска
Двоичное дерево поиска
Корневая оптимизация
Декартово дерево
Во Флатландии протекает богатая рыбой река Большой Флат. Много лет назад река была поделена между n рыболовными предприятиями, каждое из которых получило непрерывный отрезок реки. При этом i-е предприятие, если рассматривать их по порядку, начиная от истока, изначально получило отрезок реки длиной ai .
С тех пор с рыболовными предприятиями во Флатландии k раз происходили различные события. Каждое из событий было одного из двух типов: банкротство некоторого предприятия или разделение некоторого предприятия на два.
При некоторых событиях отрезок реки, принадлежащий предприятию, с которым это событие происходит, делится на две части. Каждый такой отрезок имеет длину большую или равную 2. Деление происходит по следующему правилу. Если отрезок имеет четную длину, то он делится на две равные части. Иначе он делится на две части, длины которых различаются ровно на единицу, при этом часть, которая ближе к истоку реки, имеет меньшую длину.
При банкротстве предприятия происходит следующее. Отрезок реки, принадлежавший обанкротившемуся предприятию, переходит к его соседям. Если у обанкротившегося предприятия один сосед, то этому соседу целиком передается отрезок реки обанкротившегося предприятия. Если же соседей двое, то отрезок реки делится на две части описанным выше способом, после чего каждый из соседей присоединяет к своему отрезку ближайшую к нему часть.
При разделении предприятия отрезок реки, принадлежавший разделяемому предприятию, всегда делится на две части описанным выше способом. Разделившееся предприятие ликвидируется, и образуются два новых предприятия. Таким образом, после каждого события каждое предприятие владеет некоторым отрезком реки.
Министерство финансов Флатландии предлагает ввести налог на рыболовные предприятия, пропорциональный квадрату длины отрезка реки, принадлежащего соответствующему предприятию. Чтобы проанализировать, как будет работать этот налог, министр хочет по имеющимся данным узнать, как изменялась величина, равная сумме квадратов длин отрезков реки, принадлежащих предприятиям, после каждого произошедшего события.
Требуется написать программу, которая по заданному начальному разделению реки между предприятиями и списку событий, происходивших с предприятиями, определит, чему равна сумма квадратов длин отрезков реки, принадлежащих предприятиям, в начальный момент времени и после каждого события.
Формат входного файла
Первая строка входного файла содержит два целых числа: n и p — исходное количество предприятий (2 ≤ n ≤ 100 000) и номер подзадачи (0 ≤ p ≤ 4). Вторая строка входного файла содержит n целых чисел a1, a2, …, an — длины исходных отрезков реки. Третья строка входного файла содержит целое число k — количество событий, происходивших с предприятиями (1 ≤ k ≤ 100 000). Последующие k строк содержат описания событий, i-я строка содержит два целых числа: ei и vi — тип события и номер предприятия, с которым оно произошло. Значение ei = 1 означает, что предприятие, которое после всех предыдущих событий является vi-м по порядку, если считать с единицы от истока реки, обанкротилось, а значение ei = 2 означает, что это предприятие разделилось на два. Гарантируется, что значение vi не превышает текущее количество предприятий. Гарантируется, что если отрезок предприятия при банкротстве или разделении требуется поделить на две части, то он имеет длину большую или равную 2. Гарантируется, что если на реке осталось единственное предприятие, оно не банкротится.
Формат выходного файла
Выходной файл должен содержать (k + 1) целых чисел, по одному в строке. Первая строка должна содержать исходную сумму квадратов длин отрезков реки, а каждая из последующих k строк — сумму квадратов длин отрезков реки после очередного события.
Пример
Ввод:
4 0
3 5 5 4
5
1 1
2 1
1 3
2 2
1 3
Вывод:
75
105
73
101
83
113
Пояснение к примеру
Распределение отрезков реки между предприятиями после каждого события, описанного в примере, приведено на рисунке ниже.

| |
![]()
|
|
Высота дерева
Деревья
Двоичное дерево поиска
Реализуйте бинарное дерево поиска для целых чисел. Программа получает на вход последовательность целых чисел и строит из них дерево. Элементы в деревья добавляются в соответствии с результатом поиска их места. Если элемент уже существует в дереве, добавлять его не надо. Балансировка дерева не производится.
Входные данные
На вход программа получает последовательность натуральных чисел. Последовательность завершается числом 0, которое означает конец ввода, и добавлять его в дерево не надо.
Выходные данные
Выведите единственное число – высоту получившегося дерева.
Пример соответствует следующему дереву:
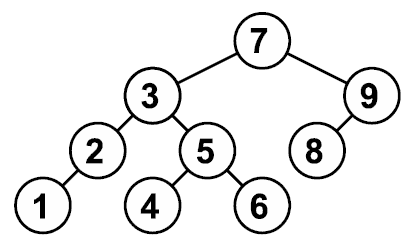
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
4
|
| |
![]()
|
|
Количество элементов в дереве
Деревья
Двоичное дерево поиска
Подсчитайте количество элементов в получившемся дереве и выведите это количество.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
9
|
| |
![]()
|
|
Второй максимум в дереве
Деревья
Двоичное дерево поиска
Выведите второй по величине элемент в построенном дереве. Гарантируется, что такой найдется.
Входные данные
Дана последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
8
|
| |
![]()
|
|
Обход дерева
Деревья
Двоичное дерево поиска
Выведите все элементы полученного дерева в порядке возрастания.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит. По данной последовательности требуется построить дерево.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
1
2
3
4
5
6
7
8
9
|
| |
![]()
|
|
Выведи листья
Деревья
Двоичное дерево поиска
Для полученного дерева выведите список всех листьев (вершин, не имеющих потомков) в порядке возрастания.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
1
4
6
8
|
| |
![]()
|
|
Выведи развилки
Деревья
Двоичное дерево поиска
Для полученного дерева выведите список всех вершин, имеющих по два ребёнка, в порядке возрастания.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит. Постройте по этой последовательности дерево.
Выходные данные
Выведите ответ задачи.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
3
5
7
|
| |
![]()
|
|
Ветки дерева
Деревья
Двоичное дерево поиска
Для полученного дерева выведите список всех вершин, имеющих только одного ребёнка, в порядке возрастания.
Входные данные
Вводится последовательность целых чисел,оканчивающаяся нулем. Построить по ней дерево.
Выходные данные
Выведите список требуемых вершин.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
2
9
|
| |
![]()
|
|
Сбалансированность
Деревья
Двоичное дерево поиска
Дерево называется сбалансированным, если для любой его вершины высота левого и правого поддерева для этой вершины различаются не более чем на 1.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит. Постройте дерево, соответствующее данной последовательности.
Выходные данные
Определите, является ли дерево сбалансированным, выведите слово YES или NO.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
YES
|
| |
![]()
|
|
Частоты появления элементов дерева
Двоичное дерево поиска
По данной последовательности постройте дерево, запоминая для каждого элемента его значение и количество его повторений в последовательности.
Входные данные
Вводится последовательность целых чисел, заканчивающаяся нулем. Сам ноль в последовательность не входит.
Выходные данные
Выведите на экран содержимое дерева в порядке возрастания, по одному элементу на строку. В каждой строке выводите значение элемента, затем, через пробел, укажите, сколько раз он встречается в исходной последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
1 1
2 1
3 1
4 1
5 1
6 1
7 1
8 1
9 1
|
| |
![]()
|
|
База данных
Двоичное дерево поиска
Ценные бумаги на фондовом рынке характеризуются множеством параметров. У них есть цена и ликвидность, также оценивать динамичность изменения цены, среднюю прибыльность, потенциал роста прибыльности и др. показатели. Аналитики трейдовой компании "WebMarket" ввели специальный показатель надежности ценной бумаги и научились эффективно его оценивать. Большое значение этого показателя соответствует малому риску покупки ценной бумаги. Но с ростом надежности обычно падает среднее оцениваемое значение прибыльности.
Для своих клиентов, играющих на рынке ценных бумаг, компания "WebMarket" решила открыть значения этого показателя и более того, автоматизировать покупку ценных бумаг с заданным порядковым номером по значению надежности. Аналитики проанализировали идею, и решили, что наличие такого функционала будет способствовать привлечению новых клиентов на рынок "WebMarket", повышению объемов сделок, а значит, и повышению прибылей "WebMarket". Важно также отметить, что торговля на базе этого показателя может позитивно сказаться на российском фондовом рынке и cделать его более здоровым. Алгоритмы оценки надежности уже написаны, средства выделены, необходимая реклама проведена. Осталось только написать сам код.
Ценные бумаги в базе данных имеют три атрибута:
- code — непустая строка латинских символов и цифр длины 30 или меньше
- id — целочисленный идентификатор (начиная с 0)
- reliability — целое число из диапазона [−231,231)
.
Каждой новой ЦБ выдается следующий по порядку id и значение её надёжности устанавливается в 0. Если ценная бумага отзывается с рынка, ее id для новых бумаг не используется.
База данных получает запросы, которые позволяют вводить новые ЦБ на рынок, получать текущую информацию о ЦБ, отзывать ЦБ с рынка, менять значение надежности у ЦБ и находить ЦБ, которая стоит на n-м месте, если упорядочить ЦБ по убыванию надежности, а при одинаковых значениях по возрастанию идентификатора.
При добавлении ЦБ с кодом, который раньше встречался, но соответствующая ЦБ была отозвана с рынка, ей назначается новый идентификатор.
Входные данные
Первая строка входа содержит число запросов N. (1≤N≤100000). Затем идут N строк, каждая из которых содержит один запрос. Запросы бывают 4 типов:
- ISSUE code: добавить новую ЦБ code в базу данных, или вывести информацию о ЦБ, если она уже есть в базе
- если ЦБ code существует, то вывести EXISTS id reliability
- если ЦБ code не существует, то вывести CREATED id 0
- DELETE code: удалить ЦБ code из базы
- если ЦБ code существует, то вывести OK id reliability
- если ЦБ code не существует, то вывести BAD REQUEST
- RELIABILITY code reliability: увеличить количество очков ЦБ, гарантируется, что значение останется в диапазоне [−231,231)
- если ЦБ code существует, то вывести OK id new_reliability
- если ЦБ code не существует, то вывести BAD REQUEST
- FIND n: найти n-ю ЦБ (начиная с 0)
- если база не пуста, найти ЦБ, которая имела бы порядковый номер n (нумерация начинается с 0), если все ЦБ упорядочить сначала по убыванию баллов, а группы ЦБ с одинаковыми баллами упорядочить по времени их добавления (то есть по возрастанию id); а если n больше, чем количество ЦБ в базе, то найти последнюю ЦБ в этом порядке; для обоих случаев вывести OK code id reliability
- если база пуста, то вывести EMPTY
Выходные данные
Таким образом, на каждый запрос на входе нужно вывести одну строку с результатом.
| |
![]()
|
|
Экзамены
Жадный алгоритм
Двоичное дерево поиска
Теория расписаний
Первая сессия обычно доставляет много проблем. Одна из них заключается в том, что студенту нужен по крайней мере целый день, чтобы подготовиться к одному экзамену. В день одного экзамена к другому готовиться невозможно. Но основная проблема заключается в том, что студенты могут начать готовиться к i-му экзамену, не раньше чем за ti дней до него, иначе они все забудут. Глеб хочет начать готовиться к экзаменам как можно позже, но он собирается все экзамены сдать.
Помогите Глебу выбрать день начала подготовки к экзаменам.
Входные данные
Первая строка выходных данных содержит число экзаменов n (1 ≤ n ≤ 50 000). Следующие строки описывают экзамены. Каждое описание состоит из трех строк. Первая строка – это название экзамена (строка, содержащая только латинские буквы, длиной не более 10). Вторая строка – дата экзамена в формате dd.mm.yyyy. Третья строка содержит величину ti для этого экзамена (1 ≤ ti ≤ 100 000). Все экзамены проходят от 01.01.1900 до 31.12.2100. Не забудьте, что високосными считаются годы, которые делятся на 4 и не делятся на 100 или которые делятся на 400.
Выходные данные
Выведите в формате dd.mm.yyyy, когда Глеб самое позднее сможет приступить к подготовке к экзаменам. Если расписание не позволяет подготовиться к каждому из экзаменов, то выведите слово Impossible.
| |
![]()
|