| | | |
|
Чет-нечет
Бинарный поиск по ответу
"Длинная" арифметика
Дана возрастающая последовательность целых чисел 1, 2, 4, 5, 7, 9, 10, 12, 14, 16, 17, ... Она сформирована следующим образом: берется одно нечетное число, затем два четных, затем три нечетных и так далее. Выведите N-й элемент этой последовательности.
Входные данные
Одно целое число N (1 ≤ N ≤ 10100).
Выходные данные
Выведите одно целое число - N-й элемент последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
| 2 |
4 |
5 |
| |
![]()
|
|
COWBASIC
"Длинная" арифметика
Задача на реализацию
Беси изобрела новый язык программирования, но поскольку нет компилятора, она нуждается в Вашей помощи для исполнения её программ.
COWBASIC - это простой, элегантный язык. У него две основные черты: сложение и циклы. Для решения проблемы переполнения, Беси выполняет все операции сложения по модулю 109+7. MOO-цикл исполняет блок кода фиксированное количество раз. Циклы и сложения могут быть вложенными.
Вам дана COWBASIC-программа, определите результат её выполнения - число, которое она вернёт.
ФОРМАТ ВВОДА:
Вам дана COWBASIC-программа длиной не более 100 строк, каждая строка длиной не более 350 символов. COWBASIC-программа это список операторов.
Имеется три типа операторов:
<переменная> = <выражение>
<литерал> MOO {
<список операторов>
}
RETURN <переменная>
Имеется три типа выражений:
<литерал>
<перменная>
( <выражение> ) + ( <выражение> )
Литерал - это положительное целое число не более 100,000.
Переменная - это строка не более 10 маленьких латинских букв.
Гарантируется, что переменная никогда не будет использована или возвращена оператором RETURN прежде, чем она будет определена. Гарантируется, оператор RETURN будет только один раз в последней строке программы.
ФОРМАТ ВЫВОДА:
Выведите одно положительное целое число - значение переменной, возвращённой оператором RETURN.
ОЦЕНИВАНИЕ
в 20% тестов MOO-циклы не вложены.
В других 20% всех тестов программу будет иметь только одну переменную. MOO-циклы могут быть вложенными
В остальных тестах нет никаких ограничений.
| Ввод |
Вывод |
Примечание |
x = 1
10 MOO {
x = ( x ) + ( x )
}
RETURN x
|
1024 |
Эта COWBASIC-программа вычисляет 210 |
n = 1
nsq = 1
100000 MOO {
100000 MOO {
nsq = ( nsq ) + ( ( n ) + ( ( n ) + ( 1 ) ) )
n = ( n ) + ( 1 )
}
}
RETURN nsq
|
4761 |
Эта программа вычисляет (105∗105+1)2 (по модулю 109+7). |
| |
![]()
|
|
Красно-черные деревья
"Длинная" арифметика
Динамическое программирование на графах
Широкое распространение в стандартных библиотеках многих языков программирования получила реализация сбалансированных деревьев на основе так называемых красно-черных деревьев. В данной задаче вам предлагается посчитать количество красно-черных деревьев заданной формы.
Напомним, что двоичным деревом называется набор вершин, организованных в виде дерева. Каждая вершина имеет не более двух детей, один из которых называется левым, а другой — правым. Как левый, так и правый ребенок, а также оба могут отсутствовать.
Если вершина \(Y\) — ребенок вершины \(X\), то говорят, что вершина \(X\) является родителем вершины \(Y\). У каждой вершины дерева, кроме одной, есть ровно один родитель. Единственная вершина, не имеющая родителя, называется корнем дерева.
Соединим каждую вершину кроме корня с ее родителем. Заметим, что для каждой вершины существует ровно один путь, ведущий в нее от корня.
Двоичное дерево называется красно-черным, если каждая его вершина раскрашена в красный либо в черный цвет, причем выполняются следующие условия:
-
если вершина красная, то ее родитель — черный;
-
количество черных вершин на пути от корня до любой вершины, у которой отсутствует хотя бы один ребенок, одно и то же.
Примеры двоичного дерева, вершины которого раскрашены в два цвета, приведены на следующем рисунке.
Если считать закрашенные вершины черными, а незакрашенные — красными, то дерево на рисунке (а) является красно-черным деревом, а деревья на рисунках (б) и (в) — нет. Для дерева на рисунке (б) нарушается первое свойство — у красной вершины 5 родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство — на пути от корня до вершины 1 одна черная вершина, а, например, на пути от корня до вершины 3 — две.
Для заданного двоичного дерева подсчитайте число способов раскрасить его вершины в черный и красный цвет так, чтобы оно стало красно-черным деревом.
Формат входных данных
Первая строка содержит число \(n\) — количество вершин в дереве (\(1 \le n \le 1000\)).
Пусть вершины дерева пронумерованы числами от \(1\) до \(n\). Следующие \(n\) строк содержат по два числа — для каждой вершины заданы номера ее левого и правого ребенка. Если один из детей отсутствует, то вместо его номера записан ноль. Гарантируется, что входные данные корректны, то есть набор чисел действительно задает двоичное дерево.
Формат выходных данных
Выведите одно число — количество способов раскрасить вершины заданного во входном файле двоичного дерева в красный и черный цвета так, чтобы оно стало красно-черным деревом.
Все допустимые способы раскрасить вершины дерева из первого примера приведены на следующем рисунке.
| |
![]()
|
|
Степень
"Длинная" арифметика
Для натуральных чисел a и n вычислить an.
Входные данные
В первой строке находятся разделённые пробелом a и n. 1 <= a <= 9, 1 <= n <= 7000.
Выходные данные
Выводится одно число - результат без стоящих впереди нулей, стоящих впереди и позади пробелов.
| |
![]()
|
|
Длинная сумма
"Длинная" арифметика
Даны два целых неотрицательных числа: M и N. Найти их сумму.
Входные данные
В первой строке содержится M, во второй - N. 0 <= M, N < 1030000.
Выходные данные
В первой строке вывести сумму без пробелов и ведущих нулей.
| |
![]()
|
|
Длинное произведение
"Длинная" арифметика
Даны целые неотрицательные числа M и N. Найти M*N.
Входные данные
В первой строке находится число M, во второй - N. 0 <= M, N <= 102500.
Выходные данные
Вывести одно число - результат умножения.
| |
![]()
|
|
Деление длинного числа на короткое
"Длинная" арифметика
Даны целое неотрицательное число M и целое положительное число N. Найти M div N и M mod N.
Входные данные
В первой строке находится число M, во второй - N. 0 <= M <= 1060000, 1 <= N <= 1 000 000.
Выходные данные
В первой строке вывести значение выражения M div N во второй - выражения M mod N.
| |
![]()
|
|
Системы счисления
"Длинная" арифметика
Дано целое неотрицательное число в I-ричной системе счисления. Вывести это число в J-ричной системе счисления.
Входные данные
В первой строке находятся числа I и J (в десятичной системе счисления), во второй строке - число для перевода. 2 <= I, J <= 36, для представления цифр 10...35 используются прописные латинские буквы A...Z
соответственно, число разрядов исходного числа не превышает 1000.
Выходные данные
Вывести искомое число. Если число начинается с буквы, перед ней не должно быть нуля.
| |
![]()
|
|
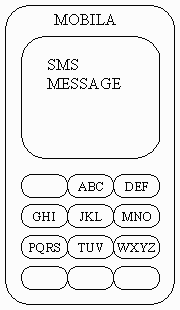
SMS
Динамическое программирование: два параметра
"Длинная" арифметика
Сообщения SMS сотового телефона MOBILA составлены из прописных латинских букв. Если буква первая на кнопке, нужно нажать эту кнопку один раз, чтобы добавить букву в сообщение. Если буква вторая - нужно нажать кнопку дважды и т.д. Так, чтобы набрать слово "SMS", нужно нажать
(PQRS)(PQRS)(PQRS)(PQRS)(MNO)(PQRS)(PQRS)(PQRS)(PQRS)
Чтобы ввести две буквы, находящиеся на одной кнопке, нужно между нажатиями клавиши сделать паузу. Например, чтобы ввести сообщение "AA", нужно нажать
(ABC)(пауза)(ABC)
Если на кнопке три буквы, то, как только такая кнопка нажата три раза, последняя буква добавляется в сообщение немедленно, а следующие нажатия той же кнопки относятся к следующей букве сообщения. Аналогично, если на кнопке четыре буквы, то после четырёх нажатий в сообщение будет добавлена последняя буква. То есть последовательность нажатий
(ABC)(ABC)(ABC)(ABC)(пауза)(ABC)
соответствует сообщению "CAA". К сожалению, сотовые телефоны этой модели давно не производятся, и остался только один такой телефон. Он может произвольно вставлять и игнорировать паузы во время ввода сообщения, что может привести к некоторым изменениям в сообщениях. Например, введя MOSCOWQUARTERFINAL, можно получить вместо этого OMSCMNWQTTARTERPDEINAL. Вы получили SMS-сообщение и знаете, что оригинальное сообщение содержало N букв. Чтобы определить вероятность угадывания оригинального сообщения, найдите число возможных сообщений, которые могли превратиться в то, которое Вы получили.
Входные данные
В первой строке задана длина оригинального сообщения N. Вторая строка содержит полученное SMS-сообщение. 1 <= N <= 80, полученное сообщение состоит только из прописных латинских букв, длина полученного сообщения - от 1 до 80 букв.
Выходные данные
Вывести число сообщений из N букв, которые, будучи набранными на на этом телефоне, могут превратиться в данное сообщение.
| |
![]()
|
|
Остаток от деления на цифру
"Длинная" арифметика
Напишите программу, вычисляющую остаток от деления заданного «длинного» числа на заданную цифру.
Входные данные
В первой строке задана цифра K (1≤K≤9). Во второй строке задано натуральное число N, состоящее из не более чем 100000 цифр.
Выходные данные
Выведите остаток от деления N на K.
| |
![]()
|
|
Остаток от деления на цифру
"Длинная" арифметика
Напишите программу, вычисляющую остаток от деления заданного «длинного» числа на заданную цифру.
Входные данные
В первой строке задана цифра K (1≤K≤9). Во второй строке задано натуральное число N, состоящее из не более чем 250 цифр.
Выходные данные
Выведите остаток от деления N на K.
| |
![]()
|