| | | |
|
Бюрократия
Динамическое программирование на поддеревьях
Мирко стал генеральным директором крупной корпорации. В компании работает N человек, которые пронумерованы числами от 1 до N, причем сам Мирко имеет номер 1. У всех работников, кроме Мирко, есть начальник. Начальник может иметь несколько подчиненных, но не более одного своего начальника.
Когда Мирко получает задание от инвесторов, он передает его своему подчиненному с наименьшим номером. Этот подчиненный также передает его своему подчиненному с наименьшим номером, и так далее, пока задание не перейдет несчастливому работнику без подчиненных, который должен его выполнить.
Этот работник получает 1 монету, его начальник получает 2 монеты, начальник этого начальника получает 3 монеты, и так далее. Потом тот, кто на самом деле сделал работу, осознает, насколько эта капиталистическая система несправедлива, и увольняется с работы.
Мирко получает задания до тех пор, пока в корпорации не останется всего один сотрудник — сам Мирко. Тогда он выполняет это задание, получает 1 монету и уходит из корпорации.
Ему стало интересно, сколько всего монет получил каждый бывший сотрудник. Помогите ему с этим.
Входные данные:
Первая строка содержит одно натуральное число N (1 ≤ N ≤ 2·105) — число сотрудников компании. Следующая строка содержит N-1 чисел a2, a3, ... an (1 ≤ ai < i), ai — номер начальника i-го сотрудника.
Выходные данные:
Выведите N чисел, i-е число должно означать, сколько монет получил i-й сотрудник.
Примеры:
| Входные Данные |
Выходные данные |
3
1 1 |
5 1 1 |
5
1 2 2 4 |
13 8 1 3 1 |
Пояснения:
Далее приведено описание ко второму примеру.
Мирко отдает первое задание работнику 2, который передает его работнику 3, который выполняет задание. Таким образом, работник 3 получает одну монету, работник 2 — две монеты, а работник 1, сам Мирко, — три монеты. После этого работник 3 увольняется.
Мирко отдает второе задание работнику 2, который передает его работнику 4, который тут же передает задание работнику 5, который выполняет задание. После этого работник 5 получает одну монету, работник 4 — две монеты, работник 2 — три монеты, а Мирко — четыре монеты. Работник 5 увольняется.
После выполнения третьего задания работник 4 получает одну монету, работник 2 — две монеты, а Мирко — три монеты, после чего работник 4 увольняется.
После выполнения четвертого задания работник 2 получает одну монету, а Мирко — две монеты, после чего второй работник увольняется.
Наконец, пятое задание выполняет сам Мирко, получая за это одну монету, после чего процесс прекращается.
Суммарно Мирко получил 13 монет, работник 2 — 8 монет, работник 4 — 3 монеты, а работники 3 и 5 — одну монету.
| |
![]()
|
|
Максимальное паросочетание дерева
Динамическое программирование на поддеревьях
Вам дано дерево (связный ациклический неориентированный граф), состоящее из n вершин.
Найдите размер его максимального паросочетания (набор попарно несмежных ребер).
Входные данные:
В первой строке дано число n - количество вершин в дереве.
Далее идет n-1 строка, в каждой из которых дается по два числа ai и bi (1 <= ai, bi <= n) - ребра дерева.
Выходные данные:
Выведите одно число - размер максимального паросочетания данного дерева.
Примеры:
| Входные данные |
Выходные данные |
4
1 2
2 3
3 4 |
2 |
Пояснение:
В максимальное паросочетание данного дерева будут входить ребра 1-2 и 3-4.
| |
![]()
|
|
Эн и фестиваль пирогов
Динамическое программирование на поддеревьях
Сегодня в замке Эна проходит фестиваль пирогов, в котором участвуют n пекарен, каждая из которых имеет свой уникальный номер от 1 до n.
Некоторые пекарни соединены между собой двусторонними дорогами, но таким образом, что если из пекарни i можно дойти до пекарни j, то существует ровно один маршрут между ними.
Когда Эн ест пироги в i-й пекарне, то он получает Ai удовольствия. А если проходит по дороге между некоторыми пекарнями с номерами v и u, то вкусный аромат пирогов приносит Эну Cv,u удовольствия.
Эн не хочет появляться в каждой пекарне больше одного раза (в некоторые можно не заходить вообще), но при этом хочет получить от фестиваля максимально возможное удовольствие.
Он начнет в какой-либо из пекарен и далее будет переходить между ними только по существующим дорогам.
Помогите Эну определить максимально возможное удовольствие, которое он сможет получить.
Входные данные:
В первой строке дано число n (1 <= n <= 50000) - количество пекарен, и число k - количество существующих дорог между пекарнями.
Во второй строке дано n чисел Ai (0 <= Ai <= 10000) - удовольствие от пирогов i-й пекарне.
Далее следует k строк, в каждой по 3 числа v, u, C (1 <= v, u <= n; v ≠ u; 0 <= C <= 10000), означающие, что существует дорога между пекарнями с номерами v и u, и аромат на этой дороге приносит C удовольствия.
Выходные данные:
Выведите одно число - максимально возможное удовльствие.
Примеры:
| Входные данные |
Выходные данные |
2 1
1 1
1 2 1 |
3 |
8 7
1 5 4 6 10 1 2 2
1 2 1
2 3 10
2 4 1
4 5 1
4 6 2
6 7 2
6 8 3 |
37 |
Пояснения:
В первом примере нужно начать в 1-й пекарне (1 удовольствие), пройти по дороге между 1-й и 2-й пекарнями (1 удовольствие) и посетить 2-ю пекарню (1 удовольствие). Суммарное удовольствие - 1+1+1 = 3.
Во втором примере нужно начать в 5-й пекарне (10 удовольствия), пройти по дороге между 5-й и 4-й пекарнями (1 удовольствие), посетить 4-ю пекарню (6 удовольствия), пройти по дороге между 4-й и 2-й пекарнями (1 удовольствие), посетить 2-ю пекарню (5 удовольствия), пройти по дороге между 2-й и 3-й пекарнями (10 удовольствия), посетить 3-ю пекарню (4 удовольствия). Суммарное удовольствие - 10+1+6+1+5+10+4 = 37.
| |
![]()
|
|
Кайман и пельмешки
Динамическое программирование на поддеревьях
Кайману снится необычный сон, будто он попал в странный район города. Этот район можно представить как граф-дерево, где вершины - это перекрестки и ребра - двусторонние дороги, которые соединяют эти перекрестки. Всего перекрестков n и у каждого свой номер от 0 до n-1.
Но не все так плохо в этом сне, ведь на каждой дороге между перекрестками с номерами u и v есть Сu,v пельменей! Кайман очень любит пельмешки, поэтому хочет съесть как можно больше, но есть проблема - если он побывает в каком-либо перекрестке более чем k раз, то на него нападет злой пельменный монстр.
Хоть это и сон, но пельмешки на каждой дороге можно съесть только один раз, хотя ничего не мешает ходить по дорогам по несколько раз. Также Кайман не останавливается на дорогах. То есть, если он начнет переходить от одного перекрестка к другому, то он обязательно пройдет дорогу полностью до следующего перекрестка.
В начале сна Кайман находится на перекрестке с номером 0. Помогите ему определить, какое максимальное количество пельменей он сможет съесть, но так, чтобы на него не напал злой пельменный монстр.
Входные данные:
В первой строке следует два целых числа n и k (3 ≤ n ≤ 105; 1 ≤ k ≤ 105) — количество перекрестков и максимальное количество посещений каждого из перекрестков.
В следующих n - 1 строках следует по три целых числа u, v и Cu,v (0 ≤ u, v ≤ n - 1; 0 ≤ Cu,v ≤ 10000), означающих, что перекрестки с номерами u и v связаны дорогой, на которой Cu,v пельменей.
Гарантируется, что перекрестки и дороги формируют дерево.
Выходные данные:
Выведите одно целое число - максимальное количество пельменей, которое сможет съесть Кайман.
Примеры:
| Входные данные |
Выходные данные |
9 3
0 1 1
0 2 1
1 3 2
1 4 2
1 5 2
2 6 3
2 7 3
2 8 3 |
15 |
9 5
0 1 1
0 2 1
1 3 2
1 4 2
1 5 2
2 6 3
2 7 3
2 8 3 |
17 |
11 6
1 0 7932
2 1 1952
3 2 2227
4 0 9112
5 4 6067
6 0 6786
7 6 3883
8 4 7137
9 1 2796
10 5 6200 |
54092 |
Пояснение:
В первом примере нужно посетить перекрестки в следующем порядке: 0, 1, 5, 1, 3, 1, 0, 2, 6, 2, 7, 2, 8. Тогда он съест суммарно 1+2+2+1+3+3+3 = 15 пельменей.
Обратите внимание, что ни один перекресток не посещается более чем 3 раза.
| |
![]()
|
|
Красота фейерверка
Обход в глубину
Применение обхода в глубину
Динамическое программирование
Динамическое программирование
Динамическое программирование на поддеревьях
В лаборатории теоретической пиротехники изучают новые технологии организации
фейерверков. Фейерверк представляется как корневое дерево, а поскольку в мощном
фейерверке его элементы также взрываются, порождая новые фейерверки, то ученые вводят
операцию возведения корневого дерева в степень.
Корневое дерево содержит одну или несколько вершин. Одна из вершин выделена и
называется корнем дерева, для каждой из остальных вершин ровно одна другая вершина
является родителем. При этом от любой вершины можно добраться до корня,
последовательно переходя от вершины к ее родителю. Вершина, которая не является
родителем никакой другой вершины, называется листом. Если вершина x является
родителем вершины y, то вершина y является ребенком вершины x. Будем говорить, что
вершина и ее родитель соединены ребром.
На рис. 1 показан пример корневого дерева с корнем в вершине 1. Родителем вершин
2 и 3 является вершина 1, родителем вершины 4 является вершина 2. Вершины 2 и 3 — дети
вершины 1, а вершина 4 — ребенок вершины 2. Листьями являются вершины 3 и 4.
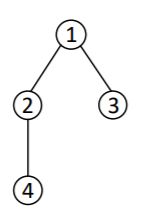
Рис. 1. Пример корневого дерева с корнем в вершине 1, листьями 3 и 4.
Фейерверк задается своим базовым деревом T и мощностью m. Фейерверк представляется деревом, которое получается в результате возведения дерева T в степень m. Операция возведения дерева в степень устроена следующим образом. Если m = 1, то результат T 1 — само дерево T. Для m > 1 рассмотрим дерево T m – 1 . Выполним следующую операцию: для каждого листа x дерева T m – 1 создадим копию дерева T и назначим лист x родителем корня соответствующей копии. Получившееся дерево будет деревом T m .
На рис. 2 показано дерево, представленное на рис. 1, в степенях 1, 2 и 3.
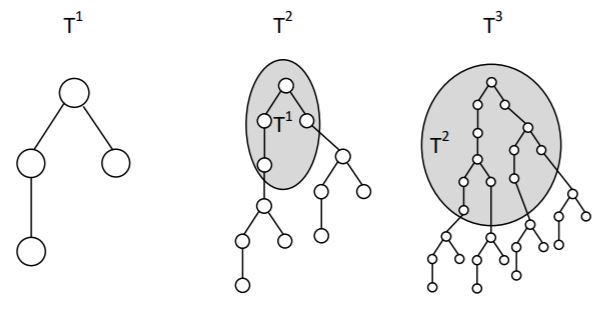
Рис. 2. Пример возведения дерева в степени 1, 2 и 3
Путем в дереве называется последовательность вершин, в которой две соседние
вершины соединены ребром. Все вершины в пути должны быть различны.
Для того, чтобы оценить красоту фейерверка, необходимо определить, какое
максимальное количество вершин может содержать путь в дереве, которым представляется
фейерверк. На рис. 3 приведен путь в дереве T2, содержащий максимальное количество
вершин. Таким образом, красота фейерверка с базовым деревом T и мощностью 2 равна 10.
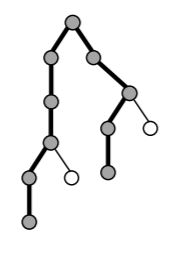
Рис. 3. Путь в дереве T 2 , содержащий максимальное количество вершин.
Требуется написать программу, которая по описанию дерева T и натуральному числу m определяет красоту фейерверка с базовым деревом T и мощностью m.
Формат входных данных
Первая строка входных данных содержит два натуральных числа n и m — количество
вершин в базовом дереве фейерверка T и его мощность (3 ≤ n ≤ 200 000, 1 ≤ m ≤ 200 000).
Вторая строка описывает дерево T и содержит (n – 1) целых чисел: p2, p3, …, pn —
номера родителей вершин 2, 3, …, n, соответственно (1 ≤ pi ≤ i – 1).
Формат выходных данных
Требуется вывести одно целое число — красоту фейерверка, представляемого
деревом Tm.
| |
![]()
|