| | | |
|
Самый длинный путь
Алгоритм Флойда
Дан ориентированный граф, рёбрам которого приписаны некоторые неотрицательные веса (длины). Надо найти две вершины, кратчайший путь между которыми имеет наибольшую длину.
Формат входных данных
В первой строке задано число вершин N ≤50. Далее идёт матрица смежности графа, то есть N строк, в каждой из которых записано N чисел. j-ое число в i-ой строке матрицы смежности задает длину ребра, ведущего из i-й вершину в j-ую. Длины могут принимать любые значения от от 0 до 1000000. Гарантируется, что на главной диагонали матрицы стоят нули.
Формат выходных данных
Выведите одно число – длину искомого пути.
| |
![]()
|
|
Есть ли цикл?
Обход в глубину
Алгоритм Флойда
Дан ориентированный граф. Требуется определить, есть ли в нем цикл.
Входные данные
В первой строке вводится число вершин N≤ 50. Далее в N строках следуют по N чисел, каждое из которых – 0 или 1. j-ое число в i-ой строке равно 1 тогда и только тогда, когда существует ребро, идущее из i-ой вершины в j-ую. Гарантируется, что на диагонали матрицы будут стоять нули.
Выходные данные
Выведите 0, если в заданном графе цикла нет, и 1, если он есть.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 1 0
0 0 1
0 0 0
|
0 |
| 2 |
3
0 1 0
0 0 1
1 0 0
|
1 |
| |
![]()
|
|
Отрицательный цикл-2
Алгоритм Флойда
Дан ориентированный граф. Определить, есть ли в нем цикл отрицательного веса, и если да, то вывести его.
Входные данные
В первой строке содержится число N (1 <= N <= 100) – количество вершин графа. В следующих N строках находится по N чисел – матрица смежности графа. Веса ребер по модулю меньше 100000. Если ребра нет, соответствующее значение равно 100000.
Выходные данные
В первой строке выведите "YES", если цикл существует, или "NO", в противном случае. При наличии цикла выведите во второй строке количество вершин в нем (считая одинаковые – первую и последнюю), а в третьей строке – вершины, входящие в этот цикл, в порядке обхода. Если циклов несколько, то выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
100000 100000 -51
100 100000 100000
100000 -50 100000
|
YES
4
3 2 1 3
|
| |
![]()
|
|
Кладоискатель
Алгоритм Флойда
Обход в ширину
Кладоискателю Васе попалась карта древнего подземелья. Подземелье представляет собой лабиринт размера N×M (1 ≤ N, M ≤ 100 , N×M ≤ 100). Каждая клетка лабиринта либо пуста и по ней можно пройти, либо содержит стену. Из клетки можно переходить только в смежную по стене клетку (так, у каждой клетки может быть не более 4 смежных).
В одной из клеток находится клад, который и хочет достать Вася. В лабиринте есть K входов, из которых Вася может начать свой путь.
Требуется определить, с какого входа Васе нужно начать свой путь, чтобы пройденное расстояние до клада было наименьшим. Если таких входов несколько, нужно вывести вход с наименьшим номером.
Входные данные
Первая строка содержит 2 числа N и M, задающие размеры лабиринта. Далее следует описание лабиринта: N строк по M символов в каждой. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с сокровищем (такая клетка в лабиринте ровно одна).
В (N+2)-й строке находится число K (1 ≤ K ≤ NxM) -- количество входов в лабиринт. Далее в K строках содержатся координаты входов. Так, в i-й строке содержатся числа xi и yi, означающие,что i-й вход расположен в xi-й строке и в yi-м столбце (1 ≤ xi ≤ N, 1 ≤ yi ≤ M). Гарантируется, что координаты входов попарно различны, и то, что все входы расположены в пустых клетках. Ни один из входов не находится в клетке с сокровищем.
Выходные данные
Необходимо вывести одно число - искомый номер входа (нумерация начинается с 1). Если до сокровища невозможно добраться, выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5
|
1 |
| 2 |
3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
|
-1 |
| |
![]()
|
|
Флойд - существование
Алгоритм Флойда
Дан ориентированный взвешенный граф. По его матрице смежности нужно для каждой пары вершин определить, существует ли кратчайший путь между ними или нет.
Комментарий: Кратчайший путь может не существовать по двум причинам:
- Нет ни одного пути
- Есть пути сколь угодно маленького веса
Входные данные
В первой строке входного файла записано единственное число: N (1 <=N <=100) — количество вершин графа. В следующих N строках по N чисел — матрица смежности графа (j-е число в i-й строке соответствует весу ребра из вершины i в вершину j): число 0 обозначает отсутствие ребра, а любое другое число — наличие ребра соответствующего веса. Все числа по модулю не превышают 100.
Выходные данные
Выведите N строк по N чисел. j-е число в i-й строке должно соответствовать кратчайшему пути из вершины i в вершину j. Число должно быть равно 0, если пути не существует, 1, если существует кратчайший путь, и 2, если пути существуют, но бывают пути сколь угодно маленького веса.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
0 1 2 0 0
1 0 3 0 0
2 3 0 0 0
0 0 0 0 -1
0 0 0 -1 0
|
1 1 1 0 0
1 1 1 0 0
1 1 1 0 0
0 0 0 2 2
0 0 0 2 2
|
| |
![]()
|
|
Космическое путешествие
Алгоритм Флойда
В MMORPG "Космические торговцы online" скорость перемещения игрока между звёздами ограничена одним парсеком в секунду. С такой скоростью можно быстро добраться до ближайших звёзд, но на путешествие с одного края галактики до другого может потребоваться несколько часов. Для ускорения таких долгих путешествий создатели игры сделали несколько "кротовых нор" — туннелей, соединяющих две точки в пространстве, которые позволяют мгновенно перемещаться между этими точками туда и обратно.
Напишите программу, которая вычисляет минимальное время путешествия, используя информацию о "кротовых норах".
В первой строке ввода содержится целое число N (1 ≤ N ≤ 100). Далее следует строка, содержащая 6 целых чисел — координаты начальной (xs,ys,zs) и конечной (xt,yt,zt) точки путешествия. Далее следует N строк, содержащих 6 целых чисел — координаты концов "кротовых нор". Все координаты измеряются в парсеках и находятся в диапазоне от 0 до 10000, и нет точек с совпадающими координатами.
Вывести минимальное время путешествия в секундах с точностью не менее 10 −6.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
0 0 0 100 100 0
1 1 1 50 100 10
|
52.722246 |
| |
![]()
|
|
Запросы по Флойду
Алгоритм Флойда
Дан неориентированный взвешенный граф с отрицательными весами, необходимо выдавать информацию о кратчайшем пути между 2 вершинами.
Входные данные
В первой строчке дано целое число n - количество вершин в графе. Дальше на вход подается матрица смежности, в которой -1 означает отсутствие ребра между вершинами. После матрицы идет число k - количество запросов, в следующих k строках содержится по 2 числа, a и b - вершины в запросе.
Выходные данные
Выведите k чисел - расстояние между парой чисел из запроса в порядке их ввода, если нельзя добраться из вершины a в вершину b, следует вывести Imp. Каждое число выводится в отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 3 -1
3 0 4
-1 4 0
3
1 3
3 2
1 2
|
7
4
3 |
| |
![]()
|
|
Самый короткий путь
Алгоритм Флойда
Дан ориентированный полный граф, рёбрам которого приписаны некоторые веса (длины). Веса могут быть и положительные, и отрицательные, и нулевые. Нас интересует минимум длин всех возможных путей между всеми парами различных вершин этого графа. Нужно будет выяснить, существует ли этот минимум, и, если существует, вычислить его. (Минимума не существует в том случае, если в графе можно найти путь отрицательной длины, сколь угодно большой по модулю, стремящийся к бесконечности).
Входные данные
В первой строке задано число вершин N≤50. Далее идёт матрица смежности графа, то есть N строк, в каждой из которых записано N чисел. j-ое число в i-ой строке матрицы смежности задает длину ребра, ведущего из i-й вершину в j-ую. Длины могут принимать любые значения от -1000000 до 1000000. Гарантируется, что на главной диагонали матрицы стоят нули.
Выходные данные
Выведите одно число – искомый минимум. Если его не существует, выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 42 18468
6335 0 26501
19170 15725 0
|
42 |
| 2 |
3
0 -7 3
-2 0 10
2 215 0
|
-1 |
| |
![]()
|
|
Отрицательный цикл
Алгоритм Флойда
Дан ориентированный граф. Определить, есть ли в нем цикл отрицательного веса.
Входные данные
В первой строке содержится число N (1 <= N <= 100) – количество вершин графа. В следующих N строках находится по N чисел – матрица смежности графа. Веса ребер по модулю меньше 100000. Если ребра нет, соответствующее значение равно 100000.
Выходные данные
В первой строке выведите "YES", если цикл существует, или "NO", в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
100000 100000 -51
100 100000 100000
100000 -50 100000
|
YES |
| |
![]()
|
|
Маршрут кладоискателя
Алгоритм Флойда
Обход в ширину
Вася из задачи A по-прежнему занят поиском кладов. Более того, у него появились последователи. Один из таких последователей попросил Васю помочь в своих поисках. Так, по карте сокровищ Васю просят восстановить кратчайший путь до клада. Конфигурация лабиринта совпадает с конфигурацией, описанной в задаче A (поле \(N \times M (1 \le N, M \le 100, N \times M \le 100))\), в одной клетке которого находится клад, в K
клетках находятся входы в лабиринт).
Требуется вывести искомый путь.
Формат входных данных
Первая строка содержит 2 числа N<=100 и M<=100, задающие размеры лабиринта. Далее следует описание лабиринта: N
строк по M символов в каждой. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с сокровищем (такая клетка в лабиринте ровно одна).
В (N+2)-й строке находится число \(K (1 \le K \le N \times M)\) - количество входов в лабиринт. Далее в K строках содержатся координаты входов. Так, в i-й строке содержатся числа \(x_i\) и \(y_i\), означающие, что i-й вход расположен в \(x_i\)-й строке и в \(y_i\)-м столбце \((1 \le x_i \le N, 1\le y_i \le M)\). Гарантируется, что координаты входов попарно различны, и то, что все входы расположены в пустых клетках. Ни один из входов не находится в клетке с сокровищем.
Формат выходных данных
В первой строке вывести одно число - длину кратчайшего маршрута. В следующих строках необходимо вывести кратчайший маршрут. Каждую клетку маршрута (включая начальную и конечную) вывести на отдельной строке в формате \(x_i\) \(y_i\), где \(x_i\) - строка клетки, а \(y_i\) - столбец клетки.
Если существует несколько путей минимальной длины, выведите любой. Если до сокровища невозможно добраться, в единственной строке выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5 |
4
1 1
2 1
2 2
3 2
3 3 |
| 2 |
3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
|
-1 |
| |
![]()
|
|
Рейсы во времени
Алгоритм Флойда
Между \(N\) населенными пунктами совершаются пассажирские рейсы на машинах времени.
В момент времени 0 вы находитесь в пункте \(A\). Вам дано расписание рейсов. Требуется оказаться в пункте \(B\) как можно раньше (то есть в наименьший возможный момент времени).
При этом разрешается делать пересадки с одного рейса на другой. Если вы прибываете в некоторый пункт в момент времени \(T\), то вы можете уехать из него любым рейсом, который отправляется из этого пункта в момент времени \(T\) или позднее (но не раньше).
Формат входных данных
Первая строка содержит число \(N\) — количество населенных пунктов (\(1 \le N \le 1000\)). Вторая строка содержит два числа \(A\) и \(B\) — номера начального и конечного пунктов. Третья строка содержит число \(K\) — количество рейсов (\(0 \le K \le 1000\)). Следующие \(K\) строк содержит описания рейсов, по одному на строке. Каждое описание представляет собой четверку целых чисел. Первое число каждой четверки задает номер пункта отправления, второе — время отправления, третье — пункт назначения, четвертое — время прибытия. Номера пунктов — натуральные числа из диапазона от 1 до \(N\). Пункт назначения и пункт отправления могут совпадать. Время измеряется в некоторых абсолютных единицах и задается целым числом, по модулю не превышающим \(10^9\). Поскольку рейсы совершаются на машинах времени, то время прибытия может быть как больше времени отправления, так и меньше, или равным ему.
Гарантируется, что входные данные таковы, что добраться из пункта \(A\) в пункт \(B\) всегда можно.
Формат выходных данных
Выведите минимальное время, когда вы сможете оказаться в пункте \(B\).
| |
![]()
|
|
Юный поджигатель
Алгоритм Флойда
Способы задания графа
На клеточном поле введена система координат так, что центр координат находится в точке пересечения линий сетки и оси направлены вдоль линий сетки.
На этом поле выложили связную фигуру, состоящую из спичек. Использовались спички двух типов:
- Спички длины 1 выкладывались по сторонам клеток.
- Спички длины выкладывались по диагоналям клеток.
Ребенок хочет сжечь фигуру. При этом он может поджечь ее в одной точке, имеющей целочисленные координаты (например, в точке A на рисунке поджигать фигуру нельзя, а в точках B и C — можно).
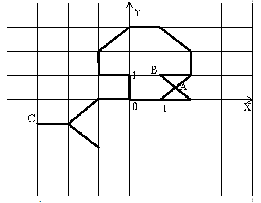
Известно, что огонь распространяется вдоль спички равномерно (но по каждой спичке — со своей скоростью). Спичка может гореть в нескольких местах (например, когда она загорается с двух концов; или когда в середине диагональной спички огонь перекидывается с одной спички на другую — огонь расползается по вновь подожженной спичке в обе стороны).
Напишите программу, которая определит, в какой точке нужно поджечь фигуру, чтобы она сгорела за минимальное время.
Входные данные
Во входном файле записано сначала число N — количество спичек (1<N<40). Затем идет N пятерок чисел вида X1, Y1, X2, Y2, T, задающих координаты концов спички и время ее сгорания при условии, что она будет подожжена с одного конца (гарантируется, что каждая спичка имеет длину 1 или , все спички образуют связную фигуру, и положение никаких двух спичек не совпадает). Все координаты — целые числа, по модулю не превышающие 200, время сгорания — натуральное число, не превышающее 107.
Выходные данные
Выведите координаты целочисленной точки, в которой нужно поджечь фигуру, чтобы она сгорела за наименьшее время, а затем время, за которое в этом случае фигура сгорит. Время должно быть выведено с точностью не менее 2-х знаков после десятичной точки. Если решений несколько, выведите любое из них.
| |
![]()
|
|
Есть ли цикл? - Флойдом
Обход в глубину
Алгоритм Флойда
Дан ориентированный граф. Используя алгоритм Флойда определите, есть ли в заданном графе цикл.
Формат входных данных
В первой строке вводится число вершин N≤ 50. Далее в N строках следуют по N чисел, каждое из которых – 0 или 1. j-ое число в i-ой строке равно 1 тогда и только тогда, когда существует ребро, идущее из i-ой вершины в j-ую. Гарантируется, что на диагонали матрицы будут стоять нули.
Формат выходных данных
Выведите 0, если в заданном графе цикла нет, и 1, если он есть.
| |
![]()
|
|
Все кратчайшие маршруты
Алгоритм Флойда
кратчайшие пути
Учёный-ботаник получил карту дорог страны Лимония. Чтобы составить план исследования этой страны, ему требуется найти кратчайшие расстояния между каждой парой городов этой страны (можно ехать только по проложенным дорогам). Помогите учёному – напишите программу, которая решает эту задачу.
Входные данные
В первой строке вводится количество городов N ( 1 ≤ N ≤ 100 ). В следующих N строках записано по N чисел, разделённых пробелами – элементы весовой матрицы графа, который описывает схему дорог между городами: положительное число означает расстояние между городами, ноль говорит о том, что дороги нет.
Выходные данные
Программа должна вывести все кратчайшие маршруты между всеми городами в следующем формате:
(1->3): 1 2 3 (23)
Сначала выводятся номера начального и конечного города (в скобках), затем – последовательность номеров городов, составляющая оптимальный маршрут, затем (в скобках) длина этого маршрута. Если между какими-то городами нет дороги, нужно вывести число 0.
|
Ввод |
Вывод |
|
4
0 0 0 0
0 0 2 1
0 2 0 4
0 1 4 0
|
(1,2): 0
(1,3): 0
(1,4): 0
(2,3): 2 3 (2)
(2,4): 2 4 (1)
(3,4): 3 2 4 (3)
|
| |
![]()
|
|
33228
Алгоритм Флойда
кратчайшие пути
В одной из деревень Центрального района решили построить новую школу, но никак не могут выбрать, в какой именно. Решили сделать так: подсчитать для каждой деревни суммарное расстояние, которое будут проходить все школьники Центрального района, если школа будет построена в этой деревне, и выбрать место, для которого эта сумма будет минимальной. В распоряжении администрации есть карта дорог Центрального района. Напишите программу, которая поможет выбрать место для школы. Если какой-то населенный пункт не имеет связи с другим населенным пунктом, где предполагается разместить школу, считайте, что доставка каждого ученика вертолётом "стоит" 10000 единиц расстояния.
Входные данные
В первой строке вводится количество деревень N ( 1 ≤ N ≤ 100 ). В следующих N строках записано по N чисел, разделённых пробелами – элементы весовой матрицы графа, который описывает схему дорог: положительное число означает расстояние между деревнями, ноль говорит о том, что дороги нет. В последней строке вводится N чисел - количество школьников в каждой деревне.
Выходные данные
Программа должна вывести два числа: сначала номер деревни, где нужно построить школу, а затем (через пробел) – общее расстояние, которое будут проходить все школьники Центрального района, если школа будет построена в этой деревне.
|
Ввод |
Вывод |
|
4
0 11 8 4
11 0 2 5
8 2 0 13
4 5 13 0
15 26 30 12
|
2 255 |
| |
![]()
|
|
Pink Floyd
Алгоритм Флойда
кратчайшие пути
графы
Группа Pink Floyd собирается дать новый концертный тур по всему миру. По предыдущему опыту группа знает, что солист Роджер Уотерс постоянно нервничает при перелетах. На некоторых маршрутах он теряет вес от волнения, а на других - много ест и набирает вес.
Известно, что чем больше весит Роджер, тем лучше выступает группа, поэтому требуется спланировать перелеты так, чтобы вес Роджера на каждом концерте был максимально возможным. Группа должна посещать города в том же порядке, в котором она дает концерты. При этом между концертами группа может посещать промежуточные города.
Входные данные
Первая строка входного файла содержит три натуральных числа n, m и k - количество городов в мире, количество рейсов и количество концертов, которые должна дать группа соответственно (n≤100, m≤104, 2≤k≤104). Города пронумерованы числами от 1 до n. Следующие m строк содержат описание рейсов, по одному на строке. Рейс номер i описывается тремя числами bi, ei и wi - номер начального и конечного города рейса и предполагаемое изменение веса Роджера в миллиграммах (1≤bi,ei≤n, −105≤wi≤105). Последняя строка содержит числа a1, a2, ..., ak - номера городов, в которых проводятся концерты. В начале концертного тура группа находится в городе a1.Гарантируется, что группа может дать все концерты.
Выходные данные
Первая строка выходного файла должна содержать число s - количество рейсов, которые должна сделать группа. Вторая строка должна содержать s чисел - номера используемых рейсов. Если существует такая последовательность маршрутов между концертами, что Роджер будет набирать вес неограниченно, то первая строка выходного файла должна содержать строку “infinitely kind”.
|
Ввод |
Вывод |
|
4 8 5
1 2 -2
2 3 3
3 4 -5
4 1 3
1 3 2
3 1 -2
3 2 -3
2 4 -10
1 3 1 2 4
|
6
5 6 5 7 2 3
|
|
4 8 5
1 2 -2
2 3 3
3 4 -5
4 1 3
1 3 2
3 1 -2
3 2 -3
2 4 10
1 3 1 2 4
|
infinitely kind |
| |
![]()
|
|
Столовая
Алгоритм Флойда
кратчайшие пути
Сегодня у студентов праздник! В одном из новых зданий университета решили открыть столовую. Для этих целей требуется выбрать одно из зданий, в котором и будет располагаться столовая. Чтобы студенты как можно меньше отвлекались от учёбы, было решено выбрать такое здание, чтобы максимальное расстояние от него до всех остальных зданий было как можно меньше.
Помогите найти такое здание!
Входные данные
В первой строке находятся два числе N и M - количество зданий и количество дорог, соединяющих здания (1<=N<=100, 0 <=M<=(N(N−1))/2. Далее в M строках расположены описания дорог: 3 целых числа si, ei, li - здания, в которых начинается и заканчивается дорога и длина дороги соответственно (1<=si, ei<=N, 0<=li,=100, дороги двунаправленные).
Выходные данные
Необходимо вывести одно число - номер искомого здания. Если есть несколько зданий удовлетворяющих поставленным критериям, выберите среди них здание с наименьшим номером.
|
Ввод |
Вывод |
|
3 2
1 2 1
2 3 2
|
2 |
|
3 1
1 2 10
|
1 |
| |
![]()
|
|
Два профессора
Алгоритм Флойда
Профессор Флойд и профессор Дейкстра ненавидят друг друга. После переезда университета во вновь отстроенный университетский городок они потребовали себе кабинеты в зданиях, максимально удалённых друг от друга. Вам поручено найти расстояние между двумя такими зданиями.
Иными словами, требуется найти два здания, кратчайший путь между которыми наибольший среди всех пар зданий, и вывести длину этого пути. Так как профессорам иногда все же нужно встречаться, путь между выбранными зданиями должен существовать.
Входные данные
В первой строке находятся два числа N и M - количество зданий и количество дорог, соединяющих здания (1<=N<=100, 0<=M<= (N(N−1))/2. Далее в M строках расположены описания дорог: 3 целых числа si, ei, li - здания, в которых начинается и заканчивается дорога и длина дороги соответственно (1<=si, ei<=N, 0<=li<=100, дороги двунаправленные).
Выходные данные
Необходимо вывести одно число - искомое расстояние.
|
Ввод |
Вывод |
|
3 2
1 2 1
2 3 2
|
3 |
|
3 0 |
0 |
| |
![]()
|
|
Флойд: Начало №2
Алгоритм Флойда
Полный ориентированный взвешенный граф задан матрицей смежности. Постройте матрицу кратчайших путей между его вершинами. Гарантируется, что в графе нет циклов отрицательного веса.
Входные данные
В первой строке вводится единственное число N (1 <= N <= 100) – количество вершин графа. В следующих N строках по N чисел задается матрица смежности графа (j-ое число в i-ой строке соответствует весу ребра из вершины i в вершину j). Все числа по модулю не превышают 100. На главной диагонали матрицы – всегда нули.
Выходные данные
Выведите N строк по N чисел – матрицу кратчайших расстояний между парами вершин. j-ое число в i-ой строке должно быть равно весу кратчайшего пути из вершины i в вершину j.
|
Ввод |
Вывод |
|
4
0 5 9 100
100 0 2 8
100 100 0 7
4 100 100 0
|
0 5 7 13
12 0 2 8
11 16 0 7
4 9 11 0
|
| |
![]()
|
|
Флойд №2
Алгоритм Флойда
кратчайшие пути
Дан ориентированный взвешенный граф. Вам необходимо найти пару вершин, кратчайшее расстояние от одной из которых до другой максимально среди всех пар вершин.
Входные данные
В первой строке вводится единственное число N (1 <= N <= 100) – количество вершин графа. В следующих N строках по N чисел задается матрица смежности графа, где -1 означает отсутствие ребра между вершинами, а любое неотрицательное число – присутствие ребра данного веса. На главной диагонали матрицы – всегда нули.
Выходные данные
Выведите искомое максимальное кратчайшее расстояние.
|
Ввод |
Вывод |
|
6
0 6 8 -1 -1 -1
5 0 5 -1 -1 -1
1 7 0 -1 -1 -1
-1 -1 -1 0 6 -1
-1 -1 -1 -1 0 3
-1 -1 -1 2 -1 0
|
9 |
| |
![]()
|
|
Флойд
Алгоритм Флойда
Дан ориентированный граф, рёбрам которого приписаны некоторые неотрицательные веса (длины). Найти длину кратчайшего пути из вершины s в вершину t.
Входные данные
В первой строке заданы три числа: число вершин в графе N ≤50, номера вершин s и t. Далее идёт матрица смежности графа, то есть N строк, в каждой из которых записано N чисел. j-ое число в i-ой строке матрицы смежности задает длину ребра, ведущего из i-й вершину в j-ую. Длины могут принимать любые значения от 0 до 1000000, число -1 означает отсутствие соответствующего ребра. Гарантируется, что на главной диагонали матрицы стоят нули.
Выходные данные
Выведите одно число – минимальную длину пути. Если пути не существует, выведите -1.
|
Ввод |
Вывод |
|
3 1 2
0 -1 3
7 0 1
2 215 0
|
218 |
| |
![]()
|