Плюсануть
Поделиться
Класснуть
Запинить


Олимпиадный тренинг

Вы можете самостоятельно решать эти задачи столько раз, сколько вам это понадобится.
   

Минимум на отрезке неизменяемого массива

Разреженные таблицы (sparse table)

Вам дан массив A [1…N]. Требуется выполнить M операций вычисления минимального элемента на отрезке с L по R.

Входные данные
Первая строка содержит число N (\(1 <= N <= 100000\)) – размер массива. Во второй строке записаны N чисел – элементы массива. Третья строка содержит число M (\(1 <= M <= 100000\)) – количество запросов минимума. Следующие M строк содержат пары чисел L и R (\(L <= R <= N\)), описывающие отрезки.

Выходные данные
Для каждого запроса выведите значение минимума на отрезке через пробел.

 

Примеры
№ Входные данные Выходные данные
1 5
3 1 8 7 9
2
1 3
3 5		 1 7

Олег Евгеньевич и новая Counter-Strike

Разреженные таблицы (sparse table)

Недавно вышла новая игра Counter-Strike 2. В 5-м классе учится N человек, и все они хотят поиграть в эту игру. На уроке физкультуры всех учеников построили в шеренгу. У физрука Олега Евгеньевича сегодня смешанное настроение: он решил разрешить ученикам поиграть в CS2 вместо физических занятий, но играть они будут только по определенным правилам. 

Олег Евгеньевич будет разрешать играть всем ученикам, номер в шеренге которых лежит в отрезке \([L;R]\). Олег Евгеньевич узнал, что родители детей разрешают играть им в компьютер только ti минут. Но ученики очень любят компьютерные игры, поэтому каждый будет играть ровно ti минут, при этом играть никто не отказывается. 

Игра происходит следующим образом: выбирается время матча такое, что каждый ученик должен сыграть строго целое число матчей, при этом количество сыгранных матчей у каждого ученика может различаться и время матча должно быть максимально возможным. 

Например, играют 2 игрока. Если у играющего 1 время \(t_1 = 12\), а у играющего 2 время \(t_2 = 8\), то максимально возможное время матча 4 минуты. 1 играющий сможет сыграть 3 матча по 4 минуты, а 2 – 2 матча по 4 минуты. 

Олег Евгеньевич в последнее время усердно занимается математикой, поэтому он решил M раз посчитать максимальное время Q для играющих от L до R. Вам следует проверить Олега Евгеньевича. Для этого следует вывести YES, если он прав, иначе – NO.

Входные данные
Первая строка содержит число N (\(1 <= N <= 10000\)) – количество ребят. Во второй строке записаны N чисел – ti (\(1 <= t_i <= 1000\)), время, которое дают родители i-ому ребенку на игру. В третьей строке записано число M (\(1 <= M <= 10^8\)), количество запросов. Далее, в M строках идут 3 числа L, R, Q (время, которое посчитал Олег Евгеньевич).

Выходные данные
Выведите для каждого запроса YES, если Олег Евгеньевич правильно посчитал, иначе – NO.

 

Примеры
№ Входные данные Выходные данные
1 3
8 5 6
4
1 2 2
1 3 1
2 3 1
1 3 2		 NO
YES
YES
NO

Воздушные потоки

Деревья Наименьший общий предок Разреженные таблицы (sparse table) Структуры данных Префиксные суммы(минимумы, ...)

Колобок ушёл от бабушки и поехал путешествовать. Неожиданно для себя он забрёл в страну Ивэнлэнд. Первые трудности встали на его пути: Колобка и вход в страну отделял огромный ров с водой, которая, как известно, не очень хорошо влияет на нашего героя. К счастью, повсюду рас- положены воздушные потоки, которые могли поднимать того, кто на них встает, на определённую высоту. Страна не просто так названа Ивэнлэнд, поэтому все высоты, на которые могут поднять героя воздушные потоки — это чётные числа.

Представим воздушные потоки как массив h[1..n] из n натуральных чисел — высот потоков. Для каждого 1 ≤ i ≤ n посчитаем G[i] — индекс ближайшего элемента слева, строго большего h[i]. Более формально, g[i] = max{j | j < i и h[j] > h[i]}. Если i = 1 или до h[i] нет ни одного элемента больше него, то G[i] считается равным 0.

Колобок считает, что оптимальность расположения воздушных потоков определяется суммой


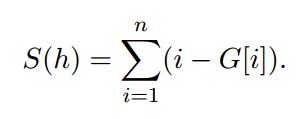
Чем меньше сумма, тем расположение оптимальнее. Всё, что может сейчас сделать Колобок — это увеличить высоту одного из воздушных потоков не более чем на m. После этого действия высота потока должна остаться целым числом, но может, если необходимо, стать и нечётной.

Помогите Колобку сделать оптимальное изменение, которое позволит добиться, чтобы сумма S(h), описанная выше, после проделанного действия была минимальна.

Формат входного файла
В первой строке входного файла даны числа n, m (1 ≤ n ≤ 105 , 1 ≤ m ≤ 109 ) — количество воздушных потоков и максимальное значение, на которое можно увеличить высоту одного из них. Во второй строке даны высоты воздушных потоков h[i] (1 ≤ h[i] ≤ 109 ). Гарантируется, что все высоты — чётные числа.

Формат выходного файла
В единственной строке выходного файла выведите одно целое число — минимальную искомую сумму.
 

Ввод Вывод
3 100
4 2 6		 4
3 2
4 2 6		 5
3 10
2 2 2		 4

Путь в никуда

Деревья Деревья Структуры данных Разреженные таблицы (sparse table) Бинарный поиск Префиксные суммы(минимумы, ...)

Колобку снится странный сон.
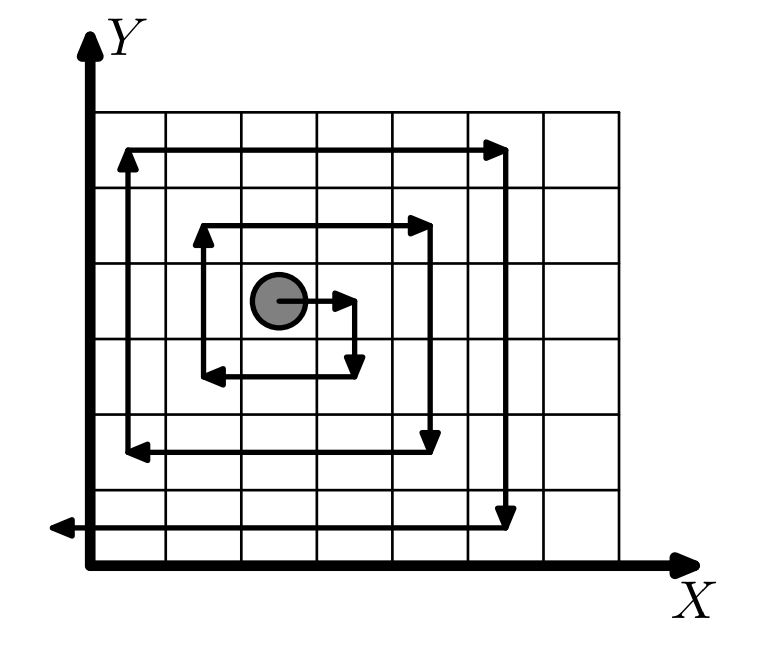
В нём Колобок находится на клетчатом поле размера n × m в клетке с координатами (x, y).
Изначально Колобок смотрит вдоль положительного направления оси X. Затем он начинает идти по полю со следующей закономерностью:
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на четыре клетки вперед. Повернуть на 90o вправо.
• И так далее...

Движение продолжается до тех пор, пока Колобок не выйдет за границы поля. После этого Колобок просыпается.

Утром Колобок решил проанализировать свой сон. Он догадался, что в каждой клетке он был максимум один раз, но никак не может вспомнить, сколько клеток он посетил. Колобок просит вас написать программу, которая посчитает количество посещённых им клеток.




Формат входного файла
В первой строке входного файла находятся два натуральных числа n, m (1 ≤ n, m ≤ 109 ) — размеры доски вдоль оси X и оси Y соответственно. Во второй строке находятся два натуральных числа x, y (1 ≤ x ≤ n; 1 ≤ y ≤ m) — координаты стартовой позиции колобка.

Формат выходного файла
В выходной файл выведите одно число — количество клеток, посещенных Колобком во сне.
 

Вывод Ввод
7 6
3 4		 36
2 2
1 1		 2
2 2
1 2		 4

Комментарий
На рисунке наглядно показан первый пример.
 

Берляндия атакует

Наименьший общий предок Дерево отрезков, RSQ, RMQ Разреженные таблицы (sparse table)

В этой задаче Вам вновь придется помочь Берляндии. Эта страна состоит из n городов, некоторые пары из которых соединены двусторонними дорогами, каждая дорога характеризуется своей длиной. Все города пронумерованы числами от 1 до n, столица имеет номер 1. Время от време ни Президент объезжает страну, посещая города страны. Целью каждой поездки является один из городов, к которому он едет из столицы вдоль дорог одним из кратчайших путей.

В далекие времена (когда задачи на алгоритм Дейкстры вызывали сложность) специальное ведомство составила такой набор дорог T, вдоль которого можно было проехать из столицы в любой город, причем единственным образом. Разумеется, путь по дорогам из набора T из столицы в каждый город являлся кратчайшим. Особо умные жители страны попросту называли этот набор дорог "деревом кратчайших путей". Известно, что Президент пользовался дорогами из T во время своих поездок. За прошедшие годы этот набор перестал быть секретным, и, поэтому, стал объектом повышенного внимания берляндских экстремистов. У специального ведомства новое задание. Для каждого города кроме столицы необходимо вычислить кратчайшее расстояние до него, при условии, что та дорога по которой Президент должен был закончить свой путь в этот город является атакованной и проезжать по ней нельзя.

Входные данные
В первой строке входного файла записана пара целых чисел n и m (2 ≤ n≤ 4000; n−1 ≤ m ≤100000), где n — количество городов в стране, а m— количество дорог в этой стране. Далее в m строках содержатся описания дорог, по одной дороге в строке. Каждая дорога задается четверкой целых чисел aj, bj, lj, tj , где aj, bj это номера городов, соединяемых дорогой (1 ≤ aj,bj ≤ n; aj≠bj), lj — ее длина (1 ≤ lj≤ 105), а tj равно 1 если дорога принадлежит дереву кратчайших путей и 0 в противном случае.

Гарантируется, что набор T удовлетворяет описанным выше свойствам. Между парой городов может быть более одной дороги. Все дороги двусторонние.

Выходные данные
Выведите n−1 число в строку через пробелы. i-ое число должно быть равно либо длине кратчайшго пути из столицы в город i+1, при условии, что по той дороге из T, которой Президент заканчивал свой путь в этот город, передвигаться нельзя, либо -1, если добраться до города i+1 вообще невозможно.
Hallowen